Analysis of Sampling-Based Planners

Thomas Cohn

RLG Short Talk - November 22, 2024
Probabilistic Roadmaps
Michigan Robotics 320, Lecture 15



Rapidly-Exploring Random Trees
Pathfinding with Rapidly-Exploring Random Tree, Knox
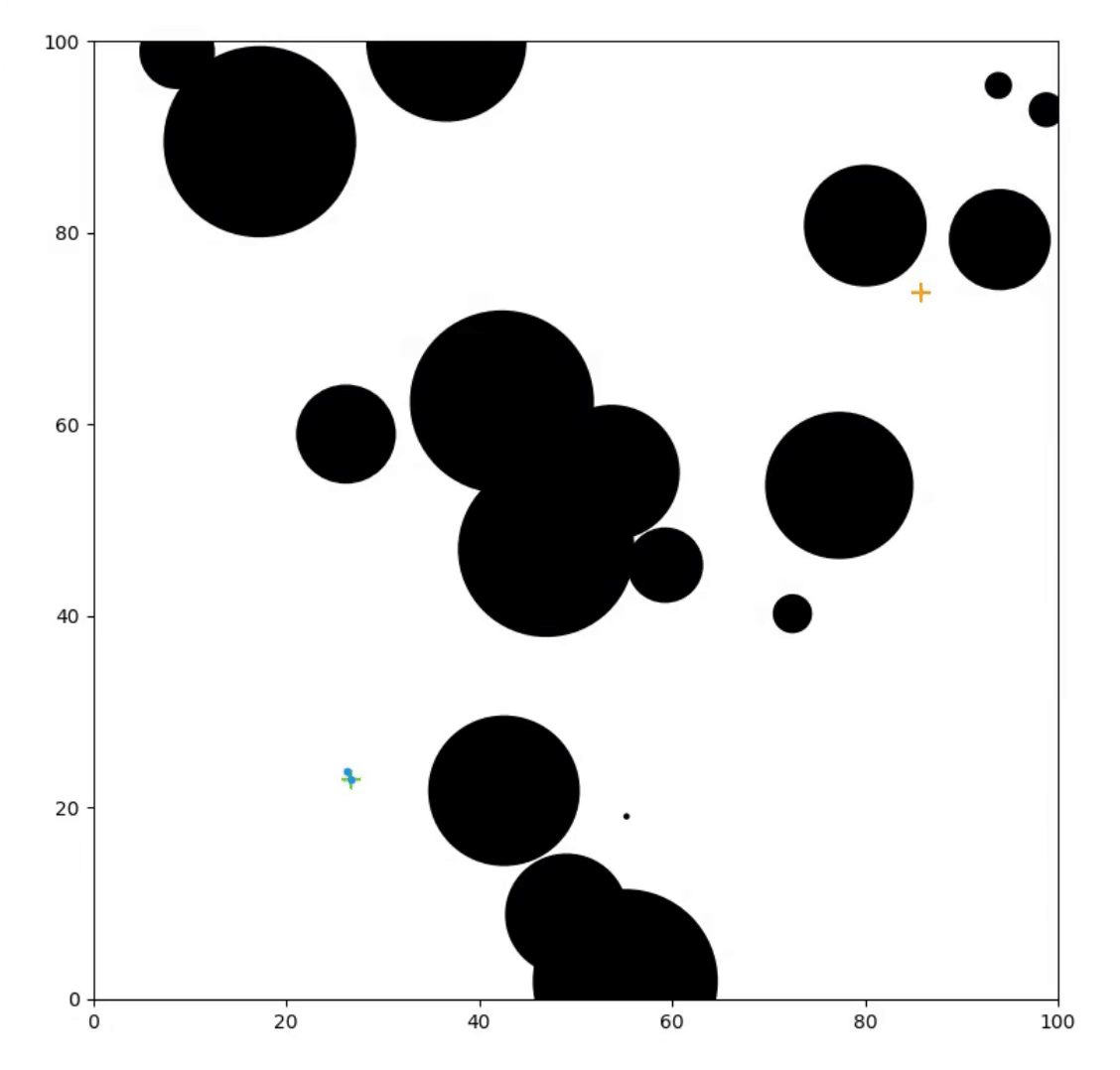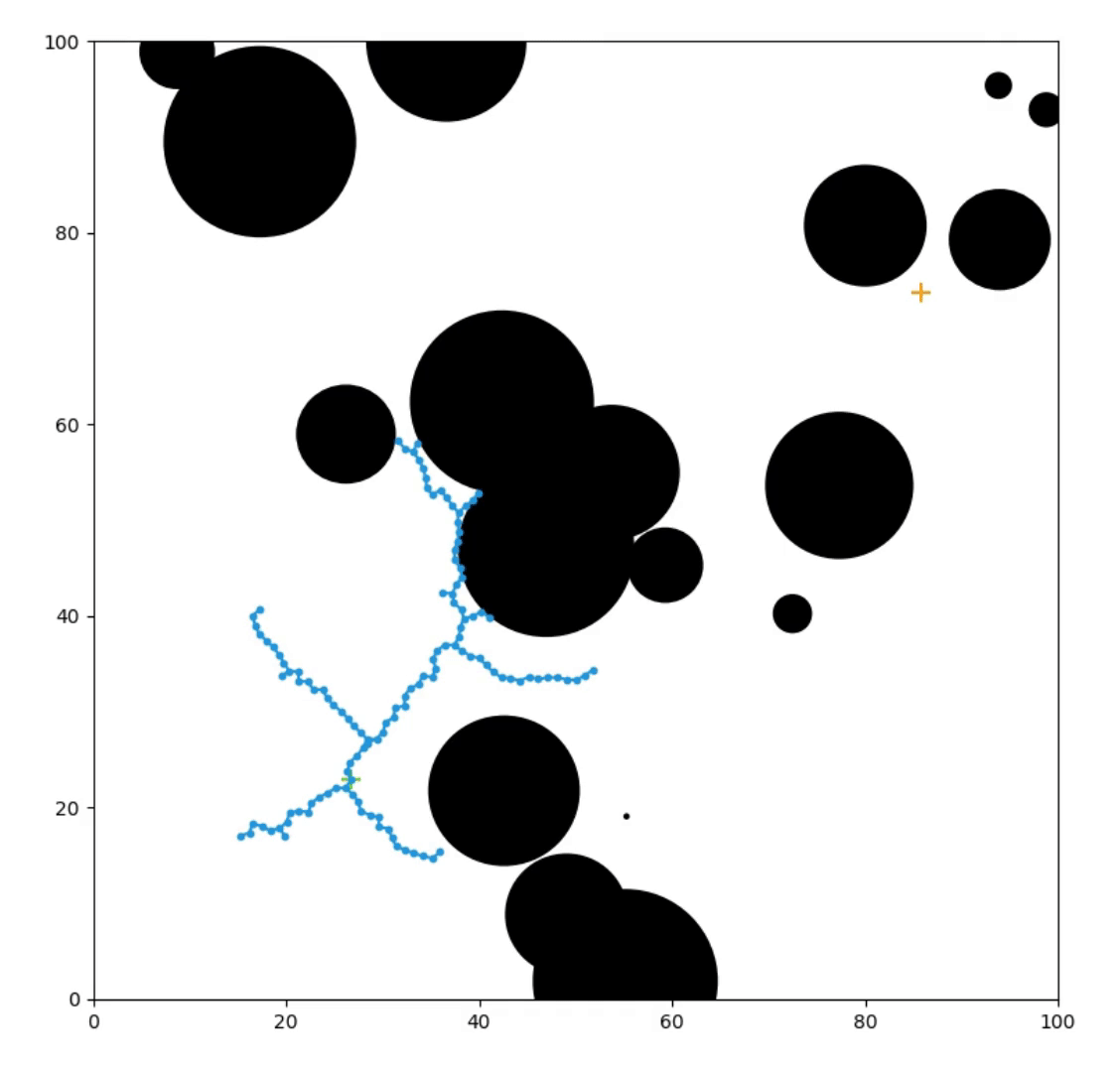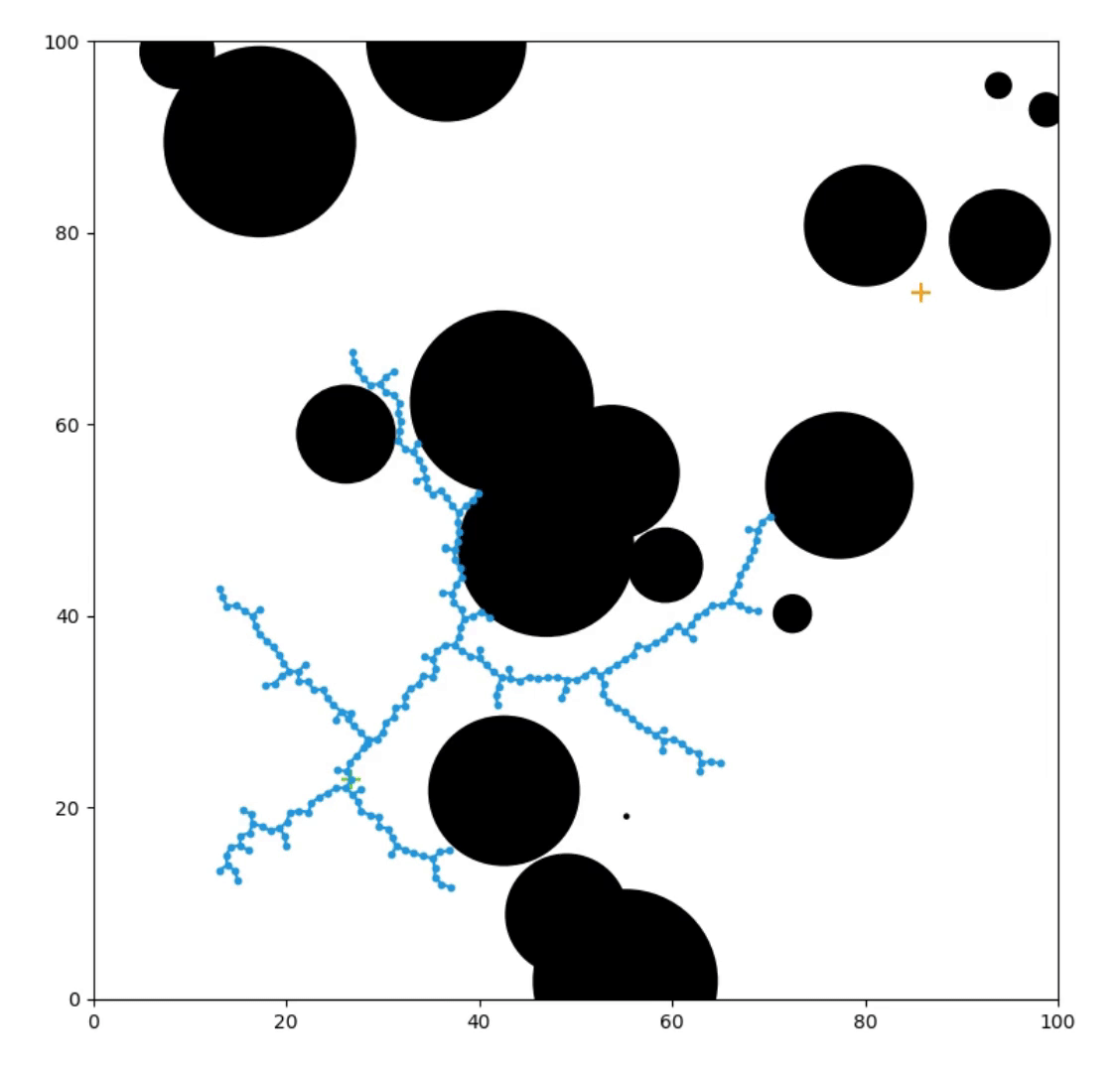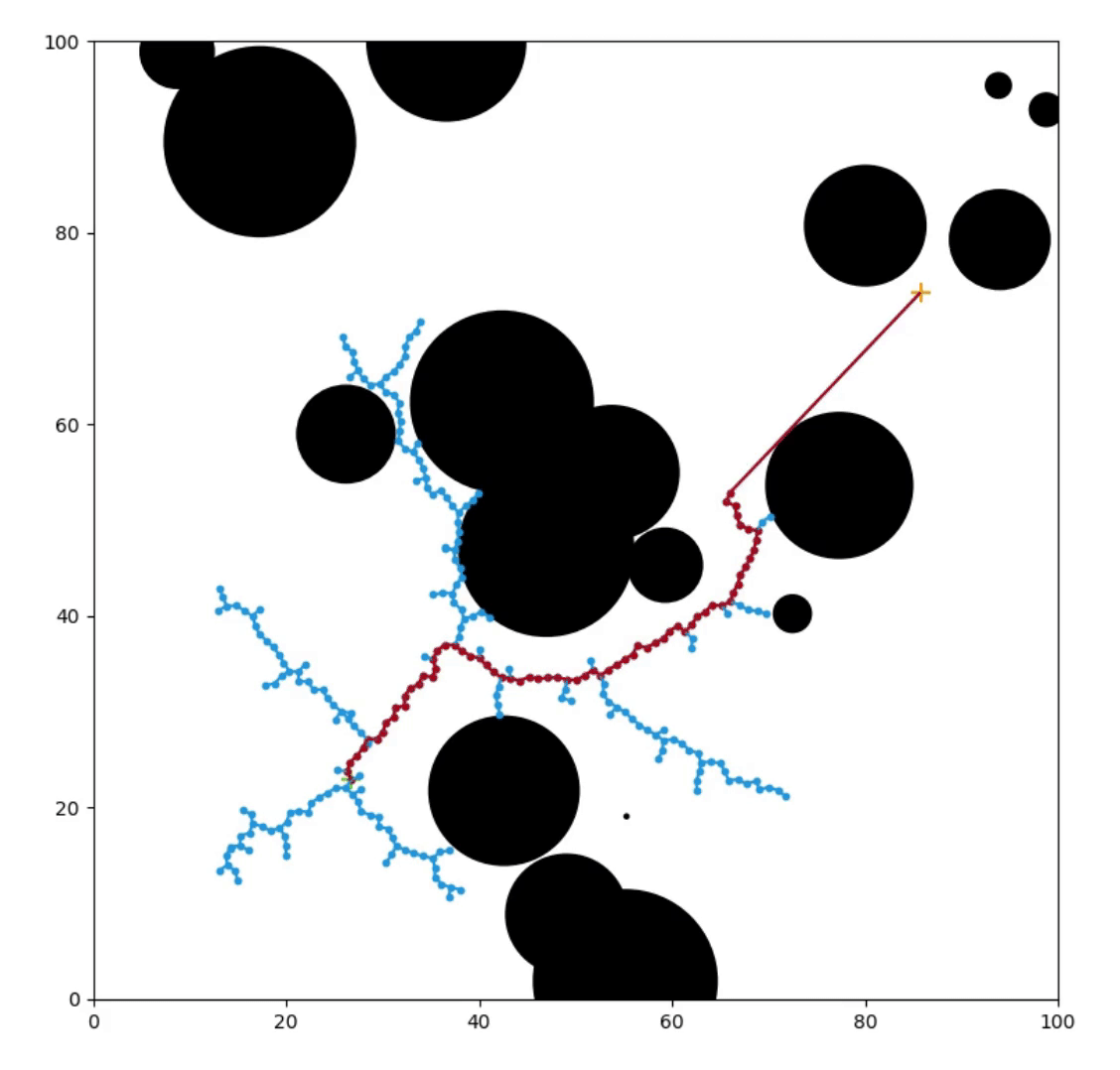

Things We Care About
- As the number of samples goes to infinity...
- Probabilistic Completeness (PC): If a path exists, the probability it hasn't been found goes to zero.
- Asymptotic Optimality (AO): The difference in cost of the current path and the optimal path goes to zero.
- Sample complexity bounds
- What is the probability we have found a path after a certain number of iterations?
- What is the expected number of iterations we need to find a path?
Properties of Space
- Configuration space \(\mathcal C\) and collision-free space \(\mathcal C_\mathrm{free}\subseteq\mathcal C\)
- Reachable set \(\mathcal R(x)\), for \(x\in\mathcal C_\mathrm{free}\)
- Set of all configurations that can be reached from \(x\)
- \(\ell\)-reachable set \(\mathcal R_\ell(x)\), for \(x\in\mathcal C_\mathrm{free}\)
- Set of all configurations that can be reached in \(\ell\) steps by a local planner
- Visible set \(\mathcal V(x)\), for \(x\in\mathcal C_\mathrm{free}\)
- Equivalent to 1-reachable set for a straight-line local planner.
- The volume of a set \(X\) is denoted \(\mu(X)\)
Setup for the RRT Algorithm
- Start configuration \(x_\mathrm{init}\in\mathcal C_\mathrm{free}\)
- Goal region \(X_\mathrm{goal}\subseteq\mathcal C_\mathrm{free}\)
- In practice, we can choose a small ball around a goal configuration \(x_\mathrm{goal}\in\mathcal C_\mathrm{free}\)
- \(\eta\) step size
- \(k\) iteration limit
The RRT Algorithm

Probabilistic completeness of RRT for geometric and kinodynamic planning with forward propagation, Kleinbort et. al.
Clearance
A path \(\gamma:[0,1]\to\mathcal C\) is \(\delta\)-clear if you can push a ball of radius \(\delta\) along the path without hitting an obstacle.
Note: defined for a specific path!
Klampt Documentation
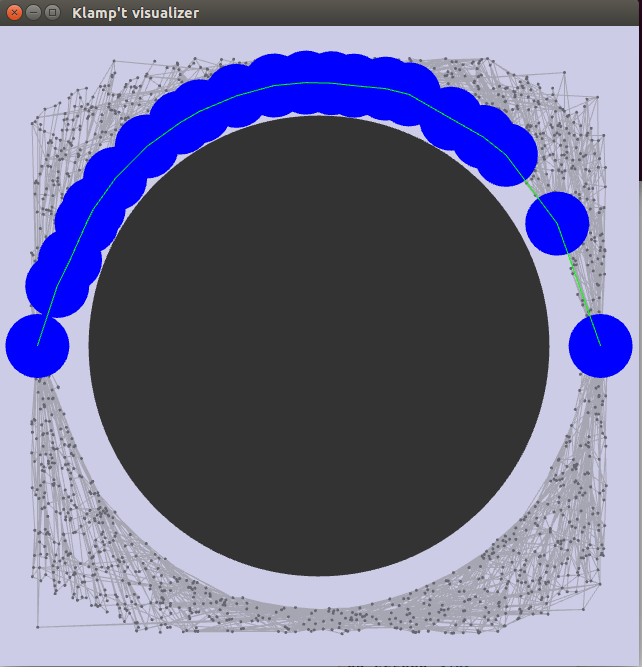
RRT is PC

RRT Sample Complexity
- Let \(p\) be the probability a sample is drawn from a ball
- Let \(m\) be the number of balls needed to cover the path
- Let \(k\) be the number of iterations
Then the probability RRT fails to reach the goal in k iterations is at most \[\frac{1}{(m-1)!}k^mme^{-pk}\]
What happens as clearance increases?
- \(p\) increases
- \(m\) decreases
The PRM Algorithm
Measure Theoretic Analysis of Probabilistic Path Planning, Ladd and Kavraki

PRM Sample Complexity
- Let \(L\) be the length of the path
- Let \(\epsilon\) be the clearance of the path
- Let \(H(n)\) be the \(n\)th Harmonic number
Then the expected number of samples needed for the PRM to find a path is at most \[\frac{H(\frac{2L}{\epsilon})\mu(\mathcal C_\mathrm{free})}{\mu(B_{\epsilon/2}(\cdot))}\]
What happens as clearance increases?
- \(H(\tfrac{2L}{\epsilon})\) decreases
- \(\mu(B_{\epsilon/2}(\cdot))\) increases
A Stronger Bound: Expansiveness
- Fix \(\alpha,\beta\in(0,1]\)
- Fix \(S\subseteq\mathcal C_\mathrm{free}\)
- The \(\beta\)-lookout of \(S\) is \[\{p\in S:\mu(\mathcal R_\ell(p)\setminus S)\ge\beta\mu(\mathcal R(S)\setminus S)\}\]
- A set \(S\) is \((\alpha,\beta)\)-expansive if for any connected \(S'\subseteq S\), \[\mu(\beta\mathrm{-lookout}(S'))\ge\alpha\mu(S')\]
- \(\mathcal C_\mathrm{free}\) is \((\alpha,\beta)\)-expansive if \(\forall p\in\mathcal C_\mathrm{free}\), \(\mathcal{R}(p)\) is \((\alpha,\beta)\)-expansive
- If \(\alpha'\le\alpha\) and \(\beta'\le\beta\), then \(\mathcal C_\mathrm{free}\) is also \(\alpha',\beta'\)-expansive.
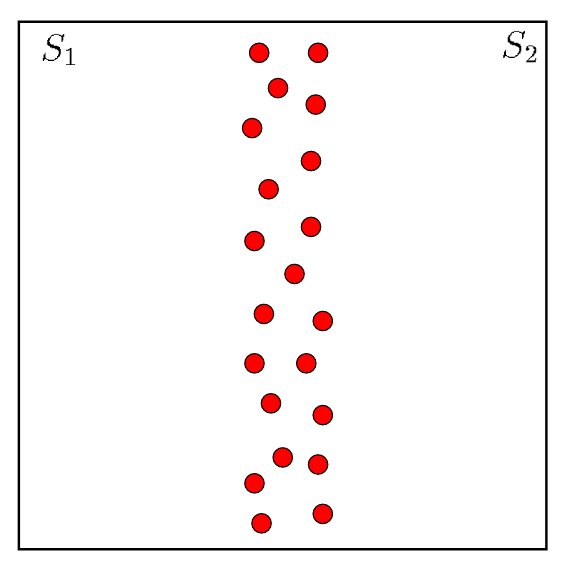
Expansiveness vs Clearance
The space on the right has low clearance by high expansiveness
Even though there are narrow passageways, it's still easy to cross the middle region
Randomized Single-Query Motion Planning in Expansive Spaces, Hsu
Further Definitions
- \(\mathcal C_\mathrm{free}\) is \(\epsilon\)-good, for \(\epsilon\in(0,1]\), if \(\forall p\in\mathcal C_\mathrm{free}\), \(\mu(\mathcal V(p))\ge\epsilon\mu(\mathcal C_\mathrm{free})\)
- Intuition: the visibility set of each point is at least an \(\epsilon\) fraction of the free space
- A set of points \(p_i\) in \(\mathcal C_\mathrm{free}\) provides adequate coverage if \[\mu\left(\mathcal C_\mathrm{free}\setminus\bigcup_{i}\mathcal V(p_i)\right)\le\frac{\epsilon}{2}\mu(\mathcal C_\mathrm{free})\]
- Intuition: the points not visible from any \(p_i\) are at most an \(\epsilon/2\) fraction of the free space
Sample Complexity of PRM
Theorem (Hsu): Suppose \(\mathcal C_\mathrm{free}\) is connected. Fix \(\gamma\in(0,1]\). If we randomly sample \(2n+2\) points, with \[n\ge 8\ln(8/\epsilon\alpha\gamma)/\epsilon\alpha+3/\beta,\] then with probability at least \(1-\gamma\), the resulting visibility graph is connected.
A note: the result is actually stated for possibly-disconnected spaces -- in that case, the subgraph corresponding to each connected component of \(\mathcal C_\mathrm{free}\) is connected.