Constrained Motion Planning and Analytic Inverse Kinematics
Thomas Cohn
CSCI 5551 Guest Lecture
4/22/2024
Constrained Bimanual Motion Planning




Images Generated by Microsoft Copilot
Outline
- Constrained Planning
- Analytic Inverse Kinematics
- Parametrizing the Constraint Manifold
- Planning with the Parametrization
Part 1
Constrained Planning
Configuration-Space Planning
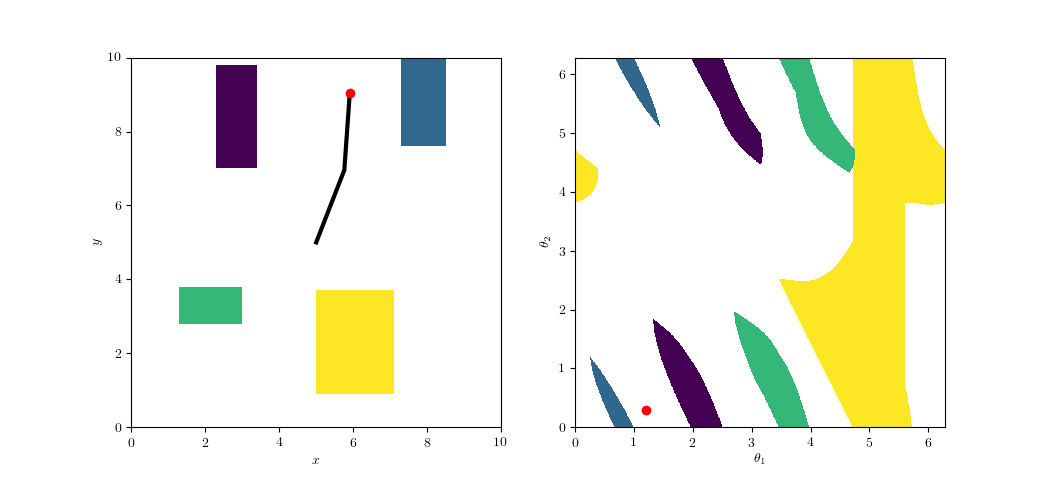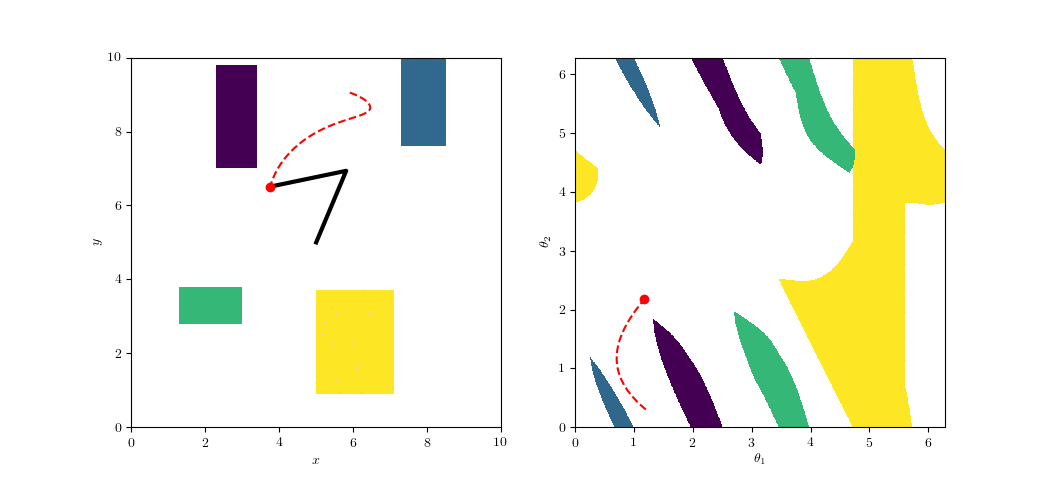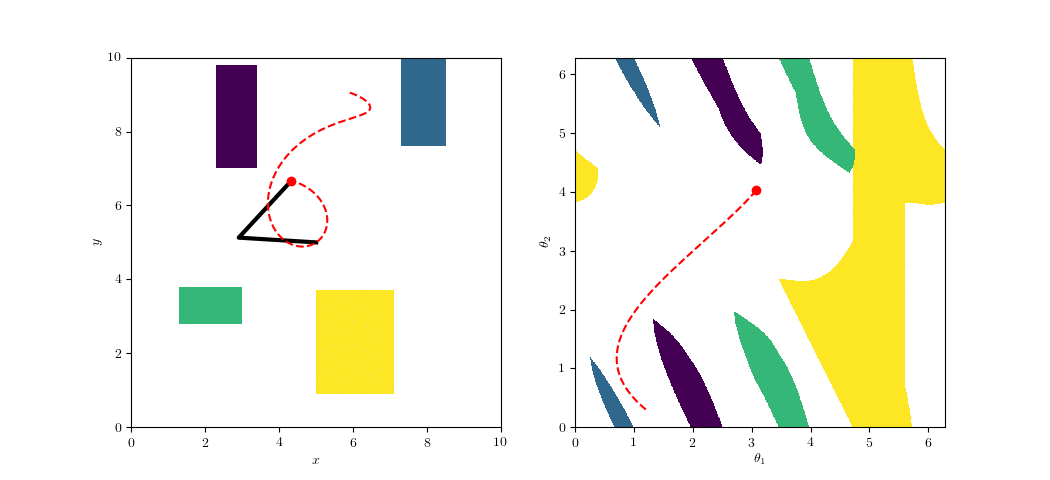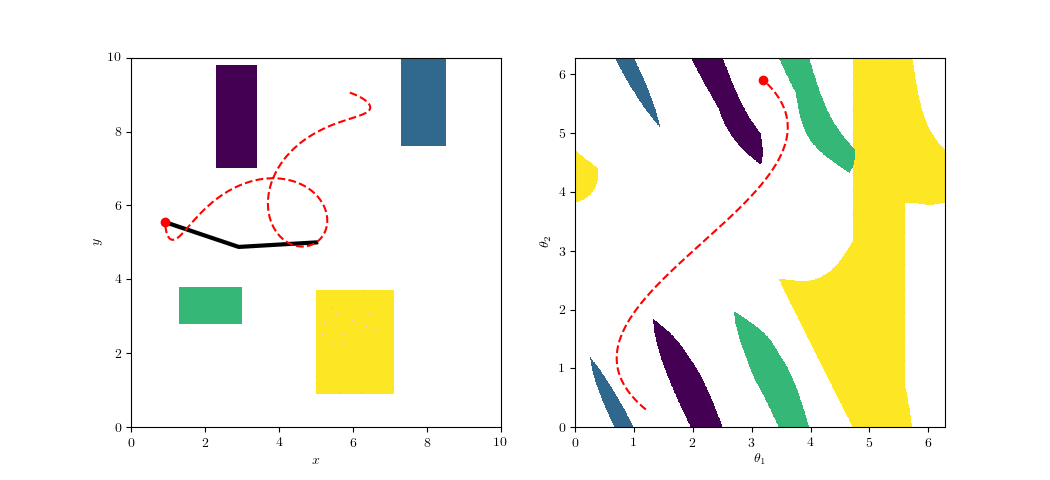
https://github.com/ethz-asl/amr_visualisations
An Illustrative Example
Learning the Metric of Task Constraint Manifolds for Constrained Motion Planning, Zha et. al.

How Can We Draw Samples?
Sampling-Based Methods for Motion Planning with Constraints, Kingston et. al.
Numerical Projection
Linear Approximation
Numerical Projection

Newton's Method in Optimization, Wikipedia
Gradient Descent (Green)
Newton's Method (Red)
Numerical Continuation
Multiple Parameter Continuation: Computing Implicitly Defined k-manifolds, Henderson et. al.
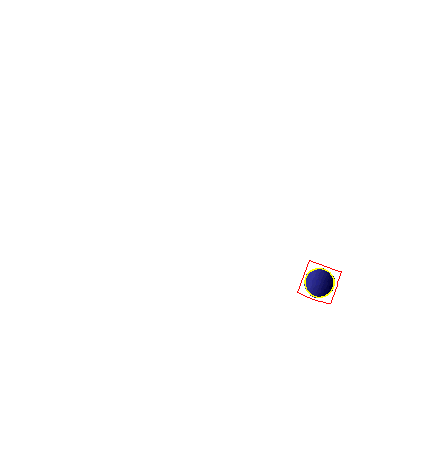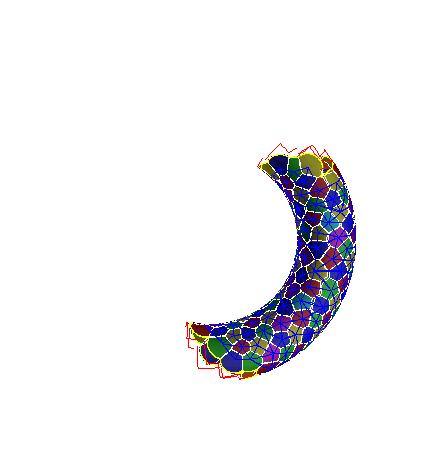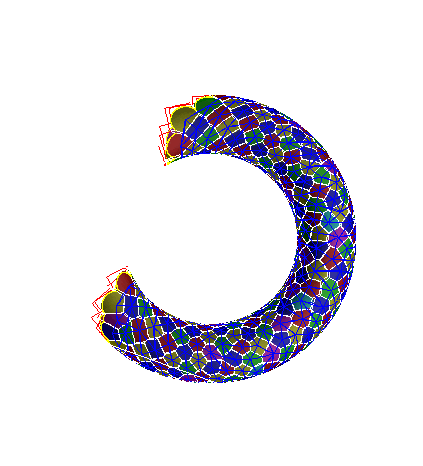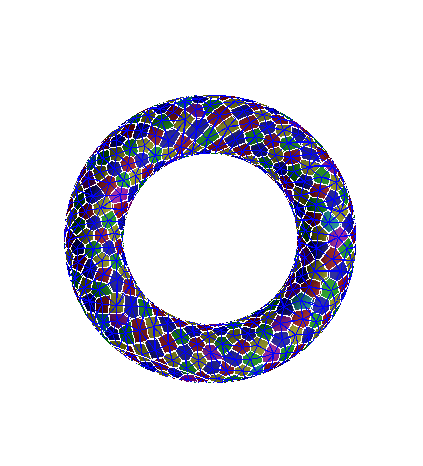
Numerical Continuation
Path Planning Under Kinematic Constraints by Rapidly Exploring Manifolds, Jaillet et. al.

Compliance (or Great Control)
Noninteracting Constrained Motion Planning and Control for Robot Manipulators, Bonilla et. al.

Part 2
Analytic Inverse Kinematics

Inverse Kinematics
https://thewanderingtech.blogspot.com/2009/06/educational-flash-application-on.html


Global Inverse Kinematics via
Mixed-Integer Convex Optimization, Dai et. al.
https://www.youtube.com/watch?v=c87OyAZDS54
Analytic Inverse Kinematics
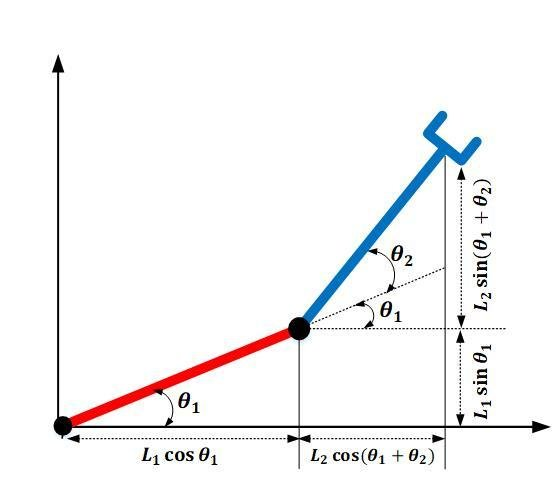
Robot Arm Free Cartesian Space Analysis for Heuristic Path Planning Enhancement, Raheem et. al.
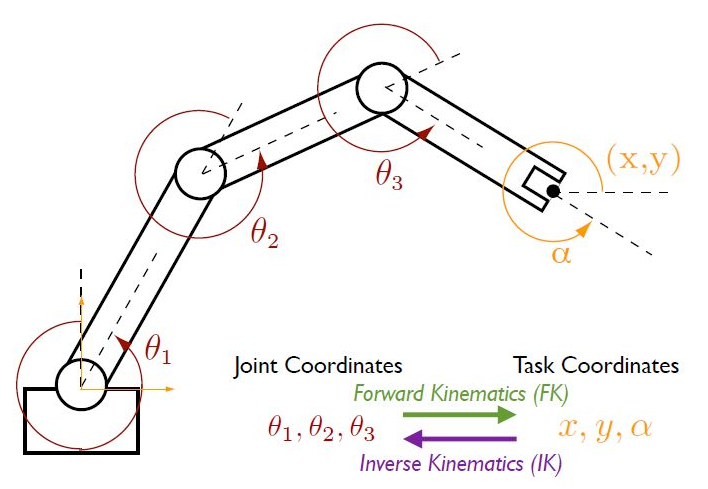
https://disigns.wordpress.com/portfolio/solving-inverse-kinematics/

Spherical Wrist Manipulator Local Planner for Redundant Tasks in Collaborative Environments, Chiurazzi et. al.
Spherical Shoulder and Wrist
Analytic Inverse Kinematics





IKFast
Kinematic Redundancy

Robot Arm Path Planning Using Modified Particle Swarm Optimization based on D* algorithm, Sadiq et. al.

Part 3
Parametrizing the Constraint Manifold
Parametrization?
Learning the Metric of Task Constraint Manifolds for Constrained Motion Planning, Zha et. al.

Parametrizing the Constraint Manifold


Parametrizing the Constraint Manifold
(Interactive Visualization)
Part 4
Planning with the Parametrization
Sampling-Based Planning
Easy! Just draw samples in the parametrized space
C.f. Atlas-BiRRT (from OMPL)
Trajectory Optimization
C.f. Baseline
GCSTrajOpt
Motion Planning around Convex Obstacles with Convex Optimization, Marcucci et. al.


Motion Planning around Convex Obstacles with Convex Optimization, Marcucci et. al.
Graph of Convex Sets Trajectory Optimization
Constrained Planning with GCSTrajOpt


Path Lengths in Configuration Space
(Asterisk Denotes Collisions)
Online Planning Time (s)
- Can treat the entries of the end-effector transform (e.g. grasp distance) as additional degrees of freedom
- Fix the transform at plan time
Varying the Grasp Distance
Constrained Planning with GCSTrajOpt
What's Next?
Outtakes
" 'Harder Better
Faster Stronger'
-Daft Punk "
-Tommy Cohn

"I can do better than that!"
- Nicholas Pfaff
(Paraphrased)

Work by Shruti Garg
Constrained Bimanual Planning with Analytic Inverse Kinematics (ICRA 2024)
Thomas Cohn, Seiji Shaw, Max Simchowitz, Russ Tedrake



Extra Stuff
(In Case I Have Time)
IRIS: Getting Convex Sets

\(\textrm{FK denotes the Forward Kinematics Map}\)
\(\textrm{Configuration Space}\)
\(\textrm{Task Space}\)
Growing Convex Collision-Free Regions in Configuration Space using Nonlinear Programming, Petersen et. al.
IRIS-NP
IRIS-NP
IRIS-NP
SNOPT
IRIS-NP
IRIS-NP
IRIS-NP
Topology of Kinematics
- Configuration space \(\mathcal{Q}\)
- End-effector space \(\mathcal{X}\)
- Forward kinematics \(f:\mathcal{Q}\to\mathcal{X}\)
- Regular Point: \(q\in\mathcal{Q}\) s.t. \(Df(q)\) is full rank
- Critical Point: \(q\in\mathcal{Q}\) s.t. \(Df(q)\) is singular
- Regular Value: \(x\in\mathcal{X}\) s.t. \(\forall q\in f^{-1}(x)\), \(Df(q)\) is full rank
- Critical Value: \(x\in\mathcal{X}\) s.t. \(\forall q\in f^{-1}(x)\), \(Df(q)\) is singular
- Coregular Value: \(x\in\mathcal{X}\) s.t. \(\exists q_1,q_2\in f^{-1}(x)\) s.t. \(Df(q_1)\) is full rank and \(Df(q_2)\) is singular
Topology of Kinematics (cont'd)
- \(\mathcal{W}\)-Sheet: A connected set of regular and coregular values. Their boundaries are called Critical Value Manifolds.
- \(\mathcal{C}\)-Bundle: A connected set of regular points. Their boundaries are called Coregular Surfaces.
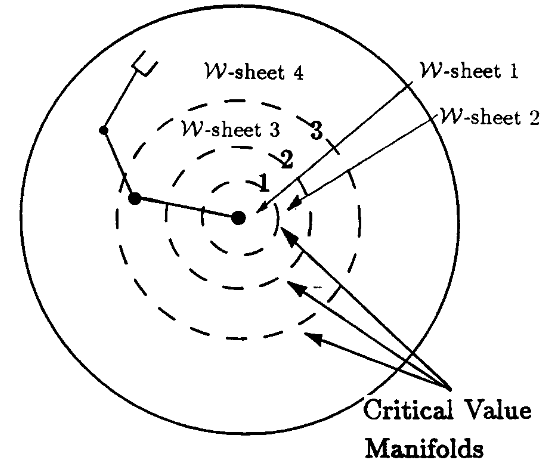
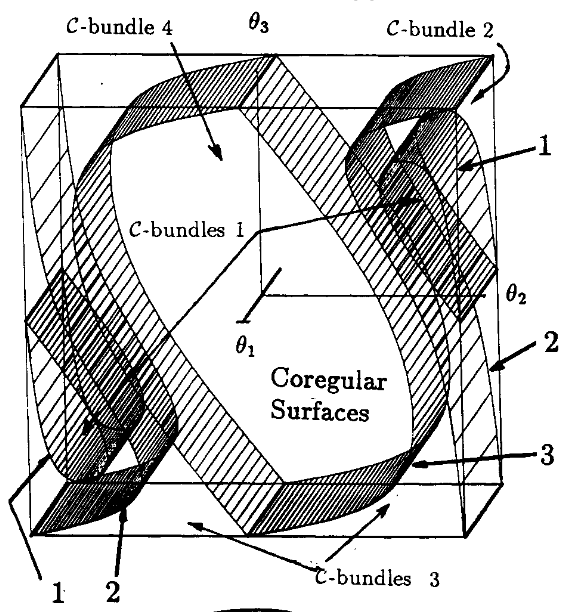
On the inverse kinematics of redundant manipulators: characterization of the self-motion manifolds, Burdick
Making IK a Bijection
- Fix a global configuration
- Treat the redundancy parameter as an argument
- Restrict the domain and range to avoid singularities, etc.
- End effector must stay within a single \(\mathcal{W}\)-sheet
- Joints must stay within a single \(\mathcal{C}\)-bundle