Non-Euclidean Motion Planning with Graphs of Geodesically-Convex Sets

Thomas Cohn, Mark Petersen, Max Simchowitz, Russ Tedrake

Robot Locomotion Group
(Broad) Outline
-
Motivation
- Robot Motion Planning
-
Context
- Mixed-Integer Optimization
- Optimization on Manifolds
-
Our Contributions
- Methodology
- Robot Results
- Generalization
Part 1
Motivation
Motion Planning
Broadly speaking
- How can I get from Point A to Point B?
- What makes a path good?
- Short length
- Short duration
- What constraints might we have?
- Collision avoidance
- Dynamics

Configuration-Space Planning
https://github.com/ethz-asl/amr_visualisations
Task Space
Configuration Space
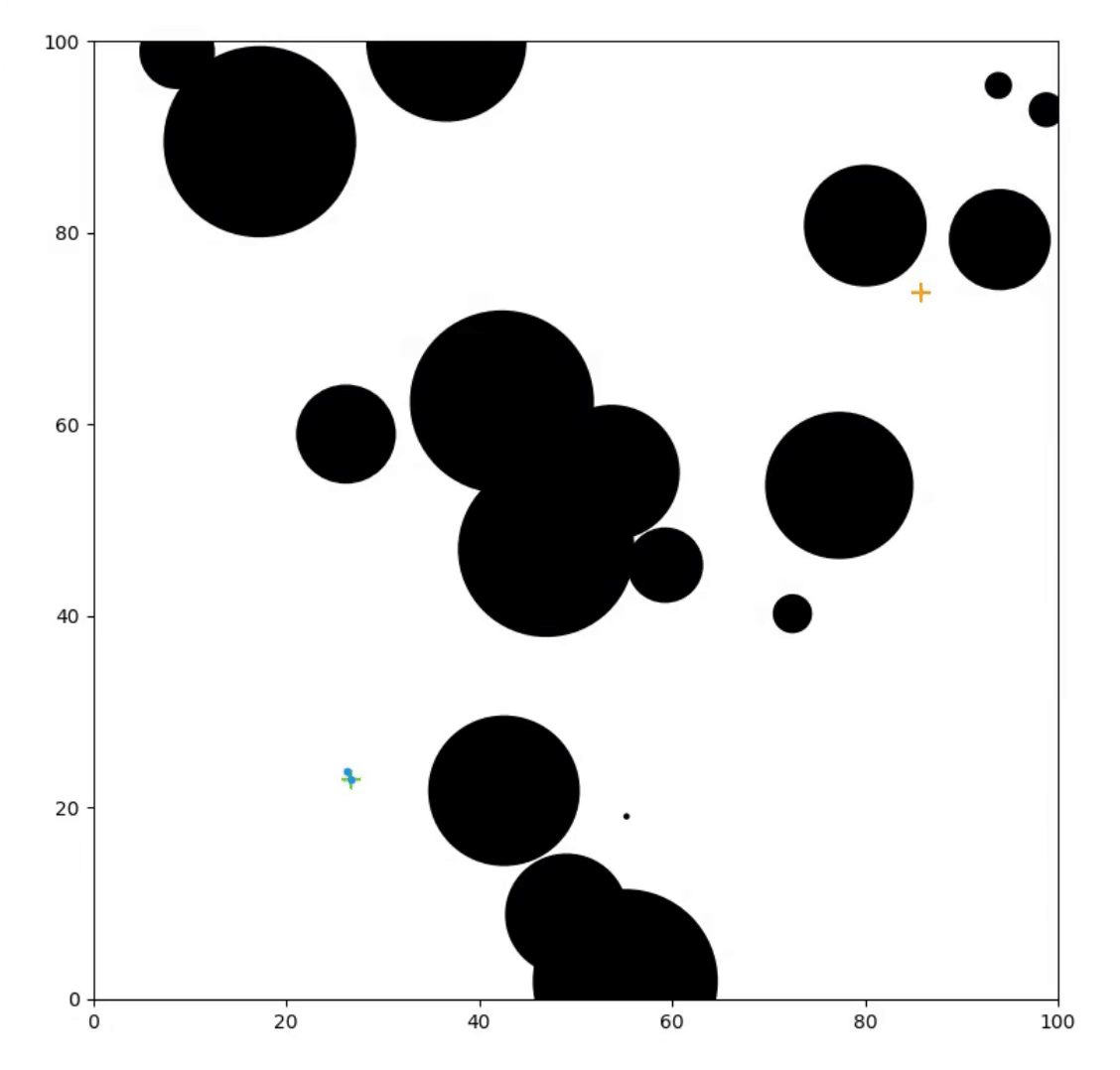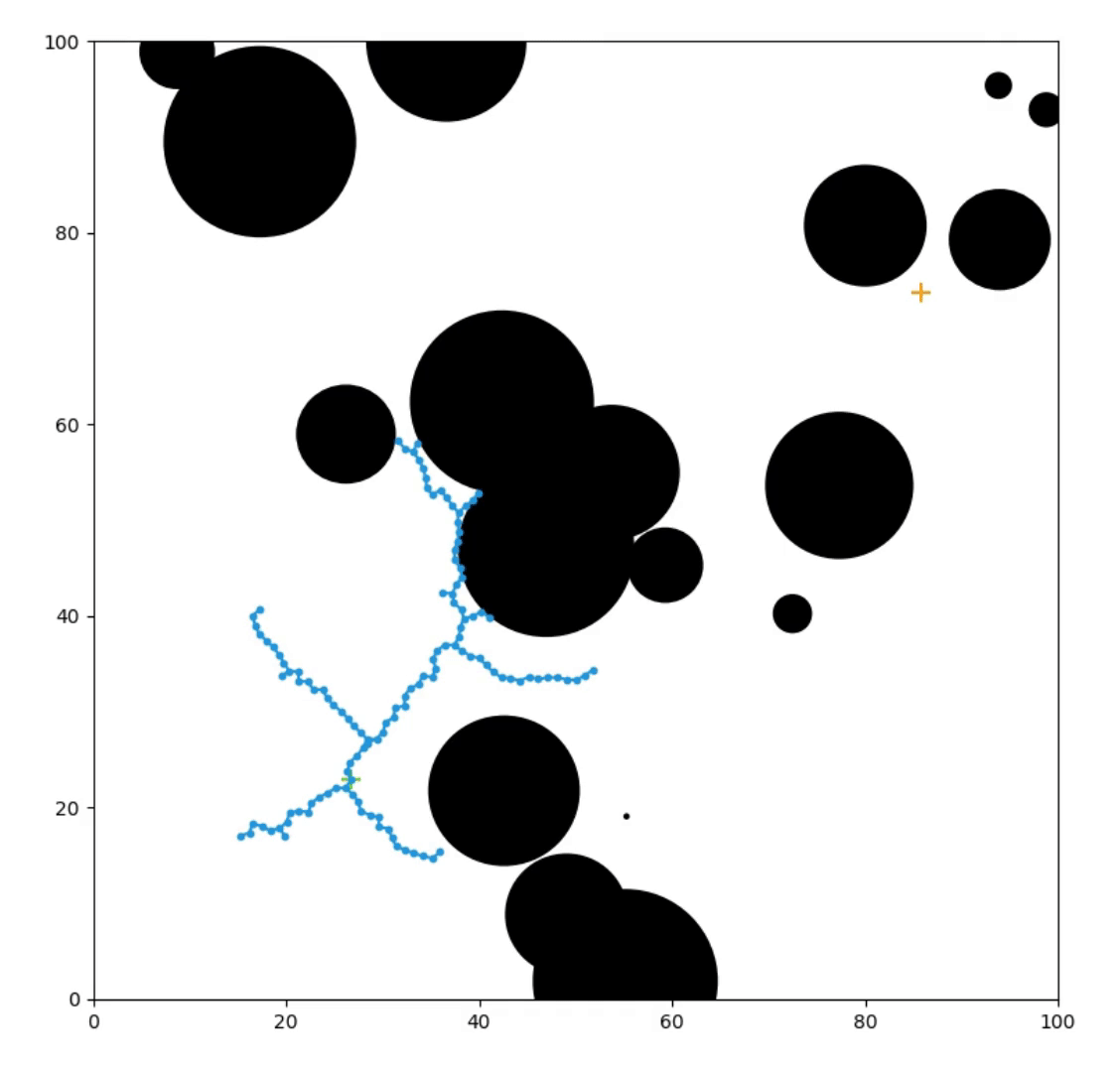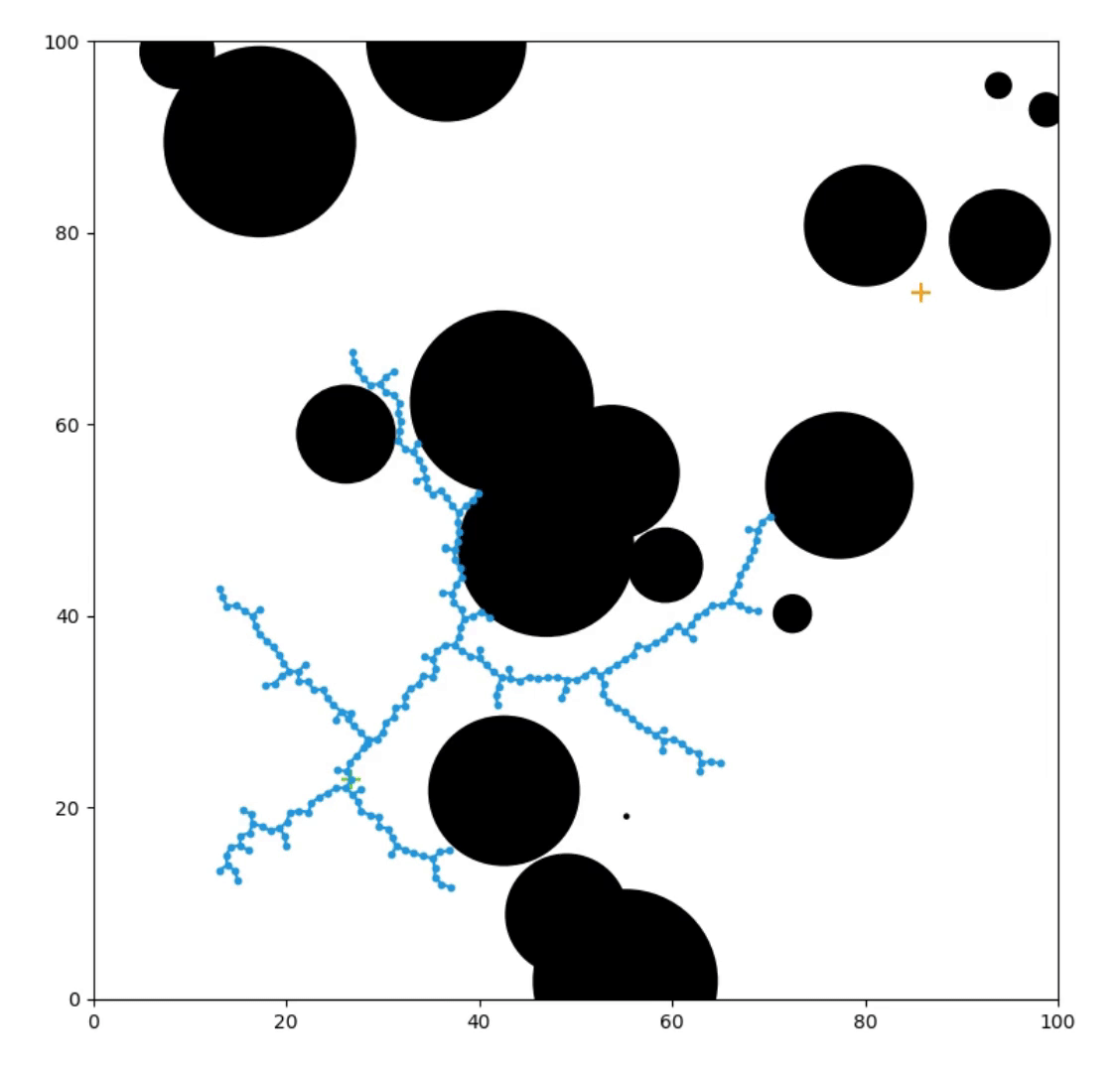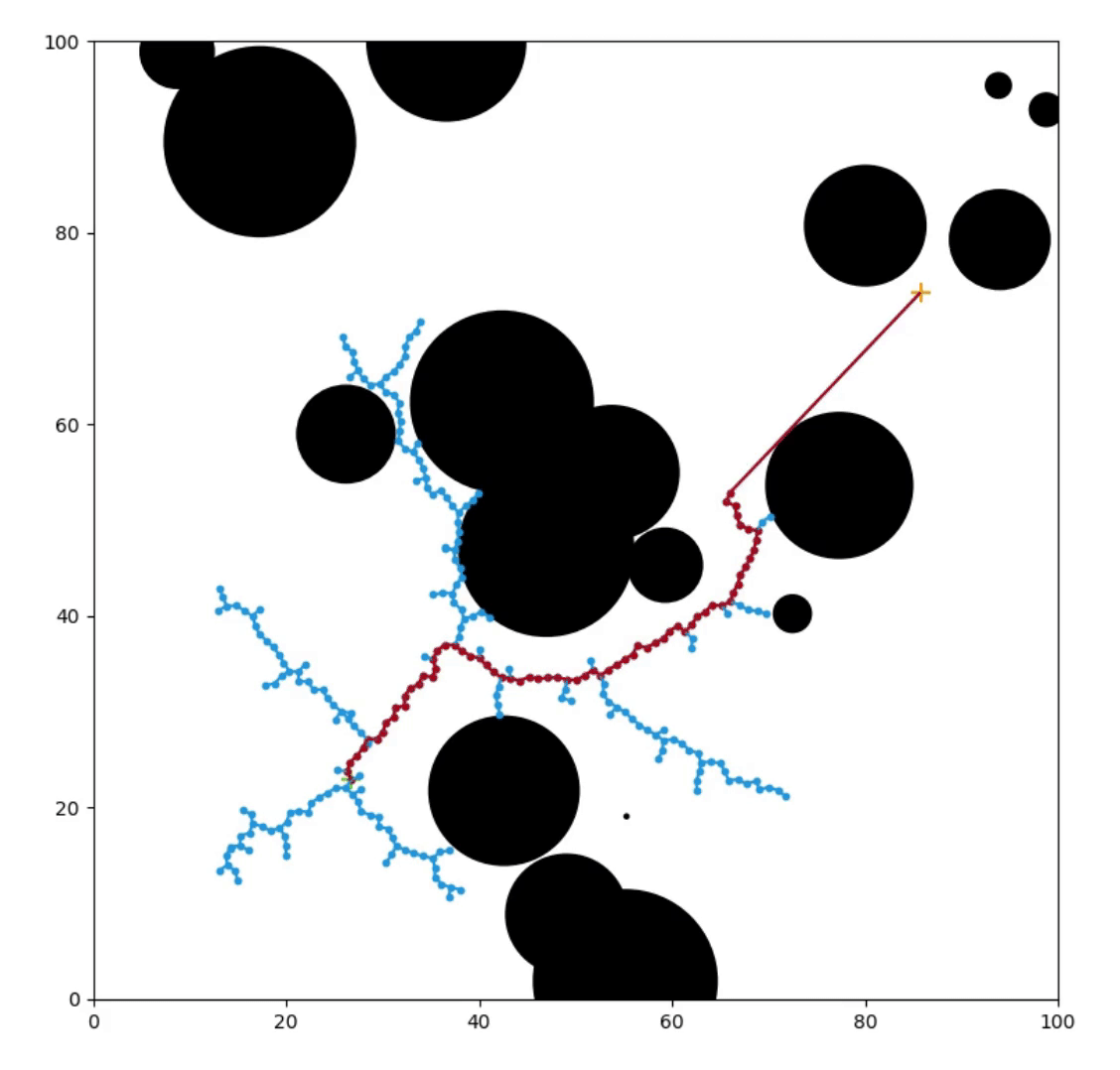
Planning with Roadmaps
Michigan Robotics 320, Lecture 15



Planning with Roadmaps
Pathfinding with Rapidly-Exploring Random Tree, Knox
Trajectory Optimization
Underactuated Robotics

Control points of a trajectory are decision variables.
Use costs and constraints to enforce objectives, dynamics, and more.
Part 2
Context
Nonconvexity in TrajOpt

Planning through Convex Sets
Motion Planning around Convex Obstacles with Convex Optimization, Marcucci et. al.
Obstacle avoidance: nonconvex
Safe-set containment: convex
Obstacle avoidance guarantees!
- Piecewise-linear trajectories: just check endpoints
- Bezier curves: check control points



A Graph of Convex Sets

Configuration Space as a Manifold
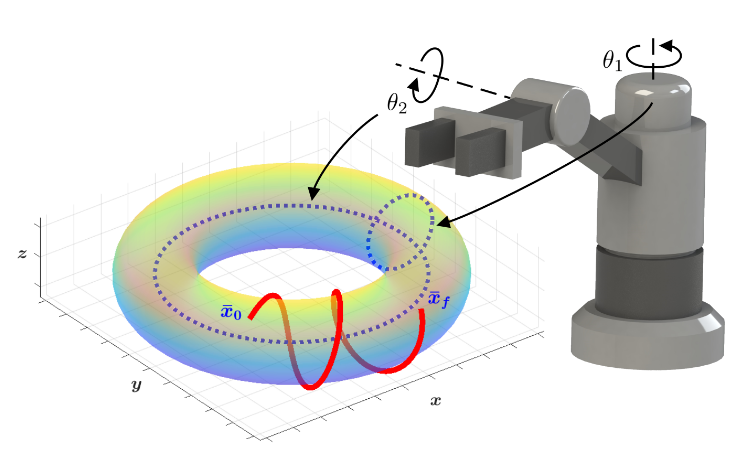
Trajectory Optimization on Manifolds: A Theoretically-Guaranteed Embedded Sequential Convex Programming Approach, Bonalli et. al.
Geodesics: Shortest Paths
For a curve \(\gamma\) connecting two points \(p=\gamma(0),q=\gamma(1)\) on a manifold, its arc length is
\[L(\gamma)=\int_0^1||\dot\gamma(t)||\,\mathrm{d}t\]
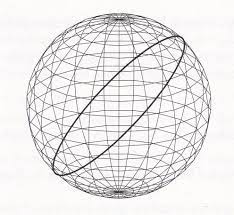
Geodesics on Surfaces by Variational Calculus, Villanueva
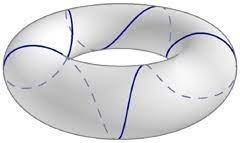
The Curvature and Geodesics of the Torus, Irons
This yields a distance metric
\[d(p,q)=\inf\{L(\gamma)\,|\,\gamma\in\mathcal{C}^{1}_{\operatorname{pw}}([0,1],\mathcal{M}),\\\gamma(0)=p,\gamma(1)=q\}\]
A geodesic is a (locally) length-minimizing curve.
Convex Sets
A set \(X\subseteq\mathbb{R}^n\) is convex if \(\forall p,q\in X\), the line connecting \(p\) and \(q\) is contained in \(X\)
Geodesically Convex Sets
A set \(X\subseteq\mathcal{M}\) is strongly geodesically convex if \(\forall p,q\in X\), there is a unique length-minimizing geodesic (w.r.t. \(\mathcal{M}\)) connecting \(p\) and \(q\), which is completely contained in \(X\).
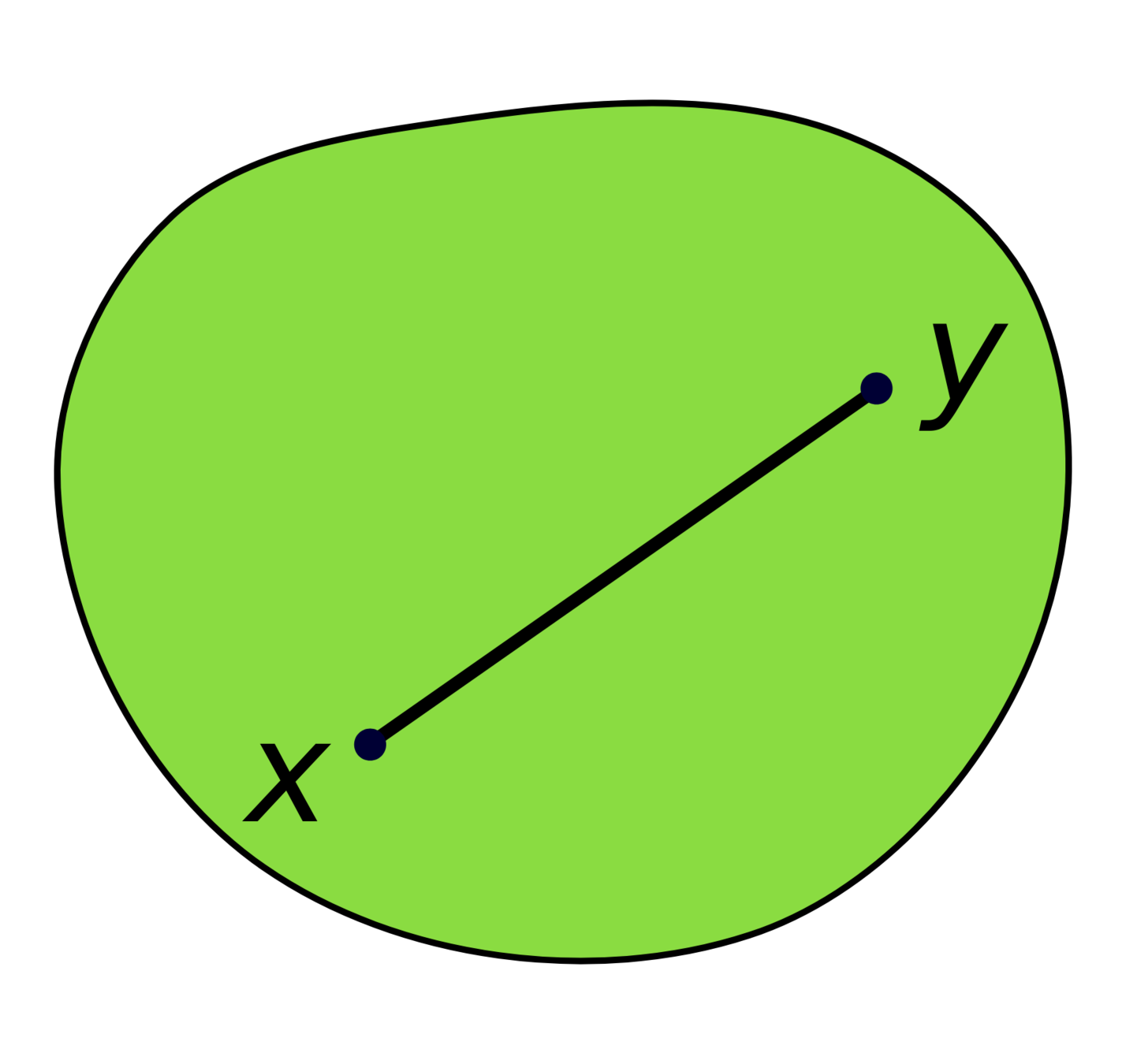
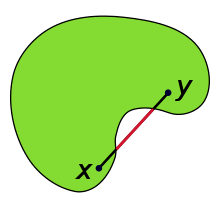
Convex Set, Wikipedia
Some Sets Look Convex
(But Aren't)

Sets can be convex in local coordinates, but not geodesically-convex on the manifold
Geodesics can go "the wrong way around"
Radius of convexity: how large can a set be and still be convex?
Which Continent Is Situated In All Four Hemispheres?, Junior
Convex Functions
A function \(f:X\to\mathbb{R}\) is convex if for any \(x,y\in X\) and \(\lambda\in[0,1]\), we have
\[f(\lambda x+(1-\lambda)y)\le\]
\[\lambda f(x)+(1-\lambda) f(y)\]
Geodesically Convex Functions
A function \(f:\mathcal{M}\to\mathbb{R}\) is geodesically convex if for any \(x,y\in \mathcal{M}\) and any geodesic \(\gamma:[0,1]\to\mathcal{M}\) such that \(\gamma(0)=x\) and \(\gamma(1)=y\), \(f\circ\gamma\) is convex
Part 3a
Methodology
A Graph of Geodesically Convex Sets (GGCS)
A directed graph \(G=(V,E)\)
- For each vertex \(v\in V\), there is a strongly geodesically convex manifold \(\mathcal{Y}_v\)
- For each edge \(e=(u,v)\in E\), there is a cost function \(\ell_e^\mathcal{Y}:\mathcal{Y}_u\times\mathcal{Y}_v\to\mathbb{R}\)
- \(\ell_e^\mathcal{Y}\) must be geodesically convex on \(\mathcal{Y}_u\times\mathcal{Y}_v\)
GCS

GGCS

Transforming Back to a GCS
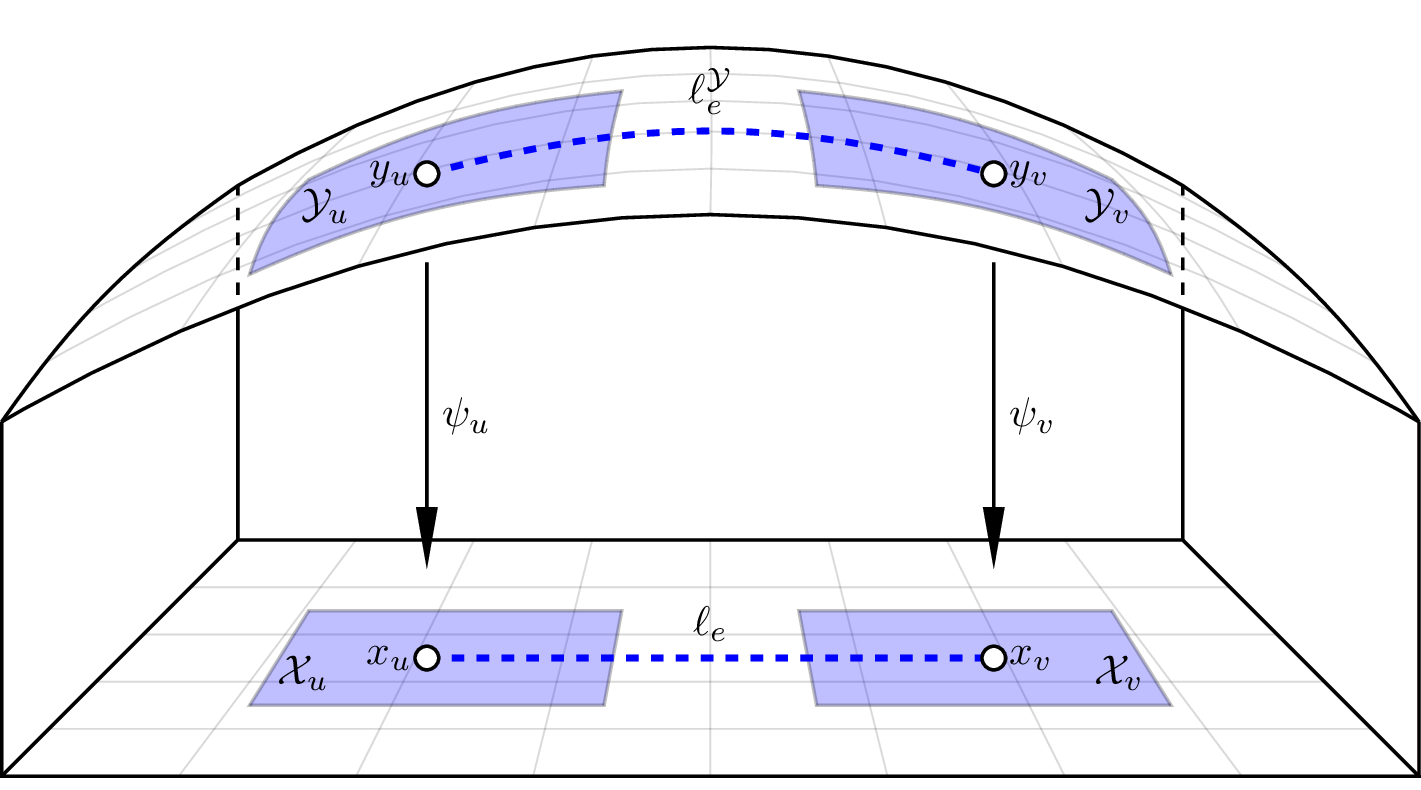
When is it Convex?
Have to consider the curvature of the manifold.
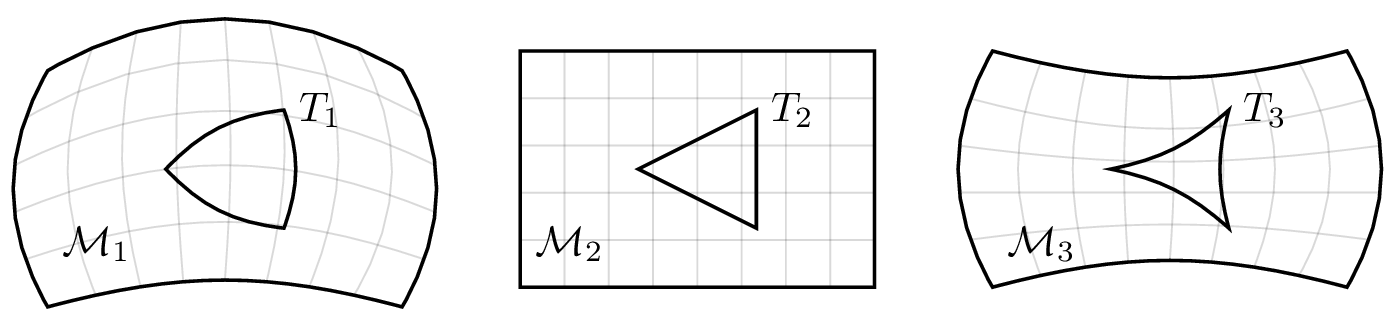
Positive curvature
E.g. \(S^n,\operatorname{SO}(3),\operatorname{SE}(3)\)
Negative curvature
E.g. Saddle, PSD Cone \(\vphantom{S^n}\)
Zero curvature
E.g. \(\mathbb R^n, \mathbb T^n\)


?
Zero-Curvature is Still Useful
- All 1-dimensional manifolds
- Continuous revolute joints
- \(\operatorname{SO}(2)\), \(\operatorname{SE}(2)\)
- Products of flat manifolds
Fetch Robot Configuration
Space: \(\operatorname{SE}(2)\times \mathbb{T}^3\times \mathbb{R}^7\)

Nice Theoretical Results?
- There is a shortest path \(\gamma\) connecting \(p\) to \(q\) through \(\bar{\mathcal{M}}\) such that
- \(\gamma\) is piecewise geodesic
- Each geodesic segment is contained in some \(\bar{X}_u\)
- \(\gamma\) passes through each \(\bar{X}_u\) at most once
-
Ensures that a shortest path is feasible for GGCS
- Transition maps are affine functions (in particular, they are an orthogonal transformation plus a translation)
- Formal equivalence of GGCS and transformed GCS problem
Part 3b
Experimental Results
Part 3c
Generalization
Why is Positive Curvature Bad?
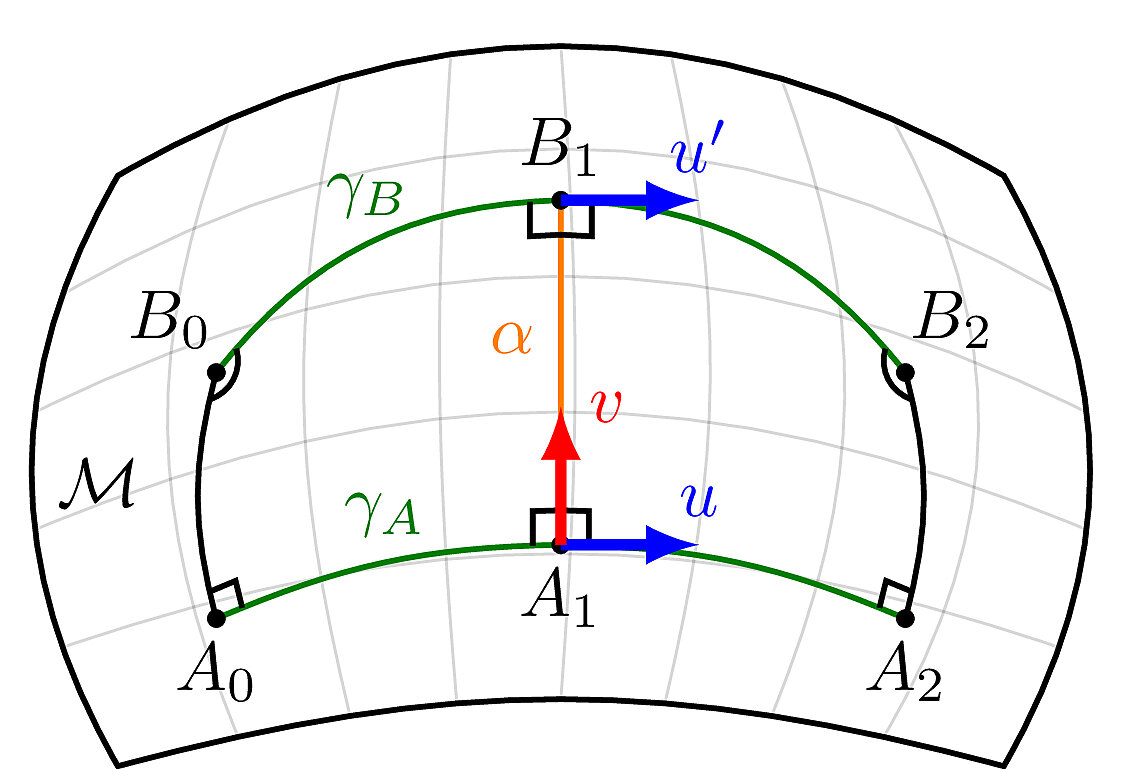
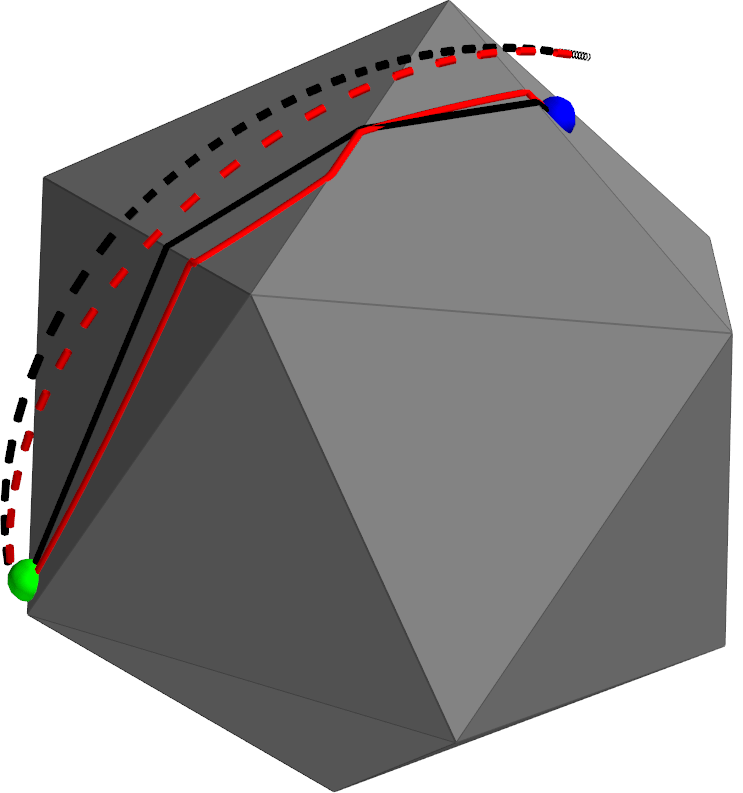


Planning on PL Approximations
Black: Shortest path on PL approximation
Red: Shortest path on sphere
Rough Bounds on Approximation Error
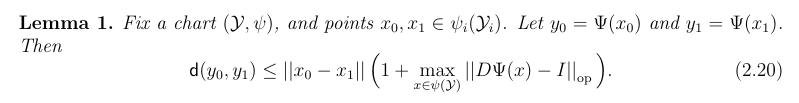
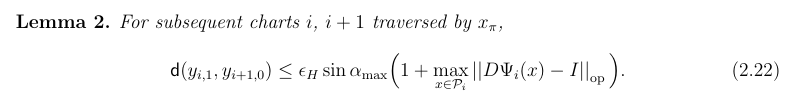
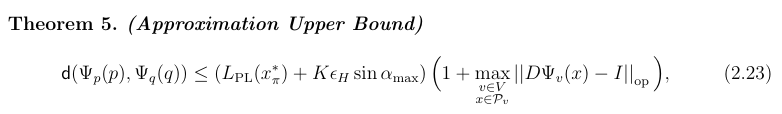
Intuition: How much does the Jacobian of the chart vary?
Intuition: The amount we can "slip" along the boundary also depends on the Hausdorff distance \(\epsilon_H\) between the manifold and its triangulation, as well as the angle \(\alpha_{\operatorname{max}}\) between adjacent charts.
Intuition: The error grows additively with the number of sets traversed in the optimal path.
Focusing on SO(3)/SE(3)
Recall that \(\operatorname{SE}(3)\) is just \(\operatorname{SO}(3)\times\mathbb R^3\)
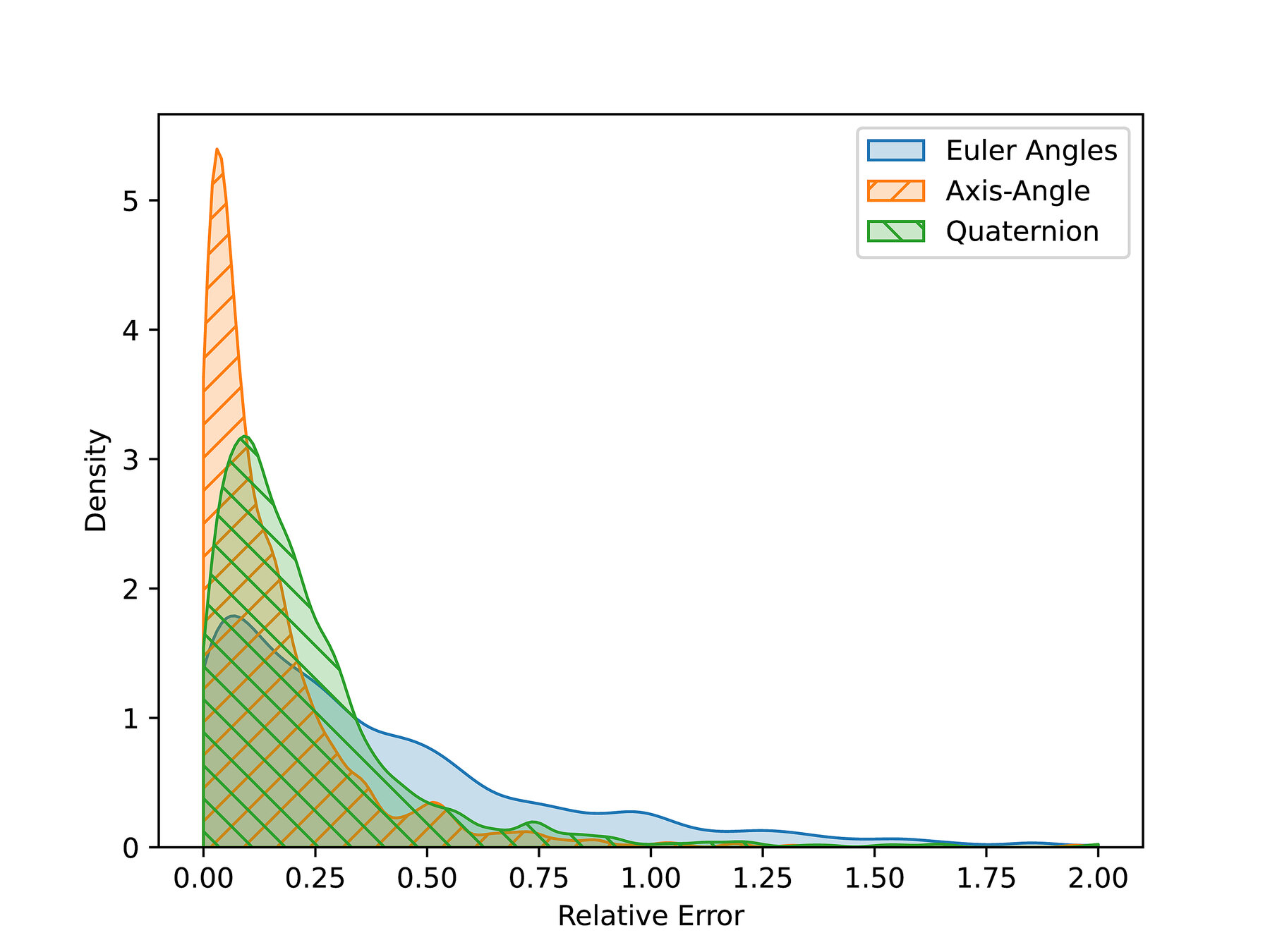
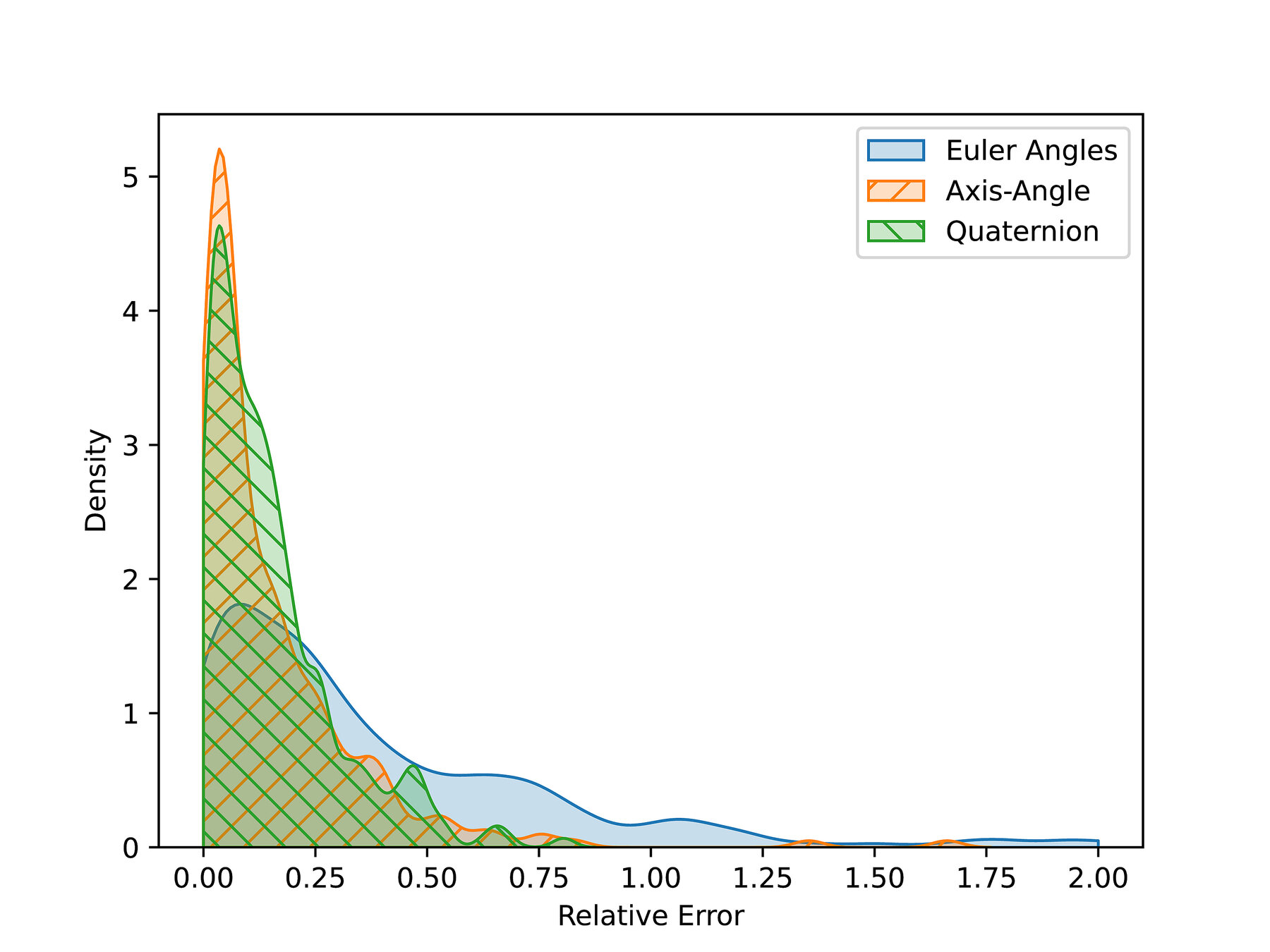
Three representations for \(\operatorname{SO}(3)\):
- Euler angles (\(S^1\times S^1\times S^1\))
- 27 sets, 702 edges (fully connected)
- Axis-angle (\(S^2\times S^1\))
- 60 sets, 660 edges
- Quaternions (\(S^3\))
- 27 sets and 390 edges or 64 sets and 2240 edges
\(S^1\) is flat (no approximation needed)
Numerical Comparison
Randomly sample \(n\) start and goal pairs, plan between them with each approximation.
Compute the true distance, and explore the error distribution.
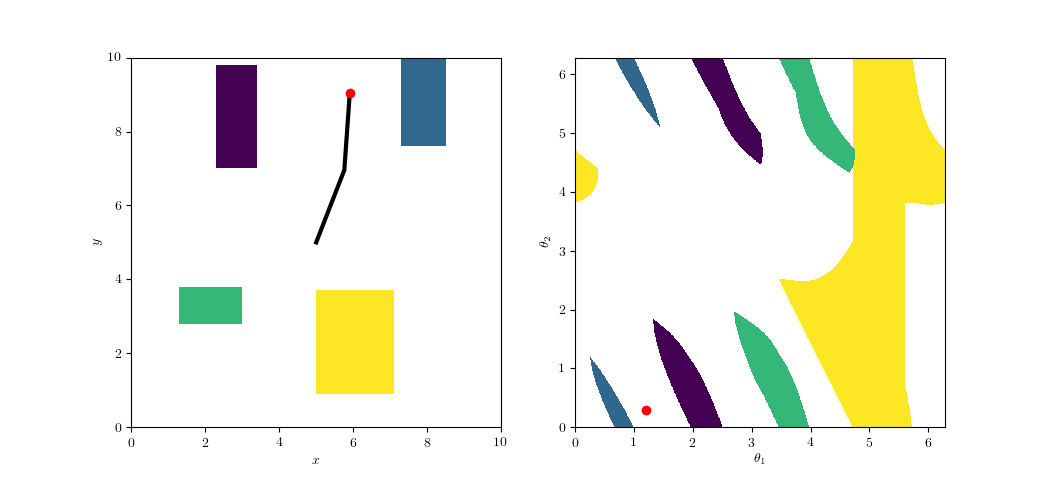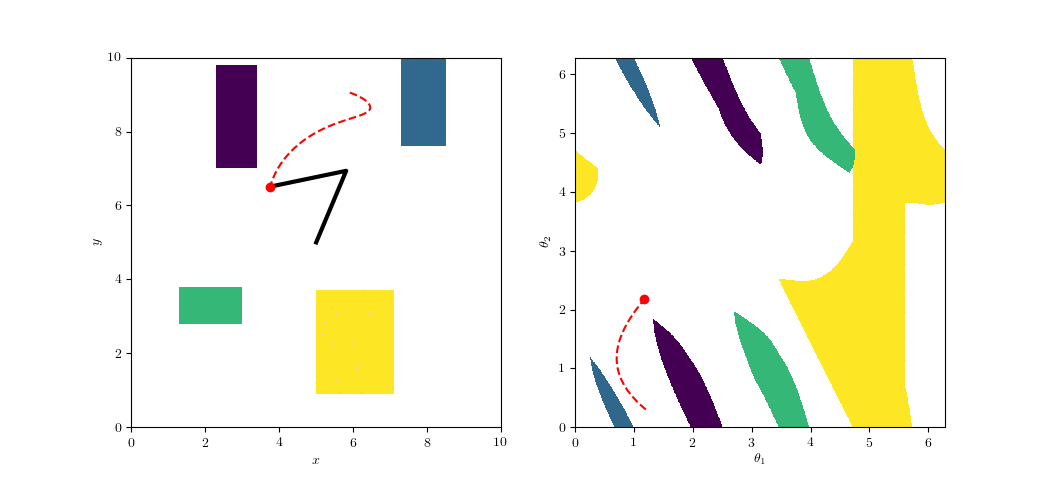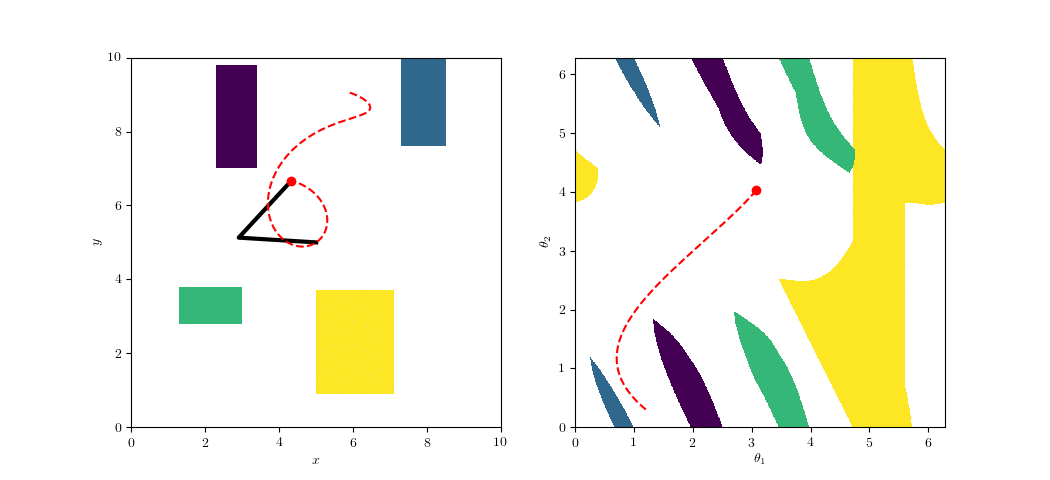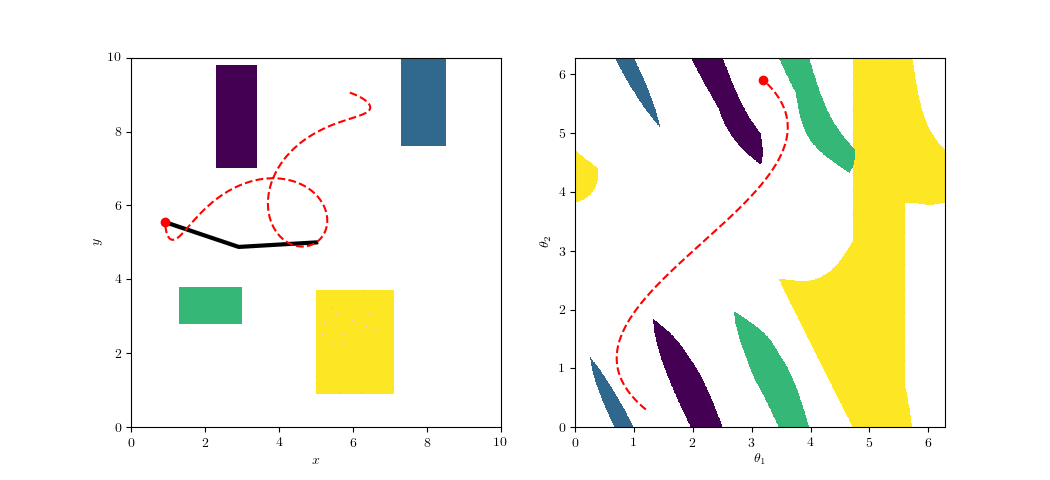
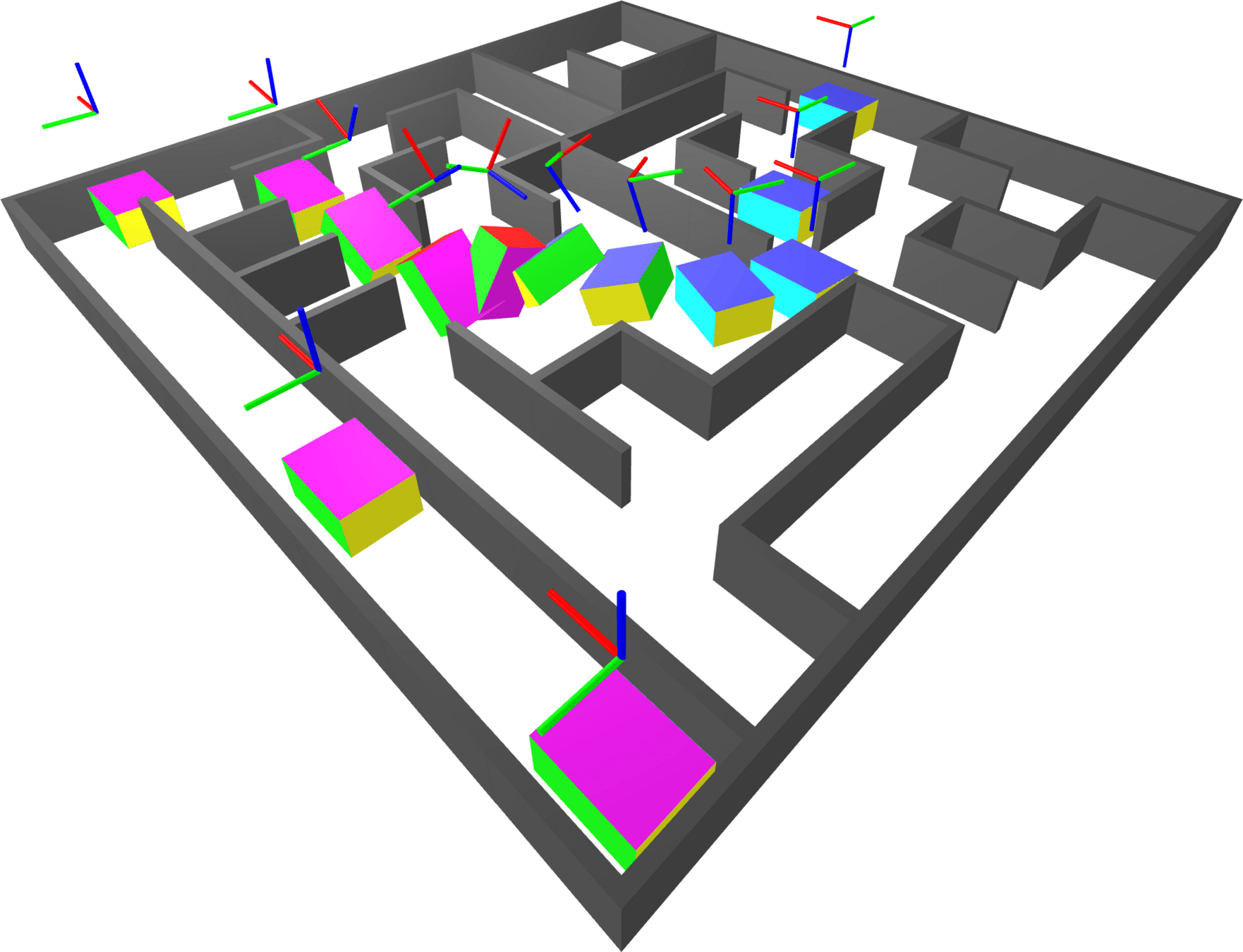
Shortest Paths in the Maze
Sample path between a start/goal pair.
The large gap in the center gives room for the block to reorient itself.
Part 4
Further Work
Bimanual Manipulation
Constrained Bimanual Planning with Analytic Inverse Kinematics, Thomas Cohn, Seiji Shaw, Max Simchowitz, and Russ Tedrake
Nonconvex Objectives
Planning Shorter Paths in Graphs of Convex Sets by Undistorting Parametrized Configuration Spaces, Shruti Garg, Thomas Cohn, and Russ Tedrake

Nonconvex Objectives
Planning Shorter Paths in Graphs of Convex Sets by Undistorting Parametrized Configuration Spaces, Shruti Garg, Thomas Cohn, and Russ Tedrake
Non-Euclidean Motion Planning with Graphs of Geodesically-Convex Sets

Thomas Cohn, Mark Petersen, Max Simchowitz, Russ Tedrake

Robot Locomotion Group