Planning with Discrete Configuration-Space Symmetries

Thomas Cohn

November 22, 2024
(Broad) Outline
- Motivation
- A Background on Quotients and Symmetries
- Methods for Planning with Symmetries
- Results (Completed and Planned)
- What's Next?
Part 1
Motivation
Path Planning
Motion planning's more fundamental cousin
No dynamics, no kinematics, maybe even no robot?
Just asking how to move an object between two configurations.

Object (Dis)Assembly Tasks



Review and taxonomies of assembly and disassembly path planning problems and approaches, Ghandi and Masehian
"Symmetric" Robots

Design, Implementation and Validation of the Three-Wheel Holonomic Motion System of the Assistant Personal Robot (APR), Moreno et. al.
Contact-Rich Manipulation

Efficient Global Planning for Highly Contact-Rich Systems, RQE Presentation, H.J. Terry Suh
Continuous Symmetries
Just drop a dimension!
- Circle: \[\mathbb R^2\times S^1\rightsquigarrow\mathbb R^2\]
- Cylinder: \[\mathbb R^3\times\operatorname{SO}(3)\rightsquigarrow \mathbb R^3\times S^2\]
- Sphere: \[\mathbb R^3\times\operatorname{SO}(3)\rightsquigarrow\mathbb R^3\]
Discrete Symmetries
The dimension stays the same!
There's a fundamental change to the topology of the space that we must take into account.
Planar Pushing with Bernhard
A Symmetry-Unaware Plan
Training Diffusion Policies with Symmetry-Unaware Plans
Does this Work in General?
Symmetric Objects in Practice


What Do I Really Want?
Planning problems with symmetry have additional structure
By exploiting that structure, we should be able to
- Make better motion plans
- Compute plans more quickly
Today's talk: strategies for making symmetry-aware planners
Part 2
Background
Intuition: Quotients as Gluing


Topology, Munkres
Equivalence Relations
An Equivalence Relation \(\sim\) on a set \(X\) is a subset of \(X\times X\) s.t.
- \(x\sim x\) (Reflexivity)
- \(x\sim y\Rightarrow y\sim x\) (Symmetry)
- \(x\sim y,y\sim z\Rightarrow x\sim z\) (Transitivity)
An Equivalence Relation \(\sim\) on a set \(X\) is a subset of \(X\times X\) s.t.
- \(x\sim x\) (Reflexivity)
- \(x\sim y\Rightarrow y\sim x\) (Symmetry)
- \(x\sim y,y\sim z\Rightarrow x\sim z\) (Transitivity)
The equivalence class of an element \(x\in X\) is
\[[x]:=\{y\in X:x\sim y\}\]
Quotient Space
Given an equivalence relation \(\sim\) on \(X\), we can consider the set of equivalence classes \[X/\!\sim\;:=\{[x]:x\in X\}\]
We have the projection map \[\pi:X\to X/\!\sim\quad x\mapsto[x]\]
If \(X\) has certain properties, does \(X/\!\sim\)?
Answer: Sometimes
\(\mathbb R/(2\pi\mathbb Z)\) -- A Worked Example
For \(x,y\in\mathbb R\), define \(x\sim y\;\Leftrightarrow\;(x - y)\bmod 2\pi=0\)
This is an equivalence relation. (Trust me.)
Consider \(\mathbb \R/\sim\), which is often written \(\mathbb R/(2\pi\mathbb Z)\). What are the equivalence classes?
For \(x\in\mathbb R\), we have \([x]=\set{x+2\pi n:n\in\mathbb Z}\)
Quotient Manifolds
If \(X\) is a topological space, we can use \(\pi\) to define the quotient topology on \(X/\!\sim\), where \(Y\subseteq X/\!\sim\) is an open set iff \(\pi^{-1}(Y)\) is open in \(X\). Allows us to discuss quotient manifolds.
https://calculus123.com/wiki/Quotients
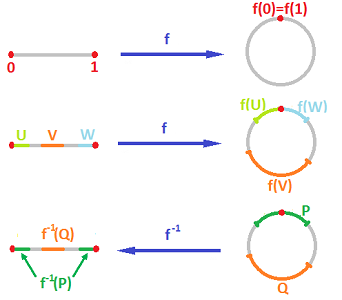
\(0\)
\(2\pi\)
\(\pi\)
\(\pi(0)=\pi(2\pi)\)
Intuition: Quotients as Gluing


Topology, Munkres
Symmetries (Colloquially)
Symmetry Groups
A group \((G,\cdot)\) is a set \(G\) with an operation \(\cdot:G\times G\to G\) such that...
- Identity element: \(\exists e\in G\) such that \(\forall g\in G\), \(e\cdot g=g\).
- Inverse elements: \(\forall g\in G\), \(\exists g^{-1}\in G\) such that \(g\cdot g^{-1}=e\).
- Closed under the group operation: \(\forall g,h\in G\), \(g\cdot h\in G\).
Example of a group: rotations in 2D
- Identity element is the \(2\times 2\) identity matrix
- Every rotation has an inverse
- The composition of two rotations is a rotation
From now on, we just write \(gh\) instead of \(g\cdot h\)
Group Actions
A group \((G,\cdot)\) acts on a set \(X\) via the function \(\alpha:G,X\to X\) if...
- Identity property: \(\forall x\in X\), \(\alpha(e,x)=x\).
- Compatibility: \(\forall g,h\in G,x\in X\), \(\alpha(g,\alpha(h,x))=\alpha(gh,x)\).
Example of a group action: rotations acting on points in 2D
\[\alpha:\operatorname{SO}(2)\times\mathbb R^2\to\mathbb R^2\]
\[\left(\begin{pmatrix}\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta\end{pmatrix},\begin{pmatrix}x\\ y\end{pmatrix}\right)\mapsto \begin{pmatrix}\cos\theta & -\sin\theta\\ \sin\theta & \cos\theta\end{pmatrix}\begin{pmatrix}x\\ y\end{pmatrix}\]
For notational brevity, usually we write \(\alpha(g,x)=g\cdot x\).
A Specific Symmetry Group
Let's discuss the symmetry group of a square
Four elements:
\[\begin{pmatrix}1, 0\\ 0, 1\end{pmatrix},\;\begin{pmatrix}0, -1\\ 1, 0\end{pmatrix},\;\begin{pmatrix}-1, 0\\ 0, -1\end{pmatrix},\;\begin{pmatrix}0, 1\\ -1, 0\end{pmatrix}\]
(Matrix multiplication is the group operation.)
Orbits as Equivalence Classes
Then \([x]\) corresponds to the orbit \(g\cdot x=\{g\cdot x:g\in G\}\).
Given a group \(G\) acting on \(X\), for \(x,y\in X\), let \(x\sim y\) if \(\exists g\in G\) such that \(g\cdot x=y\).
Notation: \(X/\sim\) is written as \(X/G\)
The Geometry of Symmetries
Let \(\mathcal M\) be the configuration space of a rigid body (represented as a smooth manifold). Let \(G\) be the group of symmetries acting on the object.
Theorem: (Quotient Manifold Theorem) If certain conditions* are satisfied, then \(\mathcal M/G\) is also a smooth manifold.
*See Introduction to Smooth Manifolds, Lee, Chapter 21, for details.
The Riemannian Case
Under certain further conditions (which are satisfied by the symmetry groups of rigid bodies), \(\mathcal{M}/G\) gets a Riemannian metric from \(\mathcal{M}\).
For a finite group \(G\), this is just a minimum of finitely many elements, so it can be efficiently computed!
Furthermore, the distance function takes the following form: \[d([x],[y])=\inf\{d(x,y):x\in[x],y\in[y]\}\]
When we're working over \(\operatorname{SO}(2)\) or \(\operatorname{SO}(3)\), \(d(x,y)\) is known in closed-form.
Finite Subgroups of SO(2)
The possible symmetries in 2D are those of a regular n-gon.
Finite Subgroups of SO(3)
More complicated...
- Symmetries of a pyramid with a regular n-gon base
- Symmetries of a prism with a regular n-gon base
- Symmetries of the platonic solids
- Tetrahedron
- Cube/Octahedron
- Dodecahedron/Icosahedron
Some Related Literature...
Planning with Discrete Decisions
Disjunctive constraints are always an option. To plan from \([s]\) to \([t]\) where \(x\) is the last point in the trajectory, require
\[\prod_{t'\in[t]}(x-t')=0.\]
A better option: DDP with discrete decisions (Trajectory Optimization with Discrete Decisions, Scott et. al.)

Planning on Quotient Manifolds
See Multilevel motion planning: A fiber bundle formulation, Orthey et. al.
This can only be made to handle continuous symmetries (each quotient must be positive dimension)

Sampling-Based Planning
Trajectory Optimization
Planning on Arbitrary Manifolds
Sampling-Based Methods for Motion Planning with Constraints, Kingston et. al.
Direct Collocation Methods for Trajectory
Optimization in Constrained Robotic Systems, Bordabla et. al.
Embedding SO(3)/G
Whitney and Nash: such embeddings exist.
Not very helpful!

Nice, but maybe not the direction we want to take...
Part 3
Methodology
Universal Naive Strategies
- Ignore the symmetry and plan between an arbitrary representative of the start and goal
- Plan between all possible combinations of representatives of starts and goals
- Because the group action can be applied to a whole trajectory, can pick either a single start or goal.
Sampling Based Planning (SBP)
Focus on the IMACS framework (Implicit Manifold Configuration Space)
\(\rightarrow\) Introduced by Kingston et. al. in Exploring implicit spaces for constrained sampling-based planning.
Key idea: reduce SBP on manifolds to a set of primitives, so that arbitrary SBP algorithms can be mixed-and-matched with different representations on manifolds
| RRT | PRM | |
|---|---|---|
| Continuation | x | x |
| Projection | x | x |
IMACS Primitives
- Distance Metric between \([s]\) and \([t]\)
- Fix any \(s\in[s]\), and \(d_{\mathcal M/G}([s],[t])=\min_{t\in[t]}d_{\mathcal M}(s,t)\).
- Finite minimum, so easily computable!
- Global Uniform Sampling
- Just draw uniform samples from \(\mathcal M\) and project.
- This will be a uniform distribution on \(\mathcal M/G\).
- Local Sampling around \([q]\in\mathcal M/G\)
- Pick a representative \(q\in[q]\), draw samples in a ball around \(q\), and project.
- Will be reasonable if the ball is small.
IMACS Primitives
- Distance Metric between \([s]\) and \([t]\)
- Fix any \(s\in[s]\), and \(d_{\mathcal M/G}([s],[t])=\min_{t\in[t]}d_{\mathcal M}(s,t)\).
- Finite minimum, so easily computable!
- Local Planning from \([s]\) to \([t]\)
- Compute trajectory from any \(s\in[s]\) to \(\argmin_{t\in[t]}d_{\mathcal M}(s,t)\).
- Geodesics in \(\operatorname{SO}(2)\) and \(\operatorname{SO}(3)\) known in closed-form.
- Oftentimes can be computed concurrently with the distance metric.
Planning with IMACS
All methods use local planning to connect nodes
- KNN/Radius PRM
- Uniform sample to get the nodes
- Distance metric to determine possible neighbors
- RRT
- Uniform sample to get next node
- Distance metric to find closest neighbor
- Expansive Space Tree (EST)
- Local sample around existing nodes to find new ones
- Distance metric to estimate neighborhood density
Trajectory Optimization
I really think disjunctive costs or constraints are a bad idea
So what else can we do? How can we encode discrete decisions in a trajectory optimization framework?

Network Flow Problems
GCS can be thought of as a generalization of min-cost flow.

6.7210 Lecture 16, 2022, Jaillet
Redundant Sources/Sinks
"Every network flow problem can be reduced to one with exactly one source and exactly one sink node." Introduction to Linear Optimization, Bertsimas and Tsitsiklis, page 274

Part 4
Results
2D Path Planning Infrastructure
- Random world generation
- Assorted Objects









Proof-of-Concept Results
Some Numerical Results 1
Triangle Symmetry, KNN-PRM with k=15, 500 nodes
- Symmetry-Aware Build Time: 22 seconds
- Symmetry-Unaware Build Time: 23 seconds
Planning between 100 start and goal pairs.
- Symmetry aware had a 95% success rate, symmetry-unaware was 94%.
- (C-Space may be disconnected.)
- Symmetry-aware paths were 86.9% the length of the symmetry-unaware paths (standard deviation of 13.3%)
- 90.4% of symmetry-aware paths were shorter
Some Numerical Results 2
Triangle Symmetry, KNN-PRM with k=25, 1000 nodes
- Symmetry-Aware Build Time: 113 seconds
- Symmetry-Unaware Build Time: 95 seconds
Planning between 100 start and goal pairs.
- Both algorithms had a 91% success rate.
- (C-Space may be disconnected.)
- Symmetry-aware paths were 88.3% the length of the symmetry-unaware paths (standard deviation of 10.2%)
- 94.5% of symmetry-aware paths were shorter
Some Numerical Results 3
Pentagonal Symmetry, KNN-PRM with k=25, 1000 nodes
- Symmetry-Aware Build Time: 88 seconds
- Symmetry-Unaware Build Time: 111 seconds
Planning between 100 start and goal pairs.
- Both algorithms had a 85% success rate.
- (C-Space may be disconnected.)
- Symmetry-aware paths were 84.1% the length of the symmetry-unaware paths (standard deviation of 12.9%)
- 96.5% of symmetry-aware paths were shorter
Some Numerical Results 4
Octagonal Symmetry, KNN-PRM with k=25, 1000 nodes
- Symmetry-Aware Build Time: 98 seconds
- Symmetry-Unaware Build Time: 108 seconds
Planning between 100 start and goal pairs.
- Both algorithms had a 72% success rate.
- (C-Space may be disconnected.)
- Symmetry-aware paths were 84.1% the length of the symmetry-unaware paths (standard deviation of 19.8%)
- 95.8% of symmetry-aware paths were shorter
Some Observations
- Higher symmetries lead to shorter edges, so faster build times.
- Radius PRM adds more edges with symmetries
- Shortcutting probably helps a ton
3D Path Planning Infrastructure






- Assorted Objects
- Random world generation TODO
- (2D framework should generalize directly.)
- Results forthcoming
Symmetry Unaware Planar Pushing
Symmetry Aware Planar Pushing
Planned Numerical Results
- 2D/3D Path Planning
- Algorithms: naive and smart versions of KNN-PRM, Radius-PRM, GCS
- Statistics across many random worlds, different seeds for PRM generation per world, random start-goal pairs, different symmetric objects.
- Planar Pushing
- Algorithms: naive and smart versions of GCS
- In-Hand Reorientation
- Algorithms: naive and smart versions of PRM
Planned Demonstrative Results
- 2D/3D Path Planning
- Object assembly examples?
- Planar Pushing
- Better diffusion policies trained from the symmetry-aware planner
- Additional obstacles in the world?
- In-Hand Reorientation
- Hardware demos?
Further Quetsions
- Sampling-Based Planning
- Evaluating RRT performance (Do they get better or worse? Why?)
- GCS
- Can we be smarter than just having multiple goals?
- There should be some way to make the sets live in the quotient space?
Planning with Discrete Configuration-Space Symmetries

Thomas Cohn

November 22, 2024