Non-Euclidean Motion Planning with Graphs of Geodesically-Convex Sets

Thomas Cohn, Mark Petersen, Max Simchowitz, Russ Tedrake

June 9, 2023
(Broad) Outline
- Motivation
- Theoretical Background
- Motion Planning in Non-Euclidean Spaces
- Results
- Next Steps and Future Directions
Part 1
Motivation
Motion Planning Today
- Sampling-based planning
-
+
Global optimality -
-
Curse of Dimensionality -
-
"RRT Dance"
-
- Trajectory optimization
-
-
Nonconvex -- not optimal -
+
Scales with dimension -
+
Smooth paths, dynamics
-
Motion Planning, Wikipedia


Also: collision avoidance?
Motion Planning Today
- Sampling-based planning
-
+
Global optimality -
-
Curse of Dimensionality -
-
"RRT Dance"
-
- Trajectory optimization
-
-
Nonconvex -- not optimal -
+
Scales with dimension -
+
Smooth paths, dynamics
-
Wikipedia


Also: collision avoidance?
Planning through Convex Sets
Motion Planning around Convex Obstacles with Convex Optimization, Marcucci et. al.
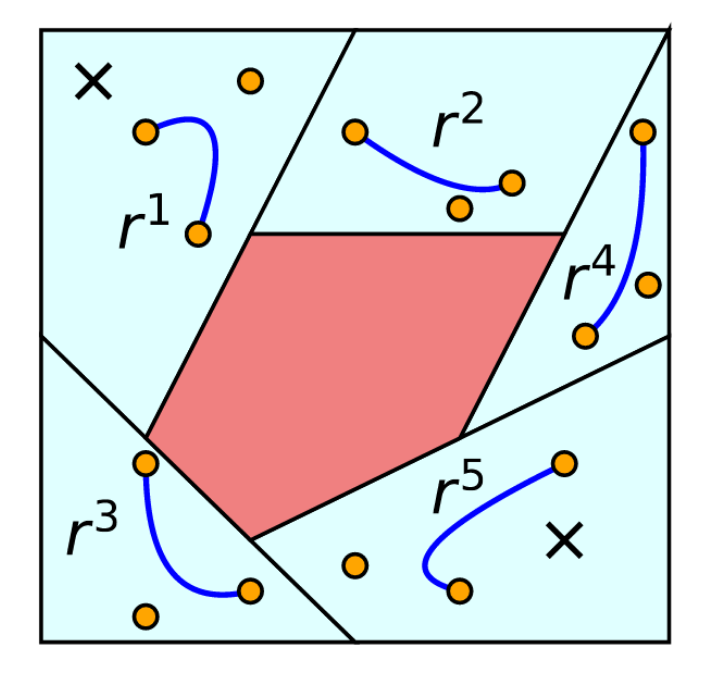
Obstacle avoidance: nonconvex
Safe-set containment: convex
Obstacle avoidance guarantees!
- Piecewise-linear trajectories: just check endpoints
- Bezier curves: check control points
Motion Planning with GCS
- Represent C-Free with convex sets
- Formulate shortest path problem as MICP
- Can solve to optimality (branch and bound)
- In practice, relax and round yields a good result
Shortest Paths in Graphs of Convex Sets, Marcucci et. al.
Motion Planning around Convex Obstacles with Convex Optimization, Marcucci et. al.

What about non-Euclidean configuration spaces?
What Is a Non-Euclidean Configuration Space?
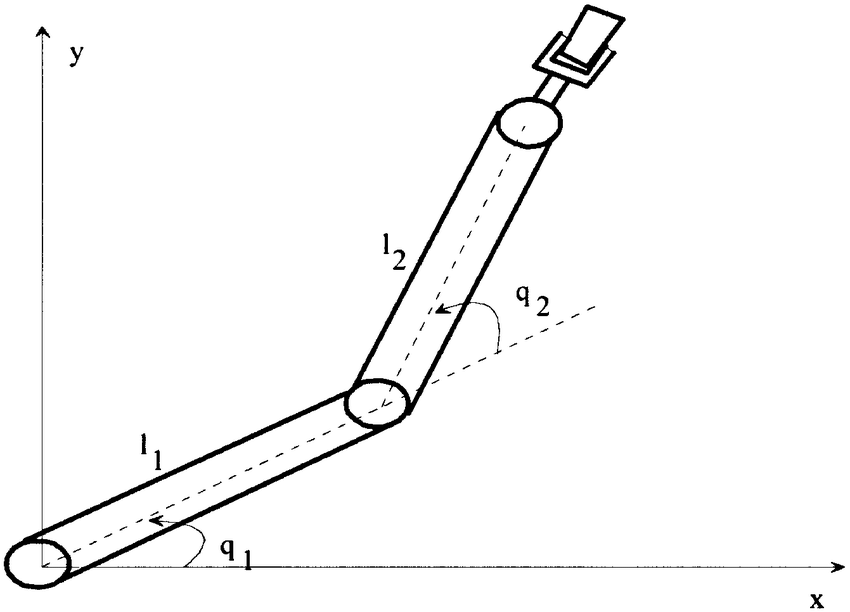
Robust Combined Adaptive and Variable Structure Adaptive Control of Robot Manipulators, Yu
(No joint limits)
Survey of Graph Embeddings into Compact Surfaces, Potoczak
"Locally" Euclidean Spaces
?
?
?
?
Manifolds

?
?
?
?
Part 2
Theoretical Background
Continuity (Intuition)
Continuous functions take nearby points to nearby points

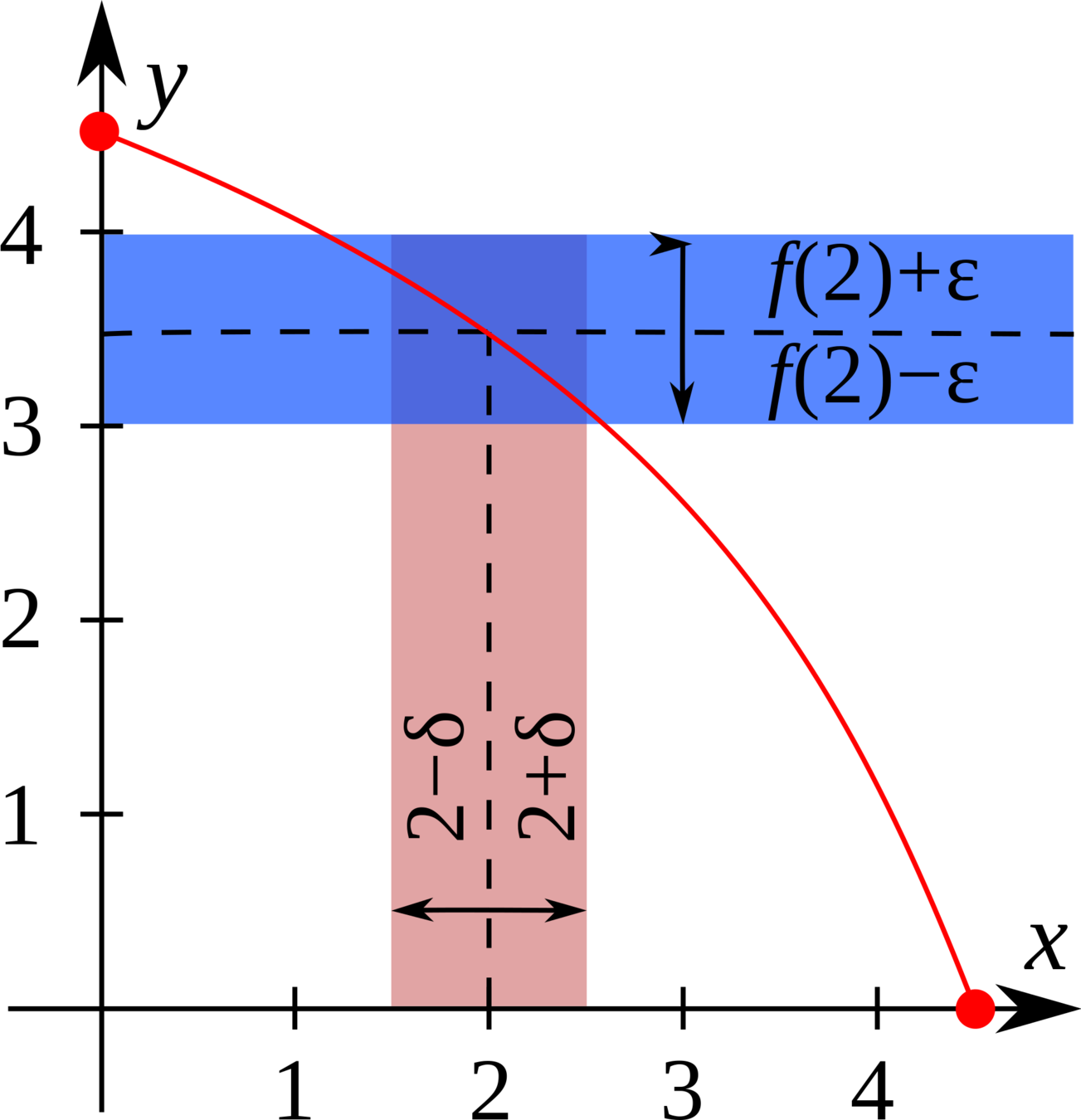
What is a Topological Space?
A rule for which functions are continuous by defining what "nearby" means
Explicitly: a rule for constructing arbitrarily small* neighborhoods around points
Examples:

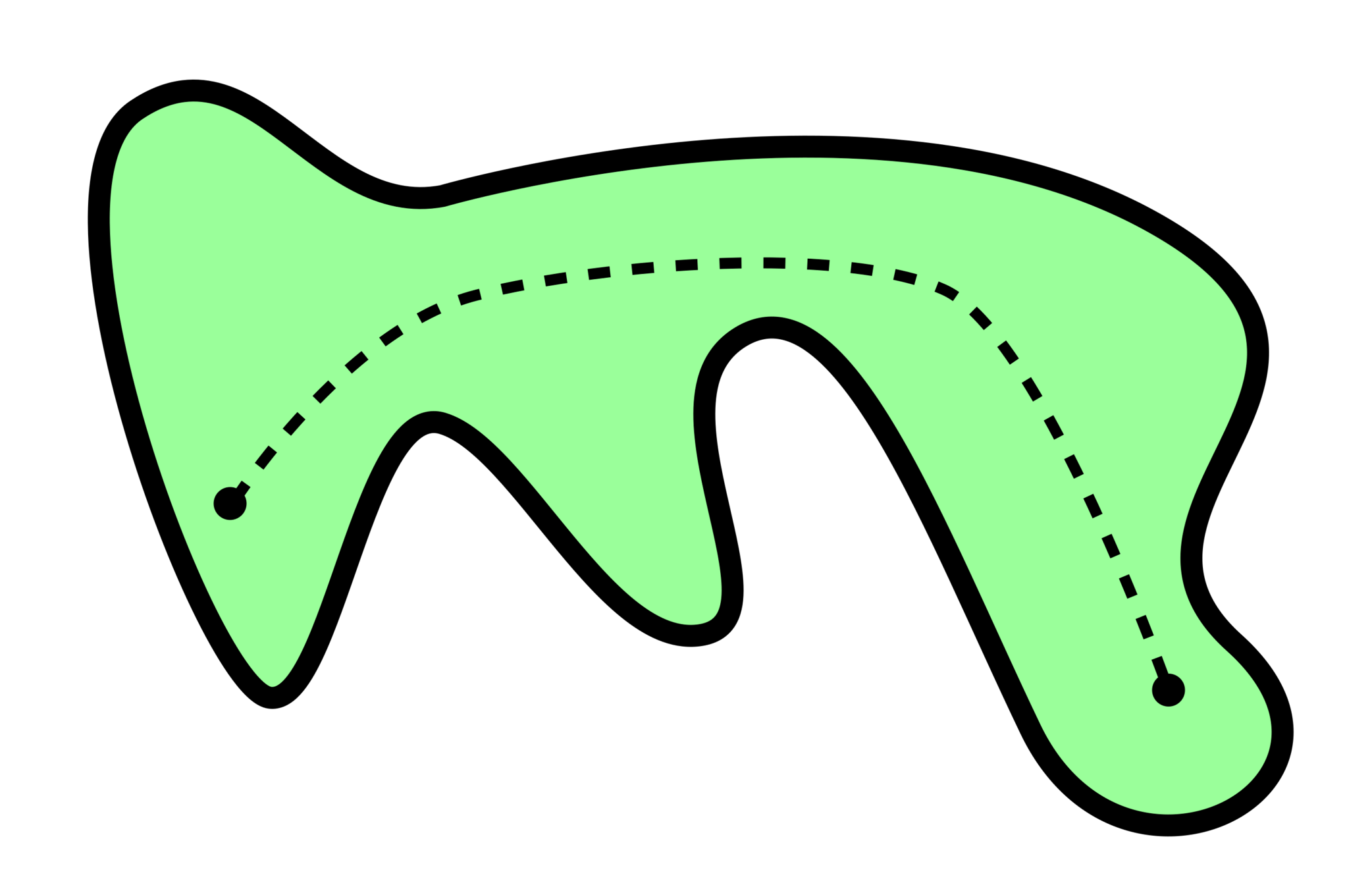
(Path) Connectedness
A topological space is path connected if there is a continuous curve joining any two points.
A continuous curve is the image of a function \(f:[0,1]\to X\)

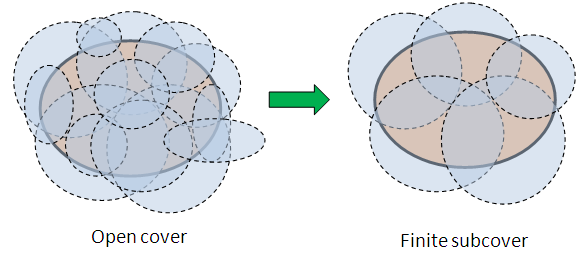
Compactness
A set is compact if every open cover has a finite subcover
Heine-Borel Theorem: In Euclidean spaces, compact iff closed and bounded
Extreme Value Theorem: Functions over compact sets have max and min values (useful for optimization theory)
Topology Summary
-
Continuity
- Does a function map nearby points to nearby points?
-
Path-Connectedness
- Can one "move" between two points?
-
Compactness
- Do functions have extrema?
Definition of a Manifold
A (topological) manifold is a locally-Euclidean topological space
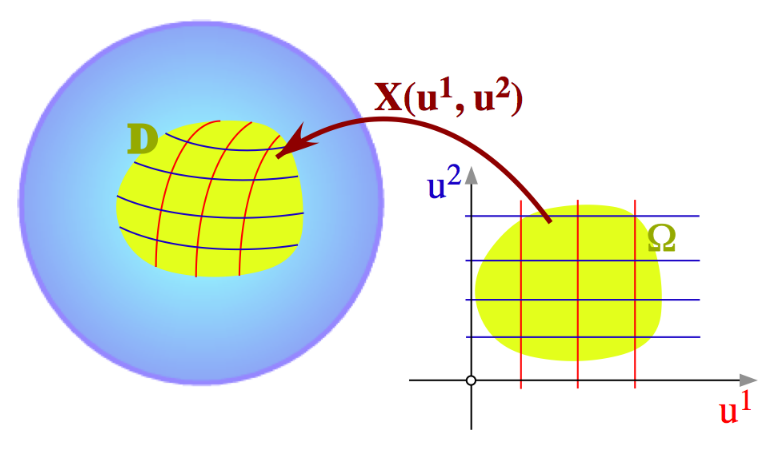
Mapping the Earth, Treibergs
Definition of a Manifold
A (topological) manifold is a locally-Euclidean topological space
Introduction to Smooth Manifolds, Lee
Definition of a Manifold
Locally-Euclidean: any \(x\in\mathcal{M}\) is contained in an open set \(U\subseteq\mathcal{M}\) such that \(U\) is homeomorphic to a subset of Euclidean space

Introduction to Smooth Manifolds, Lee
A (topological) manifold is a locally-Euclidean topological space
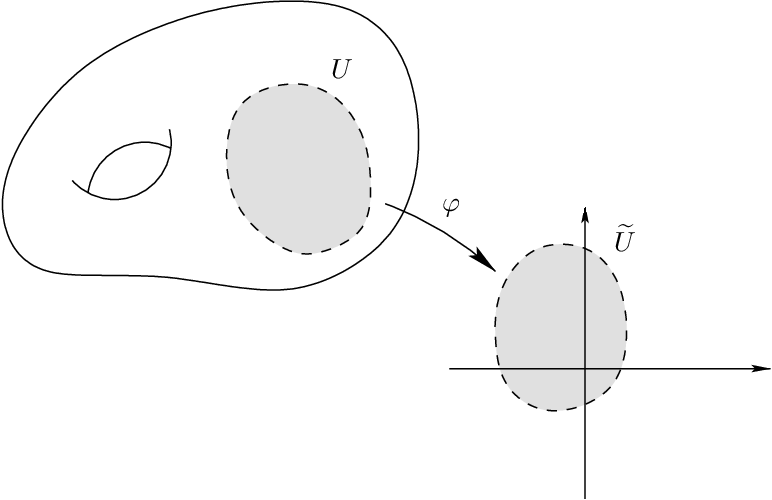
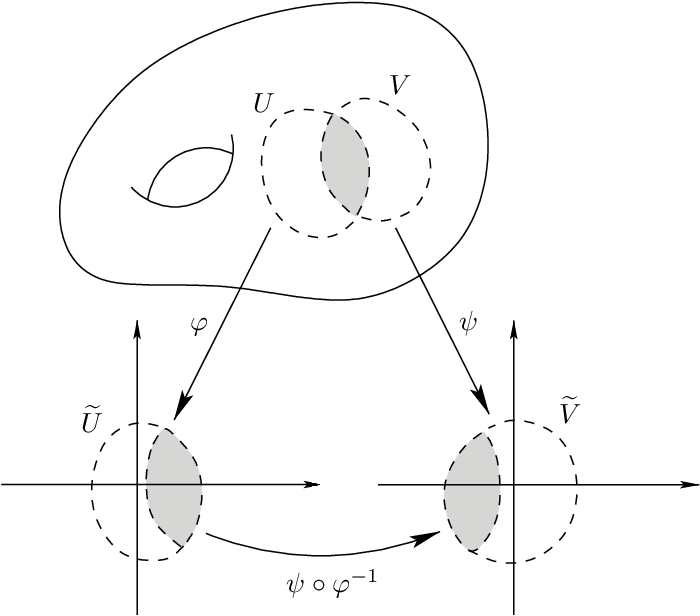
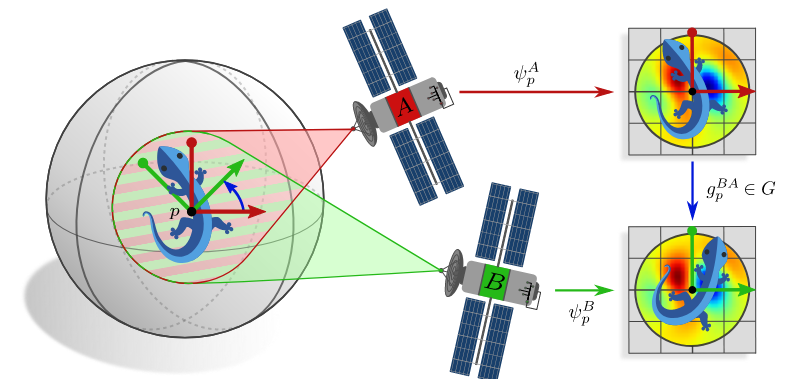
Charts and Atlases
Coordinate chart: An open set (sufficiently small neighborhood) \(U\subseteq\mathcal{M}\) with a homeomorphism \(\psi\)
Atlas: A collection of charts that cover \(\mathcal{M}\)
Transition Map: How to move from one chart to another
Introduction to Smooth Manifolds, Lee
Smooth Manifolds
A manifold is smooth if its atlas has smooth transition maps
Intuition: no corners or edges
Can have different levels of smoothness (\(n\)-times continuously-differentiable vs analytic)
In Topology, When Are Two Shapes the Same?, Hartnett
Derivatives and Integrals
We can compute directional derivatives for functions
We can take integrals of functions, vector fields, etc.
Interesting, but not relevant for the current project
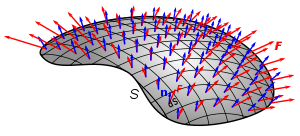
The Tangent Space

Given a point \(x\in M\), we can consider the velocity of curves that pass through \(x\)
This forms a vector space \(T_xM\), called the tangent space
Maps Between Manifolds
Let \(M\) and \(N\) be two manifolds, and \(\phi:M\to N\) a smooth function
We can use \(\phi\) to "move information" between \(M\) and \(N\)
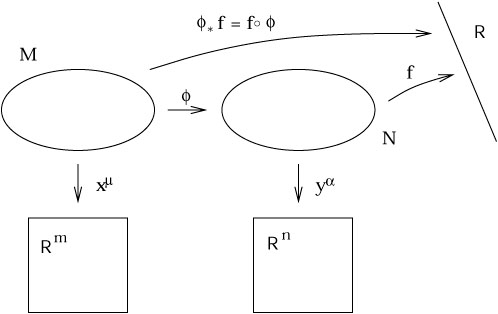
Pushforward
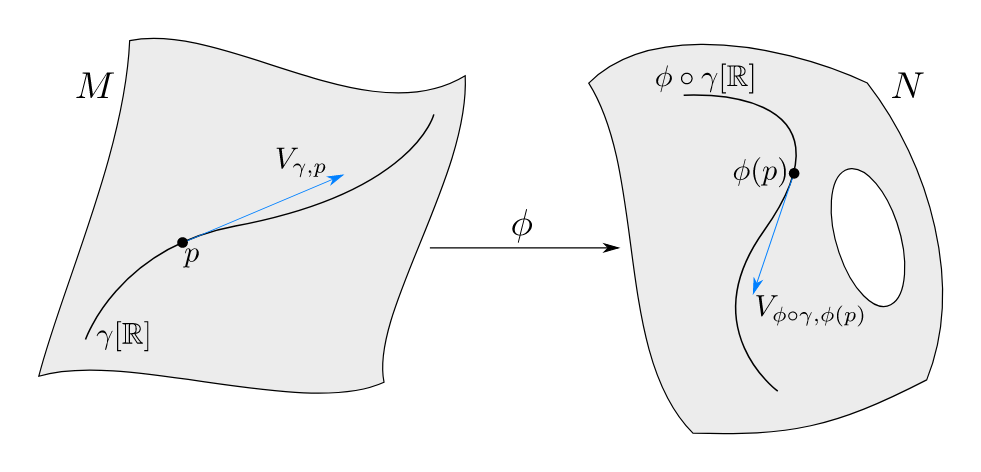
The pushforward \(d\phi\) moves tangent vectors from \(M\) to \(N\)
Pullback

The pullback \(\phi^*\) moves functions from \(N\) to \(M\)
\(\phi^*f=f\circ\phi\)
Application: RMPs
Riemannian Motion Policies use pushforwards and pullbacks to unify controllers across different configuration spaces
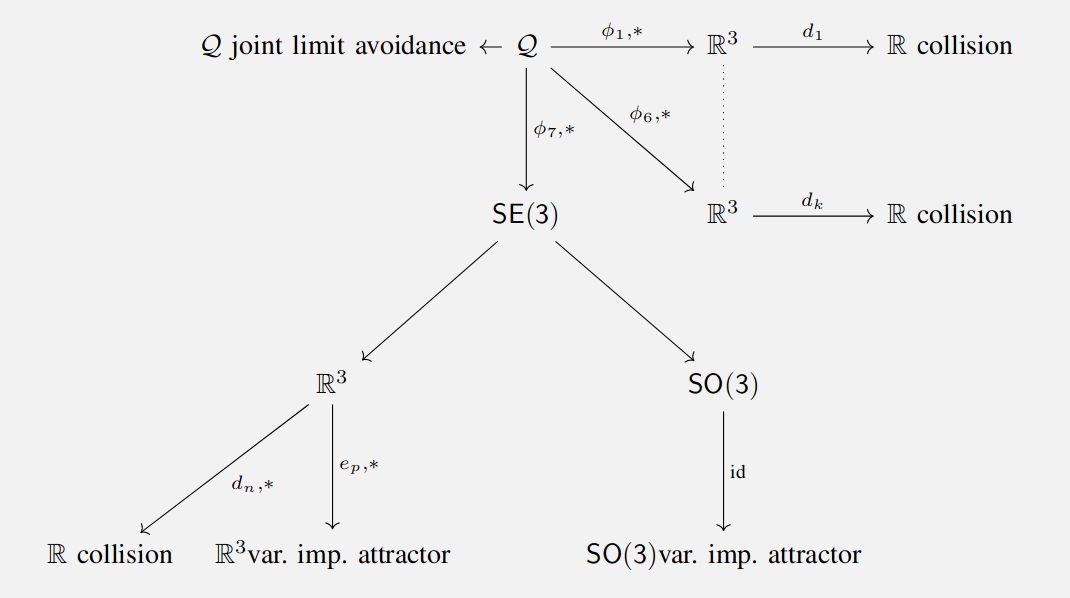
RMPs for Safe Impedance Control in Contact-Rich Maniuplation, Shaw et. al.
Product Manifolds
The Cartesian product of two manifolds is itself a manifold
Lie Groups
What if a manifold is also a group?
Need the group operation and inversion to be smooth maps
Examples: SO(3), SE(3)
Coordiante Independent Convolutional Networks -- Isometry and Gauge Equivariant Convolutions on Riemannian Manifolds, Weiler et. al.
Riemannian Manifolds

Top 5 different world map projections you need to know about, Leitao
Motivation: Distance
Arc length depends on the parameterization of the charts


Motivation: Curvature
Triangles and angles look different
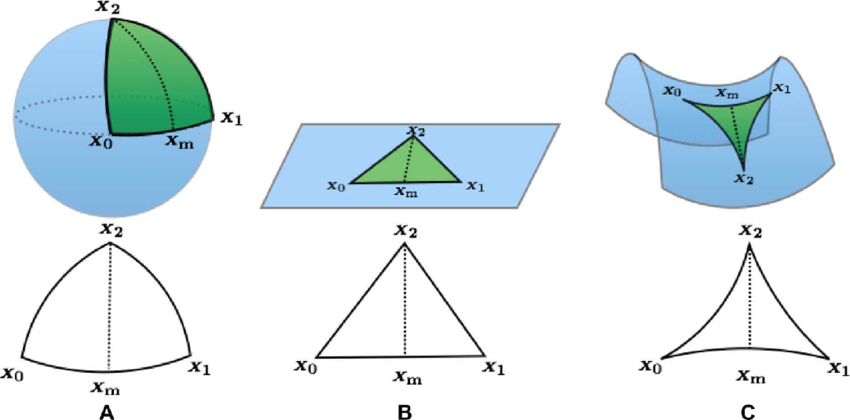
Ricci curvature: An economic indicator for market fragility and systemic risk, Sandhu et. al.
Riemannian Metric
A Riemannian Metric assigns an inner product to each tangent space
The inner product must be a positive definite bilinear form, and it must vary smoothly along the manifold
Allows us to define curvature, and compute distances
Curvature
- Describes how the local geometry differs from Euclidean
- Explicitly, a fourth-order tensor (with complex symmetries)
- Intuition: what do angles and triangles look like?

Ricci curvature: An economic indicator for market fragility and systemic risk, Sandhu et. al.
Arc Length
Consider a piecewise-differentiable curve \(\gamma\in\mathcal{C}^{1}_{\operatorname{pw}}([a,b],\mathcal{M})\)
Its arc length is \(\displaystyle L(\gamma)=\int_a^b \sqrt{\left<\gamma'(s),\gamma'(s)\right>^{\mathcal{M}}_{\gamma(s)}}\,ds\)
For any two points \(p,q\in\mathcal{M}\), the distance between them is defined to be
\[\inf\{L(\gamma)\,|\,\gamma\in\mathcal{C}^{1}_{\operatorname{pw}}([0,1],\mathcal{M}),\gamma(0)=p,\gamma(1)=q\}\]
This integral is parameterization-independent
Geodesics
A geodesic is a (locally) length-minimizing curve -- solution to
\[\operatorname{arg}\,\inf\{L(\gamma)\,|\,\gamma\in\mathcal{C}^{1}_{\operatorname{pw}}([0,1],\mathcal{M}),\gamma(0)=p,\gamma(1)=q\}\]
Variational calculus problem -- solution satisfies Euler-Lagrange system of differential equations
As a result, each geodesic is uniquely defined by its initial conditions
Computation: forward integrate the differential equations
Examples of Geodesics
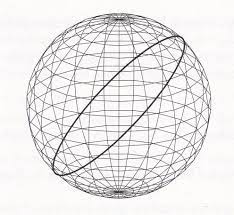
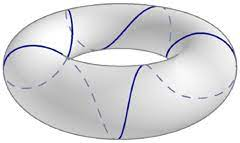
Geodesics on Surfaces by Variational Calculus, Villanueva
The Curvature and Geodesics of the Torus, Irons
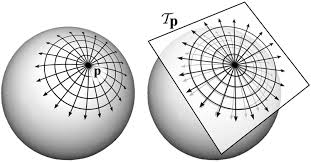
Exponential Map
Tangent vectors are velocities of curves through a point
Exponential map intuition:
- Can extend a tangent vector to a geodesic
- Length of the vector corresponds to distance along the geodesic
- Yields a coordinate chart, called the "normal" coordinates
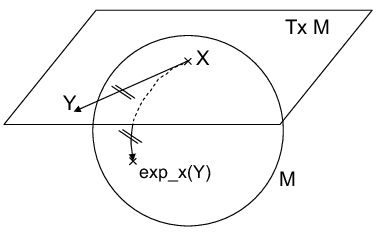
Covariance clustering on Riemannian manifolds for acoustic model compression, Shinohara et. al.
Efficient Computation of Smoothed Exponential Maps, Herholz et. al.
Part 3
Motion Planning in Non-Euclidean Spaces
Problem Statement
Configuration space \(\mathcal{Q}\) as a Riemannian manifold
\(\mathcal{M}\subseteq\mathcal{Q}\) is the set of collision free configurations, \(\bar{\mathcal{M}}\) its closure
The shortest path between \(p,q\in\bar{\mathcal{M}}\) is the solution to the optimization problem
\[\begin{array}{rl} \argmin & L(\gamma)\\ \textrm{subject to} & \gamma\in\mathcal{C}^{1}_{\operatorname{pw}}([0,1],\bar{\mathcal{M}})\\ & \gamma(0)=p\\ & \gamma(1)=q\end{array}\]
The Plan...
- Formulate GCS on a Manifold
- Add Structure to the Problem
- Transform to GCS in Euclidean Space
Geodesic Convexity
- Bring the ideas of convexity to Riemannian manifolds
- Enables optimization with strong guarantees
- Young but growing area of study
Re-visiting Riemannian geometry of symmetric positive definite matrices for the analysis of functional connectivity, You et. al.
Convex Sets
A set \(X\subseteq\mathbb{R}^n\) is convex if \(\forall p,q\in X\), the line connecting \(p\) and \(q\) is contained in \(X\)
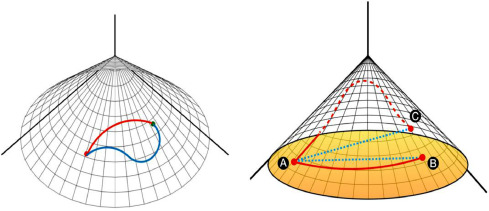
Geodesically Convex Sets
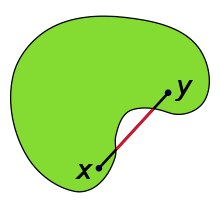
A set \(X\subseteq\mathcal{M}\) is strongly geodesically convex if \(\forall p,q\in X\), there is a unique length-minimizing geodesic (w.r.t. \(\mathcal{M}\)) connecting \(p\) and \(q\), which is completely contained in \(X\).
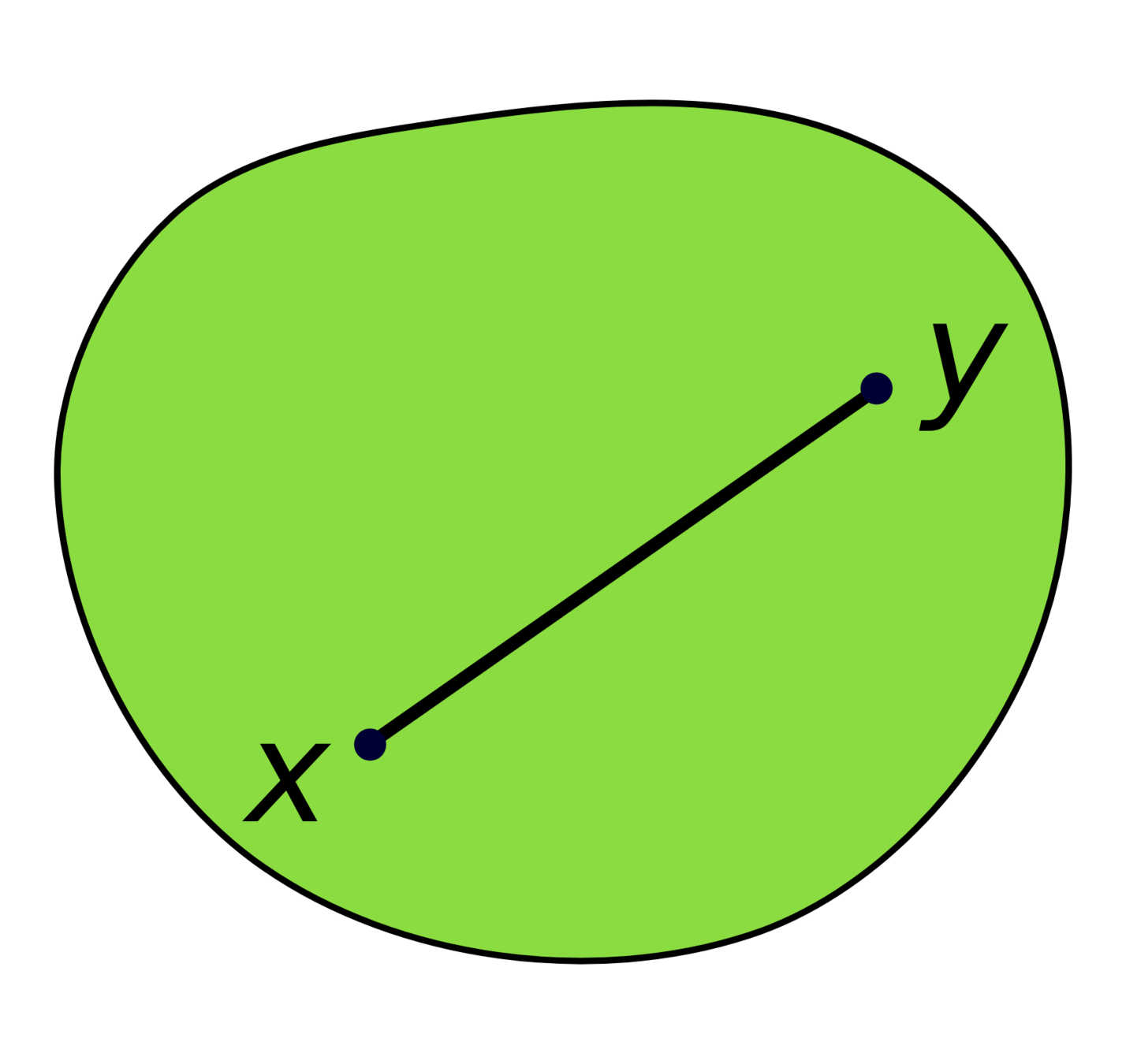
Convex Set, Wikipedia
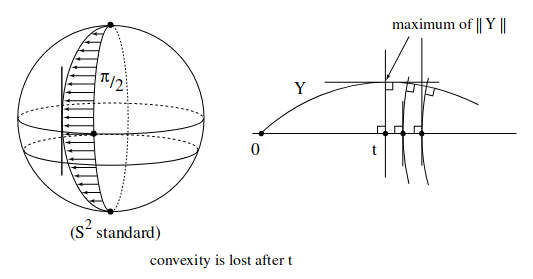
Some Sets Look Convex
(But Aren't)

Sets can be convex in local coordinates, but not geodesically-convex on the manifold
Geodesics can go "the wrong way around"
Radius of convexity: how large can a set be and still be convex?
Which Continent Is Situated In All Four Hemispheres?, Junior
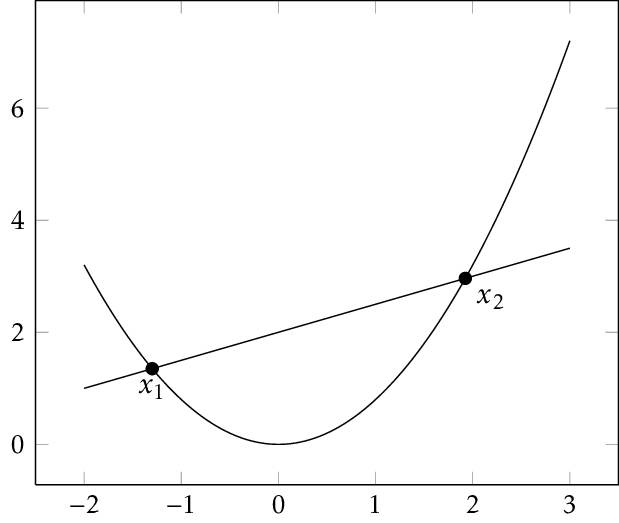
Convex Functions
A function \(f:X\to\mathbb{R}\) is convex if for any \(x,y\in X\) and \(\lambda\in[0,1]\), we have
\(f(\lambda x+(1-\lambda)y)\le\)
\(\lambda f(x)+(1-\lambda) f(y)\)
Geodesically Convex Functions
A function \(f:\mathcal{M}\to\mathbb{R}\) is geodesically convex if for any \(x,y\in \mathcal{M}\) and any geodesic \(\gamma:[0,1]\to\mathcal{M}\) such that \(\gamma(0)=x\) and \(\gamma(1)=y\), \(f\circ\gamma\) is convex
Convex Functions
Geodesically Convex Functions

Geodesics on Surfaces by Variational Calculus, Villanueva
Fighter Aircraft Maneuver Limiting Using MPC - Theory and Application, Simon
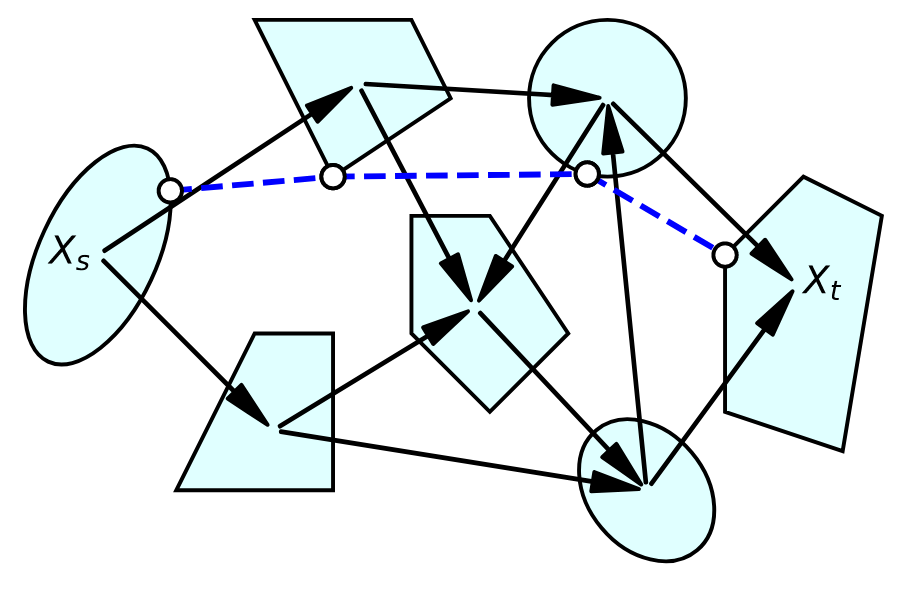
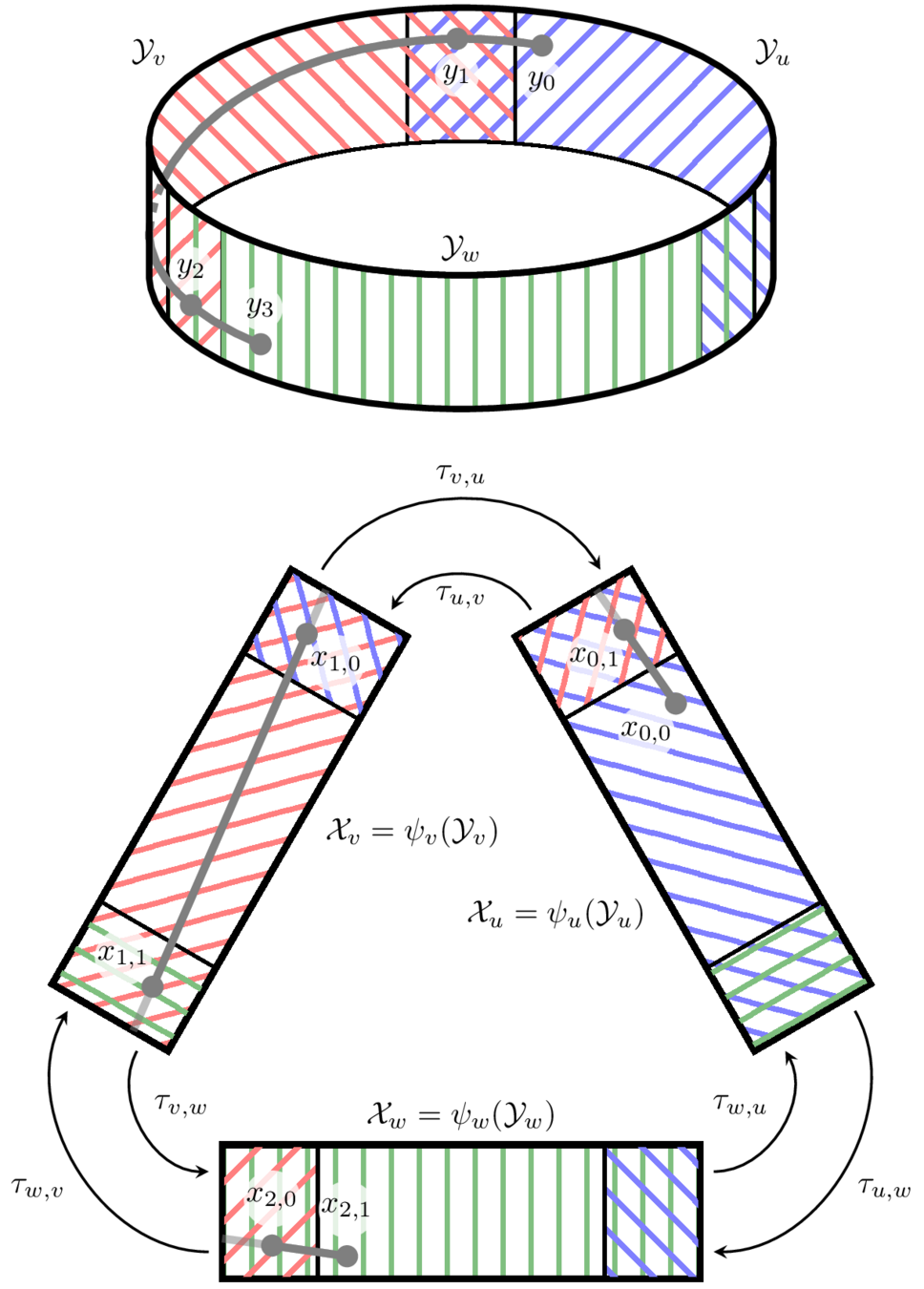
A Graph of Geodesically Convex Sets (GGCS)
A directed graph \(G=(V,E)\)
- For each vertex \(v\in V\), there is a strongly geodesically convex manifold \(\mathcal{Y}_v\)
- For each edge \(e=(u,v)\in E\), there is a cost function \(\ell_e^\mathcal{Y}:\mathcal{Y}_u\times\mathcal{Y}_v\to\mathbb{R}\)
- \(\ell_e^\mathcal{Y}\) must be geodesically convex with respect to the product metric on \(\mathcal{Y}_u\times\mathcal{Y}_v\)
GCS

GGCS

Shortest Paths in GGCS
Mixed-Integer Riemannian Optimization? No existing literature.
Better option: transform into a GCS problem
Pullback of Sets and Edges
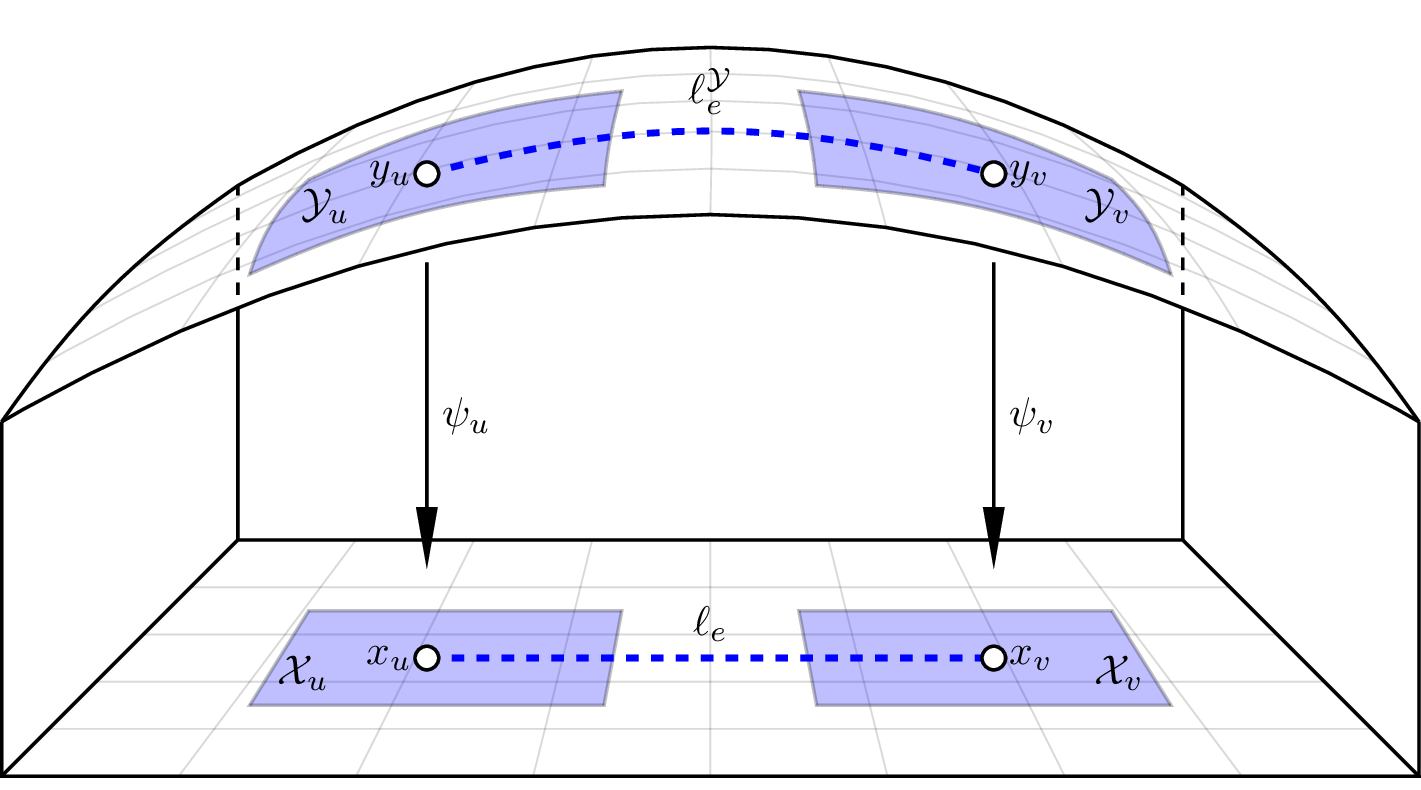
Shortest Paths in GGCS
For each \(v\in V\), let \(\psi_v:\mathcal{Y}_v\to\mathbb{R}^n\) be a coordinate chart
Define \(X_v=\psi_v(\mathcal{Y}_v)\)
For each \(e=(u,v)\in E\), new edge cost:
\[\ell_e(x_u,x_v)=\ell_e^\mathcal{Y}(\psi_u^{-1}(x_u),\psi_v^{-1}(x_v))\]
If all \(X_v\) and \(\ell_e\) are convex, we have a valid GCS problem
Mixed-Integer Riemannian Optimization? No existing literature.
Better option: transform into a GCS problem
Problem Statement
Configuration space \(\mathcal{Q}\) as a Riemannian manifold
\(\mathcal{M}\subseteq\mathcal{Q}\) is the set of collision free configurations, \(\bar{\mathcal{M}}\) its closure
The shortest path between \(p,q\in\bar{\mathcal{M}}\) is the solution to the optimization problem
\[\begin{array}{rl} \argmin & L(\gamma)\\ \textrm{subject to} & \gamma\in\mathcal{C}^{1}_{\operatorname{pw}}([0,1],\bar{\mathcal{M}})\\ & \gamma(0)=p\\ & \gamma(1)=q\end{array}\]
Additional Requirements
\(\mathcal{Q}\) is zero-curvature
- Negative-curvature manifolds not common in robotics
- Distance metric on positive curvatures is nonconvex 😡

Ricci curvature: An economic indicator for market fragility and systemic risk, Sandhu et. al.
Zero-Curvature is Still Useful
- All 1-dimensional manifolds
- Continuous revolute joints
- \(\operatorname{SO}(2)\), \(\operatorname{SE}(2)\)
- Products of flat manifolds
Fetch Robot Configuration
Space: \(\operatorname{SE}(2)\times \mathbb{T}^3\times \mathbb{R}^7\)

Trajectory Control for Differential Drive Mobile Manipulators, Karunakaran et. al.
Additional Requirements
\(\mathcal{Q}\) is zero-curvature
- Negative-curvature manifolds not common in robotics
- Distance metric on positive curvatures is nonconvex
\(\mathcal{A}=\{(X_v,\psi_v)\}_{v\in V}\) is a finite atlas of \(\mathcal{M}\), with each \(X_v\) strongly geodesically convex, and each \(\psi_v\) an isometry
- Necessary for computation
- Leads to nice theoretical results
Reminder: Transition Maps
How to move from one chart to another
Introduction to Smooth Manifolds, Lee

Reformulating as GCS
Decision variables:
\(\forall v\in V\), we have \(x_v=(x_{v,0},x_{v,1})\in\psi_v(X_v)^2\)
Edge costs:
\[\ell_e(x_u,x_v)=||x_{u,0}-x_{u,1}||_2,\quad\forall e=(u,v)\in E\]
Edge constraints:
\[\tau_{u,v}(x_{u,1})=x_{v,0},\quad\forall e=(u,v)\in E\]
(\(\tau_{u,v}\) is the transition map from \(X_u\) to \(X_v\))
Motion Planning around Obstacles with Convex Optimization, Marcucci et. al.
Reformulating as GCS
Decision variables:
\(\forall v\in V\), we have \(x_v=(x_{v,0},x_{v,1})\in\psi_v(X_v)^2\)
Edge costs:
\[\ell_e(x_u,x_v)=||x_{u,0}-x_{u,1}||_2,\quad\forall e=(u,v)\in E\]
Edge constraints:
\[\tau_{u,v}(x_{u,1})=x_{v,0},\quad\forall e=(u,v)\in E\]
(\(\tau_{u,v}\) is the transition map from \(X_u\) to \(X_v\))
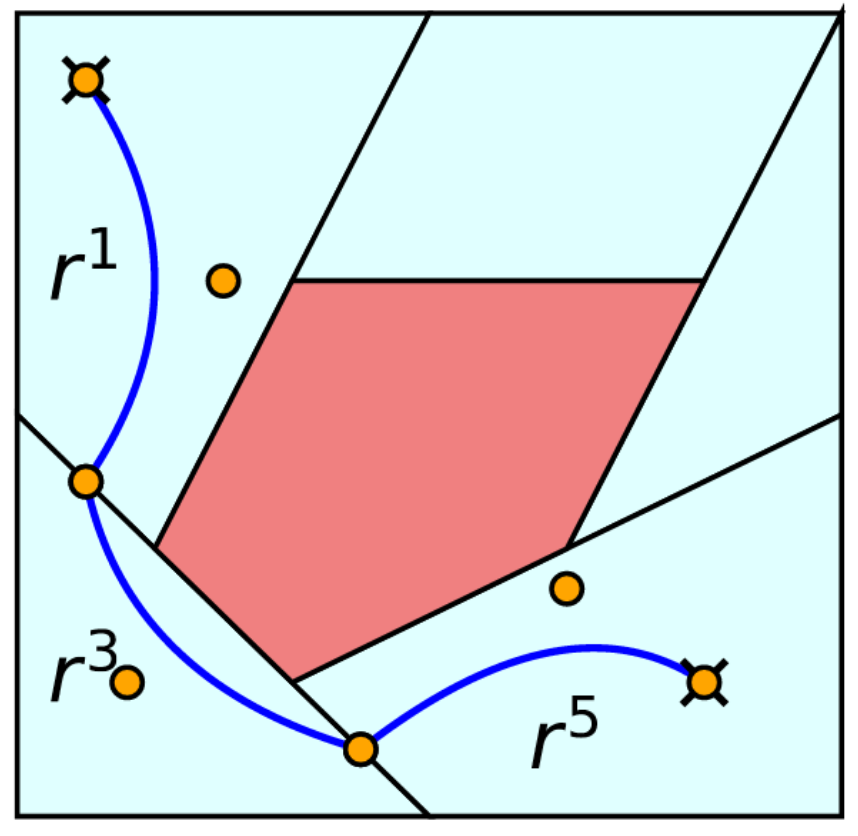
Nice Theoretical Results?
- There is a shortest path \(\gamma\) connecting \(p\) to \(q\) through \(\bar{\mathcal{M}}\) such that
- \(\gamma\) is piecewise geodesic
- Each geodesic segment is contained in some \(\bar{\mathcal{Y}}_u\)
- \(\gamma\) passes through each \(\bar{\mathcal{Y}}_u\) at most once
-
Ensures that a shortest path is feasible for GGCS
- Transition maps are affine functions (in particular, they are an orthogonal transformation plus a translation)
- Formal equivalence of GGCS and transformed GCS problem
Part 4
Results
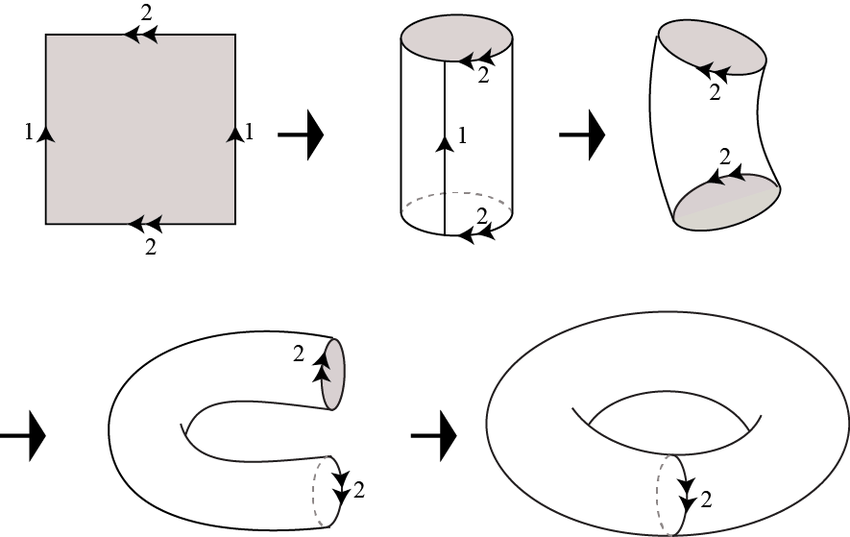
"Asteroids" World
Square with opposite edges identified
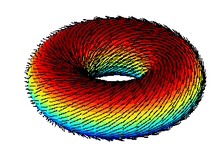
Configuration Space: \(\mathbb{T}^2\)
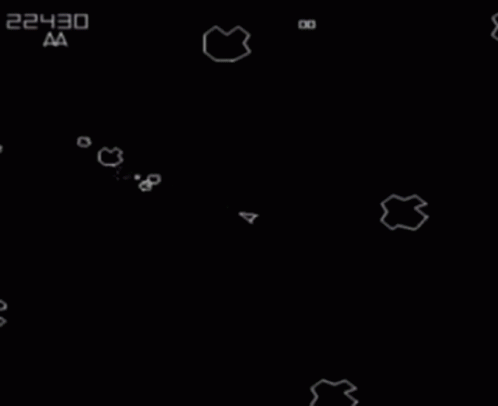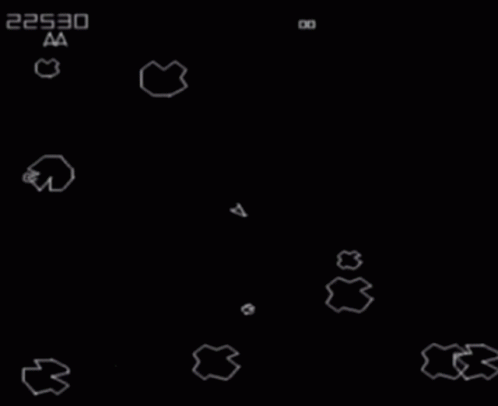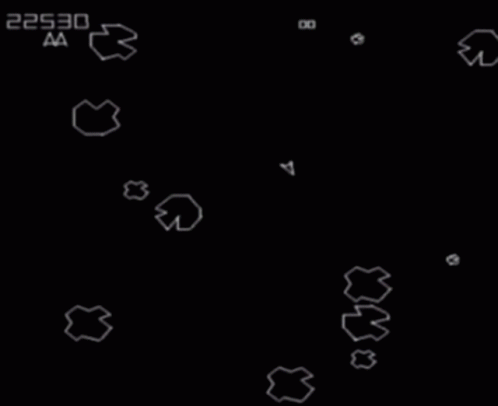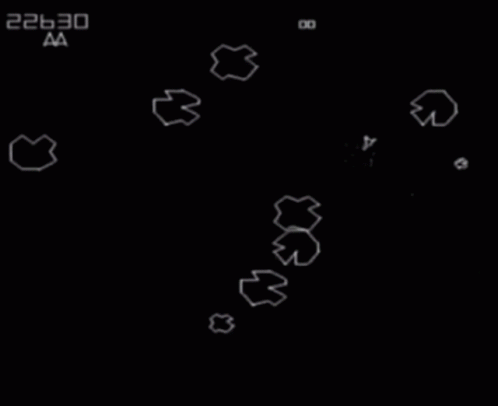
Planar Arm
A robot arm with 5 continuous revolute joints in the plane
Configuration Space: \(\mathbb{T}^5\)
(No self collisions)

(Modified) Kuka iiwa Arm
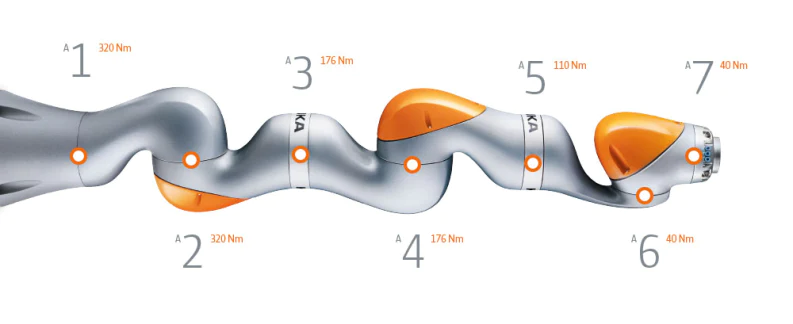
Modified to be a continuous revolute joint
PR2 Whole Body Plans

Robot Operating System (ROS), Picknik
Comparison: PRM + TrajOpt
- Build an initial plan with a PRM
- Post-process with kinematic trajectory optimization
More Results
ggcs-anonymous-submission.github.io
Practicum
Generating Atlases
Key idea: generate within a chart in the first place
Use IRIS in configuration space, add bounds on the diameter of the set to preserve strong convexity
A Panoramic View of Riemannian Geometry, Berger
Further Motion Planning
All Bézier curve constructions also hold on the manifold
For higher-order continuity constraints, want tangent vectors to be equal. Use the pushforward!

Higher Order Continuity
Order \(0\) continuity, order \(k\) splines:
\[\tau_{u,v}(x_{u,k})=x_{v,0}\quad\forall e=(u,v)\in E\]
Order \(m\) continuity, order \(k\) splines:
\[(\tau_{u,v})_*(x^{(m)}_{u,k})=x^{(m)}_{v,0}\quad\forall e=(u,v)\in E\]
If \(\tau_{u,v}\) is an isometry, it's just a rotation plus a translation.
So then \((\tau_{u,v})_*\) is just a rotation
Globally-Aligned Coordinates
In some (most?) cases, we can align the coordinate systems
If so, we have \(\tau_{u,v}\in \operatorname{T}(n)\) and \((\tau_{u,v})_*=I_n\), \(\forall e=(u,v)\in E\)
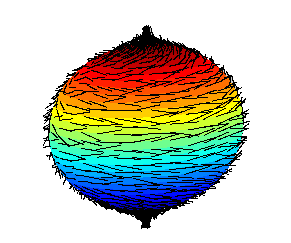
Part 5
Next Steps and Future Directions
GGCS
Piecewise Linear Approximation
Bimanual Manipulation with Analytic Inverse Kinematics
Nonlinear Continuation for General Implicit Constraints
Multifario, Henderson
GCS in General
Tobia: Large Scale Planning
David: Handling Nonconvexities
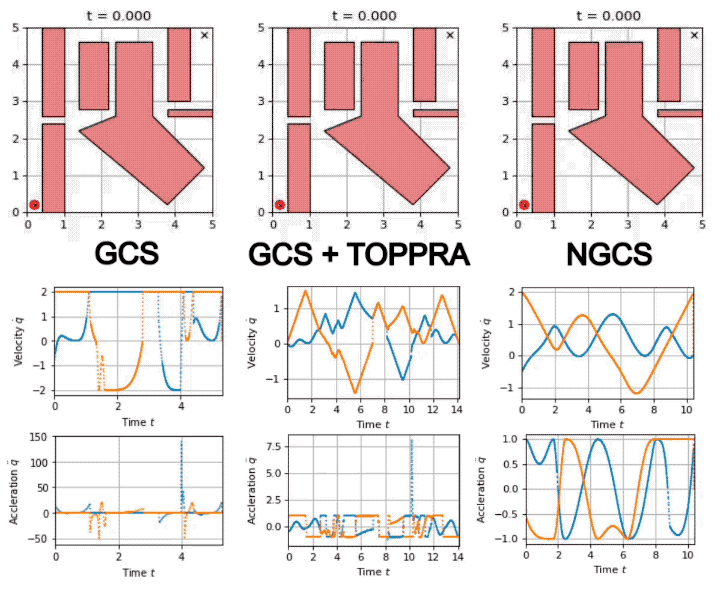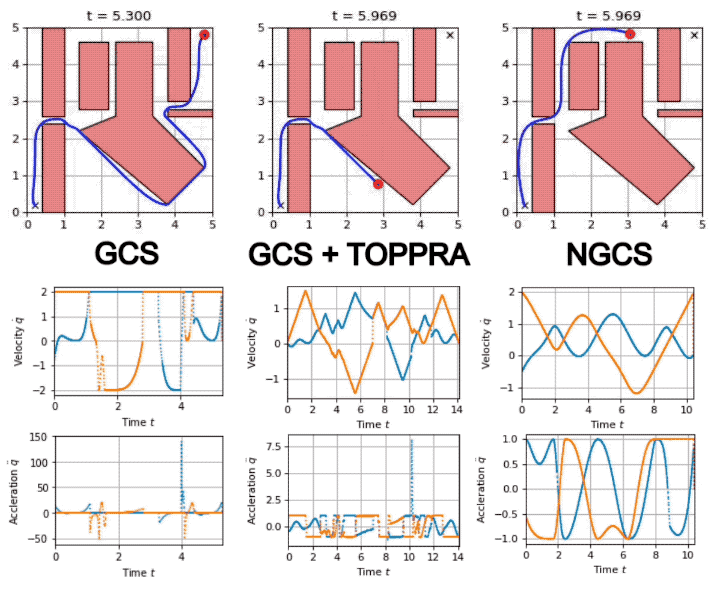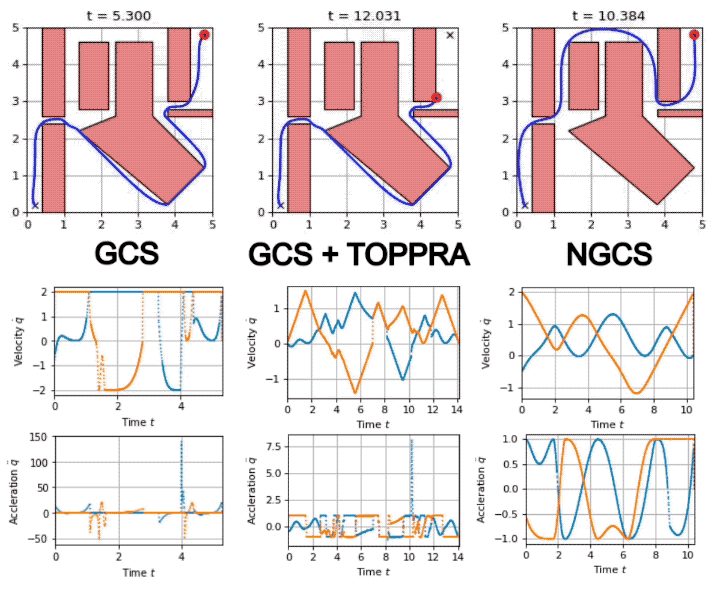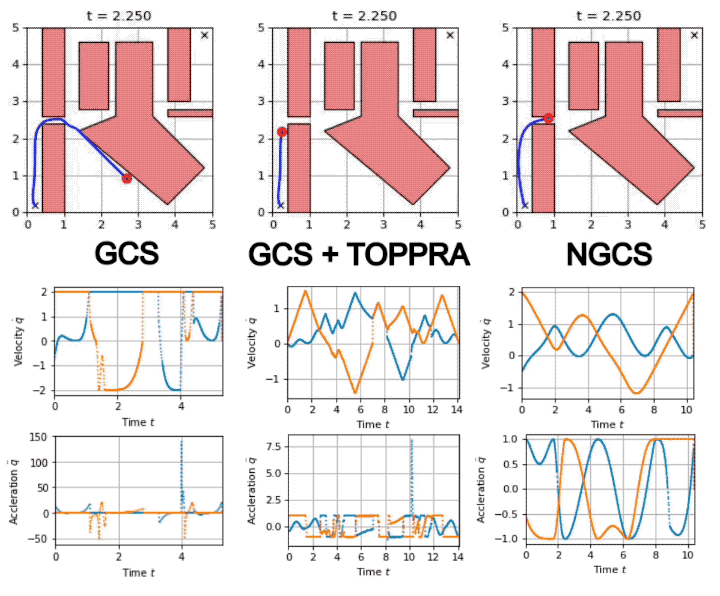
Savva: GCS as a Policy
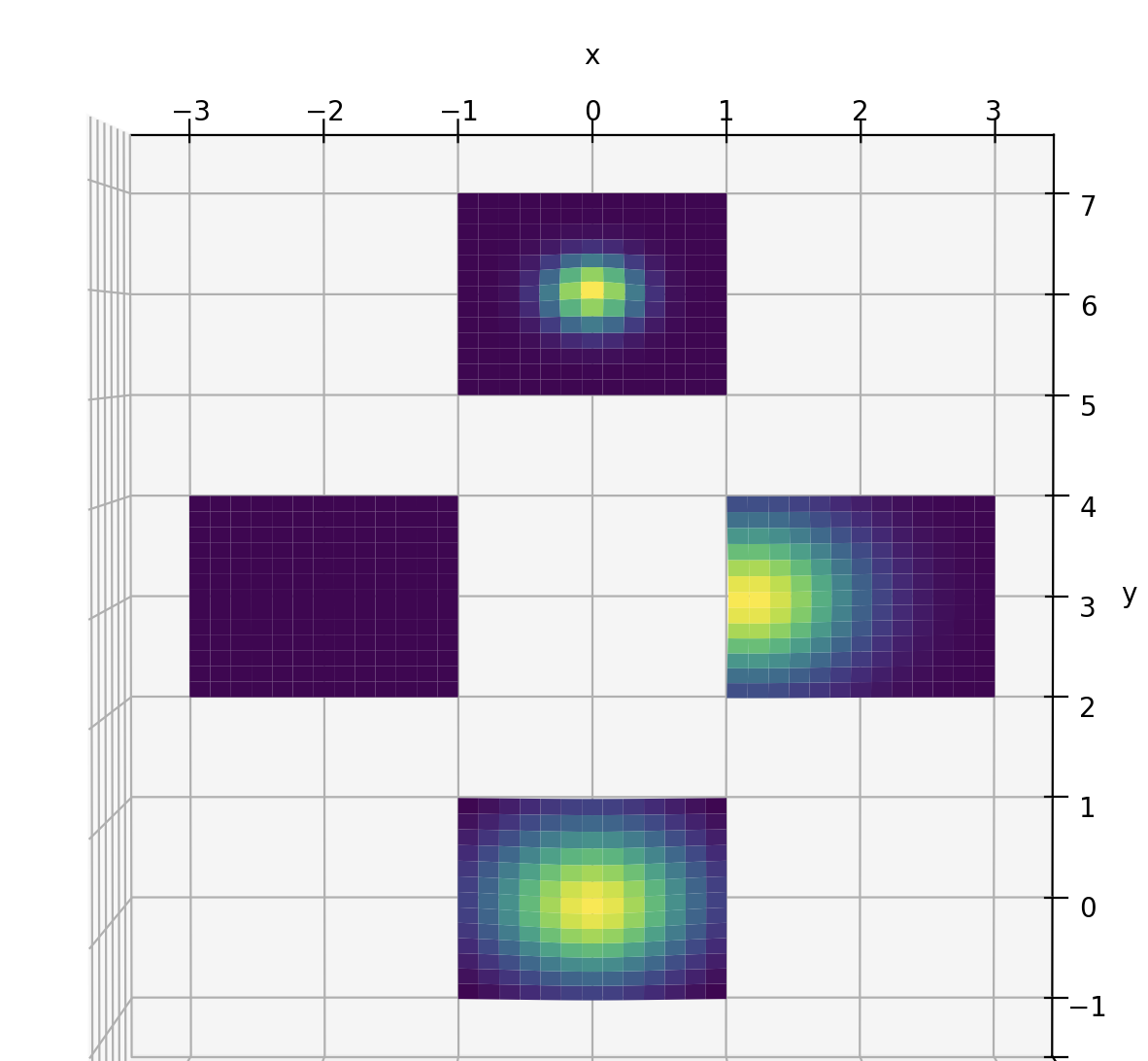
Bernhard: Contact Rich Planning
Non-Euclidean Motion Planning with Graphs of Geodesically-Convex Sets

Thomas Cohn, Mark Petersen, Max Simchowitz, Russ Tedrake

June 9, 2023