GGCS RSS Talk

Non-Euclidean Motion Planning with Graphs of Geodesically-Convex Sets

Thomas Cohn, Mark Petersen, Max Simchowitz, Russ Tedrake

Motion Planning Today

Sampling-based planning
- ```
+
```
  Global (probabilistic) completeness
- ```
-
```
  "Curse of Dimensionality"
- ```
-
```
  Non-smooth paths
Trajectory optimization
- ```
-
```
  Nonconvex
- ```
+
```
  Scales with dimension
- ```
+
```
  Smooth paths, dynamics

Motion Planning, Wikipedia

Motion Planning Today

Sampling-based planning
- ```
+
```
  Global ~~(probabilistic)~~ completeness
- ```
-
```
  "Curse of Dimensionality"
- ```
-
```
  Non-smooth paths
Trajectory optimization
- ```
-
```
  Nonconvex
- ```
+
```
  Scales with dimension
- ```
+
```
  Smooth paths, dynamics

Common challenge: collision avoidance

Motion Planning, Wikipedia

Sampling-based planning
- ```
+
```
  Global (probabilistic) completeness
- ```
-
```
  "Curse of Dimensionality"
- ```
-
```
  Non-smooth paths
Trajectory optimization
- ```
-
```
  Nonconvex
- ```
+
```
  Scales with dimension
- ```
+
```
  Smooth paths, dynamics

Planning through Convex Sets

Motion Planning around Convex Obstacles with Convex Optimization, Marcucci et. al.

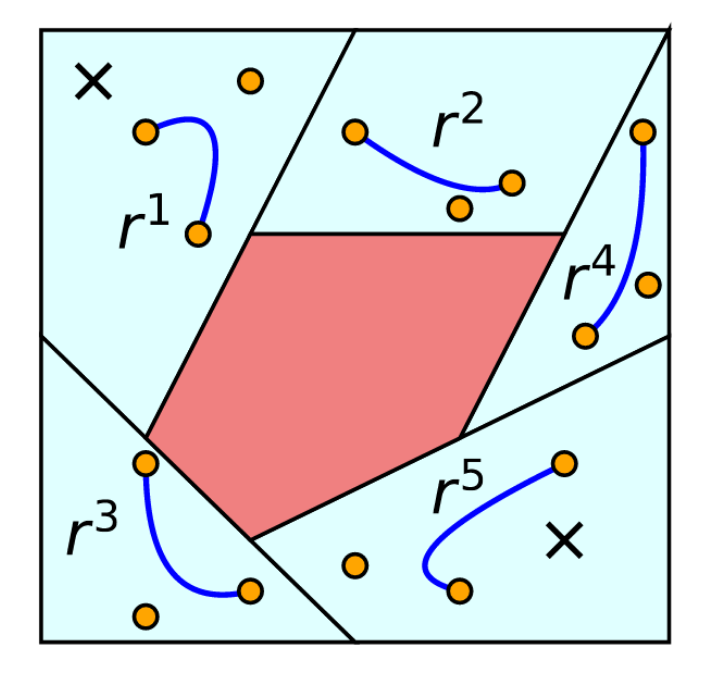
Obstacle avoidance: nonconvex

Safe-set containment: convex

Obstacle avoidance guarantees!

Piecewise-linear trajectories: just check endpoints
Bezier curves: check control points

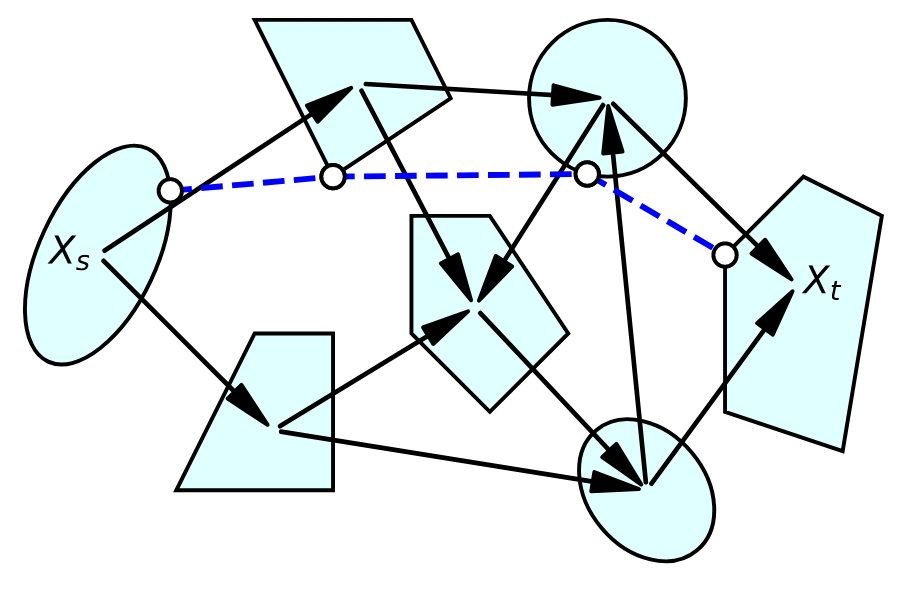
Motion Planning with GCS

Represent C-Free with convex sets
Formulate shortest path problem as MICP
Can solve to optimality (branch and bound)
In practice, relax and round yields a good result

Shortest Paths in Graphs of Convex Sets, Marcucci et. al.

Motion Planning around Convex Obstacles with Convex Optimization, Marcucci et. al.

What about non-Euclidean configuration spaces?

Configuration Space as a Manifold

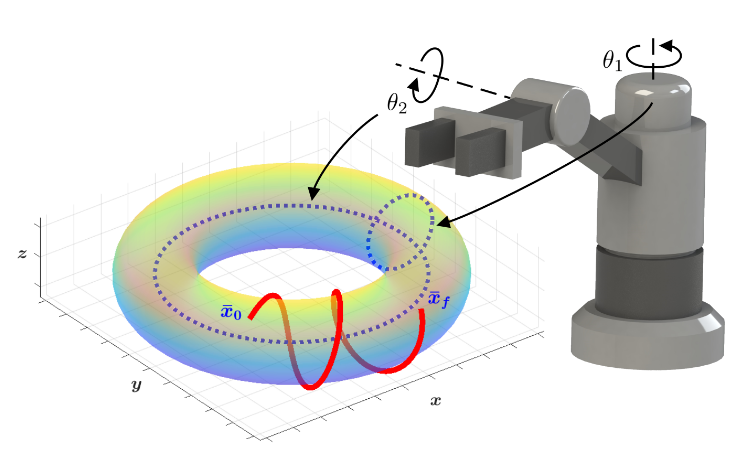
Trajectory Optimization on Manifolds: A Theoretically-Guaranteed Embedded Sequential Convex Programming Approach, Bonalli et. al.

Configuration Space as a Manifold

Trajectory Optimization on Manifolds: A Theoretically-Guaranteed Embedded Sequential Convex Programming Approach, Bonalli et. al.

\(\mathcal{Q}\)

Configuration Space as a Manifold

Trajectory Optimization on Manifolds: A Theoretically-Guaranteed Embedded Sequential Convex Programming Approach, Bonalli et. al.

\(\mathcal{Q}\)

\(\overline{\mathcal{M}}\subseteq\mathcal{Q}\)

(Collision free subset)

Shortest-Path Planning along a Manifold

Trajectory Optimization on Manifolds: A Theoretically-Guaranteed Embedded Sequential Convex Programming Approach, Bonalli et. al.

\[\begin{array}{rl} \argmin & L(\gamma)\\ \textrm{subject to} & \gamma\in\mathcal{C}^{1}_{\operatorname{pw}}([0,1],\overline{\mathcal{M}})\\ & \gamma(0)=p\\ & \gamma(1)=q\end{array}\]

Shortest-Path Planning along a Manifold

\[\begin{array}{rl} \argmin & L(\gamma)\\ \textrm{subject to} & \gamma\in\mathcal{C}^{1}_{\operatorname{pw}}([0,1],\bar{\mathcal{M}})\\ & \gamma(0)=p\\ & \gamma(1)=q\end{array}\]

Minimize arc length

Path must be

piecewise-differentiable

Start at point \(p\)

Finish at point \(q\)

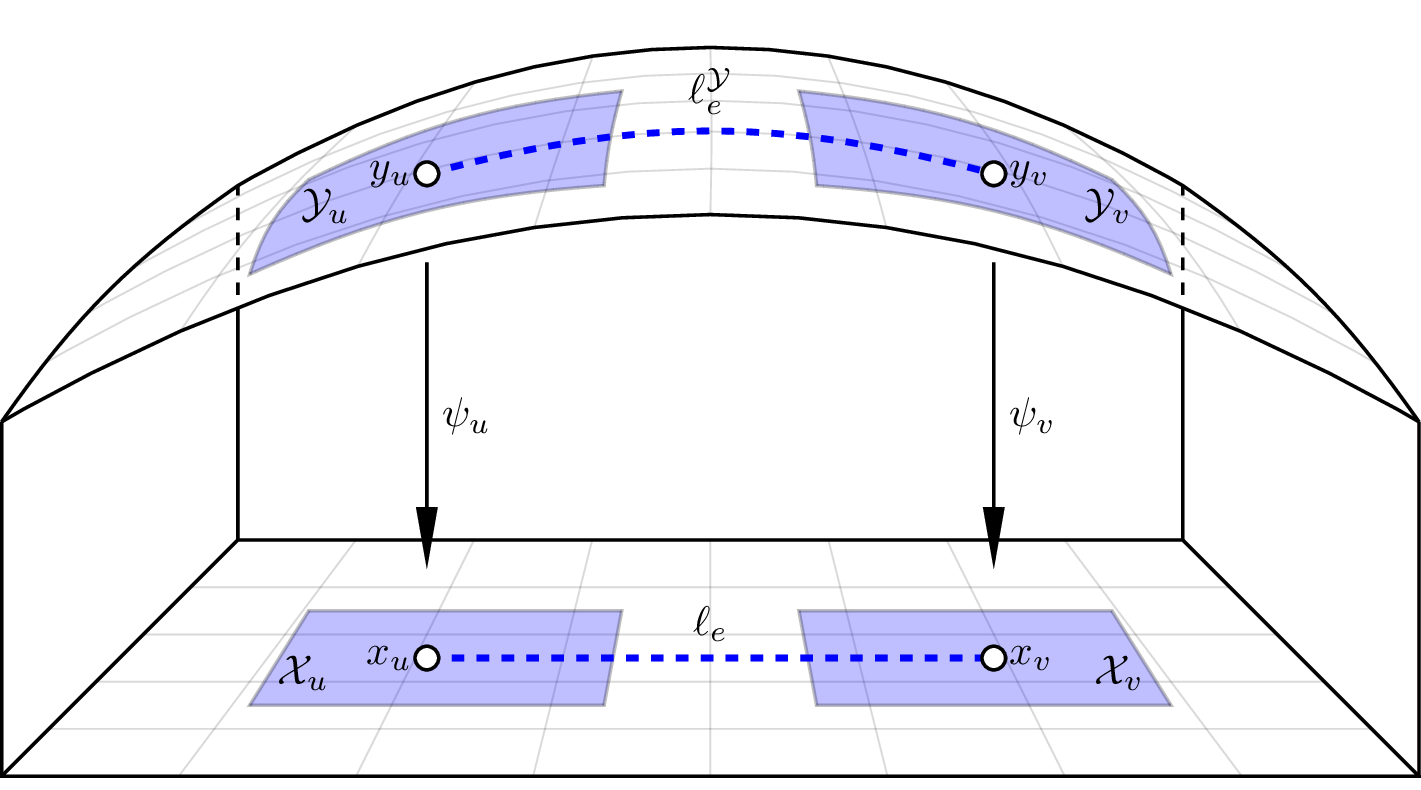
Computing Shortest Paths

Formulate GCS on a Manifold
Transform Problem back into Euclidean Space
Additional requirements to ensure convexity

Results: PR2 Whole-Body Plans

Robot Operating System (ROS), Picknik