Inverse Dynamics Control through Optimization-Based Dynamics
Terry
2023/09/15
Today's Topic
How should we be thinking about local feedback control for manipulation?
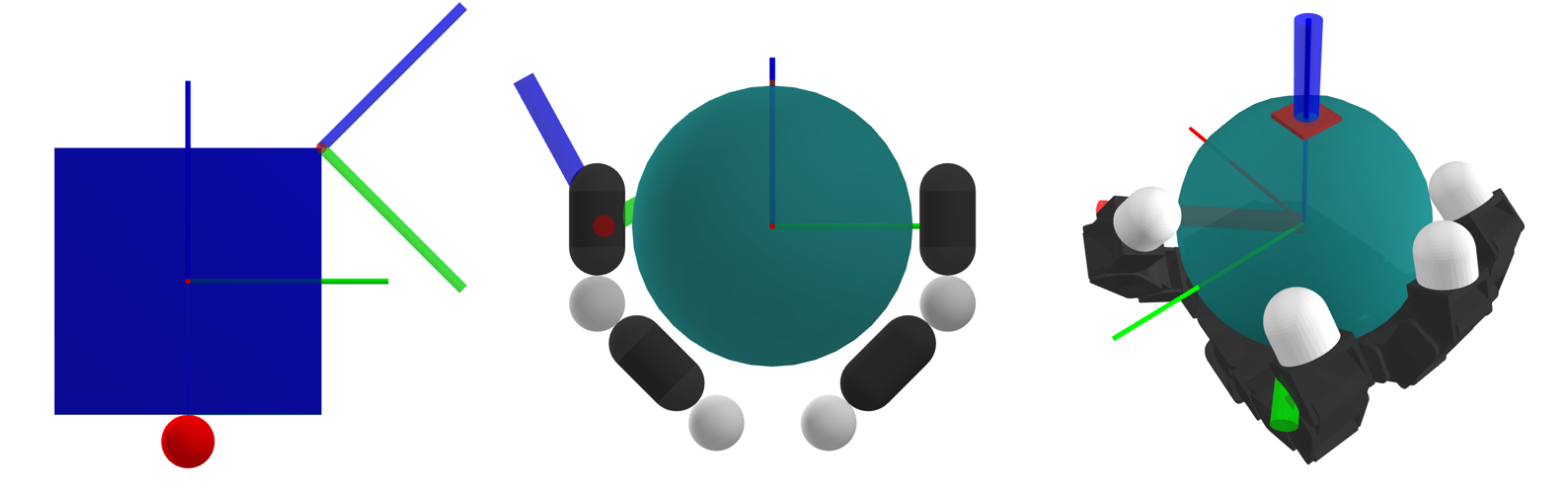
Inverse Dynamics
Inverse Dynamics as Local Control
Forward Dynamics
Inverse Dynamics
Inverse Dynamics Control for Smooth Systems
Given a desired acceleration of the robot, and the current state (joint state + velocities + contact forces), which torque should I apply to the robot?
Inverse Dynamics: Short comings
Inverse Dynamics Control for Smooth Systems
Given a desired acceleration of the robot, the current state, and the contact Jacobian (joint state + velocities), which torque should I apply to the robot?
Shortcomings
Only considers a fixed contact mode, and the controller no longer reasons about change of contact sequences during local control.
Okay for stabilizing locomotion (two feet are always on the ground), but spells trouble for manipulation!
How can we do better?
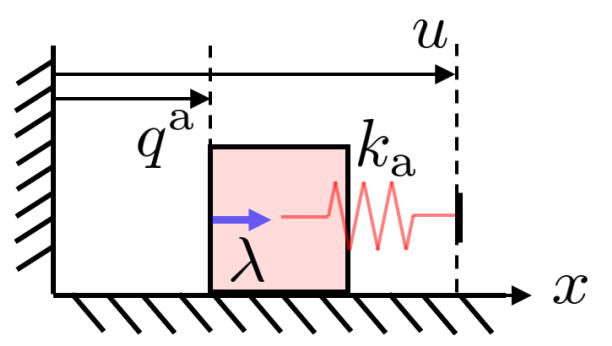
Background: Contact Dynamics
Momentum-Impulse on Object
Impulse Balance on Robot Impedance
Contact Forces can only push, but not pull
Linearized Non-Penetration
Complementarity
Actuated
Unactuated
Background: Contact Dynamics
Dynamics Problem
Equivalent optimization problem
"Find me a minimum work configuration while respecting non-penetration."
Background Contact Dynamics
Optimal solution to the unconstrained problem:
Position command is exactly obeyed
If this solution meets constraints, then this is the optimal solution.
If not, optimality happens right at the boundary of the constraint.
Optimal Control with Contact Dynamics
What we care about is optimizing for some parameters of an optimal control problem.
We will take one-step trajectory optimization as an example.
But this is difficult because f describes an optimal solution to an optimization problem!
Bi-level Optimization
Optimal Control with Contact Dynamics
KKT Reformulation Approach
Sensitivity Analysis Approach
Bi-level Optimization
Two approaches to tackling these in general.
Solvers hate the nonconvexity from complementarity.
Two approaches to tackling these in general.
If we have the gradients
through sensitivity analysis of the inner optimization problem, then possible to plug this into iterative solvers.
Sensitivity Analysis
What do gradients do? They allow us to construct a locally linear model around the current iterate.
We had used this sensitivity extensively in previous projects.
1. This is a linearization of the dynamics, allows us to tools such as iLQR.
2. Linearization also allows us to approximate reachability effectively.
Inverse Dynamics Interpretation
If we strictly enforce the goal displacement, we obtain inverse dynamics from locomotion.
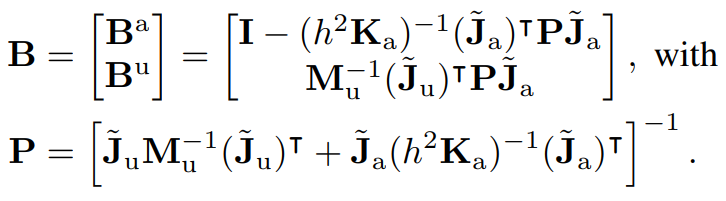
Note that B is highly abstracted out here, but actually corresponds to a lot of Jacobian computations.
It answers queries of "if I think of active contacts as a joint, how does my actuator torques affect forces onto the configuration of the object locally?"
Shortcomings of Linearization
Current position
No Gradient information!
If the object is not in contact, traditional inverse dynamics is not effective.
Fortunately, smoothing comes to the rescue.
rho subscript denotes smoothing
Shortcomings of Linearization
0.5m
0.0m
We have linearized the smoothened dynamics around u = qa.
Depending on where we set the goal to be, we see three distinct regions.
rho subscript denotes smoothing
Shortcomings of Linearization

0.5m
0.0m
Region 1. Beneficial Bias
Goal = 0.61m
Optimal input
The linearized model provides helpful bias, as the optimal input moves the actuated body towards making contact.
rho subscript denotes smoothing
Shortcomings of Linearization

0.5m
0.0m
Region 2. Hurtful Bias
Goal = 0.52m
Optimal input
If you command the actuated body to hold position, the unactuated body will be pushed away due to smoothing.
The actuated body wants to go backwards in order to decrease this effect if the goal is not too in front of the unactuated body.
rho subscript denotes smoothing
Shortcomings of Linearization

0.5m
0.0m
Region 3. Violation of unilateral contact
Goal = 0.45m
Optimal input
If you set the goal to behind the unactuated body, the linear model thinks that it can pull, and will move backwards.
Reachable Set Computation
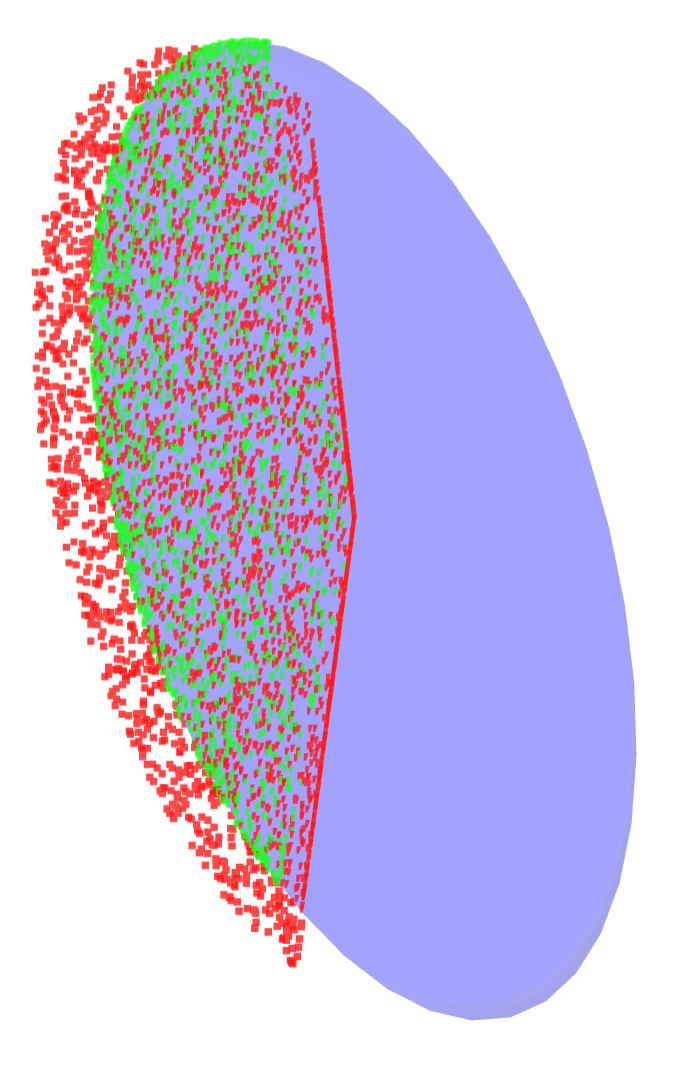
Simulator rollouts of a action norm-ball
Ellipsoid informed by the local B matrix
Similarly, we are horribly off in our approximation of the reachable set constructed from the B matrix.
Clearly we need to think about forces in order to property define reachable sets under linearization
But we don't have contact forces as a decision variable...how?
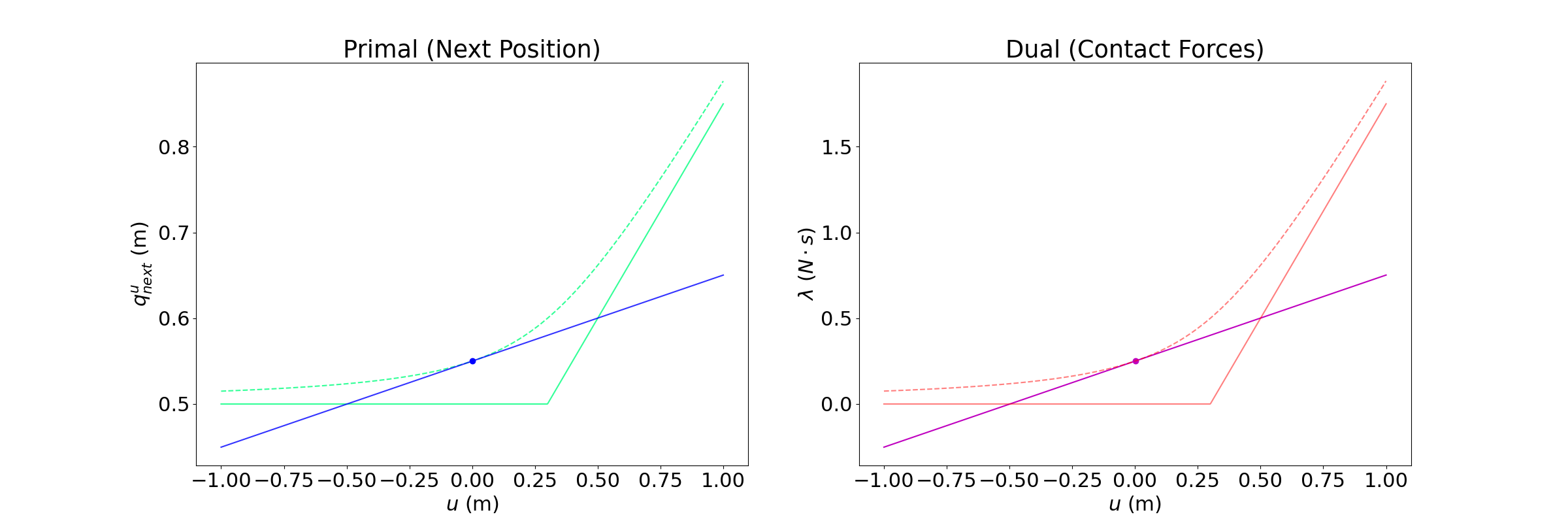
Linearizing an Optimal Solution
What does it mean to create a locally linear model of a solution of an optimization problem?
Generic QP
Generic QP
Linear Model of Primal solution vs. Parameters
Linearizing an Optimal Solution
What does it mean to create a locally linear model for an optimization problem?
Generic QP
Generic QP
Linear Model of Primal solution vs. Parameters
Linear Model of Dual solution vs. Parameters
We can enforce primal and dual feasibility as the domain of the linear model.
New Approach at Linearization

Linearizing the dual and forcing the linear model of the dual to be positive discards the unilateral violation region.
New Approach at Linearization

Interestingly, one solution to getting rid of the hurtful bias region is to keep the slope of the linearization, but make it pass through the non-smooth dynamics.
(e.g. keep the direction, but respect the fact that if no contact will result in no movement)
Applications

- is not limited to limit surfaces ;)
- accounts for non-fixed contact modes
- respects unilateral contact
Inverse Dynamics on Optimization-based Dynamics
Proper Generalization of a Motion Cone
Key Takeaway
Whenever someone linearizes optimization-based dynamics, ask them if they've considered their domains for dual feasibility :)