Randomized Smoothing

for Trajectory and Policy Optimization

Terry

Two Approaches to Optimal Control in Robotics

Differential Dynamics and Optimization

Tabular MDP and Approximate DP

Motivation: what explains the empirical success of RL methods? How do we "translate" what they did in a language that we (I) understand better, and use it for better performance? Is it the stochasticity? Is it the zero-order nature of their algorithms?

\begin{aligned} \min_{x_t,u_t} & \quad \sum^{T-1}_{t=0} r(x_t,u_t) + r_T(x_T) \\ \text{s.t.} & \quad x_{t+1} = f(x_t, u_t) \end{aligned}
(S,A,R,T,\gamma)

Deterministic 

Rely on Analytical Gradients

Continuous State

Stochastic

Zero-order & Sampling

Discrete State

\dot{x}=f(x,u)

Robotics Problems

Nonlinear

Programming

Approximate Dynamic Programming

Robotics: Non-smooth, Non-convex Optimization

What are robotic problems? Why are they hard? 

1. The optimal control problems are non-convex (and not gradient-dominant) - nonlinear dynamics.

2. The optimal control problems are non-smooth (contact, combinatorial choices).

3. Sometimes, optimal control problems can have discontinuities.

Problems in robotics are usually continuous state, reasonably deterministic problems.

\dot{x}=f(x,u)

We should expect to solve optimal control problems under such dynamics and costs with a deterministic policy. (i.e. there is nothing stochastic about the problem). 

Deterministic, Non-convex, Non-smooth Problems.

Challenges in Differential Optimization: Nonconvexity

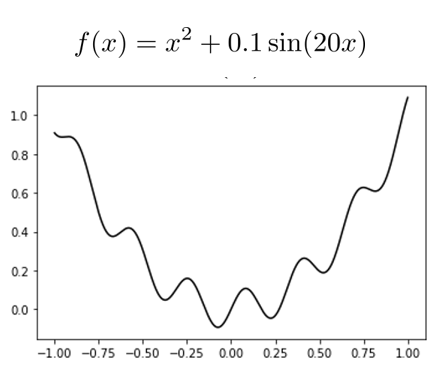
Non-convex (more precisely, not gradient dominant) functions can get you stuck in local minima

Often hinders good behavior in non-convex optimization:

Gradient is local (only looks at pointwise rate-of-change)

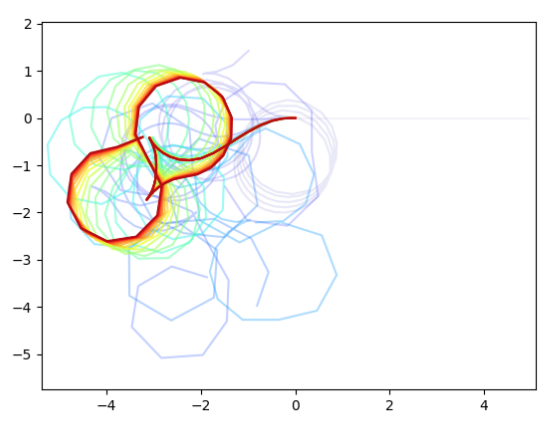
Trajopt for Car

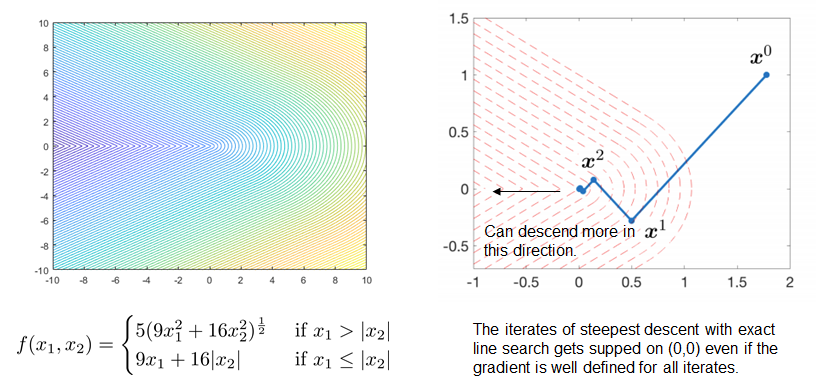
Challenges in Differential Optimization: Non-smoothness

Gradient descent can be arbitrarily bad (even fail to converge to stationary points) for non-smooth problems. 

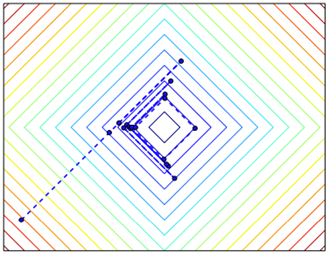
L1 minimization

Gradients in Robotics

The optimal control problems we solve in robotics are of non-convex, non-smooth nature.

But our tools behind typical optimization (SNOPT, etc.) are mostly gradient-based optimizers.

Natural that such solutions will be "fragile" (e.g. sensitive to initial guesses).

Robotics relies a lot on gradients....

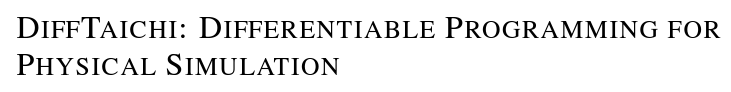
Randomized Smoothing: Couple Insights

Randomized Smoothing

\min_x f(x)

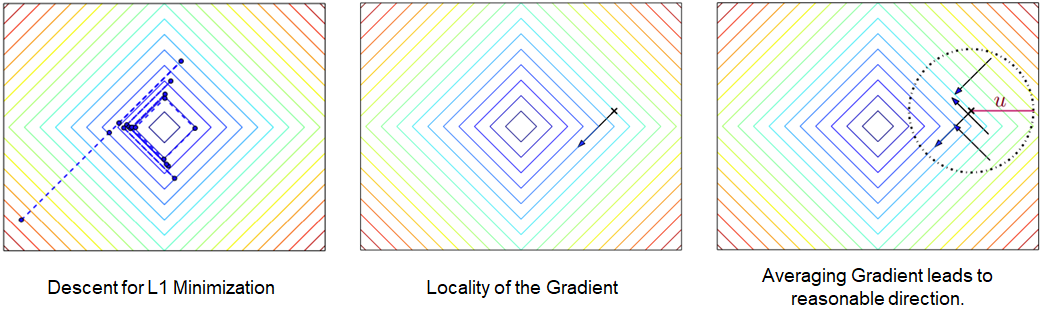
f is non-convex, potentially non-smooth. Not uncommon to have discontinuities. Hard to use gradients.

\min_x \mathbb{E}_{w\sim\mu} f(x+w)
\min_x \mathbb{E}_{w\sim\mu} f(x+w)

Introduce noise in the decision variables. How does this make the problem better?

Original Objective

Surrogate Objective

Randomized Smoothing as Convolution

\begin{aligned} \mathbb{E}_{w\sim\mu} f(x+w) & = \int f(x+w)\mu(w)dw \end{aligned}

Convolution between original objective and the distribution.

  • Smooths out high-frequency features of the cost to make the landscape nicer. 
  • Under choice of adequate kernels, convolution is guaranteed to be smooth.
  • Lowers the Lipschitz constant of the resulting objective.

Gradient computation

\begin{aligned} \nabla_x \mathbb{E}_{w\sim\mu} f(x+w) & = \mathbb{E}_{w\sim\mu} \nabla_x f(x+w) \\ & \approx \frac{1}{N}\sum^N_{i=1} \nabla_x f(x+w_i) \qquad w_i\sim\mu \end{aligned}
\nabla_x \mathbb{E}_{w\sim\mu} f(x+w)

Given information about                    , how do we compute the gradient of 

f, \nabla_x f

Best case: we are given some analytical closed-form expression for                                    , but highly unlikely.

\mathbb{E}_{w\sim\mu} f(x+w)

Standard trick: Exchange expectation and derivative, then use Monte-Carlo to approximate expected value. 

This is the "gradient sampling" algorithm - we can average a bunch of gradients and do descent with it, as opposed to the local gradient at the current iterate.

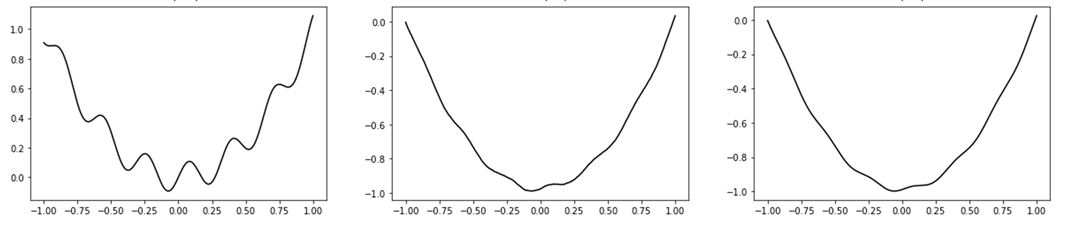
Failure Mode: Discontinuities 

\begin{aligned} \nabla_x \mathbb{E}_{w\sim\mu} f(x+w) & = \mathbb{E}_{w\sim\mu} \nabla_x f(x+w) \\ & \approx \frac{1}{N}\sum^N_{i=1} \nabla_x f(x+w_i) \qquad w_i\sim\mu \\ & \rightarrow 0 \end{aligned}

The algorithm has a particular failure case: functions with discontinuities. 

Example: Consider Heaviside function. 

f(x) = \begin{cases} 1 & \text{ if } x\geq 0 \\ 0 & \text{ if } x < 0 \end{cases}
\mathbb{E}_w f(x+w) = \text{erf}(x)
\nabla f(x) = \delta(x)

Staircase Effect in Non-smoothness

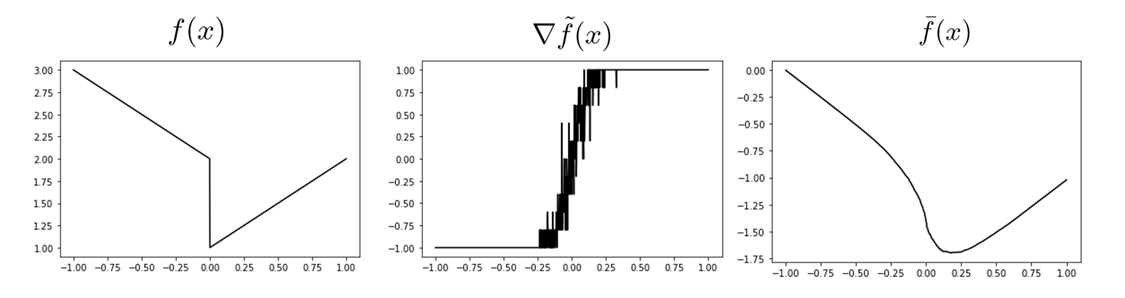
For non-smooth problems, can get a reasonable approximation.

But the quality of the approximation can be compromised in low-sample regimes.

(Staircase Effect)

Zero-order Variant

So how do we use randomized smoothing if the objective function is discontinuous?

One alternative is to take an expectation of finite differences instead: 

\begin{aligned} \mathbb{E}_{w\sim\mu}\bigg[\frac{f(x+w)-f(x)}{w}\bigg] \end{aligned}
\begin{aligned} \mathbb{E}_{w\sim\mu}\nabla f(x+w) \end{aligned}

1. Doesn't require f to be differentiable

2. More robust to numerics of discontinuities. 

3. In fact, why should we use the gradient instead of the zero-order version, since we're sampling anyways?

Randomized Smoothing of the Value Function

\begin{aligned} \min_\theta & \; V(x,\theta) = c_T(x_T) + \sum^{T-1}_{t=0} \gamma^t c(x_t, u_t) \\ \text{s.t.} & \; x = x_0 \\ & \; x_{t+1} = f(x_t, u_t) \\ & \; u_t = \pi(\theta, x_t) \end{aligned}

Consider solving the following problem for deterministic initial condition and deterministic dynamics.

This setting covers the following problems:

  • Open-loop policy optimization (i.e. trajectory optimization). Policy is simply parameterized as sequence of open-loop inputs.
  • Closed-loop policy optimization from fixed initial state. (Typical policy optimization deals with expected value of this over multiple initial conditions)

Why might this problem be hard to tackle with typical gradients?

  1. Non-convexity of the optimization landscape (value function w.r.t. policy parameters).
  2. Non-smoothness that arises in some typical problems inherent in RL problems.

Toy Problem: Throwing Ball against the Wall

\begin{aligned} \min_\theta & \; V(x,\pi_\theta) = -x_T^2\\ \text{s.t.} & \; x = x_0 \\ & \; x_{t+1} = f(x_t, u_t) \\ & \; u_0 = \theta, u_t=0 \end{aligned}

Back to high-school physics: suppose we throw a ball (Ballistic motion) and want to maximize the distance thrown using gradient descent.

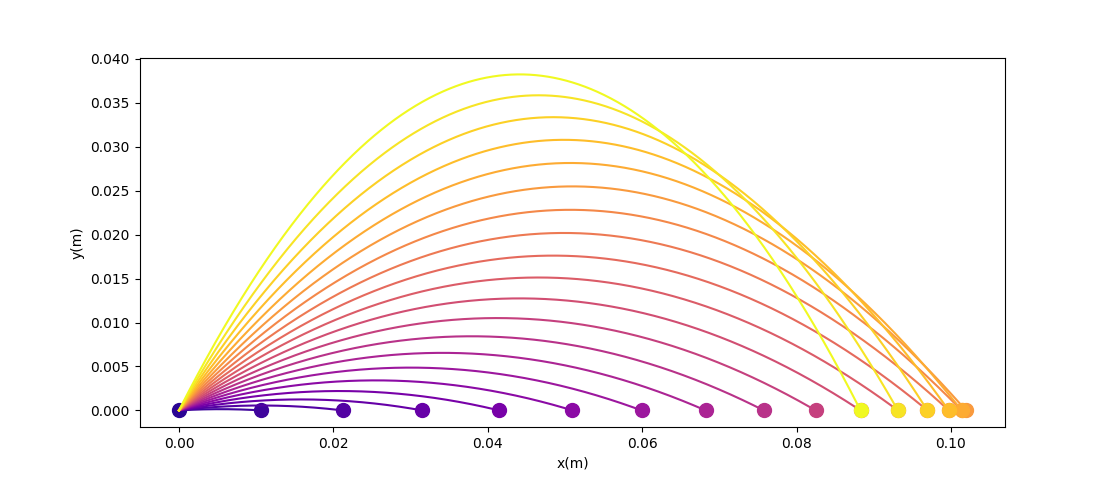
Quiz: what is the optimal angle for maximizing the distance thrown?

Toy Problem: Throwing Ball against the Wall

\begin{aligned} \min_\theta & \; V(x,\pi_\theta) = -x_T^2\\ \text{s.t.} & \; x = x_0 \\ & \; x_{t+1} = f(x_t, u_t) \\ & \; u_t = \theta \end{aligned}

Back to high-school physics: suppose we throw a ball (Ballistic motion) and want to maximize the distance thrown using gradient descent.

Quiz: what is the optimal angle for maximizing the distance thrown?

45 degrees!

If we plot the objective as a function of the angle, it is a nice gradient dominant function that will converge to the local minima.

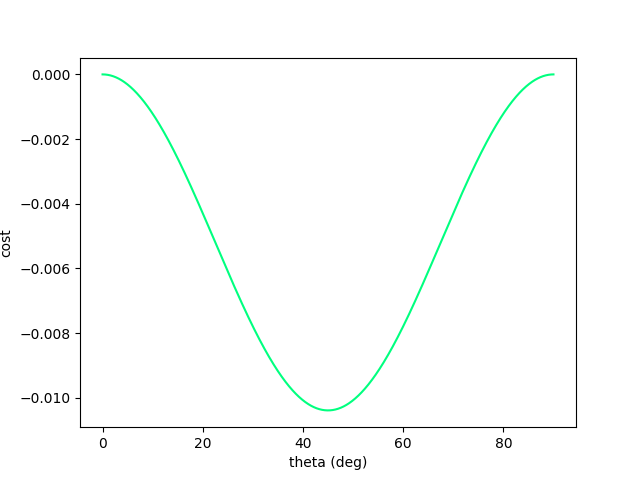
(Interestingly, this is non-convex. Typical example of one of Jack's PL inequality functions).

Toy Problem: Throwing Ball against the Wall

\begin{aligned} \min_\theta & \; V(x,\pi_\theta) = -x_T^2\\ \text{s.t.} & \; x = x_0 \\ & \; x_{t+1} = f(x_t, u_t) \\ & \; u_t = \theta \end{aligned}

Back to high-school physics: suppose we throw a ball (Ballistic motion) and want to maximize the distance thrown using gradient descent.

Now we no longer have such nice structure....gradient descent fails.

There is fundamentally no local information to improve once we've hit the wall!

Even though the physical gradients are very well defined, we can no longer numerically obtain the minimum of the function.

Now let's add a wall to make things more interesting. (Assume inelastic collision with the wall - once it hits, falls straight down)

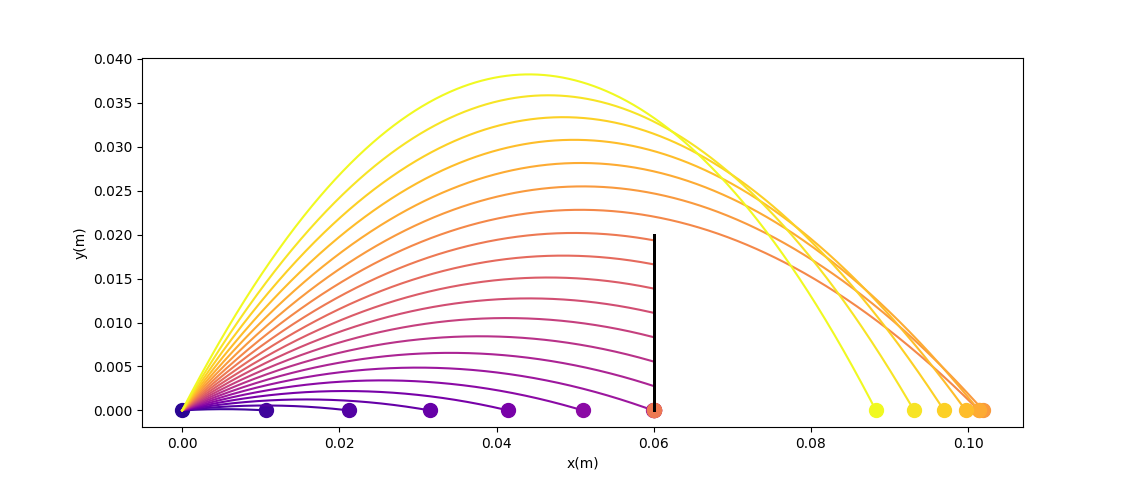
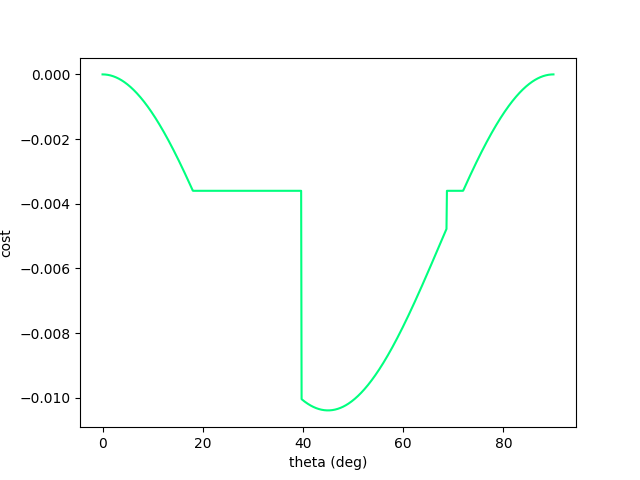
Randomized Smoothing to the Rescue.

\begin{aligned} \min_\theta & \; \mathbb{E}_{w\sim \mu} \big[V(x,\pi_\theta) = -x_T^2\big] \\ \text{s.t.} & \; x = x_0 \\ & \; x_{t+1} = f(x_t, u_t) \\ & \; u_t = \theta + w \quad w \sim \mu \end{aligned}

Back to high-school physics: suppose we throw a ball (Ballistic motion) and want to maximize the distance thrown using gradient descent.

Now we have recover gradient dominance! Now we know where to go when we've hit the wall.

Note: there might exist an inflection point. But zero probability of landing there during gradient descent iterations?

To resolve this, consider a stochastic objective by adding noise to the decision variable:

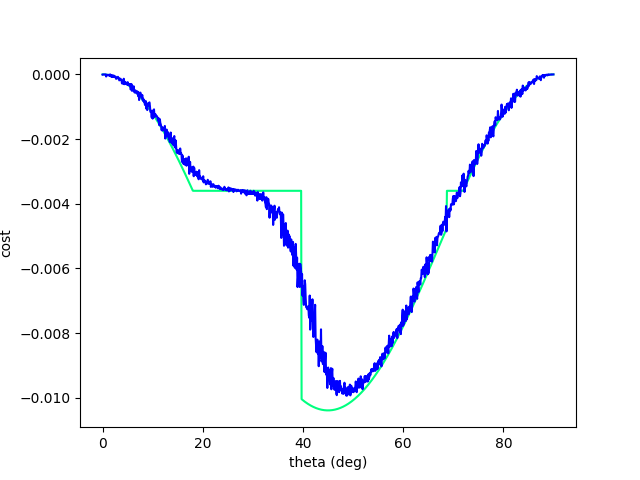
Similar Examples: Lessons from Differentiable Sim.

Excerpt from Difftaichi, one of the big diff. sims.

Rather surprising that we can tackle this problem with a randomized solution, without:

  • manual tuning of initial guesses
  • tree / graph search.

(Or rather, it was surprising to me at the beginning that gradients can't tackle this problem, the problem seems pretty easy and a search direction seems to exist.)

Some Connections

When are randomized policies better than deterministic policies?

The fact that you can obtain better performance with randomization in the presence of discontinuities is not new.

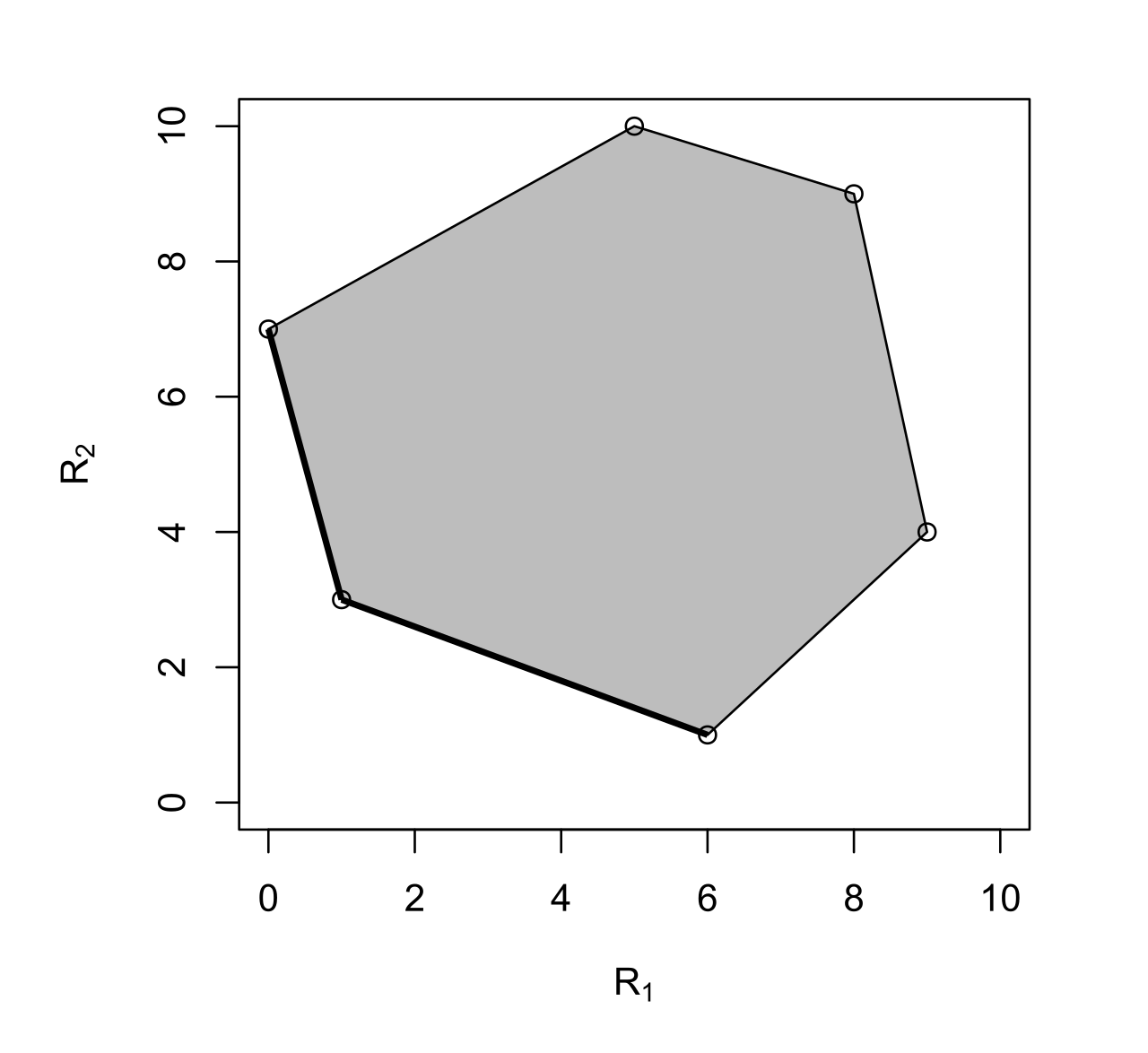
Binary Hypothesis Testing / Statistical Decision Theory (Neyman Pearson)

Deterministic Rules

Pareto Frontier

\begin{aligned} \min & \; R_1 \\ \text{s.t.} & \; R_2 \leq \alpha \end{aligned}

By randomizing, you can achieve better performance using the Neyman-Pearson criteria:

Danger of Gradient Strikes Again.

So we know that the stochastic objective is better for a more global search.

The problem is that we can no longer have a good way to utilize the gradient when the objective function is discontinuous.

Randomized Smoothing Policy Optimization

\begin{aligned} \min_\theta & \; \mathbb{E}_{x\sim\rho}\bigg[V(x,\pi_\theta) = c_T(x_T) + \sum^{T-1}_{t=0} \gamma^t c(x_t, u_t)\bigg] \\ \text{s.t.} & \; x = x_0 \\ & \; x_{t+1} = f(x_t, u_t) \\ & \; u_t = \pi(\theta, x_t) \end{aligned}
\begin{aligned} \min_\theta & \; \mathbb{E}_{x\sim\rho,w\sim\mu}\bigg[V(x,\pi_\theta) = c_T(x_T) + \sum^{T-1}_{t=0} \gamma^t c(x_t, u_t)\bigg] \\ \text{s.t.} & \; x = x_0 \\ & \; x_{t+1} = f(x_t, u_t) \\ & \; u_t = \pi(\theta + w, x_t) \quad w\sim \mu \end{aligned}

Note: In "Policy Optimization", we deal with optimization of closed-loop policy parameters.

Original Problem

Surrogate Problem

We think the surrogate problem has a nicer landscape compared to the original problem, w.r.t. two criteria:

  • "Gradient dominance" of the landscape. 
  • Flatness / discontinuity of the gradients.

 

which suggests an algorithm to use the surrogate problem to better solve the original problem.

 

Sorry hold on! 

Analytical Policy Gradient

\begin{aligned} \frac{\partial c}{\partial x}, \frac{\partial c}{\partial u}, \frac{\partial f}{\partial x},\frac{\partial f}{\partial u}, \frac{\partial \pi}{\partial \theta} \end{aligned}

Given the access to the following gradients:

One can use the chain rule to obtain the analytic gradients, that can be computed efficiently using autodiff on the rollout:

\begin{aligned} \nabla_\theta V(x,\pi_\theta) \end{aligned}

Conceivably, this can be used to update the parameters of the policy.

Policy Gradient Sampling Algorithm

Initialize some parameter estimate

While desired convergence:

Sample some initial states

\begin{aligned} \theta_0 \end{aligned}
\begin{aligned} x_i\sim\rho \end{aligned}

Compute the analytical gradient of the value function from each sampled state.

\begin{aligned} \nabla_\theta V(x_i,\pi_\theta) \end{aligned}

Average the sampled gradients to obtain the gradient of the expected performance:

\begin{aligned} \hat{\nabla}_\theta \mathbb{E}_{x\sim\rho} [V(x,\pi_\theta)] \approx \frac{1}{N}\sum^N_i \nabla_\theta V(x_i,\pi_\theta) \end{aligned}

Update the parameters using gradient descent / Gauss-Newton.

\begin{aligned} \theta_{k+1} = \theta_k - \alpha \hat{\nabla}_\theta \mathbb{E}_{x\sim\rho}[V(x,\pi_\theta)] \end{aligned}

Delta Strikes Again: Discontinuous Value Functions

Recall the following theorem: For discontinuous functions,  

\begin{aligned} w_i\sim\rho,\quad \frac{1}{N}\sum^N_{i=1}\nabla_\theta f(\theta, w_i) \xrightarrow[]{a.s.} \nabla_\theta \mathbb{E}_{w\sim\rho} [f(\theta,w)] \end{aligned}

Recall the following theorem: For discontinuous functions,  

We've previously looked at this in the context of contact dynamics, but the policy search suffers from similar problems.

\begin{aligned} \hat{\nabla}_\theta \mathbb{E}_{x\sim\rho} [V(x,\pi_\theta)] \neq \frac{1}{N}\sum^N_i \nabla_\theta V(x_i,\pi_\theta) \text{ if } V(x,\pi_\theta) \text{ is discontinuous} \end{aligned}

But unlike contact dynamics (non-smooth but mostly continuous), the value function may truly suffer from many discontinuities.

Meaningful Question to ask: For which class of specifications / problems do we have discontinuous value functions?

  • Could it appear for smooth systems in the presence of constraints? 
    • Viscosity solutions to the HJB equation: usually nonsmooth, but not quite discontinuous 
    • torque-limited pendulum (courtesy of Jack)
  • Non-smoothness / Bifurcation in Dynamics
  • Discontinuities in Cost  

Zero-Order Policy Update

\begin{aligned} \min_\theta & \; \mathbb{E}_{x\sim\rho,w\sim\mu}\bigg[V(x,\pi_\theta) = c_T(x_T) + \sum^{T-1}_{t=0} \gamma^t c(x_t, u_t)\bigg] \\ \text{s.t.} & \; x = x_0 \\ & \; x_{t+1} = f(x_t, u_t) \\ & \; u_t = \pi(\theta + w, x_t) \quad w\sim \mu \end{aligned}

How do we solve the surrogate problem? Start with zero-order optimization.

Surrogate Problem

1. Sample the perturbations of the policy parameters.

 

 

 

2. Compute a direction of improvement w.r.t. policy parameters.

 

 

 

3. Update policy parameters with the computed direction.

 

 

4. Decrease the variance on injected noise as iterations converge.

\begin{aligned} \mathbb{E}_{x\sim\rho,w\sim\mu}[V(x,\pi(\theta+w))] \approx \frac{1}{N\cdot M}\sum_{i=1}^N\sum_{j=1}^M V(x_j, \pi(\theta+w_i)) \end{aligned}
\begin{aligned} \hat{\nabla}^0_\theta \mathbb{E}_{x\sim\rho,w\sim\mu}[V(x,\pi(\theta+w)]\approx \frac{1}{N}\sum_{i=1}^N \bigg(\frac{\frac{1}{M}\sum_{j=1}^M \big[V(x_j, \pi(\theta+w_i))-V(x_j,\pi(\theta-w_i))\big]}{2 w_i}\bigg) \end{aligned}

Zero-Order Gradient Estimation (SPSA)

\begin{aligned} \theta_{k+1} = \theta_k - \alpha \nabla^0_\theta \mathbb{E}_{x\sim\rho,w\sim\mu}[V(x,\pi(\theta_k+w)] \end{aligned}

Randomized Smoothing Trajectory Optimization

Note: In "Trajectory Optimization", we deal with optimization of open-loop input sequences starting from a single initial point.

Original Problem (Single-shooting formulation)

Surrogate Problem

\begin{aligned} \min_{u_t} & \; V(x,\pi_\theta) = c_T(x_T) + \sum^{T-1}_{t=0} \gamma^t c(x_t, u_t) \\ \text{s.t.} & \; x = x_0 \\ & \; x_{t+1} = f(x_t, u_t) \\ \end{aligned}
\begin{aligned} \min_{u_t} & \; \mathbb{E}_{w_t\sim\mu_t,\forall t}\bigg[V(x,\pi_\theta) = c_T(x_T) + \sum^{T-1}_{t=0} \gamma^t c(x_t, u_t)\bigg] \\ \text{s.t.} & \; x = x_0 \\ & \; x_{t+1} = f(x_t, u_t+w_t) \\ \end{aligned}
\begin{aligned} \min_{u_t} & \; V(x,\pi_\theta) = c_T(x_T) + \sum^{T-1}_{t=0} \gamma^t c(x_t, u_t) \\ \text{s.t.} & \; x = x_0 \\ & \; x_{t+1} = \mathbb{E}_{w_t\sim\mu_t}\bigg[f(x_t, u_t+w_t)\bigg] \\ \end{aligned}

Note: Comparison with Previous Work

expectation over entire trajectory of noises

expectation over noise in a single timestep.

Question: how should we inject noise?

  • Introducing noise of same variance at every timestep leads to extremely high variance estimates 
  • Least variance is when we take a deterministic policy up until the last step and sample the last action. However, such a solution does not smooth out the objective much. 
  • Adding noise in the beginning of the trajectory leads to large variance. However, it is most effective in exploring different possibilities. 
  • Fundamental tension between variance and exploration when optimizing for sequential decisions in open loop. 

Variance Reduction vs. Exploration

Injecting noise right at the end of the trajectory will lead to a small variance among the distribution of value functions.

However, the capability to explore different solutions is extremely limited to a single timestep.

Injecting noise right at the front of the trajectory will lead to high variance among the distribution of value functions.

However, the method now has a lot of capability to explore. (Think of the ball throwing example)

What is the optimal way to trade off exploration vs. variance of the expected value function?

Perhaps we can reason about this in the space of increasing the width of the distribution for the latter part of the trajecotires.

\sigma(\small w_t) \propto \sqrt{t}

Example:

Randomized Smoothing Trajectory Optimization

We would like to use this for a more global exploration of contact modes.

Consider the following toy problem of pushing the box.

Goal configuration

Initial configuration

What we know about the problem:

  1. Without any smoothing whatsoever, the gradient is zero. Unable to find good directions of improvement.

  2. If we just smooth the dynamics and reason about the "bundled dynamics", cannot

  3.  

Randomized Smoothing of Contact Dynamics

\begin{aligned} \min_{u_t} & \; V(x,\pi_\theta) = c_T(x_T) + \sum^{T-1}_{t=0} \gamma^t c(x_t, u_t) \\ \text{s.t.} & \; x = x_0 \\ & \; x_{t+1} = \mathbb{E}_{w_t\sim\mu_t}\bigg[f(x_t, u_t+w_t)\bigg] \\ \end{aligned}

Smoothing of the Objective

\begin{aligned} \min_{u_t} & \; \mathbb{E}_{w_t\sim\mu_t,\forall t}\bigg[V(x,\pi_\theta) = c_T(x_T) + \sum^{T-1}_{t=0} \gamma^t c(x_t, u_t)\bigg] \\ \text{s.t.} & \; x = x_0 \\ & \; x_{t+1} = f(x_t, u_t+w_t) \\ \end{aligned}

Smoothing of the Dynamics

Questions, questions, and more questions.

1. What's the real tradeoff between analytical gradients (computed through symbolic / automatic diff), vs. numerical gradient? If there are considerable benefits to using analytical gradients (e.g. in higher dimensions), is there a way to modify the method for objectives with discontinuities?

2. What are useful questions for analysis? (Where do I go beyond the fact that this will "intuitively" help?) What are theoretical characterizations of performance (variance of the Monte-Carlo approximation? convergence rate?)  under which cases?

3.  Should we sample from the parameters, or append noise to the output?