Quasistatic Deformable Simulation
Current formulation of simulation
minΩs.t.∫Ωρd(x;Ω0)2dv+∫∂Ω1dsψ(x)≥0∀x∈Ω∫Ωρdv=∫Ω0dv
\begin{aligned}
\text{min}_{\Omega}\quad & \int_{\Omega} \rho d(x;\Omega_0)^2 dv + \int_{\partial\Omega} 1 ds \\
\text{s.t.} \quad & \psi(x) \geq 0 \quad \forall x\in\Omega\\
& \int_{\Omega} \rho dv = \int_{\Omega_0} dv
\end{aligned}
dL(Ω;V)=∫∂Ω(d(x;ω0)+H(x)+μ−λ(x)ψ(x))V(0)⋅nds
\begin{aligned}
d \mathcal{L}(\Omega;V) & = \int_{\partial\Omega} \left( d(x;\omega_0) + H(x) + \mu - \lambda(x)\psi(x) \right) V(0) \cdot n ds
\end{aligned}
Formulation
Shape gradients & Optimality conditions
μ
\begin{aligned}
\mu
\end{aligned}
λ(x)∀x∈Ω
\begin{aligned}
\lambda(x) \quad \forall x \in \Omega
\end{aligned}
dL(Ω;V)=∫∂Ω(d(x;ω0)+H(x)+μ−λ(x)ψ(x))V(0)⋅nds
\begin{aligned}
d \mathcal{L}(\Omega;V) & = \int_{\partial\Omega} \left( d(x;\omega_0) + H(x) + \mu - \lambda(x)\psi(x) \right) V(0) \cdot n ds
\end{aligned}
λ(x)ψ(x)=0
\begin{aligned}
\lambda(x)\psi(x) = 0
\end{aligned}
λ(x)≥0∀x∈Ω
\begin{aligned}
\lambda(x) \geq 0 \quad \forall x \in\Omega
\end{aligned}
ψ(x)≥0∀x∈Ω
\begin{aligned}
\psi(x) \geq 0 \quad \forall x \in\Omega
\end{aligned}
∫Ω1dv=∫Ω01dv
\begin{aligned}
\int_\Omega 1 dv = \int_{\Omega_0} 1 dv
\end{aligned}
Duals
Implementation
we now have a "ShapeMathematicalProgram" which acts like Drake's MP
Program for mean curvature flow
2D Results
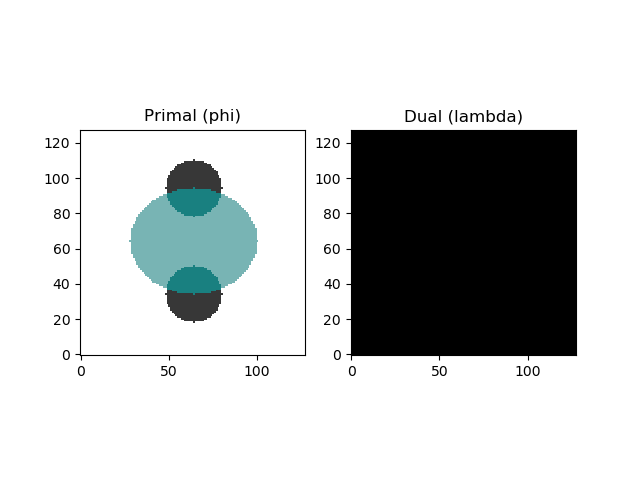
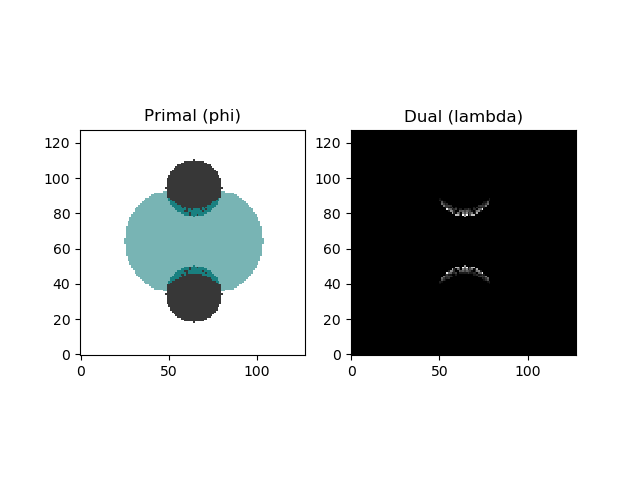
Initial iteration
Final iteration
2D Results
2D Results
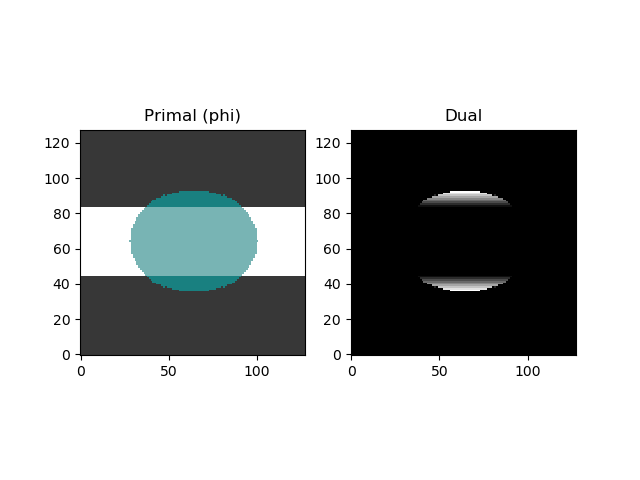
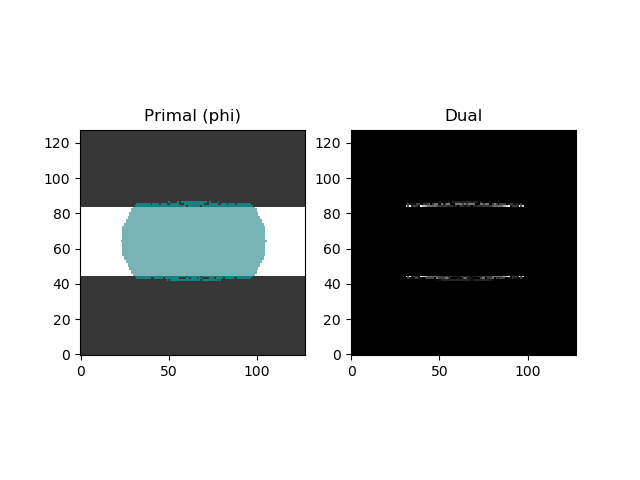
Initial iteration
Final iteration
2D Results
Comparison with PlasticineLab
Real Video
PlasticineLab
Bug / Feature: Slicing
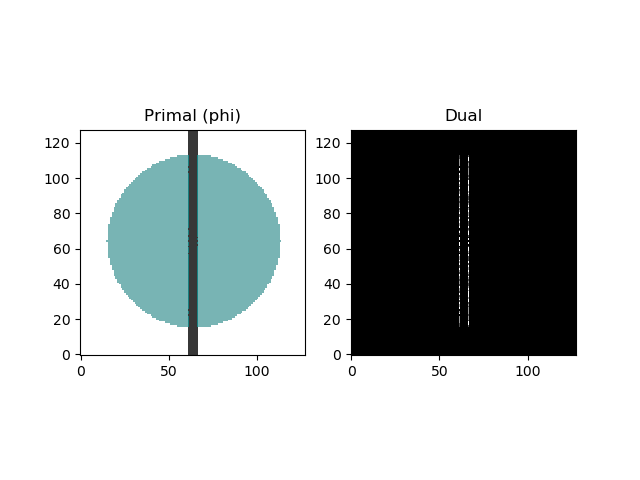
3D Simulation
Next Steps
Simulation side:
Planning side:
Hardware & Experiments:
- More scenarios to try, figure out limitations of this simulation method
- More simulators to set up and compare against - Nvidia PhysX / FleX
-
- Can we do better than MCTS....?
- Can we get a pottery table?
Quasistatic Deformable Simulation