La régression linéaire

Thierry FEUILLET

Univ. Caen

Quelques bases (ou rappels) de statistiques

  • La statistique est la science de la variation des données
  • Pas de variation, pas de statistique
  • Elle dispose d'un vocabulaire, dont les termes essentiels sont :
    • Individus statistiques
    • Variables
    • Echantillon/population
    • Variance/covariance

Individus statistiques

  • Ils correspondent aux lignes d'un tableau
  • C'est le niveau élémentaire de mesure d'un phénomène

Variables

  • Séries de caractères ou modalités pris par les individus
  • Il existe plusieurs types de variables, qu'il faut savoir identifier
  • Exemples : taille, couleur des cheveux, notes aux partiels, budget des clubs de foot…

Variables : deux grands types

  • Variables quantitatives
    • Les caractéristiques des individus sont des valeurs
  • Variables qualitatives
    • Les caractéristiques des individus sont des modalités

Variables : deux grands types

  • Variables qualitatives ordinales
    • Ordonnées selon une échelle de valeurs (niveau d’étude, score d’appréciation, etc.)
  • Variables qualitatives nominales
    • les classes ne peuvent pas être hiérarchisées (sexe, nationalité, type de roches, etc.)

Variables : deux grands types

  • Variables binaires
    • Variables dichotomiques (absence/présence)
    • Variables booléennes (vrai/faux)
    • Variables de Bernouilli (0/1)

Variables : deux grands types

  • Variables quantitatives discrètes
    • Moins de valeurs que d’individus (nombre d’enfants, notes à un devoir, etc.)
  • Variables quantitatives continues
    • Peuvent prendre un nombre infini de valeurs au sein d’un intervalle (tous les taux, altitude, taille, etc.)

Variables : deux grands types

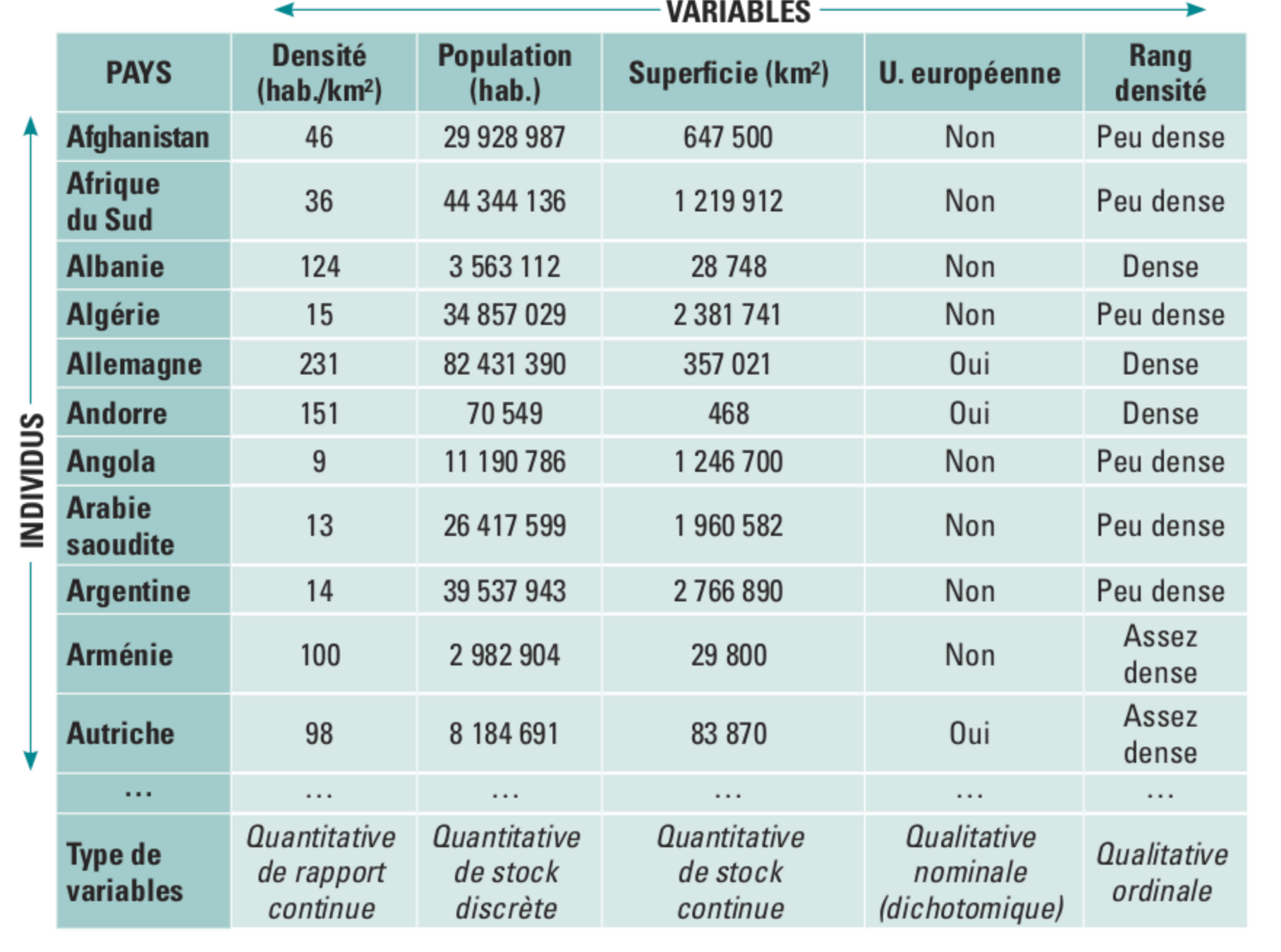
Pourquoi distinguer les variables ?

  • Variables quantitatives discrètes
    • Moins de valeurs que d’individus (nombre d’enfants, notes à un devoir, etc.)
  • Variables quantitatives continues
    • Peuvent prendre un nombre infini de valeurs au sein d’un intervalle (tous les taux, altitude, taille, etc.)

Echantillon

  • Echantillon = Groupe d’individus sélectionnés dans une population (ou un ensemble)
  • Par exemple : votre classe (par rapport à tous les étudiants de France), les communes de Seine-Saint-Denis, etc.

Population

  • Population = l’ensemble des données étudiées
  • Par exemple : les pays du monde, les départements français, tous les étudiants, toutes les communes, etc.

Points très importants

  • Les résultats statistiques issus d’un échantillon ne valent pas forcément pour la population (inférence)

  • Dépend en grande partie de la taille et de la représentativité de l’échantillon

Mesurer les variations : les paramètres de dispersion

  • La variance est le paramètre le plus utilisé en stat

  • C'est une mesure de la variation des valeurs d'une variable autour de sa moyenne

\sigma² = \frac{1}{N} \sum_{i = 1}^{n} (x_i-\overline{x})^2

Mesurer les variations : les paramètres de dispersion

  • L'écart-type est la racine carrée de la variance

  • Le coefficient de variation est l'écart-type divisée par la moyenne (annule les effets des unités de mesure variables)

Mesurer les covariations

  • La covariance mesure l'association entre deux variables quantitatives

  • Elle peut être négative, nulle ou positive

cov_{x,y}=\frac{\sum_{i=1}^{N}(x_{i}-\bar{x})(y_{i}-\bar{y})}{N-1}

Mesurer les covariations

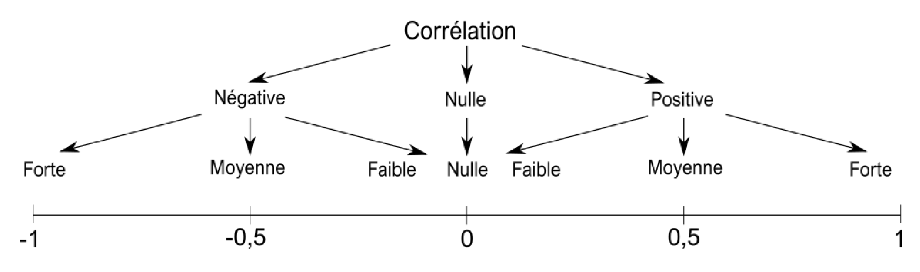
  • Le coefficient de corrélation linéaire est le rapport entre la covariance et le produit des écart-types de x et y

r=\frac{cov_{xy}}{\sigma_x\sigma_y}

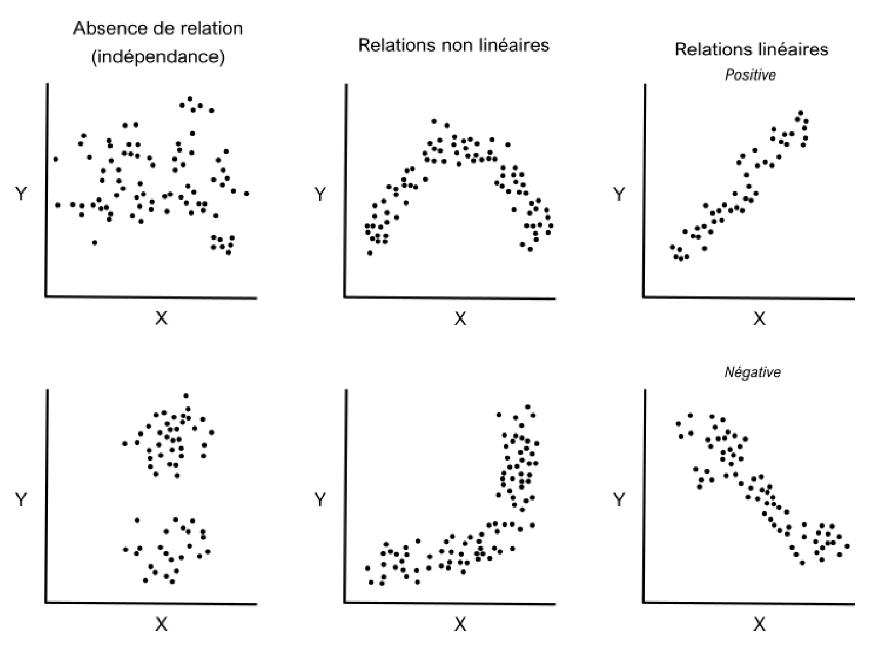
Mesurer les covariations

La régression linéaire

La RL est la méthode qui permet d'estimer l'équation de cette droite

  • Estime des relations
  • Prédit des valeurs

RL = principale méthode de modélisation statistique

  • La modélisation statistique se définit en fonction de ses finalités
    • Approche descriptive
    • Approche explicative
    • Approche prédictive

Approche descriptive

  • A pour but d’explorer les liens entre une variable réponse et une série de variables explicatives potentielles => statistiques multivariées privilégiées

Approche explicative (ou déductive)

  • Utilise la connaissance que l’on a d’un système pour tester le pouvoir explicatif d’un petit nombre de variables sur une variable réponse => modèles statistiques inférentiels (ex. régression)

Approche prédictive

  • Cherche à prédire au mieux les valeurs de la variable réponse, sans forcément décrire ou comprendre les données => algorithmes boite noire type apprentissage machine

La modélisation statistique

  • Les statistiques incorporent l'incertitude (via les probabilités) et sont donc particulièrement adaptées aux sciences humaines et sociales (contrairement aux modèles physiques déterministes)

La modélisation statistique

  • Les statistiques vont permettre d'estimer des paramètres décrivant la structure des phénomènes étudiés
  • Par exemple : l'analyse de la relation entre 2 variables X et Y consiste à estimer le "a" de l'équation y = ax + b
  • "a" représente le paramètre structurel de la relation (très proche de r) et est un fait virtuel (car résulte d'une stratégie du modélisateur et non déterminé par l'empirie)

Formulation du modèle

  • Importance du terme stochastique

 

 

  • Cette relation fonctionnelle n'est pas un modèle statistique, car il n'y a pas de terme d'erreur

 

  • Yi peut dépendre d'autres variables, et d'erreurs de mesure, etc.
Y_i = f(X_i)

Formulation du modèle

  • On notera alors :

 

 

  • où єi représente le terme d'erreur stochastique. On est ici bien en présence d'un modèle statistique
  • Ce terme représente la différence entre un modèle déterministe et un modèle stochastique (ou probabiliste)
Y_i = f(X_i) + \epsilon_i

La régression linéaire simple

  • Un des modèles statistiques les plus courants
  • Consiste à modéliser la covariation entre une variable dépendante Y (ou à expliquer) et une variable indépendante X (ou explicative)

Les deux usages de la régression

  • Prédire ==> les valeurs de Y dans des lieux non mesurés ou dans le futur
  • Comprendre ==> Explorer la présence et l'intensité d'associations statistiques entre variables

La régression linéaire : intérêt pratique et cadre théorique

  • La régression s'applique à des variables dont la relation semble linéaire d'après le nuage de points et la valeur du coefficient de corrélation linéaire
  • Y est une variable à expliquer quantitative continue
  • X est une variable explicative quali ou quanti

La régression linéaire : intérêt pratique et cadre théorique

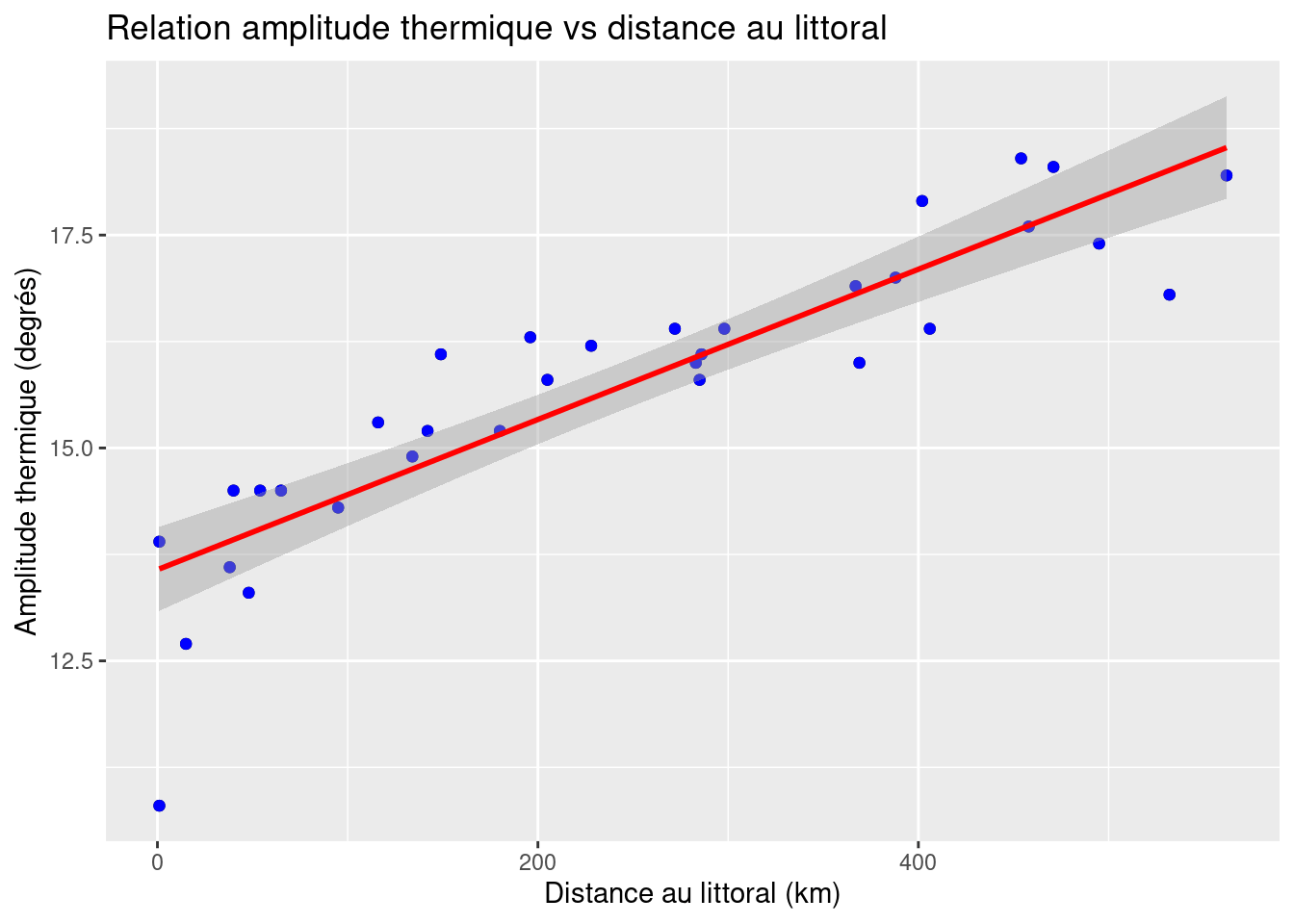
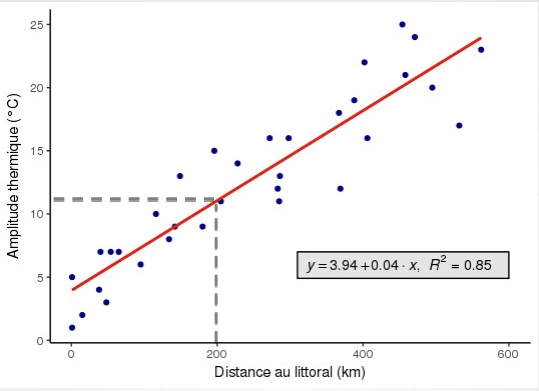
  • On voit ici que la fonction qui lie X et Y semble linéaire : quand la distance augmente, l'AT augmente, dans les mêmes proportions partout

La régression linéaire : intérêt pratique et cadre théorique

  • La régression linéaire est la méthode qui va permettre d'estimer l'équation de la droite qui ajustera au mieux ce nuage de points

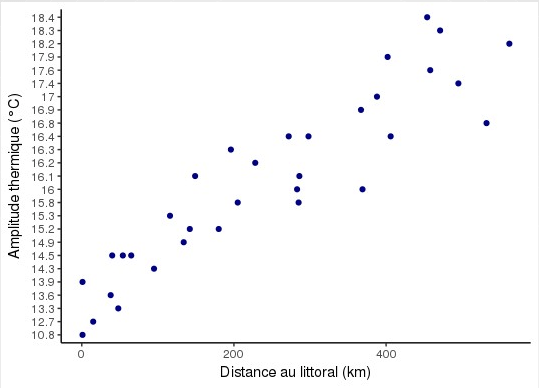
La régression linéaire : intérêt pratique et cadre théorique

  • Quel est l'intérêt de connaitre l'équation de cette droite ?

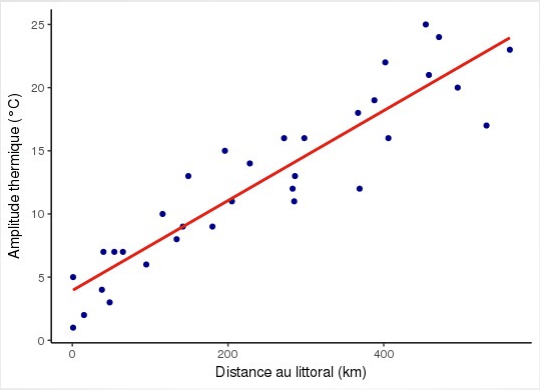
La régression linéaire : intérêt pratique et cadre théorique

  • Cela permet d'estimer la valeur de Y pour toutes valeurs de X

La régression linéaire : intérêt pratique et cadre théorique

  • D'après cette équation : une ville située à 200 km de l'océan aurait une amplitude thermique de 3,94 + 0,04 * 200 = 11,94

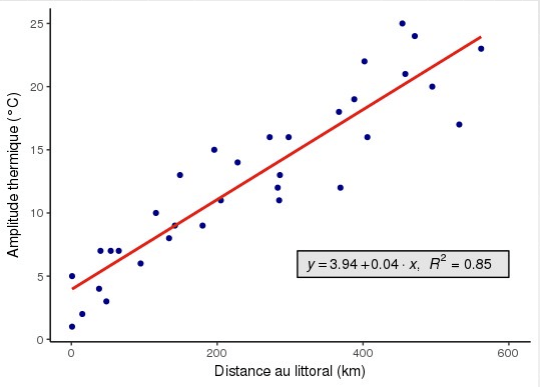
La régression linéaire : intérêt pratique et cadre théorique

  • Une augmentation de 10 km est associée à une augmentation de 0,4°C

La régression linéaire : intérêt pratique et cadre théorique

  • Le coefficient a (ici 0,04) correspond à la pente de la droite (ou coefficient directeur) : son signe détermine le sens de la relation
  • b (constante) = Y quand X = 0

La régression linéaire : intérêt pratique et cadre théorique

  • 0,04 correspond au rapport de la variation de Y sur la variation de X :
  • a = ΔY / ΔX
  • démonstration : (11,94-3,94)/200 = 8/200 = 0,04

Cadre théorique : la causalité

  • Le modèle théorique linéaire s'exprime ainsi :

 

 

 

 

  • où yi est la variable dépendante, xi la variable indépendante, β0 la constante et β1 la pente (ou coefficient de régression)
y_i = \beta_0 + \beta_{1}X_1 + \epsilon_i

Cadre théorique : la causalité

  • Selon cette équation, la relation est présumée causale, X expliquant Y
  • Or, la causalité ne relève que des hypothèses théoriques posées par le modélisateur
  • Des coefficients même significatifs peuvent cacher d'autres types de relations

Les mécanismes de la causalité

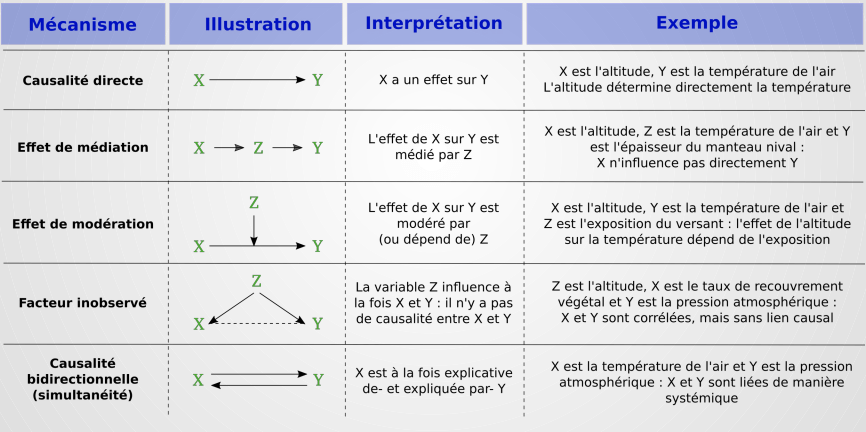
Les mécanismes de la causalité

  • La régression linéaire ne permet en aucun cas de prouver une quelconque causalité
  • ==> prudence dans l'interprétation des résultats !!

Le modèle empirique et l'estimation des paramètres

  • Le modèle théorique ne vaut que pour la population
  • On ne pourra donc jamais connaitre la valeur réelle de β0 et de β1
  • On ne pourra estimer que des estimateurs de ces paramètres, notés respectivement b0 et b1

Le modèle empirique et l'estimation des paramètres

  • L'équation du modèle empirique s'écrit donc :

 

 

  • Les résidus e sont des estimateurs des erreurs (epsilon)
y_i = b_0 + b_{1}x_1 + e_i

La droite des moindres carrés

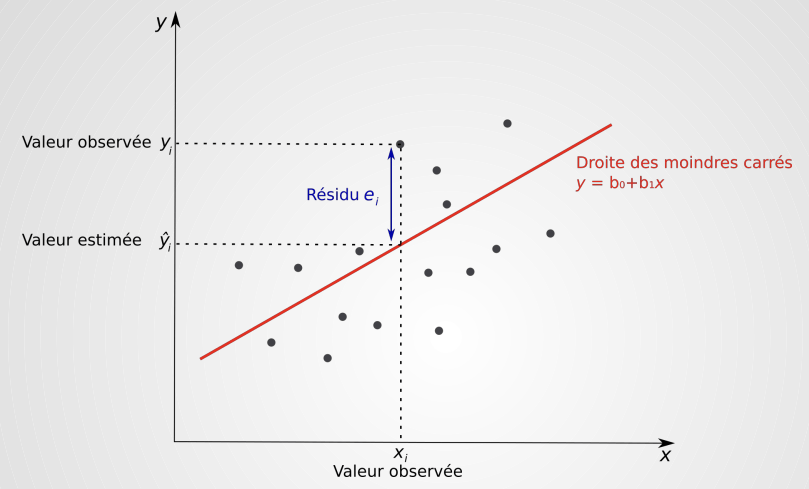
  • Les résidus représentent la différence entre les valeurs observées et les valeurs estimées de Y : :

 

e_i = y_i - \hat{y}_i

La droite des moindres carrés

  • La droite des moindres carrés est celle qui va minimiser la somme des carrés des résidus

Estimation de b1

\widehat{b_1} = \dfrac{cov(X,Y)}{var(X)}

Estimation de b0

\widehat{b_0} = \overline{Y} - \widehat{b_1}\cdot\overline{X}

Mesurer la qualité du modèle : le R^2

R^2 = 1-\frac{\sum_{n=1}^{n}(Y_i-\widehat{Y_i})^2}{\sum_{n=1}^{n}(Y_i-\overline{Y_i})^2}
  • Part expliquée de variance de Y. Varie entre 0 et 1

Inférence

  • La qualité globale du modèle (R²) est intéressante mais insuffisante
  • On veut aussi savoir si la relation entre X et Y est significative
  • Pour le savoir, on fait appel aux statistiques inférentielles (extrapolation de l'échantillon à la population)

Inférence

  • Rappelez-vous que b1 est un estimateur de β1 (l'effet vrai)
  • Il faut considérer b1 comme une variable aléatoire (imaginez qu'on ait 1000 échantillons)
  • Cette variable aléatoire suit à peu une loi normale (théorème central limite)

Inférence

  • On considère que cette variable a pour moyenne β1 et pour variance une valeur qui dépend de la variance des résidus et de la variance de X

  • Plus cette variance est faible, plus l'estimation est précise et fiable

Inférence

  • Il y a donc 3 manières de minimiser l'erreur type :
    - Augmenter la variance de X
    - Diminuer les résidus
    - Augmenter la taille de l'échantillon

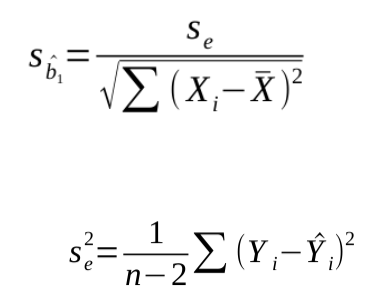
La t-value et la p-value

  • On cherche à savoir si l'effet réel de X sur Y (i.e. β1) est significativement différent de 0
     

  • Cette hypothèse se note :

    H0 : β1 = 0

La t-value et la p-value

  • Rappel : on ne dispose que d'un estimateur de β1 (b1)

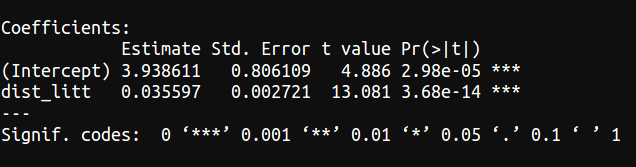
  • Dans notre exemple, b1 = 0,04

     

    Doit-on en conclure que comme 0,04 ≠ 0, il y a bien un effet de X sur Y ?

La t-value et la p-value

  • Mais imaginez que la vraie valeur soit 0, et que la valeur de 0,04 ne soit due qu'à une erreur d'échantillonnage ?

La t-value et la p-value

  • On va donc s'intéresser à la différence entre b1 et 0, différence que l'on rapporte à l'incertitude de b1
     
  • La quantité que l'on va tester est donc la suivante :

t = (b1－ 0)/s(b1)
soit
t = b1/s(b1)


C'est la t-value !

La t-value et la p-value

  • L'idée est que plus cette quantité est proche de 0, plus il y a de chances que l'effet de X sur Y soit nul
     

  • On connait la distribution théorique de t (théorème central limite), on peut donc estimer la probabiltié critique d'accepter H0 !

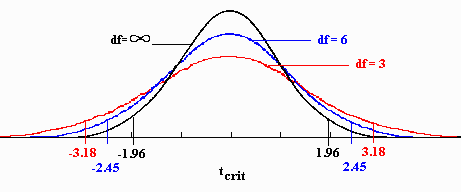
La loi de Student

  • si t > |1,96| => on a 95% de chances de rejeter H0 sans se tromper (quand n > 200)

Récapitulatif du test des coefficients de régression

  1. On pose l'hypothèse H0 : β1 = 0

  2. On rapporte b1-0 à son erreur type => c'est la t-value. Ce rapport (t) suit une loi de Student à n-2 DDL

  3. On choisit un seuil alpha (souvent 0,05)

  4. On rejète H0 si |t| > tα

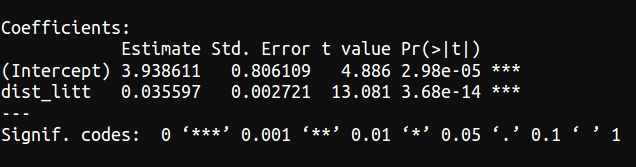
Dans notre exemple

  • On estime avec 99% de chances de ne pas se tromper que la distance au littoral a bien un effet sur l'amplitude thermique

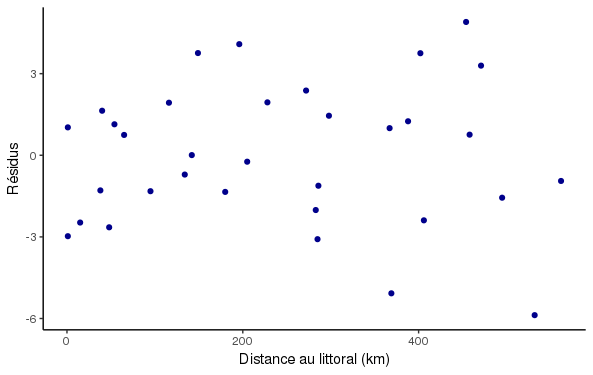
L'analyse des résidus

  • Plusieurs hypothèses doivent théoriquement être respectées pour s’assurer des estimations BLUE (best linear unbiased estimators)

  • La plupart de ces hypothèses concernent les résidus

Les hypothèses stochastiques

  • Les résidus ont une distribution normale et une moyenne nulle

  • Ils ont une variance constante (homoscédasticité), i.e. sont indépendants de X

  • Ils sont indépendants entre eux

Les hypothèses stochastiques

  • Par exemple, si les résidus sont hétéroscédastiques, cela indique un pb de spécification du modèle (variable manquante)

  • S’ils sont autocorrélés (notamment dans l’espace), la variance de b est sous-estimée (car information redondante, donc n plus petit qu’en réalité)

Hétéroscédasticité

Les autres conditions essentielles

  • En régression linéaire, Y doit être distribuée selon une loi normale

  • Les relations entre Y et X sont linéaires

La régression multiple

  • Souvent, une variable explicative ne suffit pas pour expliquer le phénomène étudié

  • Dans notre exemple, nous n'expliquions "que" 80% de la variance de Y environ

  • Il est possible d'intégrer d'autres variables explicatives dans le modèle

  • On parle alors de régression multiple

La régression multiple

  • La régression multiple s'écrit :

 

 

 

où k est le nombre de variables explicatives

y_i = \beta_0 + \beta_1x_1 + \beta_2x_2 + ... + \beta_kx_k + e_i

La régression multiple

  • Les estimations, tests et analyses de résidus se généralisent facilement à la RM

  • Par contre, l'interprétation des coefficients se fait toutes choses égales par ailleurs, c'est-à-dire en contrôlant l'effet des autres variables

Sélection des variables explicatives

  • Une hypothèse de la RM stipule que les VE ne doivent pas être colinéaires

    Cela biaise les estimations

Matrice de corrélation

  • On peut construire cette matrice et éliminer les coefficients > 0,7 en valeur absolue

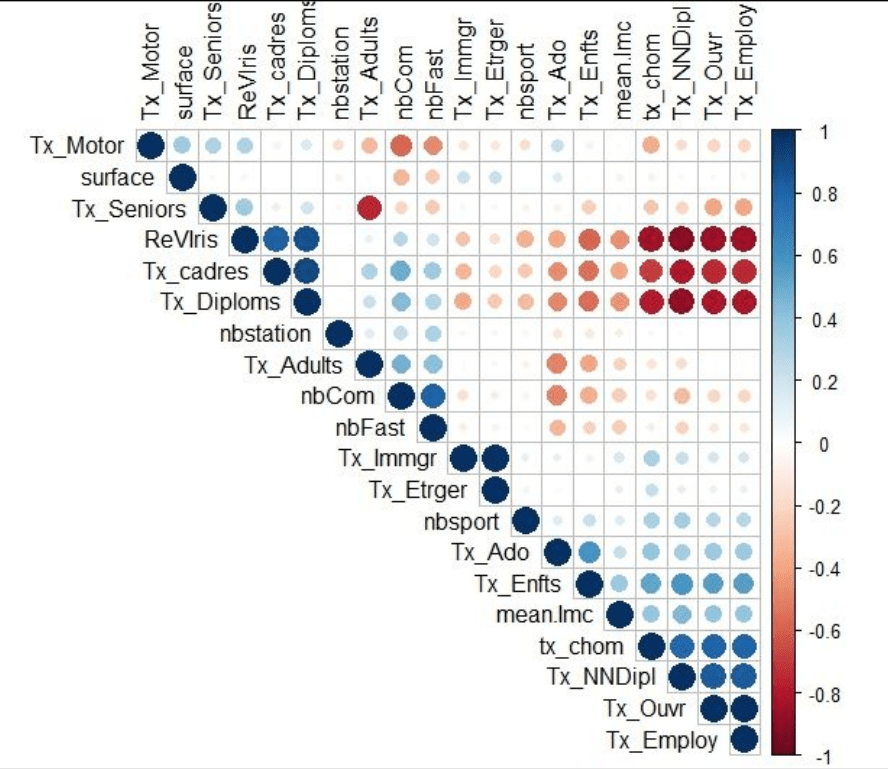
La VIF
(variance inflation factor)

  • Une autre méthode plus poussée consiste à calculer la VIF

 

 

 

 

 

  • On régresse chaque VE par toutes les autres
  • Si VIF > 3 ==> supprimer la VE
VIF(X_j) = \frac{1}{1 - R^2_j}

La sélection automatique de variables

  • Sélection pas à pas ascendante

  • Sélection pas à pas descendante

 

  • Pas à pas ascendante : on ajoute les variables une à une et on ne retient que celles qui maximisent le R² ou qui sont significatives
  • Pas à pas descendante : on part du modèle complet et on retire les variables non significatives une à une

Application - récapitulatif procédure

  1. Poser les hypothèses théoriques

  2. Formulez le modèle théorique
  3. Vérifiez la multicolinéarité des X
  4. Vérifiez la normalité de Y et la linéarité des relations deux à deux
  5. Formulez le modèle empirique
  6. Estimez le modèle empirique
  7. Testez les coefficients
  8. Interprétez les résultats et concluez