Existence of optimal maps
for the Gromov-Wasserstein problem
Théo Dumont
D., Lacombe, Vialard. On the Existence of Monge maps for the Gromov-Wasserstein problem, FoCM 2024


slides available at https://slides.com/theodumont/monge-gw

1. Short intro to optimal transport


Gaspard Monge
Leonid Kantorovitch

[Monge, 1781], [Kantorovitch, 1942]
- a measure over a set \(\mathcal X\): a function \(\mu:\Sigma_{\mathcal X}\to\mathbb R\) that satisfies
- \(\mu(B)\geq0\) for all \(B\in\Sigma_{\mathcal X}\)
- \(\mu(\varnothing)=0\)
- countable additivity
- a probability measure: \(\mu(\mathcal X)=1\)
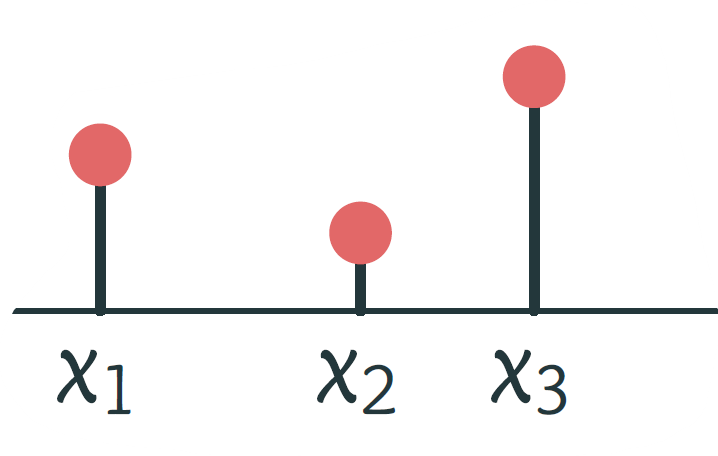
A "continuous" measure \(\mathrm d\mu(x)=f(x)\mathrm dx\).
(has a density w.r.t. the Lebesgue measure \(\mathrm dx\)).
A discrete measure \(\mu=\sum_{i=1}^n a_i\delta_{x_i}\).
Introduction
- measures can represent anything:
point clouds, histograms, 2D images, 3D images, densities of a fluid...

[Monge, 1781], [Kantorovitch, 1942]

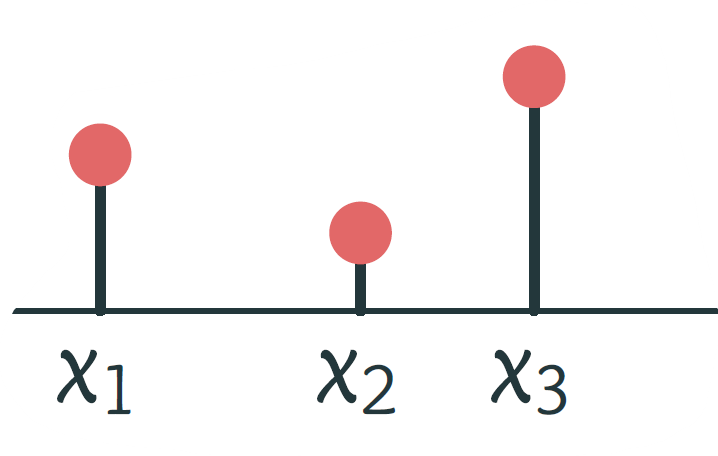
A "continuous" measure \(\mathrm d\mu(x)=f(x)\mathrm dx\).
(has a density w.r.t. the Lebesgue measure \(\mathrm dx\))
A discrete measure \(\mu=\sum_{i=1}^n a_i\delta_{x_i}\).
- pushforward measure \(T_*\mu\), defined as \(T_*\mu(B)\coloneqq \mu(T^{-1}(B))\) for \(T:\mathcal X\to\mathcal Y\)

for a continuous measure:

for a discrete measure:
Introduction

[Monge, 1781], [Kantorovitch, 1942]

- probability measures \(\mu,\nu\in \mathcal P(\mathbb R^n)\)
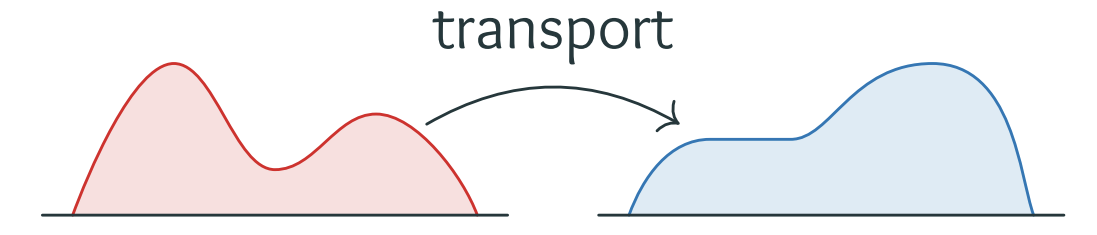
- piles of sand: find strategy \(T\)
OT problem (Monge)
- find the best strategy: cost function \(c:\mathbb R^n\times\mathbb R^n\to\mathbb R\) (e.g. \(\|x-y\|^2\))
Optimal transport

OT problem (Monge)
[Monge, 1781], [Kantorovitch, 1942]

- \(\mathcal X\) and \(\mathcal Y\) Polish spaces
- \(\mu\in\mathcal P(\mathcal X),\, \nu\in\mathcal P(\mathcal Y)\)
- cost function \(c:\mathcal X\times\mathcal Y\to\mathbb R\)
Optimal transport

graph of \(T\): \[\big\{(x,T(x))\mid x\in\mathcal X\big\}\subset \mathcal X\times\mathcal Y\]

OT problem (Monge)
OT problem (Kantorovitch)
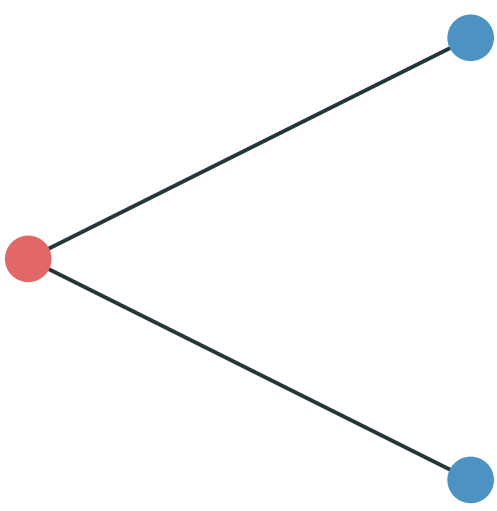
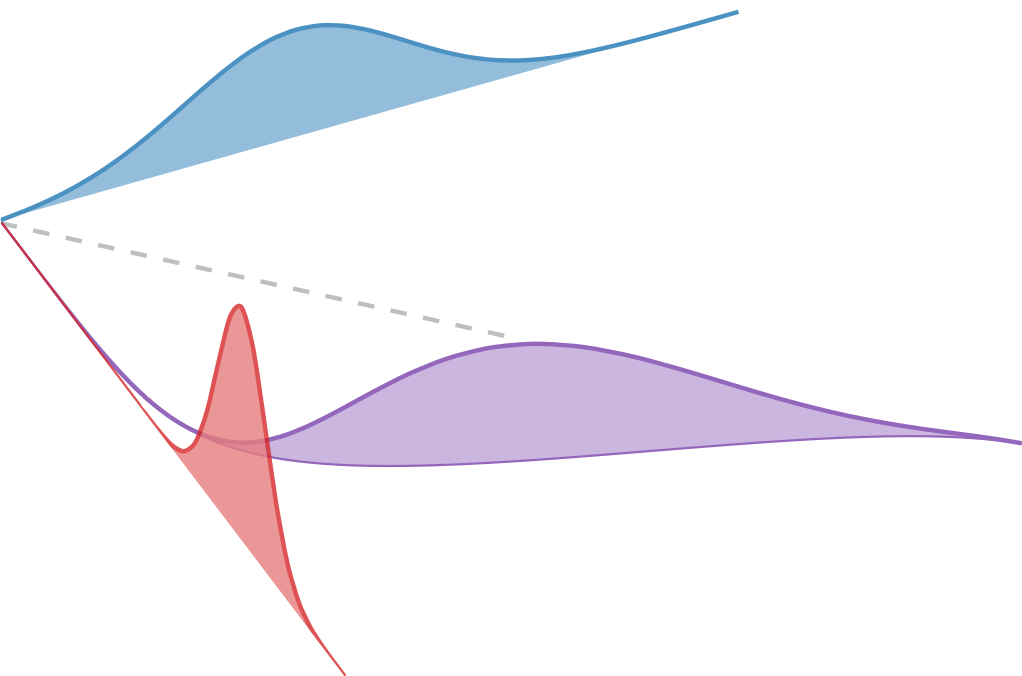
not feasible by a map!

\(\pi\) is induced by a transport map \(T\)
\(\pi\) is a transport plan
relaxation
[Monge, 1781], [Kantorovitch, 1942]

- \(\mathcal X\) and \(\mathcal Y\) Polish spaces
- \(\mu\in\mathcal P(\mathcal X),\, \nu\in\mathcal P(\mathcal Y)\)
- cost function \(c:\mathcal X\times\mathcal Y\to\mathbb R\)
Optimal transport

OT problem (Kantorovitch)
[Monge, 1781], [Kantorovitch, 1942]

- \(\mathcal X\) and \(\mathcal Y\) Polish spaces
- \(\mu\in\mathcal P(\mathcal X),\, \nu\in\mathcal P(\mathcal Y)\)
- cost function \(c:\mathcal X\times\mathcal Y\to\mathbb R\)
- the set of transport plans is non-empty (always \(\mu\otimes\nu\)), so existence of minimizers!
- linear program in \(\pi\): easy to solve!
- if \(c(x,y)=\|x-y\|^p_2\): \(p\)-Wasserstein distance (sometimes Earth Mover Distance)
Optimal transport

Brenier's theorem
When \(\mathcal X=\mathcal Y=\mathbb R^n\) and \(c(x,y)=\|x-y\|^2\), if \(\mu\ll\mathrm dx\), then there is a unique solution to (KP), and it is induced by a map \(T=\nabla f\) with \(f:\mathbb R^n\to\mathbb R\) convex.


relaxation
\(\pi\) is induced by a transport map \(T\)
\(\pi\) is a transport plan
Monge (maps)
Kantorovitch (plans)
[Brenier, 1987]
Can we say that the solution of (KP) is a map?
?
generalizations to complete Riemannian manifolds \(\mathcal X\) and \(\mathcal Y\) and other cost functions \(c\)?
?
Optimal transport

2. Optimal maps for OT
Yann Brenier


Robert McCann

Cédric Villani

Map solutions of OT
Twist condition
We say that \(c\) satisfies the twist condition if
\[\text{for all }x_0\in\mathcal X,\quad y\mapsto \nabla_x c(x_0,y)\in T_{x_0}\mathcal X \text{ is injective.}\]
Suppose this is satisfied. If \(\mu \ll \mathrm dx\), then (KP) admits a unique solution and it is supported on the graph of a map which is the gradient of a \(c\)-convex function \(f:\mathcal X\to\mathbb{R}\):
\[\pi^\star=(\text{id},c\text{-}\exp_x(\nabla f))_*\mu.\]
[Gangbo, 1996], [Villani, 2008], [McCann and Guillen, 2011]
- Examples:
- \(\|x-y\|^2\) in \(\mathbb R^n\)
- \(\langle x,y\rangle\) in \(\mathbb R^n\)
- \(\langle x,y\rangle\) on \(\mathbb S^{n-1}\)



- \(c\)-\(\exp_x(p)\) is the unique \(y\) satisfying \(\nabla_xc(x,y)+p=0\).
- usual Riemannian exp when \(c=d^2/2\).
Map solutions of OT

Map solutions of OT
Twist condition
We say that \(c\) satisfies the twist condition if
\[\text{for all }x_0\in\mathcal X,\quad y\mapsto \nabla_x c(x_0,y)\in T_{x_0}\mathcal X \text{ is injective.}\]
Suppose this is satisfied. If \(\mu \ll \mathrm dx\), then (KP) admits a unique solution and it is supported on the graph of a map which is the gradient of a \(c\)-convex function \(f:\mathcal X\to\mathbb{R}\):
\[\pi^\star=(\text{id},c\text{-}\exp_x(\nabla f))_*\mu.\]
[Gangbo, 1996], [Villani, 2008], [McCann and Guillen, 2011]
- Examples:
- \(\|x-y\|^2\) in \(\mathbb R^n\)
- \(\langle x,y\rangle\) in \(\mathbb R^n\)
- \(\langle x,y\rangle\) on \(\mathbb S^{n-1}\)



- \(c\)-\(\exp_x(p)\) is the unique \(y\) satisfying \(\nabla_xc(x,y)+p=0\).
- usual Riemannian exp when \(c=d^2/2\).

Subtwist condition
We say that \(c\) satisfies the subtwist condition if
\[\text{for all }y_1\neq y_2,\quad x\mapsto c(x,y_1)-c(x,y_2)\text{ has at most 2 critical points.}\]
Suppose this is satisfied. If \(\mu \ll \mathrm dx\), then (KP) admits a unique solution and it is supported on the union of a graph and an anti-graph:
\[\pi^\star=(\text{id},G)_*\bar \mu+(H,\text{id})_*(\nu- G_*\bar\mu).\]
- Examples:
- \(\|x-y\|^2\) in \(\mathbb R^n\)
- \(\langle x,y\rangle\) in \(\mathbb R^n\)
- \(\langle x,y\rangle\) on \(\mathbb S^{n-1}\)



[Ahmad et al., 2011], [Chiappori et al., 2010]
Map solutions of OT

Subtwist condition
We say that \(c\) satisfies the subtwist condition if
\[\text{for all }y_1\neq y_2,\quad x\mapsto c(x,y_1)-c(x,y_2)\text{ has at most 2 critical points.}\]
Suppose this is satisfied. If \(\mu \ll \mathrm dx\), then (KP) admits a unique solution and it is supported on the union of a graph and an anti-graph:
\[\pi^\star=(\text{id},G)_*\bar \mu+(H,\text{id})_*(\nu- G_*\bar\mu).\]
- Examples:
- \(\|x-y\|^2\) in \(\mathbb R^n\)
- \(\langle x,y\rangle\) in \(\mathbb R^n\)
- \(\langle x,y\rangle\) on \(\mathbb S^{n-1}\)



[Ahmad et al., 2011], [Chiappori et al., 2010]
Map solutions of OT

\(m\)-twist condition
We say that \(c\) satisfies the \(m\)-twist condition if
\[\text{for all }x_0, y_0,\quad \text{card}\{y\mid \nabla_x c(x_0,y)=\nabla_x c(x_0,y_0)\}\leq m.\]
Suppose this is satisfied and \(c\) is bounded. If \(\mu \ll \mathrm dx\), then optimals plans of (KP) are supported on the graphs of \(m\) maps:
\[\pi^\star=\sum_{i=1}^m\alpha_i (\text{id},T_i)_* \mu.\]
in the sense \(\pi^\star(S)=\sum_i \int_{\mathcal X}\alpha_i(x)\chi_S(x,T_i(x))\,\mathrm d\mu\) for any Borel \(S\subset \mathcal X\times \mathcal Y\).
[Moameni, 2016]
Map solutions of OT

\(m\)-twist condition
We say that \(c\) satisfies the \(m\)-twist condition if
\[\text{for all }x_0, y_0,\quad \text{card}\{y\mid \nabla_x c(x_0,y)=\nabla_x c(x_0,y_0)\}\leq m.\]
Suppose this is satisfied and \(c\) is bounded. If \(\mu \ll \mathrm dx\), then optimals plans of (KP) are supported on the graphs of \(m\) maps:
\[\pi^\star=\sum_{i=1}^m\alpha_i (\text{id},T_i)_* \mu.\]
in the sense \(\pi^\star(S)=\sum_i \int_{\mathcal X}\alpha_i(x)\chi_S(x,T_i(x))\,\mathrm d\mu\) for any Borel \(S\subset \mathcal X\times \mathcal Y\).
[Moameni, 2016]
Map solutions of OT

twist
map
\(\implies\)
subtwist
map/anti-map
\(\implies\)
\(m\)-twist
\(m\)-map
\(\implies\)
(for simplicity, when \(\mu\ll\mathrm dx\) and \(\mu,\nu\) have compact support)
for linear OT problem:
Map solutions of OT

3. Optimal maps for Gromov-Wasserstein
Karl-Theodor Sturm
Facundo Mémoli


Mikhaïl Gromov


[Sturm, 2012]
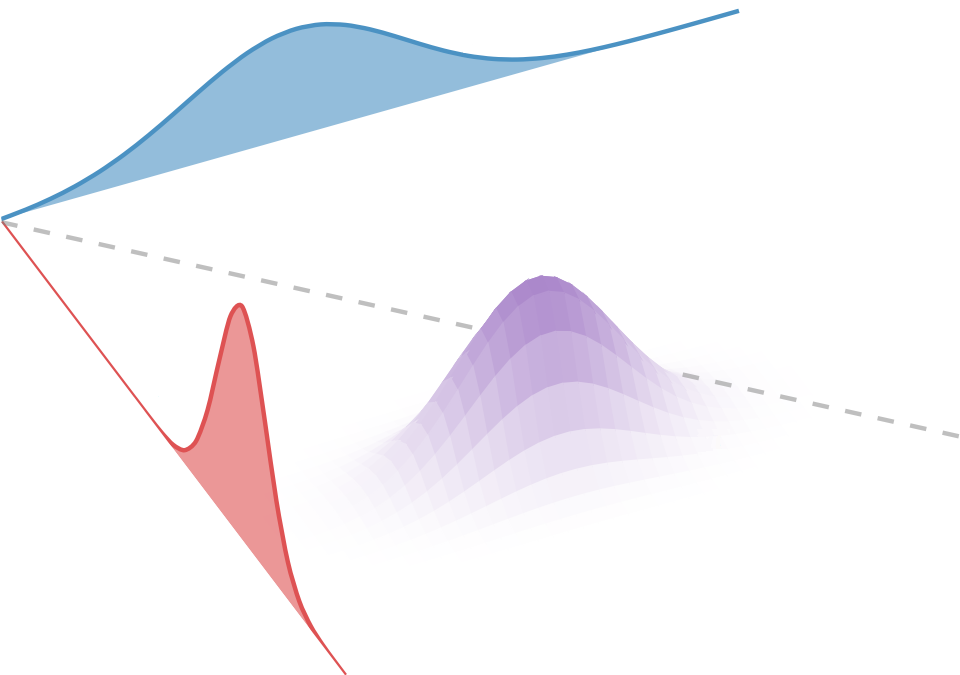
Wasserstein:

Gromov-Wasserstein:
cost function
\(c:\mathcal X\times\mathcal Y\to\mathbb R\)
cost functions
\(c_{\mathcal X}:\mathcal X\times\mathcal X\to\mathbb R\)
\(c_{\mathcal Y}:\mathcal Y\times\mathcal Y\to\mathbb R\)
The Gromov-Wasserstein problem

The Gromov-Wasserstein problem
[Sturm, 2012]
GW problem
- distance modulo isometries: not really transport but rather correspondence
- applications: invariance by isometries + measures living in different spaces
- quadratic in \(\pi\)! \(\implies\) hard to solve
?
optimal plans = maps?


[Alvares-Melis et al., 2019], [Vayer, 2020], [Sturm, 2012], [D., Lacombe & Vialard, 2023]
\(\mu\ll\mathrm dx\) and \(\mu,\nu\) with compact support
There is an optimal map!
There is an optimal 2-map!
(i) Inner product case, \(c_{\mathcal X}=c_{\mathcal Y}=\langle\cdot,\cdot\rangle\)
(ii) Squared distance case, \(c_{\mathcal X}=c_{\mathcal Y}=\|\cdot-\cdot\|^2\)
\(\mathcal X=\mathcal Y=\mathbb R^n\)
?
Can we simply apply the twist conditions? No....
for linear OT problems:
Optimal maps for GW

quadratic
Optimal maps for GW
symmetric
bilinear
Idea: relax into linear problem and try to apply twist conditions
[D., Lacombe & Vialard, 2023]
First order optimality condition:
\(\pi^\star\) minimizes \(\pi\mapsto F(\pi,\pi)\) \(\pi^\star\) minimizes \(\pi\mapsto 2F(\pi,\pi^\star)\)
Good news: we now have a OT problem with cost \(C_{\pi^\star}\)!
:)
twist conditions for \(C_{\pi^\star}\)? not always, need something more general
:(

[D., Lacombe & Vialard, 2023]
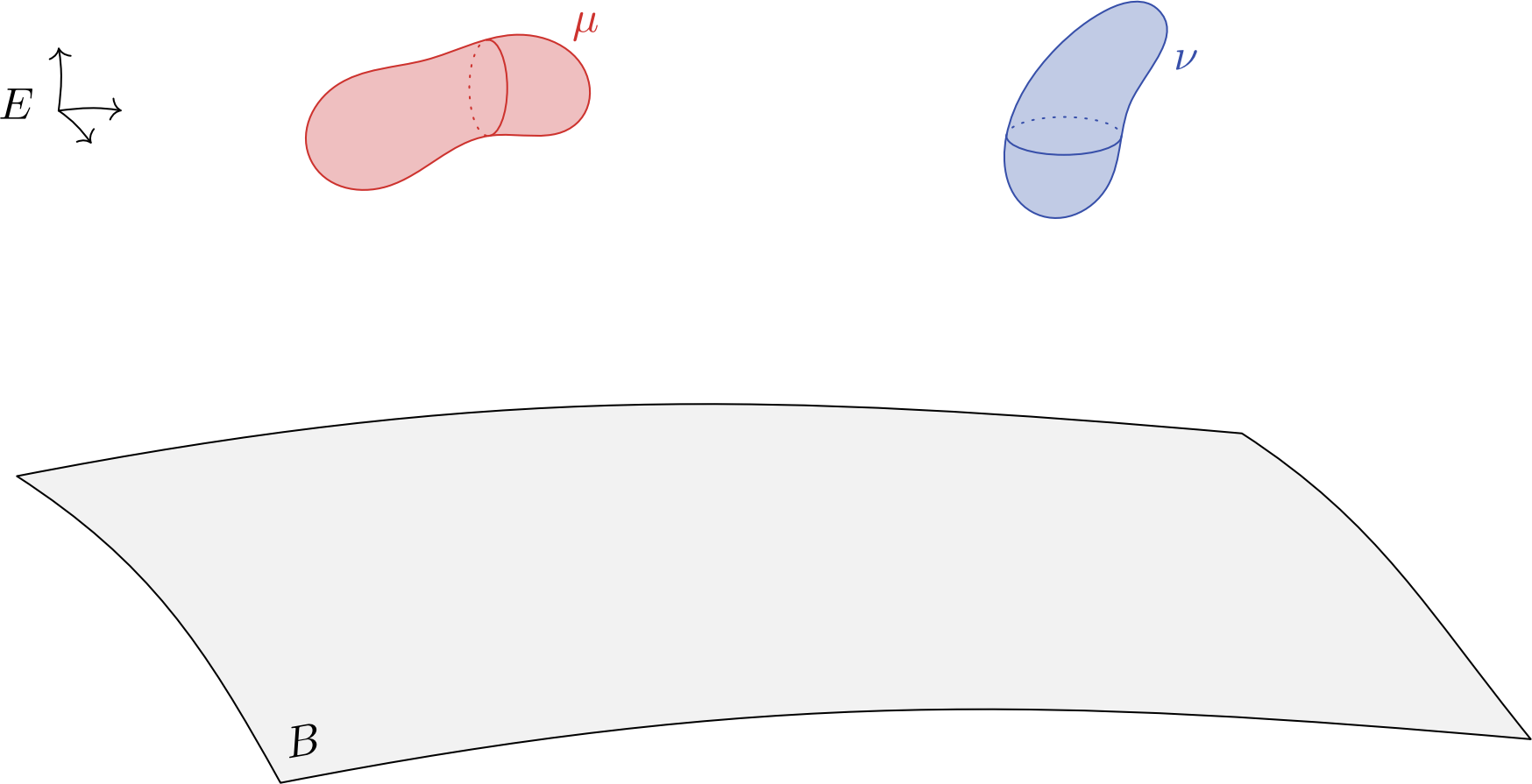
"Let \(\mu,\nu\in\mathcal P(E)\).
A more general twist condition

[D., Lacombe & Vialard, 2023]
"Let \(\mu,\nu\in\mathcal P(E)\). If we can send \(\mu\) and \(\nu\) in a space \(B\) by a map \(\varphi:E\to B\),
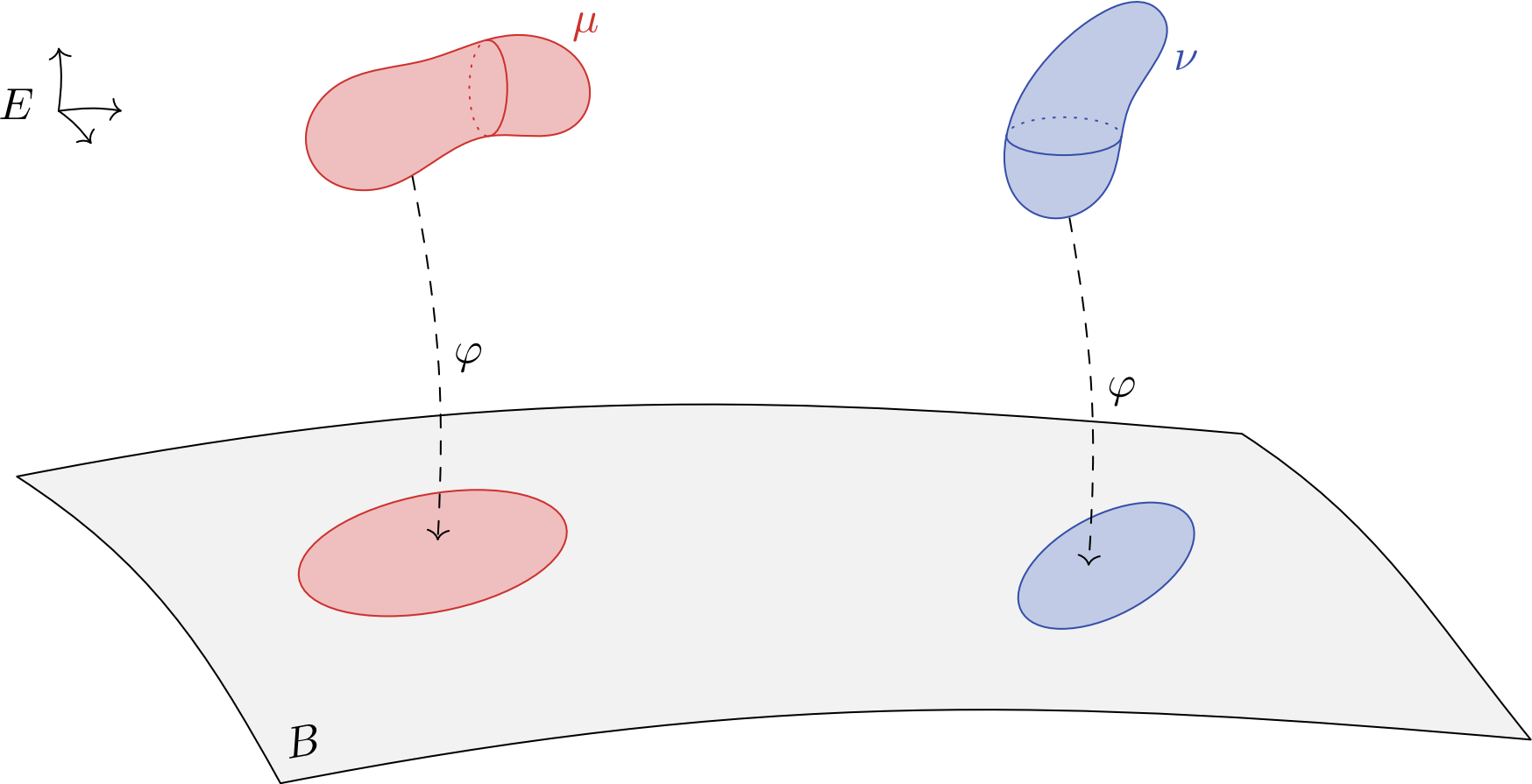
A more general twist condition

[D., Lacombe & Vialard, 2023]
"Let \(\mu,\nu\in\mathcal P(E)\). If we can send \(\mu\) and \(\nu\) in a space \(B\) by a map \(\varphi:E\to B\), such that \[c(x,y)=\tilde c(\varphi(x),\varphi(y))\quad\text{for all }x,y\in E\] with \(\tilde c\) a twisted cost on \(B\),
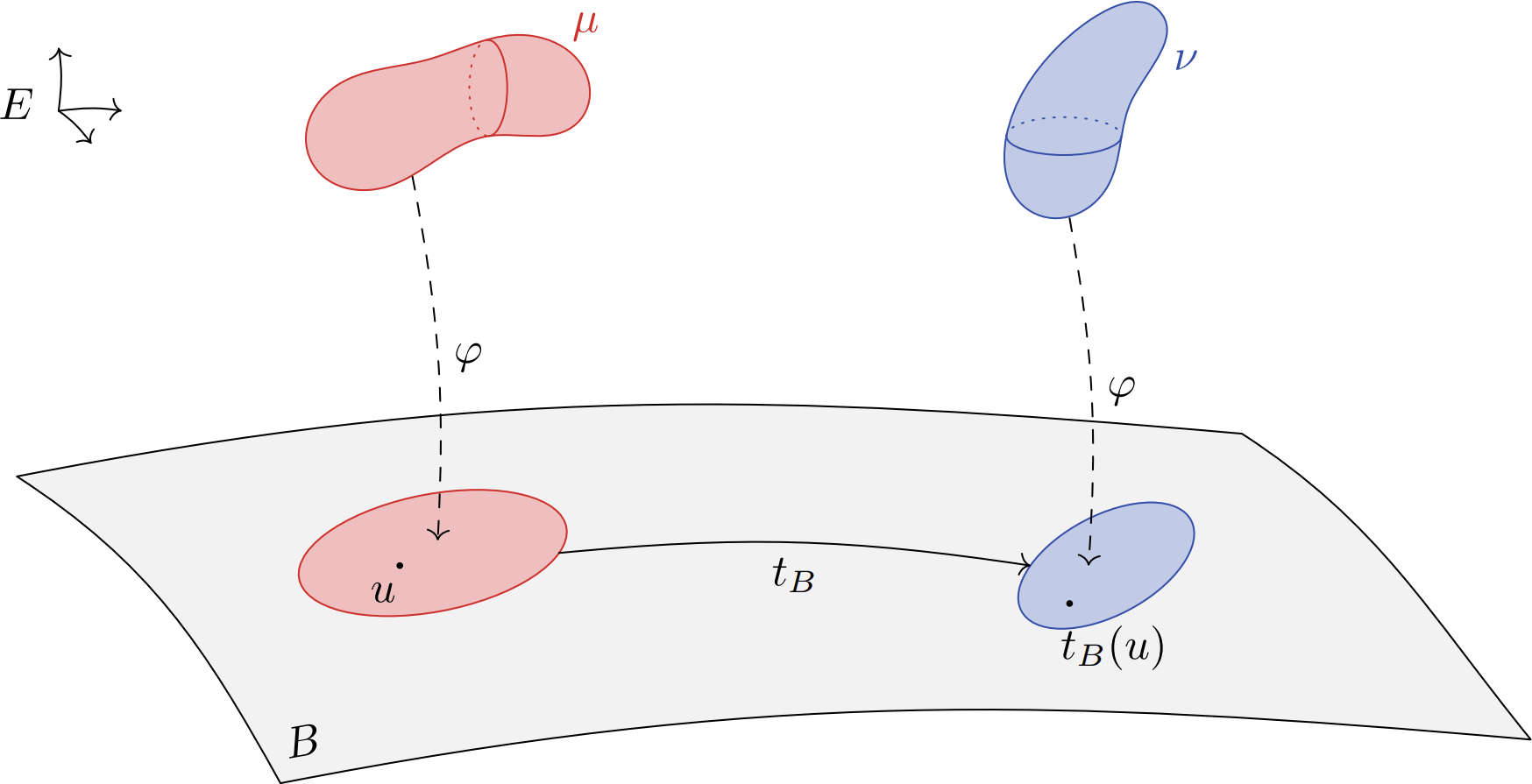
A more general twist condition

[D., Lacombe & Vialard, 2023]
"Let \(\mu,\nu\in\mathcal P(E)\). If we can send \(\mu\) and \(\nu\) in a space \(B\) by a map \(\varphi:E\to B\), such that \[c(x,y)=\tilde c(\varphi(x),\varphi(y))\quad\text{for all }x,y\in E\] with \(\tilde c\) a twisted cost on \(B\), then we can construct an optimal map between \(\mu\) and \(\nu\)."
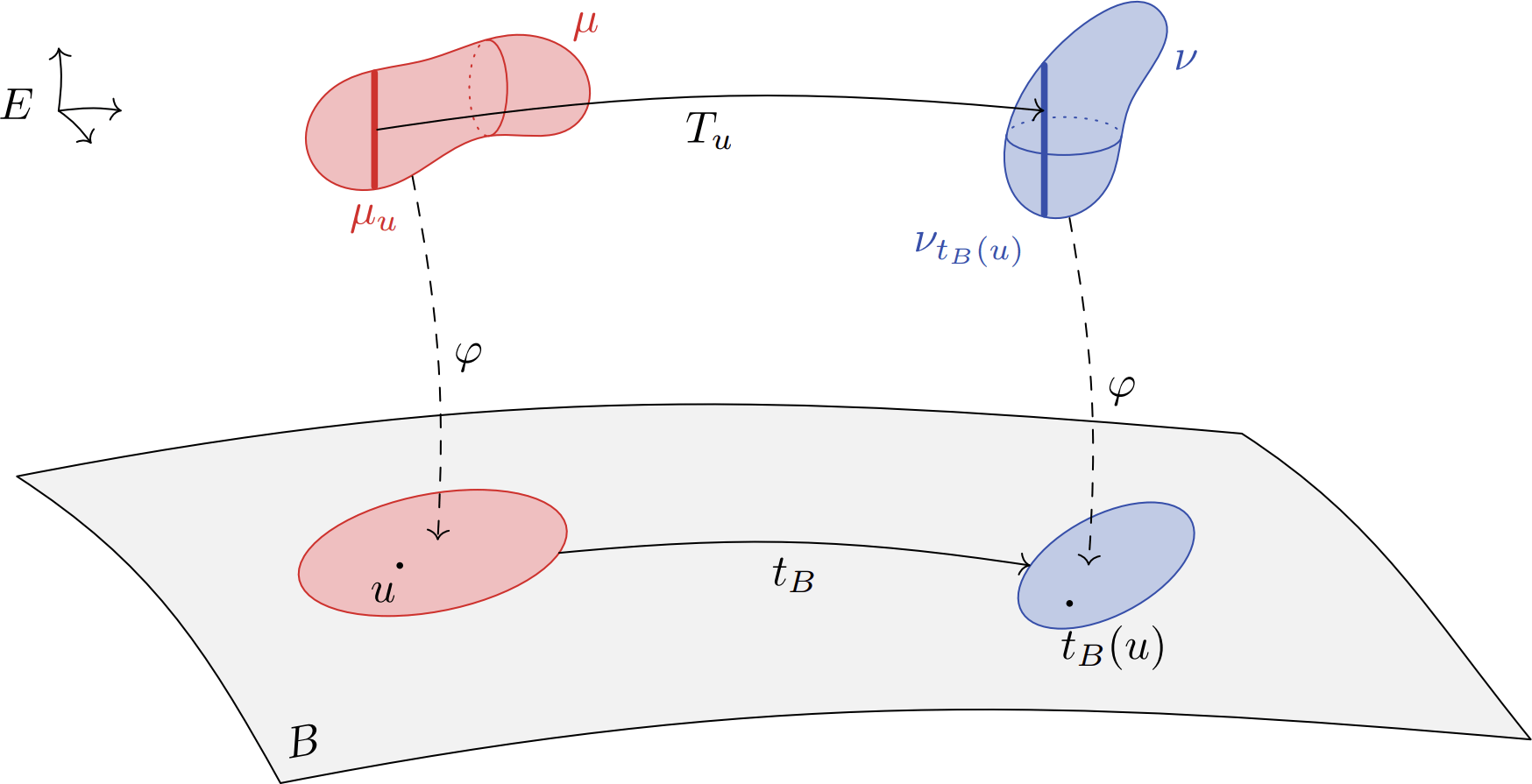
A more general twist condition

[D., Lacombe & Vialard, 2023]

A more general twist condition

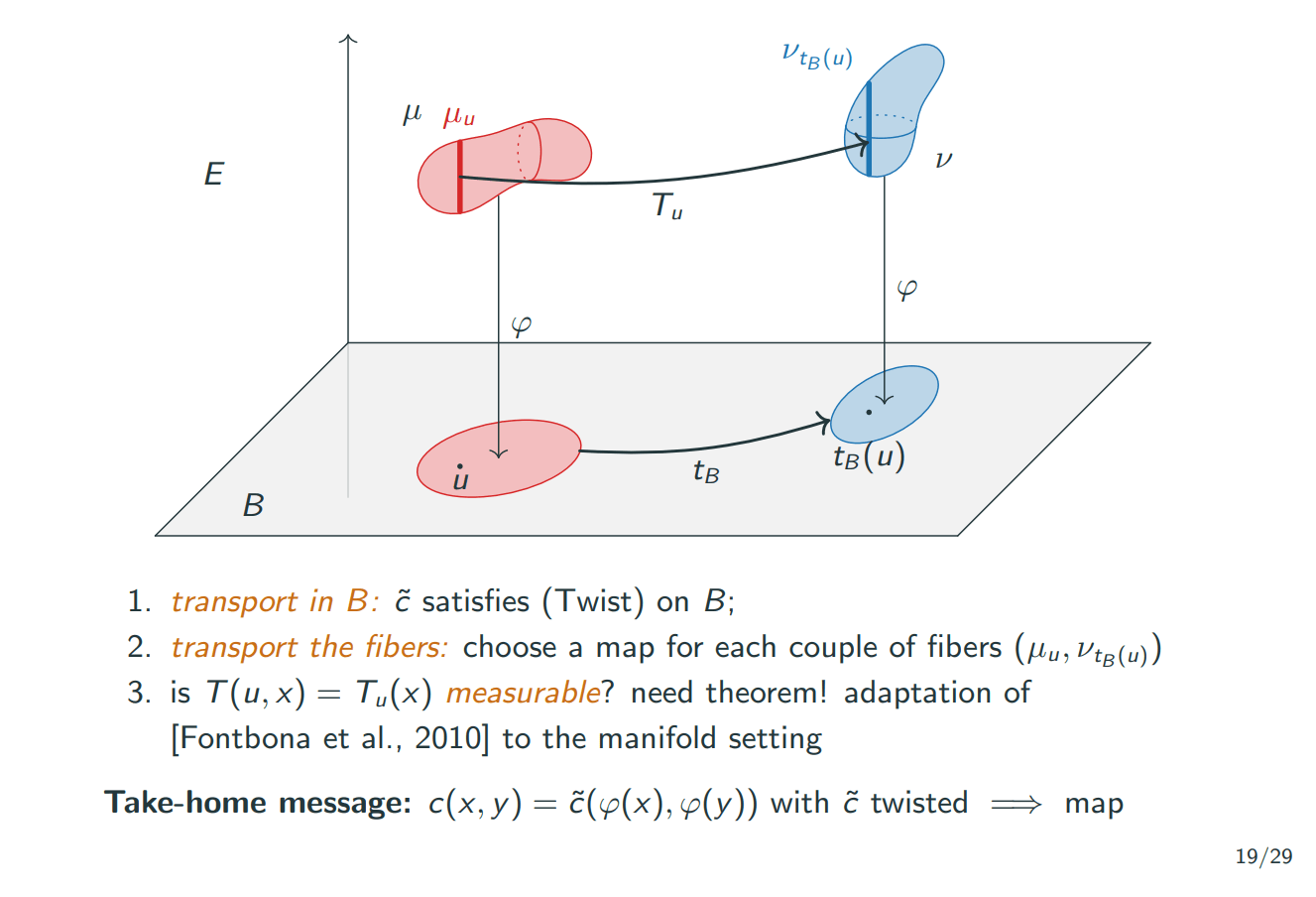
A more general twist condition

twist
map
\(\implies\)
subtwist
map/anti-map
\(\implies\)
\(m\)-twist
\(m\)-map
\(\implies\)
(for simplicity, when \(\mu\ll\mathrm dx\) and \(\mu,\nu\) have compact support)
A more general twist condition
our general condition
for linear OT problem:

[D., Lacombe & Vialard, 2023]
(i) Inner product case, \(c_{\mathcal X}=c_{\mathcal Y}=\langle\cdot,\cdot\rangle\)
OT problem with cost
\(C_{\pi^\star}(x,y)=-\langle M^\star x,y\rangle\)
where \(M^\star=\int x'y'^\top\,\mathrm d\pi(x',y')\)
\(\implies\)
\(\implies\)
satisfies our general condition
\(\implies\)
there exists an optimal map
\(\mu\ll\mathrm dx\) and \(\mu,\nu\) with compact support
\(\mathcal X=\mathcal Y=\mathbb R^n\)
linearize
- up to a SVD, suppose that \(M^\star\) is a diagonal matrix of singular values: \[M^\star=\begin{pmatrix}\sigma_1 & & & & & \\ & \ddots & & & & &\\& & \sigma_h & & &\\ & & & 0 & & \\ & & & & \ddots &\\ & & & & & 0 \end{pmatrix}\]
- rephrase the cost: \[c(x,y)=-\langle M^\star x,y\rangle=-\sum_{i=1}^h\sigma_i x_iy_i=\tilde c(p(x),p(y))\] with \(p\) the orthogonal projection on \(\mathbb R^h\)
- check if \(\tilde c\) is twisted: it is!
+ some structure!
\(T(u,v)=(\nabla f\circ M^\star(u), \nabla g_u(v))\)
Does it satisfy our general condition?
Optimal maps for GW

Optimal maps for GW
[D., Lacombe & Vialard, 2023]
(i) Inner product case, \(c_{\mathcal X}=c_{\mathcal Y}=\langle\cdot,\cdot\rangle\)
(ii) Squared distance case, \(c_{\mathcal X}=c_{\mathcal Y}=\|\cdot-\cdot\|^2\)
OT problem with cost
\(C_{\pi^\star}(x,y)=-\langle M^\star x,y\rangle\)
where \(M^\star=\int x'y'^\top\,\mathrm d\pi(x',y')\)
\(\implies\)
\(\implies\)
satisfies our general condition
\(\implies\)
there exists an optimal map
OT problem with cost
\(C_{\pi^\star}(x,y)=-\|x\|^2\|y\|^2-4\langle M^\star x,y\rangle\)
where \(M^\star=\int x'y'^\top\,\mathrm d\pi(x',y')\)
\(\implies\)
\(\implies\)
sometimes satisfies our general condition,
sometimes satisfies 2-twist
\(\implies\)
there exists an optimal 2-map
\(\mathcal X=\mathcal Y=\mathbb R^n\)
linearize
linearize
+ if \(\text{rk}(M^\star)\leq n-2\), there exists an optimal map!
\(\mu\ll\mathrm dx\) and \(\mu,\nu\) with compact support

Summary
[D., Lacombe & Vialard, 2023]
There is an optimal map!
There is an optimal 2-map!
(i) Inner product case, \(c_{\mathcal X}=c_{\mathcal Y}=\langle\cdot,\cdot\rangle\)
(ii) Squared distance case, \(c_{\mathcal X}=c_{\mathcal Y}=\|\cdot-\cdot\|^2\)
Conjecture (computational):
this result is tight: there exists cases where no optimal plan is a map
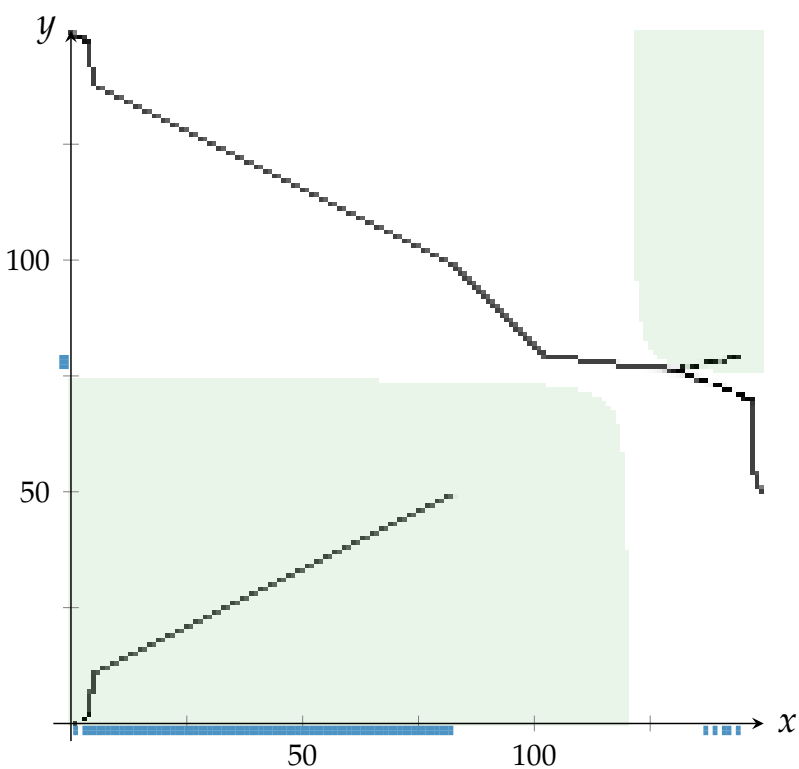
Additional study of 1D case:
- non-optimality of monotone rearrangements in general (additional counter-example)
- optimality of monotone rearrangements in specific cases
\(\mathcal X=\mathcal Y=\mathbb R^n\)
\(\mu\ll\mathrm dx\) and \(\mu,\nu\) with compact support

Ahmad, N., Kim, H. K., and McCann, R. J. (2011). Optimal transportation, topology and uniqueness.
Alvarez-Melis, D., Jegelka, S., and Jaakkola, T. S. (2019). Towards optimal transport with global invariances.
Beinert, R., Heiss, C., and Steidl, G. (2022). On assignment problems related to gromov-wasserstein distances on the real line.
Brenier, Y. (1987). Décomposition polaire et réarrangement monotone des champs de vecteurs
Dumont, T., Lacombe, T., and Vialard, F.-X. (2023). On the Existence of Monge maps for the Gromov-Wasserstein problem.
Fontbona, J., Guérin, H., and Méléard, S. (2010). Measurability of optimal transportation and strong coupling of martingale measures.
Gangbo, W., & McCann, R. J. (1996). The geometry of optimal transportation.
Kantorovich, L. (1942). On the translocation of masses.
McCann, R. J. and Guillen, N. (2011). Five lectures on optimal transportation: geometry, regularity and applications.
Mémoli, F. (2011). Gromov–wasserstein distances and the metric approach to object matching.
Moameni, A. (2016). A characterization for solutions of the monge-kantorovich mass transport problem.
Séjourné, T., Vialard, F.-X., and Peyré, G. (2021). The unbalanced gromov wasserstein distance: Conic formulation and relaxation.
Sturm, K.-T. (2020). The space of spaces: curvature bounds and gradient flows on the space of metric measure spaces.
Vayer, T. (2020). A contribution to optimal transport on incomparable spaces
Villani, C. (2008). Optimal transport: old and new, volume 338.
slides available at https://slides.com/theodumont/monge-gw
•
•
•
•
•
•
•
•
•
•
•
•
•
•
•
References


[D., Lacombe & Vialard, 2023]
There always is an optimal 2-map!
(ii) Squared distance case, \(c_{\mathcal X}=c_{\mathcal Y}=\|\cdot-\cdot\|^2\)
Conjecture (computational):
this result is tight: there exists cases where no optimal plan is a map

\(\mu\ll\mathcal L\) and \(\mu,\nu\) with compact support
\(\mathcal X=\mathcal Y=\mathbb R^n\)
?
Can we say better? i.e.
"There always exists an optimal map"?
- how to exhibit such cases? not so easy, in practice maps are very often optimal.
- in practice, the monotone increasing \(\pi^\oplus_{\text{mon}}\) and decreasing \(\pi^\ominus_{\text{mon}}\) rearrangements are very often optimal
- move away from measures of optimal plans \(\pi^\oplus_{\text{mon}}\) and \(\pi^\ominus_{\text{mon}}\) by gradient descent

Sharpness
