Transfer of entropy inequalities from the classical to the fermionic Boltzmann equation

Lions Magenes days 2024

December 18, 2024

Thomas Borsoni

Laboratoire Jacques-Louis Lions

Context

Distribution of electrons in semi-conductors

Boltzmann-Fermi-Dirac equation

In physics:

Evolution equation:

\partial_t f = Q(f)

(homogeneous)

Existence of equilibrium state

(Boltzmann for fermions)

Motivation

Explicit rate of relaxation to equilibrium for sol. to Boltzmann-Fermi-Dirac eq.

Main result

entropy ineq.

classical molecules

entropy ineq.

fermions

Means

Entropy methods

-> functional inequalities

\implies

known

new!

Outline​

1. Quantum Boltzmann for fermions

3. Transfer of entropy inequalities

2. Entropy methods

the classical boltzmann equation

1. Quantum Boltzmann for fermions

\partial_t f_t(v) = Q_0(f_t)(v),

(homogeneous)

(B)

where

Q_{0}(f)(v) = \int \left[f(v') f(v'_*) - f(v) f(v_*) \right] B

Features:

  • symmetry, reversibility
  • conserves of mass, momentum, energy
  • decrease of classical entropy
v
v_*
v'
v'_*
v

Equilibrium: Maxwellian

M_0

the boltzmann-Fermi-Dirac equation

1. Quantum Boltzmann for fermions

  • quantum parameter \(\varepsilon \propto \hbar^3\)
\partial_t f_t(v) = Q_{\color{purple}\varepsilon}(f_t)(v),

(homogeneous)

(BFD)

where

Q_{\color{purple} \varepsilon}(f)(v) = \int \left[f' f'_* \textcolor{purple}{(1 - \varepsilon f) (1-\varepsilon f_*)} - f f_* \textcolor{purple}{(1 - \varepsilon f')(1-\varepsilon f'_*)} \right] B

Features:

  • symmetry, reversibility
  • conserves of mass, momentum, energy
  • decrease of Fermi entropy

Equilibrium: Fermi-Dirac statistics

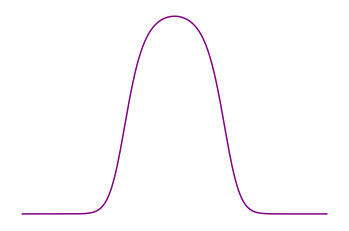
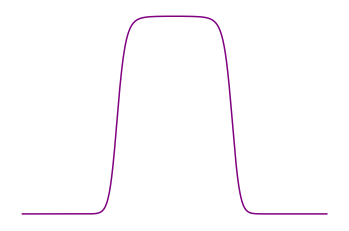
(+ saturated state)

  • \(\displaystyle 0 \leq f_t \leq \frac{1}{\varepsilon} \)

Boltzmann + Pauli's exclusion principle

M_{\varepsilon}

relaxation to equilibrium, entropy methods

- Relative entropy to equilibrium, general setting

 

 

- Entropy inequalities results

Equilibrium and entropy

\partial_t f_t = Q(f_t)

(generically)

relative entropy to equilibrium

H(g|M^g) \geq 0
H(g) - H(M^g) =:

Generically, \(H\) is an entropy and \(M\) is a thermodynamical equilibrium when:

  • \(t  \mapsto H(f_t)\) is nonincreasing
  • \(M\) minimizes \(H\) under some constraints (mass, energy...)

used to quantify distance to equilibrium

2. Relaxation to equilibrium, entropy methods

entropy methods

\partial_t f_t = Q(f_t)

Entropy dissipation \(D\)

\displaystyle \frac{\mathrm{d}}{\mathrm{d} t} H(f_t) = - D(f_t)

\(D \) non-negative operator

Try to prove \(D(f) \gtrsim H(f|M^{f})^{1+\delta}\)

(functional inequality)

Entropy method

To obtain \(H(f_t|M^{f_0}) \lesssim t^{-1/\delta}\)

\displaystyle \frac{\mathrm{d}}{\mathrm{d} t} H(f_t|M^{f_0}) = - D(f_t)

Try to prove \(D(f) \gtrsim H(f|M^{f})\)

To obtain \(H(f_t|M^{f_0}) \lesssim e^{-Ct} \)

(Grönwall)

2. Relaxation to equilibrium, entropy methods

Entropy inequalities results

D_0(g) \gtrsim H_0(g|M_0^g)^{1 + \delta}

classical Boltzmann

D_{\varepsilon}(f) \gtrsim H_{\varepsilon}(f|M^{f}_{\varepsilon})^{1+\delta}

Boltzmann-FERMI-DIRAC

Toscani, Villani

?

2. Relaxation to equilibrium, entropy methods

\(D_0\): classical entropy dissipation

\(H_0\): classical entropy

\(D_\varepsilon\): Fermi-Dirac entropy dissipation

\(H_\varepsilon\): Fermi-Dirac entropy

Obtention of entropy inequalities for Boltzmann-Fermi-Dirac

- Transfer of ineq. from classical to quantum

 

 

 

- Application to the Boltzmann-Fermi-Dirac equation

a first remark

If \(1- \varepsilon f \geq \kappa_0 \), then 

\displaystyle D_{\varepsilon}(f) \gtrsim D_{0}\left( \frac{f}{1 - \varepsilon f} \right).

3. Relaxation to equilibrium for fermionic Boltzmann: a method of transfer

\kappa_0 \in (0,1)

Fermi-Dirac entropy dissipation of  \(f\)

Classical entropy dissipation of \(\displaystyle \frac{f}{1-\varepsilon f}\)

Transfer of inequalities

D_0(g) \gtrsim H_0(g|M_0^g)^{1 + \delta}
D_{\varepsilon}(f)
H_{\varepsilon}(f|M^f_{\varepsilon})^{1 + \delta}

we know:

we want to prove:

D_{\varepsilon}(f) \gtrsim D_{0}\left(\frac{f}{1 - \varepsilon f}\right)
\gtrsim \; \; D_{0}\left(\frac{f}{1 - \varepsilon f}\right)
\gtrsim

?

entropy inequality for classical Boltzmann

D_{\varepsilon}(f) \gtrsim H_{\varepsilon}(f|M^f_{\varepsilon})^{1 + \delta}

Fermi-Dirac dissipation of \(f\)

\( \gtrsim\) classical dissipation of \( \displaystyle \frac{f}{1-\varepsilon f} \)

\gtrsim \; \; H_0 \left(\frac{f}{1- \varepsilon f} \left|M_0^{\frac{f}{1- \varepsilon f}} \right. \right)^{1 + \delta}

entropy inequality for fermionic Boltzmann

3. Relaxation to equilibrium for fermionic Boltzmann: a method of transfer

(Toscani, Villani)

Comparison of relative entropies

H_{0}\left(\left.\frac{f}{1 - \varepsilon f}\right|M^{\frac{f}{1 - \varepsilon f}}_{0}\right) \geq H_{\varepsilon}(f|M^f_{\varepsilon}).

H: whenever all terms make sense

Classical relative entropy to equilibrium of  \(\displaystyle \frac{f}{1-\varepsilon f}\)

Fermi relative entropy to equilibrium of \(f\)

Theorem.

f \in L^1_2(\R^3)
\frac{f}{1 - \varepsilon f} \in L^1_2(\R^3) \cap L \log L(\R^3),
\displaystyle 0 \leq f < \frac{1}{\varepsilon}

For all

such that

and

3. Relaxation to equilibrium for fermionic Boltzmann: a method of transfer

Proof

R_g(\varepsilon) = H_{\varepsilon}\left( \varphi_{\varepsilon}^{-1}(g) \left|M^{\varphi_{\varepsilon}^{-1}(g)}_{\varepsilon} \right. \right).

Let, for \(\varepsilon \geq 0\),

Then \(R_g\) is decreasing on \(\R_+\).

Proposition.

Key elements of the proof:

  • Taylor representation of relative entropy (general form)
  • differentiation of \(R_g\) in \(\varepsilon\)
  • "magical" cancellations due to the general links entropy/equilibria

Other technicalities:

  • differentiability of \(R_g \) on \(\R_+^*\)
  • continuity of \(R_g \) at \(0\)

general considerations

specific use of Fermi-Dirac features

\varphi_{\varepsilon}(x) = \frac{x}{1 - \varepsilon x}

3. Relaxation to equilibrium for fermionic Boltzmann: a method of transfer

R_g(0) = H_{0}\left(\left.\frac{f}{1 - \varepsilon f}\right|M^{\frac{f}{1 - \varepsilon f}}_{0}\right)
g = \frac{f}{1 - \varepsilon f},
R_g(\varepsilon) =H_{\varepsilon}(f|M^f_{\varepsilon})

take

\geq

then

\&

Conclusion

D_0(g) \geq C_g \, H_0(g|M_0^g)^{1 + \delta}
D_{\varepsilon}(f) \geq \kappa_0^4 \, C_{\frac{f}{1-\varepsilon f}} H_{\varepsilon}(f|M_{\varepsilon}^f)^{1 + \delta}

entropy inequality for classical Boltzmann

entropy inequality for fermionic Boltzmann

(1 - \varepsilon f \geq \kappa_0)

counter-example for classical Boltzmann (Bobylev, Cercignani)

counter-example for fermionic Boltzmann

3. Relaxation to equilibrium for fermionic Boltzmann: a method of transfer

Convergence to equilibrium

Proof of algebraic convergence to equilibrium

with B. Lods

\|f_t-M_{\varepsilon}\|_{L^p_k} \leq C \, (1+t)^{- \eta/p}

\(p \in [1,\infty), \, k \geq 0\), and with \(C,\eta\)  explicit.

(Boltzmann-Fermi-Dirac homogeneous cut-off hard potentials)

Thank you for your attention!