Entropy methods

for the fermionic Boltzmann equation

Thomas Borsoni*

Journées Jeunes EDPistes de France

January 15, 2026

*postdoc at CERMICS, École Nationale des Ponts et Chaussées

Supervised by V. Ehrlacher & T. Lelièvre

Outline​

  The classical and fermionic Boltzmann equations

Trend to equilibrium

Introduction

 1. The entropy method

 2. Overview for kinetic equations

 3. Transfer from classical to fermionic

  The classical and fermionic Boltzmann equations

Trend to equilibrium

Introduction

 1. The entropy method

 2. Overview for kinetic equations

 3. Transfer from classical to fermionic

(\partial_t + v \cdot \nabla_x) g_{t,x}(v) = Q(g_{t,x})(v)

\(g \equiv g_{t,x}(v)\) density of molecules

+
x

the classical Boltzmann equation

v

Boltzmann equation:

v
v_*
v'
v'_*
\begin{align*} v+v_*&=v'+v'_* \\ \frac12|v|^2 + \frac12|v_*|^2 &= \frac12|v'|^2 + \frac12|v'_*|^2 \\ \end{align*}

Conservation laws

Collision operator:

\newcommand{\dd}{\mathrm{d}} Q_{\textcolor{green}{0}}(g)(v) = \iint_{\R^3 \times \mathbb{S}^2} [g(v') g(v'_*) - g(v) g(v_*)] \; B \; \dd v_* \, \dd \sigma
\begin{align*} v' = \frac{v+v_*}{2} + \frac{|v-v_*|}{2} \; \sigma \\ v'_* = \frac{v+v_*}{2} - \frac{|v-v_*|}{2} \; \sigma\\ \end{align*}
\newcommand{\Sb}{\mathbb{S}} \sigma \in \Sb^2
\implies

(momentum)

(energy)

     \(B \equiv B(v,v_*, \sigma) > 0 \)  \(\leftrightarrow\)   interaction potential

Collision kernel:

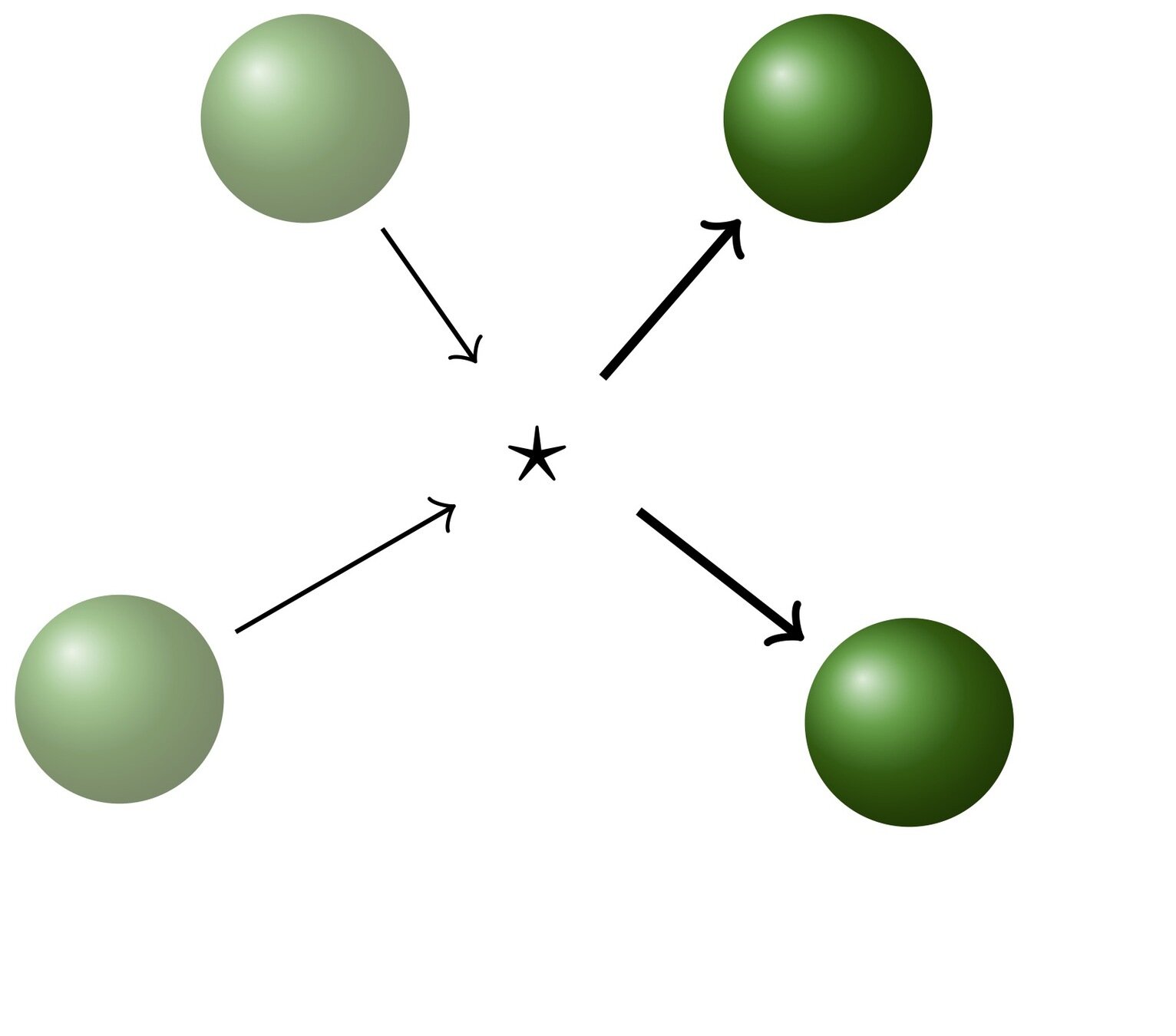
Statistical description of a rarefied monoatomic gas

\partial_t g_{t}(v) = Q_{\textcolor{green}{0}}(g_{t})(v)

\(g \equiv g_{t}(v)\) density of molecules

+
x

the space-homogeneous

classical Boltzmann equation

v
  • Boltzmann equation
v
v
\textcolor{blue}{u}
\textcolor{blue}{\sqrt{T}}
M^{g_0}_{\textcolor{green}{0}}(v) = \textcolor{blue}{\rho}\, (2 \pi \textcolor{blue}{T})^{-\frac32} \, \exp \left(-\frac{|v-\textcolor{blue}{u}|^2}{2 \, \textcolor{blue}{T}} \right)
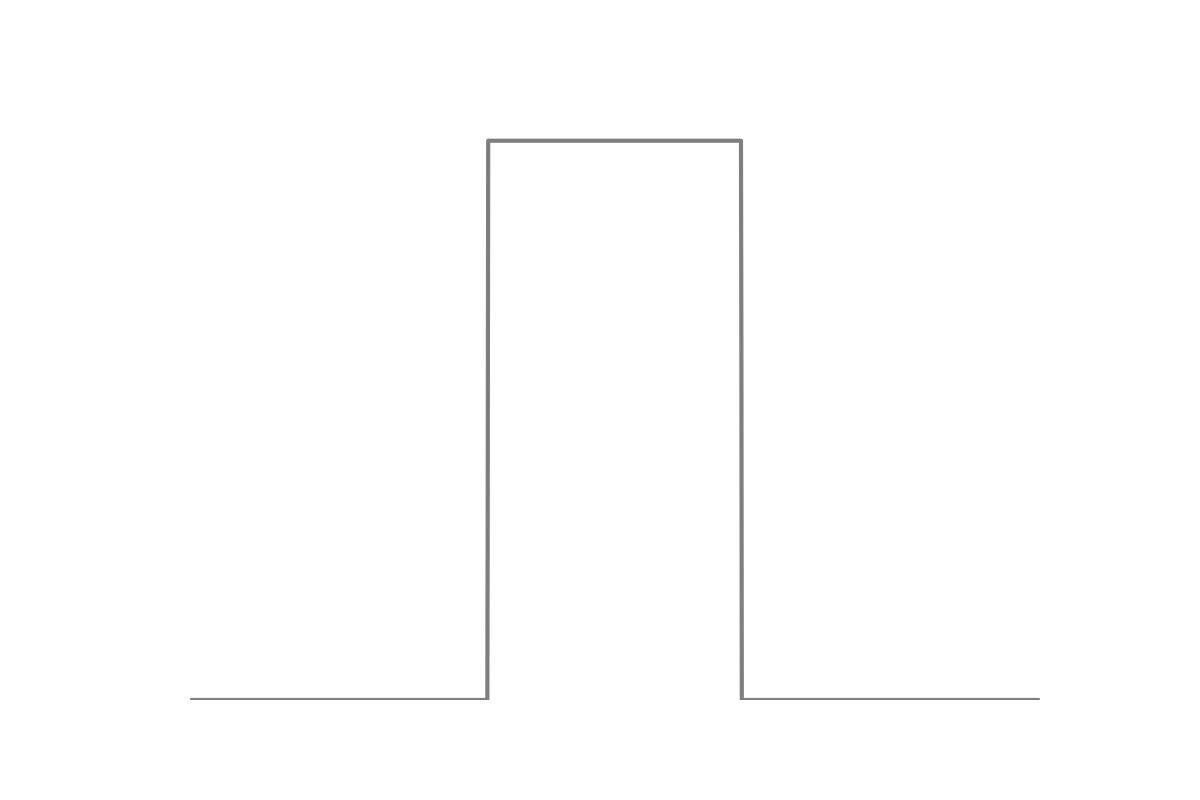
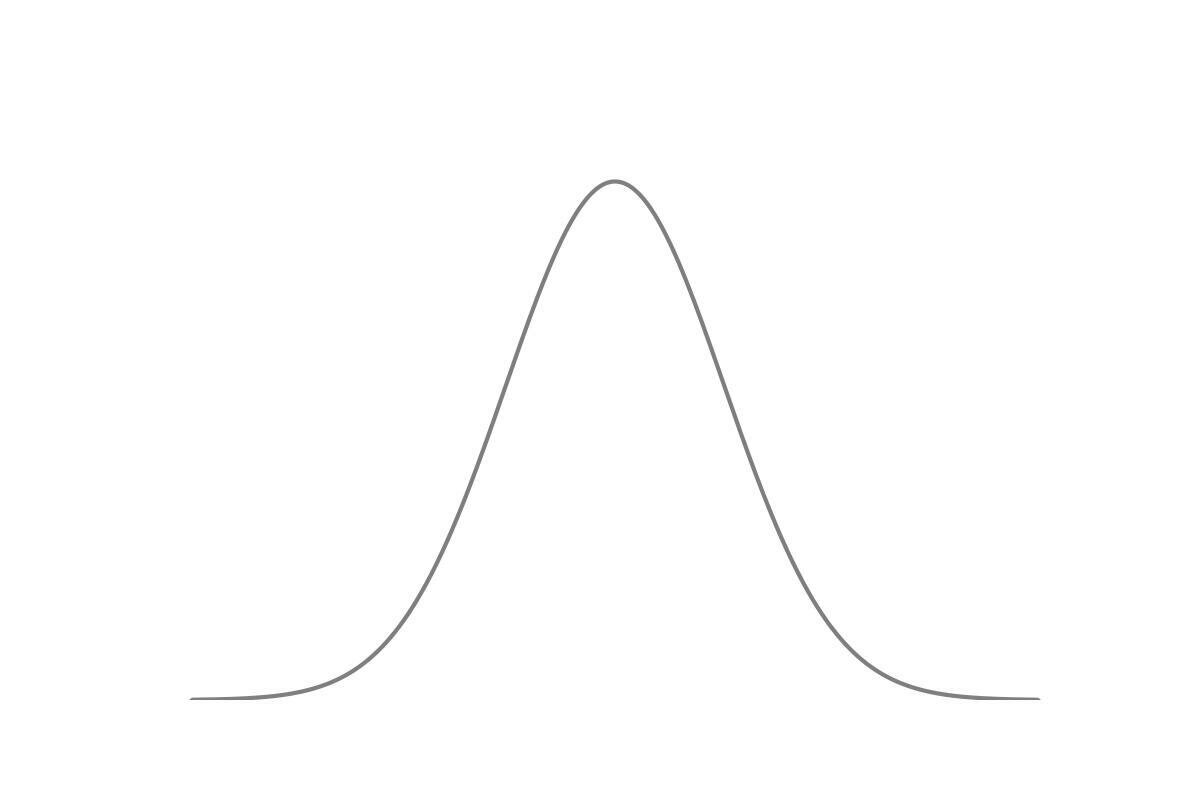
  • Equilibrium
g_t \underset{t \to \infty}{\to} M^{g_0}_{\textcolor{green}{0}}

expected behaviour

g_0

Maxwellian

distribution

  • Conservation of
  1. Mass
  2. Momentum
  3. Energy
\partial_t f_{t}(v) = Q_{\textcolor{purple}{\delta}}(f_{t})(v)

\(f \equiv f_{t}(v)\) density of fermions

the space-homogeneous

fermionic Boltzmann equation

  • Boltzmann-Fermi-Dirac equation

Pauli exclusion principle

0 \leq f_{t} \leq \frac{1}{\textcolor{purple}{\delta}}
0 < \textcolor{purple}{\delta} \ll 1
Q_{\color{purple} \delta}(f)(v) = \iint_{\R^3 \times \mathbb{S}^2} \left[f' f'_* (1- \textcolor{purple}{\delta} f)(1- \textcolor{purple}{\delta} f_*) - f f_* (1 - \textcolor{purple}{\delta} f')(1-\textcolor{purple}{\delta} f'_*) \right] B \; \mathrm{d} v_* \, \mathrm{d} \sigma
  • Collision operator
\frac{1}{\textcolor{purple}{\delta}}
v
\frac{1}{\textcolor{purple}{\delta}}
v
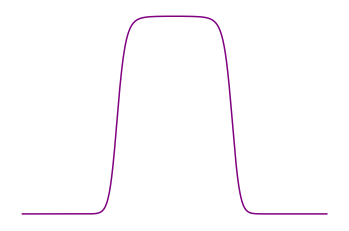
  • Equilibrium

Fermi-Dirac 

statistics

\frac{1}{\textcolor{purple}{\delta}}
v
  • Conservation of
  1. Mass
  2. Momentum
  3. Energy

- Existence & stability of solutions to homogeneous BFD for cut-off hard potentials

Lu, Wennberg

2001 -> 2008

Existence and uniqueness of solutions to inhomogeneous BFD for cut-off kernels

Dolbeault

1994

- Relaxation to equilibrium  of such solutions:

                             either \(f_0 =\)                      or    \(f_t \; \underset{t \to \infty}{\rightarrow}\)

Derivation of the equation from particles system (partially formal)

Benedetto, Castella, Esposito, Pulvirenti

2003

at which rate?

saturated state

Fermi-Dirac equilibrium

Some results on BFD

  The classical and fermionic Boltzmann equations

Trend to equilibrium

Introduction

 1. The entropy method

 2. Overview for kinetic equations

 3. Transfer from classical to fermionic

\partial_t f_t = Q(f_t)

\(D(h) \gtrsim {H(h|M^h)}^{1+\alpha}\)

\displaystyle \frac{\mathrm{d}}{\mathrm{d} t} H(f_t|M^{f_0}) =: - D(f_t)

\(D(h) \geqslant C H(h|M^h)\)

the entropy method

Relative entropy to equilibrium:

\(H(f_t|M^{f_0}) \lesssim t^{-1/\alpha}\)

\(H(f_t|M^{f_0}) \lesssim e^{-Ct} \)

Csiszár-Kullback-Pinsker

(for the Boltzmann entropy)

\|f_t - M^{f_0}\|_{L^1}^2 \lesssim H(f_t|M^{f_0})
H(g|M^g) = H(g) - H(M^g) \geq 0
  • Entropy (Lyapunov) functional \(H\)
  • Equilibrium distributions \(M\)

entropy dissipation

\forall h,

entropy inequality

  The classical and fermionic Boltzmann equations

Trend to equilibrium

Introduction

 1. The entropy method

 2. Overview for kinetic equations

 3. Transfer from classical to fermionic

fermionic entropy

classical entropy

H_{\textcolor{green}{0}}(g) = \int g \log g - g
H_{\textcolor{purple}{\delta}}(f) = \int f \log f + {\textcolor{purple}{\delta}}^{-1} (1 - {\textcolor{purple}{\delta}} f) \log (1-{\textcolor{purple}{\delta}} f)
M_{\textcolor{green}{0}}(v) = e^{a - b|v-u|^2}
\displaystyle M_{\textcolor{purple}{\delta}}(v) = \frac{e^{a - b|v-u|^2}}{1 + \textcolor{purple}{\delta} e^{a - b|v-u|^2}}

Equilibrium: Fermi-Dirac statistics

Equilibrium: Maxwellian

entropies and equilibria

classical Boltzmann

Fermionic boltzmann

H_{\textcolor{green}{0}}(g) = \int \Phi_{\textcolor{green}{0}}(g)
H_{\textcolor{purple}{\delta}}(f) = \int \Phi_{\textcolor{purple}{\delta}}(f)
M_{\textcolor{green}{0}}(v) = (\Phi_{\textcolor{green}{0}}')^{-1} \left(\alpha + \beta \cdot v + \gamma |v|^2 \right)
\displaystyle M_{\textcolor{purple}{\delta}}(v) = (\Phi_{\textcolor{purple}{\delta}}')^{-1} \left(\alpha + \beta \cdot v + \gamma |v|^2 \right)

Equilibrium: Fermi-Dirac statistics

Equilibrium: Maxwellian

entropies and equilibria

\Phi_{\textcolor{purple}{\delta}}'(x) = \log \left(\frac{x}{1 - \textcolor{purple}{\delta} x} \right)
\Phi_{\textcolor{green}{0}}' = \log

entropy    \(\displaystyle H : h \mapsto \int \Phi(h)\)          \(\Phi\)    \(\mathcal{C}^2\) st. convex

equilibrium 

M = (\Phi')^{-1} (\alpha \, \text{mass} + \beta \cdot \text{momentum} + \gamma \, \text{energy})

fermionic entropy

classical entropy

classical Boltzmann

Fermionic boltzmann

D_{\textcolor{green}{0}}(g) \gtrsim H_{\textcolor{green}{0}}(g|M_{\textcolor{green}{0}}^g)^{1 \textcolor{grey}{+ \alpha}}

Boltzmann

Carlen, Carvalho, Desvillettes, Toscani, Villani

1992 \(\to\) 2003

Landau

D_{\text{Landau}, \, \textcolor{purple}{\delta}}(f) \gtrsim H_{\textcolor{purple}{\delta}}(f |M_{\textcolor{purple}{\delta}}^f)^{1 \textcolor{grey}{+ \alpha}}

LAndau

Desvillettes, Villani

2000

Alonso, Bagland, Desvillettes, Lods

2020-2021

D_{\textcolor{purple}{\delta}}(f) \gtrsim H_{\textcolor{purple}{\delta}}(f|M_{\textcolor{purple}{\delta}}^f)^{1 \textcolor{grey}{+ \alpha}}

Boltzmann

Overview of entropy inequalities for kinetic equations

Fokker-Planck

log-Sobolev inequality

Fokker-Planck

D_{\text{Landau}, \, \textcolor{green}{0}}(g) \gtrsim H_{\textcolor{green}{0}}(g|M_{\textcolor{green}{0}}^g)^{1 + \textcolor{grey}{\alpha}}
D_{\text{FP}, \, \textcolor{green}{0}}(g) \gtrsim H_{\textcolor{green}{0}}(g|M_{\textcolor{green}{0}}^g)
D_{\text{FP}, \, \textcolor{purple}{\delta}}(g) \gtrsim H_{\textcolor{purple}{\delta}}(g|M_{\textcolor{purple}{\delta}}^g)

generalized

Gross

1975

Carillo, Laurençot, Rosado

2009

D_{FP, \, \textcolor{green}{0}}(g) = \int |\nabla \sqrt{g}|^2
H_{\textcolor{green}{0}}(g) = \int g \log g - g

classical

classical

classical

fermionic

fermionic

fermionic

H_{\textcolor{purple}{\delta}}(f) = \int f \log f + \textcolor{purple}{\delta}^{-1} (1- \textcolor{purple}{\delta} f) \log (1 - \textcolor{purple}{\delta} f)

Toscani \(\leqslant\) 1999,...

Transfer from classical to fermionic

B. 2024

  The classical and fermionic Boltzmann equations

Trend to equilibrium

Introduction

 1. The entropy method

 2. Overview for kinetic equations

 3. Transfer from classical to fermionic

transfer of inequalities

D_{\textcolor{green}{0}}(g) \gtrsim H_{\textcolor{green}{0}}(g|M_{\textcolor{green}{0}}^g)^{1 + \alpha}

We know:

\gtrsim \; \; D_{\textcolor{green}{0}}\left(\frac{f}{1 - \textcolor{purple}{\delta} f}\right)

entropy inequality for classical Boltzmann

\gtrsim \; \; H_{\textcolor{green}{0}} \left(\frac{f}{1- \textcolor{purple}{\delta} f} \left| M_{\textcolor{green}{0}}^{\frac{f}{1- \textcolor{purple}{\delta} f}} \right. \right)^{1 + \alpha}

entropy inequality for fermionic Boltzmann

We want:

D_{\textcolor{purple}{\delta}}(f) \gtrsim D_{\textcolor{green}{0}}\left(\frac{f}{1 - \textcolor{purple}{\delta} f}\right)

fermionic entropy dissipation of \(f\)

classical entropy dissipation of \( \displaystyle \frac{f}{1-\textcolor{purple}{\delta} f} \)

\( \gtrsim\)

D_{\textcolor{purple}{\delta}}(f) \textcolor{red} \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \quad \textcolor{orange}{\gtrsim} \;H_{\textcolor{purple}{\delta}}(f|M_{\textcolor{purple}{\delta}}^f)^{1 + \alpha}

?

\forall g,
\forall f,
\forall f,
H_{\textcolor{green}{0}}\left(\left.\frac{f}{1 - \textcolor{purple}{\delta} f}\right|M^{\frac{f}{1 - \textcolor{purple}{\delta} f}}_{\textcolor{green}{0}}\right) \geqslant H_{\textcolor{purple}{\delta}}(f|M^f_{\textcolor{purple}{\delta}}).

As soon as all terms make sense,

classical relative entropy to equilibrium of  \(\displaystyle \frac{f}{1-\textcolor{purple}{\delta} f}\)

fermionic relative entropy to equilibrium of \(f\)

Theorem.

comparison of relative entropies

B. 2024

R_g : \delta \in \R_+ \mapsto H_{\delta}\left( \frac{g}{1 + \delta g} \left|M^{\frac{g}{1 + \delta g}}_{\delta} \right. \right)

Fix

is nonincreasing on \(\R_+\).

g \geqslant 0,
  • nice representation of the relative entropy to equilibrium
  • general link between entropy and equilibrium
  • fact that \(x \mapsto -\left(\frac{x}{1+\delta x} \right)^2\) is decreasing

Show that \(R_g' \leq 0\) on \(\R_+^*\) and \(R_g\) continuous on \(\R_+ \)

Proof  scheme

We show:

We use:

Proposition.

0\leqslant f \in L^1_2(\R^3)
\displaystyle \textcolor{black}{ 1 - \textcolor{purple}{\delta} f \geqslant} \kappa,

For all

such that

\textcolor{purple}{\delta} \textcolor{black}{> 0,} \;\; \kappa \textcolor{black}{\in (0,1)}

and

Classical / Fermi-Dirac equivalence

\textcolor{black}{H_{\textcolor{purple}{\delta}}(f|M^f_{\textcolor{purple}{\delta}}) \leqslant H_{\textcolor{green}{0}}\left(\left.\frac{f}{1 - \textcolor{purple}{\delta} f}\right|M^{\frac{f}{1 - \textcolor{purple}{\delta} f}}_{\textcolor{green}{0}}\right) \leqslant} \textcolor{black}{e}^{ \textcolor{black}{16} \, { \textcolor{black}{(}\kappa^{\textcolor{black}{-1}} \textcolor{black}{- 1)} } } \textcolor{black}{\; H_{\textcolor{purple}{\delta}}(f|M^f_{\textcolor{purple}{\delta}})} \phantom{\frac{1-\kappa}{\kappa}}
\textcolor{black}{D_{\textcolor{purple}{\delta}}(f) \leqslant D_{\textcolor{green}{0}}\left(\frac{f}{1 - \textcolor{purple}{\delta} f}\right) \leqslant} \kappa^{\textcolor{black}{-4}} \textcolor{black}{ \; D_{\textcolor{purple}{\delta}}(f)}

For Boltzmann/BFD (& Landau/LFD) dissipations:

entropy inequality for Boltzmann

entropy inequality for Boltzmann-Fermi-Dirac

\kappa
\iff
1
\textcolor{purple}{\delta} f
\kappa
D_{\textcolor{purple}{\delta}}(f) \gtrsim H_{\textcolor{purple}{\delta}}(f|M^f_{\textcolor{purple}{\delta}}), \; \; \forall f \in \mathcal{F}
\forall g \in \mathcal{G}, \; \; D_{\textcolor{green}{0}}\left(g\right) \gtrsim H_{\textcolor{green}{0}}\left(\left.g\right|M^{g}_{\textcolor{green}{0}}\right)

Conclusion

2024

Conclusion

Conclusion

  • Entropy inequality \(\implies\) rate of convergence to equilibrium
  • Known entropy inequalities for classical Boltzmann
  • Transfer:  classical entropy inequality \(\implies\) fermionic entropy inequality
  • Result: large range of fermionic entropy inequalities
  • Implication: explicit rate of convergence to equilibrium for fermionic Botzmann, by Lods & B. (hard potentials) and Jiang et Wang (moderately soft potentials)
D \gtrsim H^{1 + \alpha}
\|f_t - M\| \lesssim t^{-\alpha}

contribution

method

literature

Thank you for your attention!

General weighted \(L^p\) Csiszár-Kullback-Pinsker

\|f-M^f\|^2_{L^p_{\varpi}} \leqslant {\small C_{\Phi, \varpi, p, f, M^f}} \; H(f|M^f),

Proposition.

(general entropy)

\(\displaystyle H(f) = \int\Phi(f)\),   \(\Phi \; \; \mathcal{C}^2\) st. convex,   \(M^f\) equilibrium, and

C_{\Phi, \varpi, p,f,M^f} = \left(\int_0^1 (1-\tau) \left\| \Phi''((1-\tau)M^f + \tau f)^{-1} \right\|_{L^{\frac{p}{2-p}}_{\varpi^2}}^{-1} \, \mathrm{d} \tau \right)^{-1}

For any \(f\), any \(p \in [1,2]\) and \(\varpi\) weight,

\|f-M_0^f\|^2_{L^p_{\varpi}} \leqslant 2 \max \left(\|f\|_{L^{\frac{p}{2-p}}_{\varpi^2}}, \|M_0^f\|_{L^{\frac{p}{2-p}}_{\varpi^2}} \right)\, H_{0}(f|M_0^f),

Corollary.

For any \(0\leq f \in L^1_2\cap L \log L(\R^3)\), \(p \in [1,2]\) and \(\varpi : \R^3 \to \R_+\),

(Boltzmann entropy)

\(\displaystyle H_0\) Boltzmann entropy and \(M_0^f\) Maxwellian.

[simplified]