Quasi-resonant collisions in kinetic theory and bi-temperature systems
38e séminaire de mécanique des fluides numérique
CEA-SMAI/GAMNI
IHP, January 27, 2026
\(\phantom{x}^*\)post-doc at CERMICS, École des Nationale des Ponts et Chaussées
a peculiar polyatomic Boltzmann model
Microscopic
Macroscopic


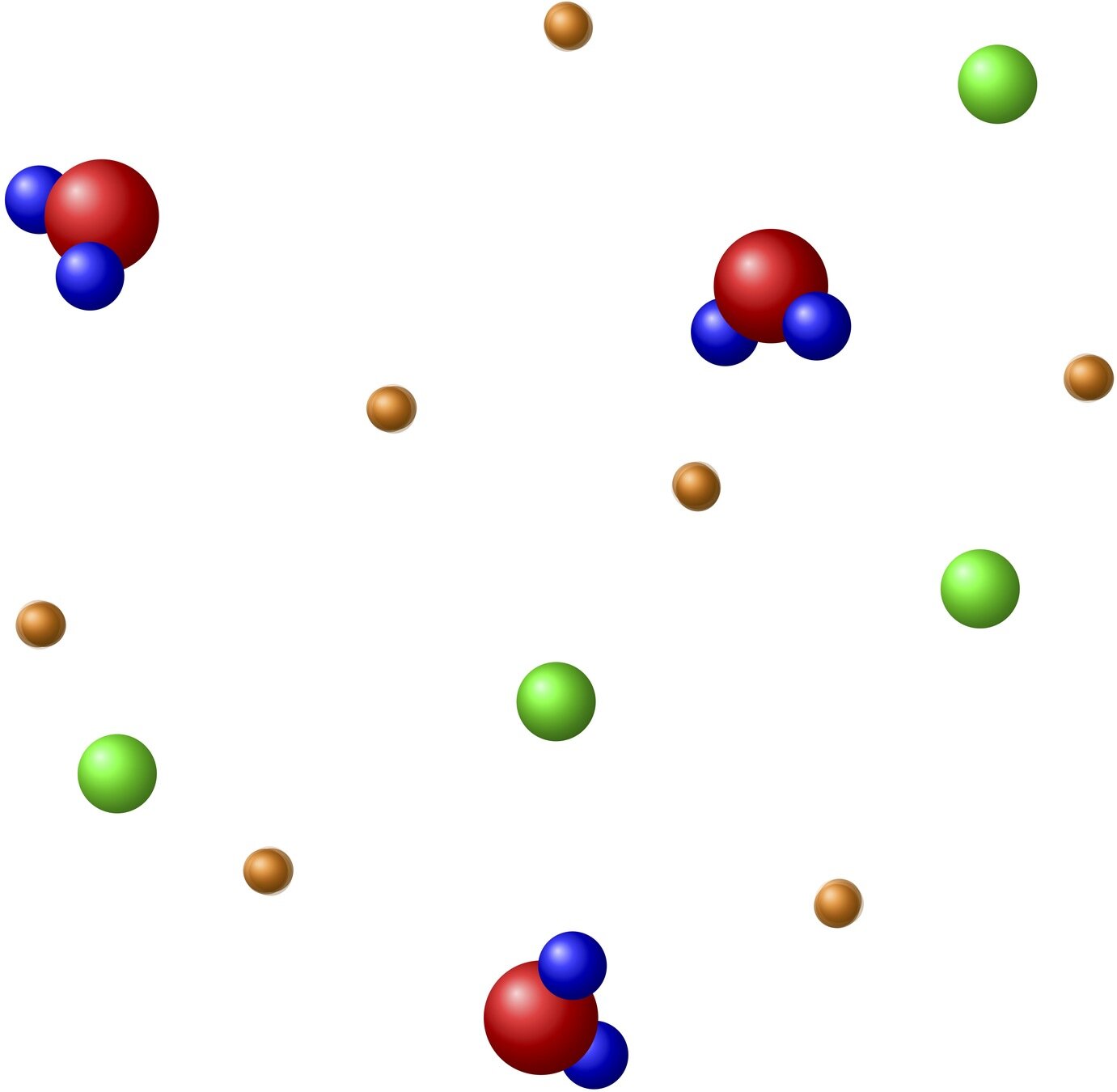
Kinetic theory: statistical description of gases
Mesoscopic
gaz large collection of molecules
Part 1. Standard polyatomic Boltzmann
Part 2. Polyatomic Boltzmann with quasi-resonant collisions
Outline
- How to model quasi-resonance
- Peculiar characteristic of the dynamic
- Numerical experiments
Part 1. Standard polyatomic Boltzmann

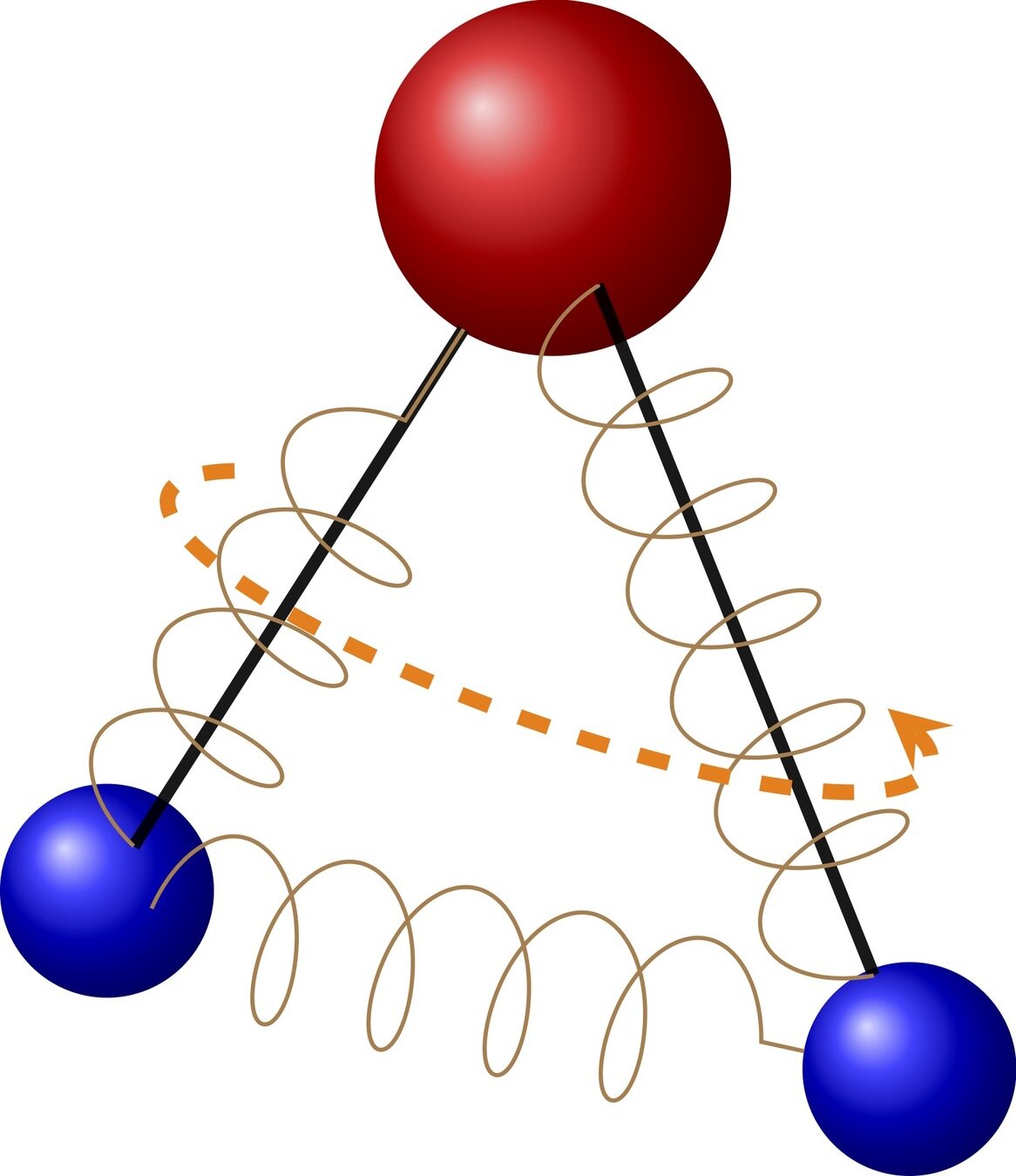
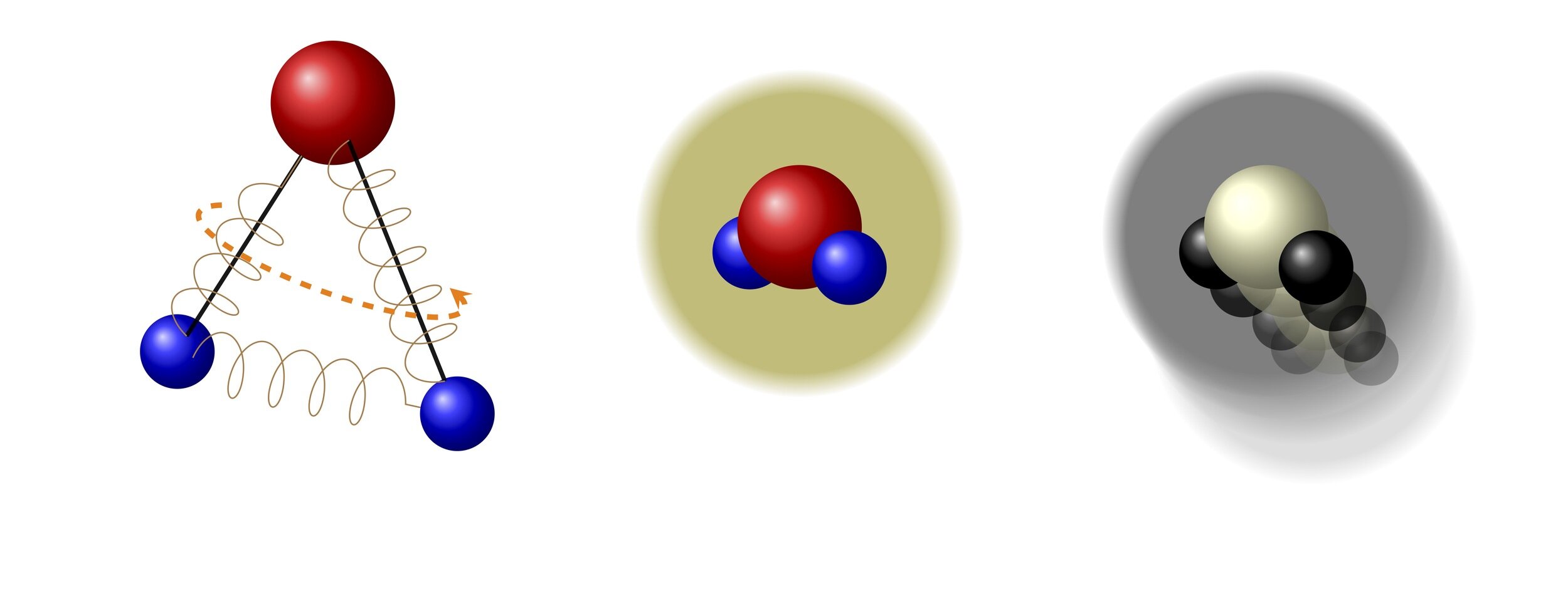
polyatomic molecules have an internal structure
position, velocity
position, velocity, angular velocity, vibration modes,...
monoatomic
polyatomic
Internal state
Internal
energy quantile
Internal
energy level
How to describe the internal structure?
[Borgnakke\(\text{--}\)Larsen 75', Desvillettes 97']
[Wang-Chang\(\text{--}\)Uhlenbeck 51', Waldmann 57', Snider 60']
[Taxman 58', B.\(\text{--}\)Bisi\(\text{--}\)Groppi '23]


- We study \(f \equiv f_{t,x}(v, I)\) density of molecules
the polyatomic Boltzmann equation
(with internal energy levels description)
Boltzmann equation:

energy of the molecule
- Description of a gaz as a collection of molecules
Each molecule either moves in straight line of collides with another molecule
- We study \(f \equiv f_{t}(v, I)\) density of molecules
the space homogeneous
polyatomic Boltzmann equation
(with internal energy levels description)
Space homogeneous Boltzmann equation

energy of the molecule
- Assume that the gaz is homogeneous in space
Dynamic driven by collisions between molecules
the collision operator \(Q\)

Conservation laws

(momentum)
(total energy)
energy of the molecule
\(\textcolor{purple}{B(v,v_*,v',v'_*,I,I_*, I',I'_*)} > 0 \iff \) the collision is possible
Collision kernel
Entropy and equilibrium
Boltzmann entropy functional
Boltzmann's H-theorem
(i) 2\(^{nd}\) principle of thermodynamics
(ii) Equilibrium
If
then
entropy dissipation functional
For any
With \(\mathcal{M}\) the Maxwellian (Gibbs) distribution
\(\textcolor{blue}{\rho}\) average density
\(\textcolor{blue}{u}\) bulk velocity
\(\textcolor{blue}{T}\) temperature
Part 2. Polyatomic Boltzmann with quasi-resonant collisions
quasi-resonant collisions

(separation kinetic/internal)
Observed experimentally, e.g. \(\mathrm{CO}_2\)

quasi-resonant possible collisions
How to make it rigorous?
(almost separation kinetic/internal)
resonant possible collisions
standard possible collisions
Part 2. Polyatomic Boltzmann with quasi-resonant collisions
How to model quasi-resonance?
Other contributions :
- Aoki-Bernhoff (2025)
- Graille-Magin-Massot (2012)
- Frozen collisions of Torrilhon and Pavic
quasi-resonant collisions by truncation of the kernel
Set of possible collisions \(\equiv\) support of the collision kernel
resonant possible collisions

Let
a standard collision kernel
standard possible collisions
quasi-resonant collisions by truncation of the kernel
Set of possible collisions \(\equiv\) support of the collision kernel
quasi-resonant possible collisions

Let
a standard collision kernel
\(\mathcal{V}_{\varepsilon}\)
Family of collision kernels:
truncation family
the truncation family
a standard collision kernel
\(\mathcal{V}_{\varepsilon}\)
The collision is in \(\textcolor{red}{\mathcal{V}_{\varepsilon}}\) if
- Pre-and post-collision energy ratios:
- A diffeomorphism \(\eta : (0,1) \to \R\)
Remark:
the collision is resonant
The collision is in \(\textcolor{green}{\mathcal{V}_{0}}\) iff
\(\mathcal{V}_{0}\)
pre-collision kinetic energy
total energy
post-collision kinetic energy
total energy
the truncation family
\(\mathcal{V}_{\varepsilon}\)
The collision is in \(\textcolor{red}{\mathcal{V}_{\varepsilon}}\) if
- Pre-and post-collision energy ratios:
pre-collision kinetic energy
total energy
- Take \(\eta : R \in (0,1) \mapsto \log \frac{R}{1-R}\)
In practice:
controls a ratio of ratios of ratios!
a standard collision kernel
Remark:
the collision is resonant
The collision is in \(\textcolor{green}{\mathcal{V}_{0}}\) iff
post-collision kinetic energy
total energy
Family of collision kernels:
Family of collision operators:
The quasi-resonant Boltzmann dynamics
Family of quasi-resonant Boltzmann dynamics
RESONANT ASYMPTOTICS \(\varepsilon \to 0\)
Resonant asymptotics
we expect the quasi-resonant dynamic to be "close" to the resonant one
Part 2. Polyatomic Boltzmann with quasi-resonant collisions
Peculiar characteristic of the dynamic
Resonant and Quasi-resonant long-time properties
and consequent expected behaviour
Equilibrium:
two distinct temperatures
kinetic
temperature
internal
temperature
Equilibrium:
two distinct temperatures
same
temperature
one single temperature
For the resonant dynamic
For the quasi-resonant dynamic
Boudin-Rossi-Salvarani 2022
time
\(\mathcal{O}(1)\) short time
\(\mathcal{O}(\textcolor{red}{\varepsilon}^{-2})\) long time
relaxation towards a
two-temperature
Maxwellian
- the solution (almost) remains of two-temperature Mawellian shape
- the kinetic (\(\textcolor{blue}{T_k}\)) and internal (\(\textcolor{blue}{T_i}\)) temperatures relax towards each other
(1)
(2)
Expected behaviour of the quasi-resonant dynamics 1/2
If \(\varepsilon \ll 1\), we expect
Explicit ODE system on the two temperatures?
Explicit Landau-Teller ODE system
Proposition.
If
with
then for a certain family of kernels \(B^{\textcolor{grey}{std}}\) and energy laws \(\varphi\), we have
with \(\alpha\) explicit.
Internal temperature at time \(t\):
(2)
Long-time behaviour: Landau-Teller relaxation of (\(\textcolor{blue}{T_k}\)) and (\(\textcolor{blue}{T_i}\)) towards each other
expected behaviour of the QUASI-RESONANT dynamics 2/2
let's check this numerically!
time
\(\mathcal{O}(1)\) short time
\(\mathcal{O}(\textcolor{red}{\varepsilon}^{-2})\) long time
relaxation towards a
two-temperature
Maxwellian
- the solution (almost) remains of two-temperature Mawellian shape
- the kinetic (\(\textcolor{blue}{T_k}\)) and internal (\(\textcolor{blue}{T_i}\)) temperatures relax towards each other
(1)
(2)
Part 2. Polyatomic Boltzmann with quasi-resonant collisions
Numerical experiment
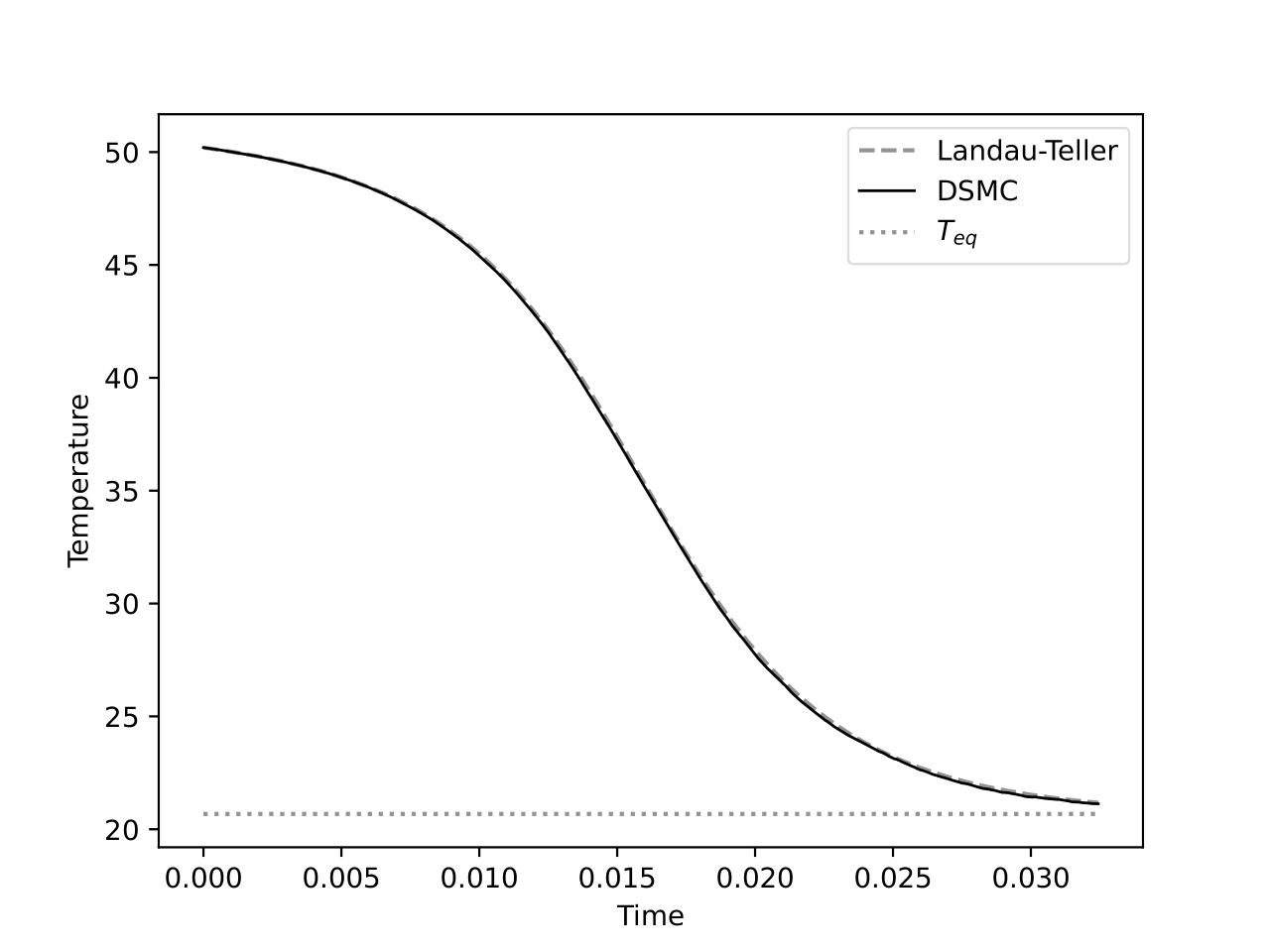
Numerical experiment
Parameters
- Simulation of the quasi-resonant Boltzmann equation with DSMC
- Integration of the LT ODE system
Numerical experiment
Goal. Check if
temperatures associated with the quasi-resonant Boltzmann dynamics
temperatures of the Landau-Teller ODE system
Simulation of the quasi-resonant Boltzmann equation with DSMC
- \(N\) numerical particles, each with velocity \(v\) and energy quantile \(q\)
- at each time step, randomly select couples of particles to collide, according to the collision kernel
- for each collision, randomly draw the new states of the particles, according to the collision kernel
Conclusion
- The shape of the distribution is known at all times (two-temperature Maxwellian)
For the quasi-resonant Boltzmann dynamic
- The two temperatures are related to a Landau-Teller ODE system
- This ODE system is explicit from the Boltzmann model in some cases
Thank you for your attention!