Approaches for modeling polyatomic molecules in kinetic theory
University of Novi Sad
April 15, 2025
\(\phantom{x}^*\)CERMICS, École des Ponts, France



Microscopic
Macroscopic


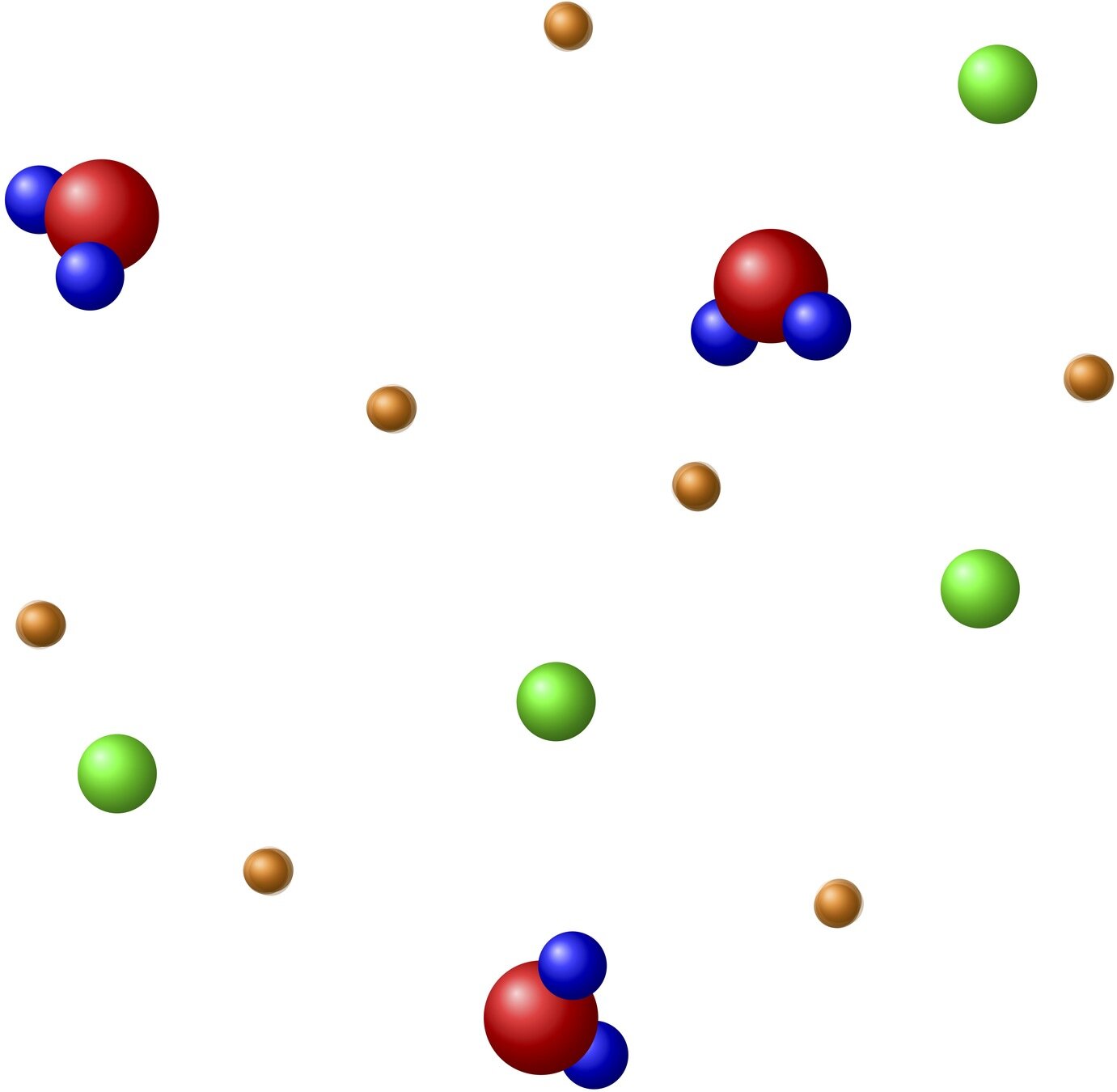
Kinetic theory: statistical description of gases
Mesoscopic
Polyatomic molecules: with internal structure

Monoatomic :
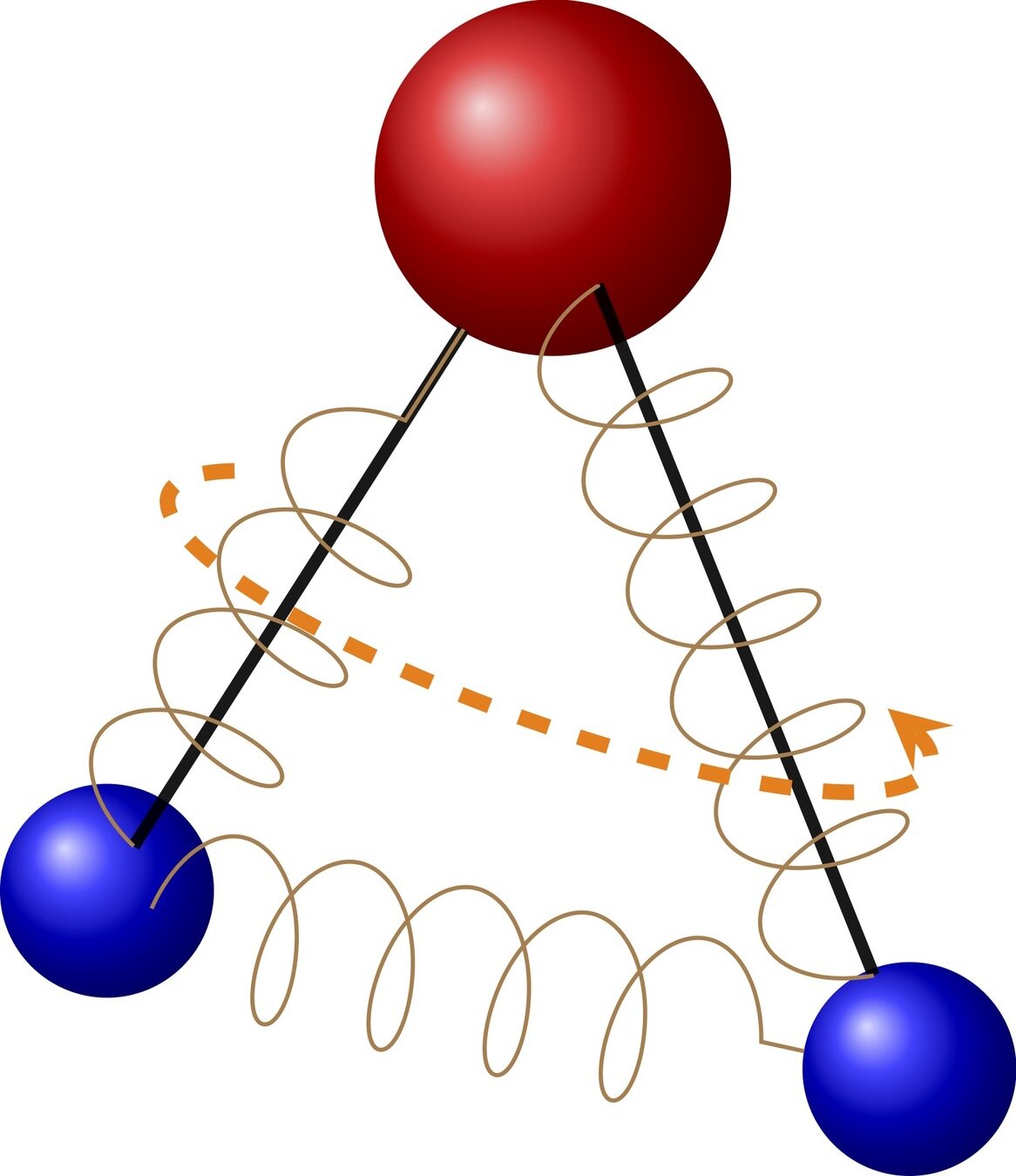
Polyatomic :
Outline
- The Boltzmann equation for monoatomic gases
- Extension to polyatomic gases
- Three points of view for modeling a polyatomic molecule


The original Boltzmann equation

[A. Greg: Kinetic theory of gases, wikipedia.]
advection
collisions

Density of molecules
\(f \equiv f_{t}(x,v)\)

(monoatomic)
the collision operator

Conservations
\(B(v,v_*,\sigma)\) : nature of interaction
hard spheres
\(B(v,v_*,\sigma) = |v-v_*|\)
power law potential
\(B(v,v_*,\sigma) = b(\cos \theta)|v-v_*|^\gamma\)
...
[A. Greg: Kinetic theory of gases, wikipedia.]
the Homogeneous Boltzmann equation
Density of molecules: \(f_t(v)\)

\(x \)
advection
\(+ \, v \cdot \nabla_x f\)
















Entropy and equilibrium
The Boltzmann entropy:
2. \(D(g) = 0 \iff g =M \) a Maxwellian:
characterization of equilibria
Boltzmann's H Theorem
1. If \(f \equiv f_t(v)\) solves
\(2^{nd}\) principle of thermodynamics
\((HB)\)
then
Illustration of the expected behaviour
Degrees of freedom and heat capacity
Microscopic energy of \(f\):
with
At equilibrium, \(f = M\):
- Number of degrees of freedom \(:=\)
- Heat capacity at constant volume \(:=\)
monoatomic gas
- The Boltzmann equation for monoatomic gases
- Extension to polyatomic gases
- Three points of view for modeling a polyatomic molecule




polyatomic molecules have an internal structure
continuous
[Borgnakke\(\text{--}\)Larsen 75', Desvillettes 97']
discrete
[Wang-Chang\(\text{--}\)Uhlenbeck 51', Waldmann 57', Snider 60']

Density of molecules \(f \equiv f(t,x,v)\)
Density of molecules \(f \equiv f(t,x,v,\textcolor{orange}{?})\)
Internal state
Internal
energy quantile
Internal
energy level
[Taxman 58']
general mathematical framework
[Bisi\(\text{--}\)TB\(\text{--}\)Groppi '22]
[Gamba\(\text{--}\)Pavić-Čolić '20]
the two requirements for a polyatomic kinetic model
1. Modeling the molecule
2. Modeling the interaction between molecules
this presentation

Determine the collision kernel
\(B(v,v_*,\sigma,I,I_*,I',I'_*)\)
Monchick, Mason, Hellman...

\(f(t,x,v,\textcolor{orange}{?})\)

\(\R^3 \times \textcolor{orange}{\mathcal{E}}\)
general mathematical framework based on internal states
state of the molecule
space of states
energy of the molecule
\((\mathcal{E}, \mu)\)
\(\varepsilon : \mathcal{E} \to \R\)
2. Internal energy function:
existence of fundamental energy level
finiteness of the partition function
\(\bar{\varepsilon} := \varepsilon - \inf_{\mu} {\varepsilon}\) (\( : \mathcal{E} \to \R_+\))
\(\displaystyle Z(\beta) := \int_{\mathcal{E}} \exp(-\beta \, \bar{\varepsilon}(\zeta)) \, \mathrm{d} \mu(\zeta) < \infty\), \(\forall \, \beta >0\).
1. Space of internal states:
Assumptions
measured space
Ingredients
\(\sigma\)-finiteness of \(\mu\)
measurable function
\(f \equiv f_{t,x}(v, \textcolor{orange}{\zeta})\) density of molecules

the polyatomic Boltzmann equation
1. internal states
Boltzmann equation:
Collision operator:

Conservation of
mass, momentum, energy :
\(f \equiv f_{t,x}(v, \textcolor{olive}{I})\) density of molecules
the polyatomic Boltzmann equation
2. (continuous) internal energy levels
Boltzmann equation:
Collision operator:

Conservation of
mass, momentum, energy :

energy law
[Borgnakke\(\text{--}\)Larsen 75', Desvillettes 97']
Entropy and equilibrium in the polyatomic case
The Boltzmann entropy:
2. \(D(g) = 0 \iff g =M \) is a generalized Maxwellian:
characterization of equilibria
Boltzmann's H Theorem
1. If \(f \equiv f_t(v,\textcolor{orange}{\zeta})\) solves
\(2^{nd}\) principle of thermodynamics
then
Degrees of freedom and heat capacity
Microscopic energy of \(f\):
At equilibrium, \(f = M\):
- Number of degrees of freedom \(:=\)
- Heat capacity at constant volume \(:=\)
- The Boltzmann equation for monoatomic gases
- Extension to polyatomic gases
- Three points of view for modeling a polyatomic molecule



parallel with probability setting leading to 3 points of view

polyatomic internal structure
probability setting
\( (\Omega, \; \mathbb{P}) \) space of events
\( X : \Omega \to \R_+ \) random variable
\( (\mathcal{E}, \; \mu) \) space of internal states
\( \bar{\varepsilon} : \mathcal{E} \to \R_+ \) energy function
\( \bar{\varepsilon} = \varepsilon - \inf \varepsilon \)

\( (\R_+, \, \mathbb{P}_X)\) space of outcomes
\( \mathbb{P}_X\) on \(\R_+\) law of \(X\)
\( (\R_+, \, \mu_{\bar{\varepsilon}}) \) space of energy levels
\( \mu_{\bar{\varepsilon}}\) on \(\R_+\) energy law

\( ((0,1), \, Lebesgue) \) space of quantiles
\( F^{\leftarrow}_{\mathbb{P}_X}: (0,1) \to \R_+\) quantile function
\( ((0,\, q^{\max}), \, Lebesgue) \) space of energy quantiles
\( F^{\leftarrow}_{\mu_{\bar{\varepsilon}}}: (0,\, q^{\max}) \to \R_+\) energy quantile func.
\(q^{\max} := \mu(\mathcal{E})\)
\(\mathbb{P}_X = X \# \mathbb{P} \)
\(\mu_{\bar{\varepsilon}} = \bar{\varepsilon} \#\mu \)

internal state
internal energy level
internal energy quantile
Paradigms and a suggestion for their use
\(\zeta \in \mathcal{E}\)
\(\mu\)
\(\bar{\varepsilon}\)
\( I \in \R_+\)
\(\mu_{\bar{\varepsilon}}\)
\( q \in (0,q^{\max})\)
\(\mathrm{Id}_{\R_+}\)
\(F_{\mu_{\bar{\varepsilon}}}^{\leftarrow}\)
Lebesgue
variable
measure
energy function
Physical modeling
& general proofs
Computations
& technical proofs
Numerical simulations
(particle-based)


well-suited for
(grounded)



Internal states
Internal energy levels
Internal energy quantiles
State-based
Energy-based
2 approaches, 3 points of view - loss of information
contains all the information
contains only the information on the energy
loss of information
A typical example for the diatomic molecule
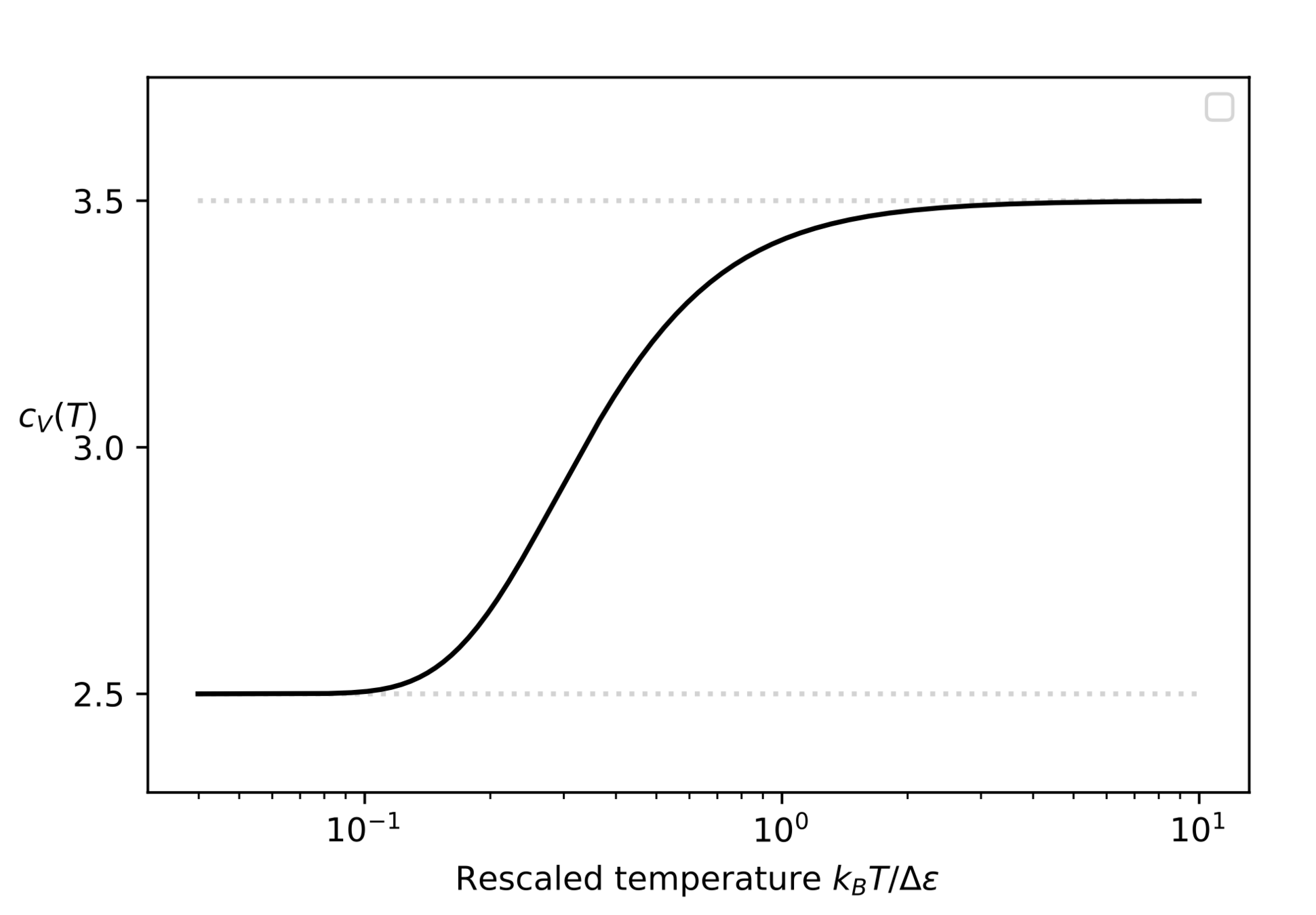
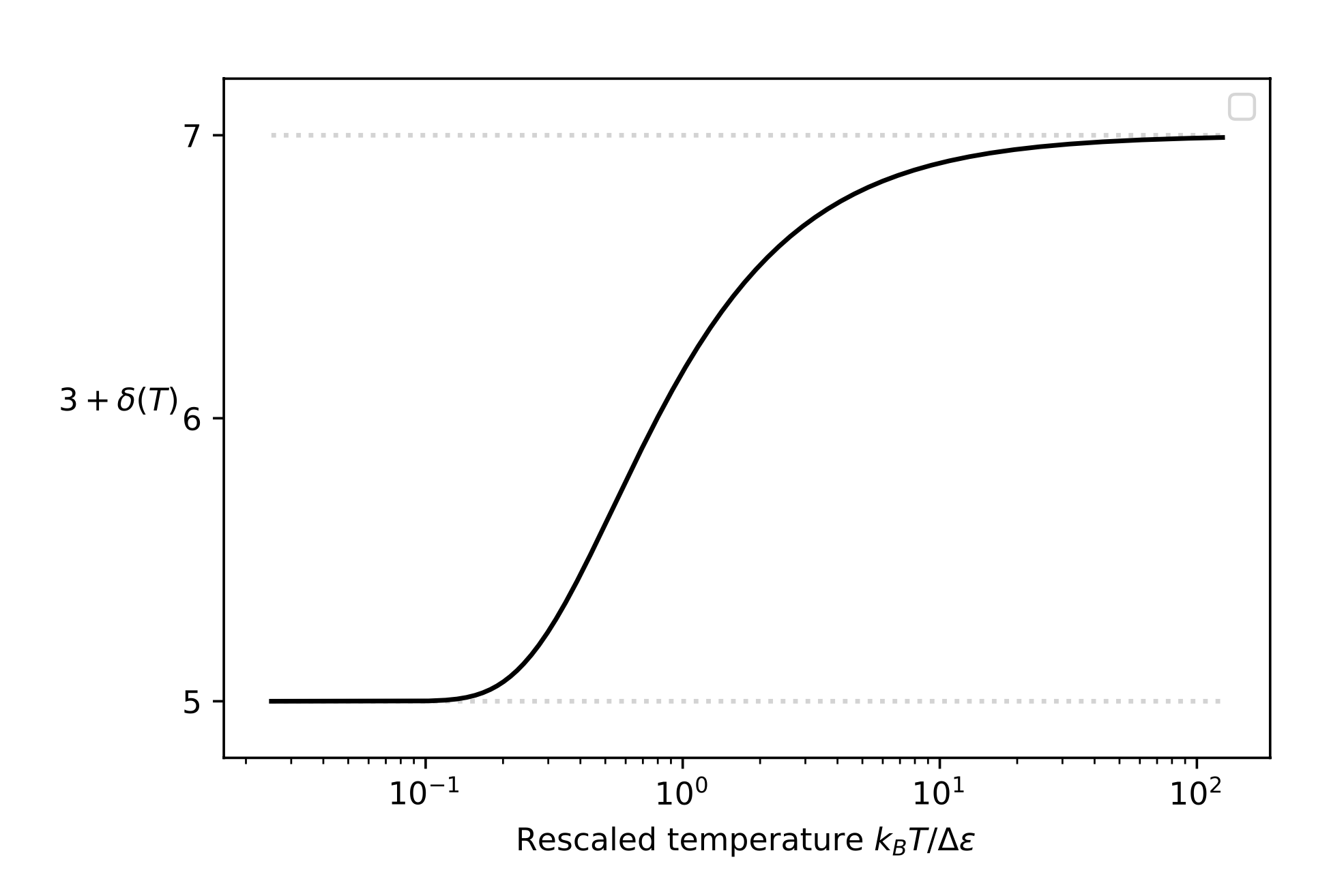
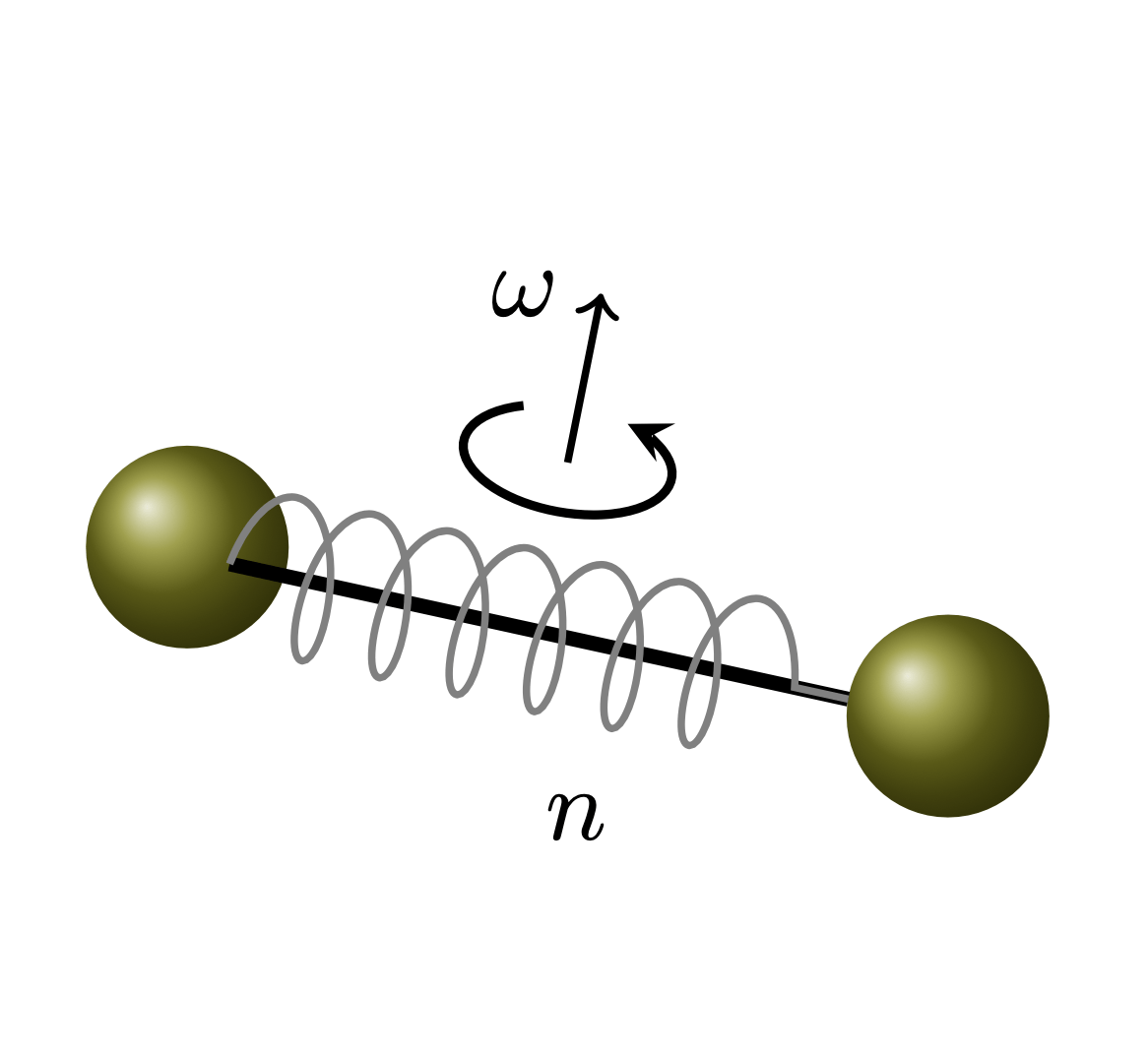
Physical model:
- Classical Rigid-Rotor for rotation
- Quantum harmonic oscillator for vibration
Number of degrees of freedom (T)
Heat capacity at constant volume (T)
internal
states
internal energy levels
internal energy quantiles
\(\mathcal{E} = \R^2 \times \N\)
\(\mu = Lebesgue_{\R^2} \otimes Counting_{\N}\)
\(\varepsilon (\omega,n) =\frac12 \mathcal{J} |\omega|^2 + \left( n + \frac12 \right) \Delta \epsilon\)
\( (\R_+,\varphi(I) dI) \)
\( \mathrm{Id}_{\R_+}\)
\( (0,+\infty) \)
\( Lebesgue_{\R^*_+} \)
\(\varphi(I) =\displaystyle \frac{2\pi}{\mathcal{J}} \left\lceil \frac{I}{\Delta \epsilon} \right\rceil \)
\(\displaystyle F^{\leftarrow}_{\mu_{\bar{\varepsilon}}}(q) = \Delta \epsilon \left(\frac{\hat{q}}{\ell(\hat{q})+1} + \frac{\ell(\hat{q})}{2} \right)\)
\(\displaystyle \hat{q} := \frac{\mathcal{J}}{2\pi \; \Delta \epsilon} \; q\), \( \displaystyle \ell(\hat{q}) := \left\lfloor \frac{4 \, \hat{q}}{\sqrt{1 + 8 \, \hat{q}} \, + 1} \right\rfloor\)
"non-polytropic"
polyatomic models in the literature (in practice)

\( (\R_+, \, \mu_{\bar{\varepsilon}}) \) space of energy levels
\( \mu_{\bar{\varepsilon}}\) on \(\R_+\) energy law
1. \(\mu_{\bar{\varepsilon}}\) is a discrete measure
supported on \(\{\epsilon_n\}_n\)
model with discrete energy levels
[Wang Chang-Uhlenbeck 51',
Bisi-Groppi-Spiga 2005...]
with energy levels \(\{\epsilon_n\}_n\)
2. \(\mu_{\bar{\varepsilon}}\) has a density \(\varphi\) w.r.t.
Lebesgue measure
model with continuous energy levels
[Borgnakke-Larsen 75',
Desvillettes 97'...]



States
Energy quantiles
Build
Analyse
Simulate


Energy levels
Thank you for your attention!