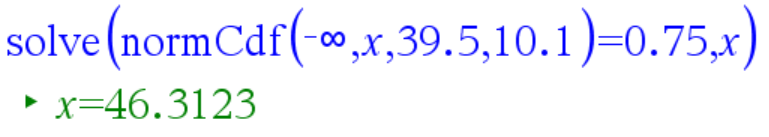Normaalijakauma
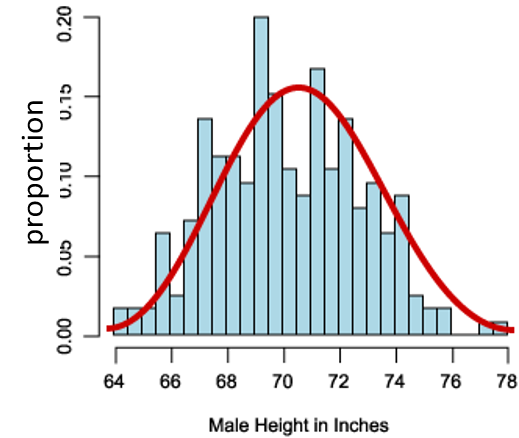
Monien jatkuvien tilastomuuttujien jakauma mukailee kirkonkellon muotoista käyrää
Tällaista jakaumaa kutsutaan normaalijakaumaksi
Normaalijakauman tiheysfunktio on
\(f(x) = \frac{1}{\sigma \sqrt{2\pi}}e^{-\frac{1}{2}(\frac{x-\mu}{\sigma})^2} \)
jossa \(\mu\) on odotusarvo ja \(\sigma\) keskihajonta

Normaalijakauman kertymäfunktiolle ei ole olemassa lauseketta, mutta sen arvoja voi kuitenkin laskea laskimella
Jos satunnaismuuttuja on normaalijakautunut odotusarvolla \(\mu\) ja keskihajonnalla \(\sigma\), merkitään \(X\sim N(\mu,\sigma)\)

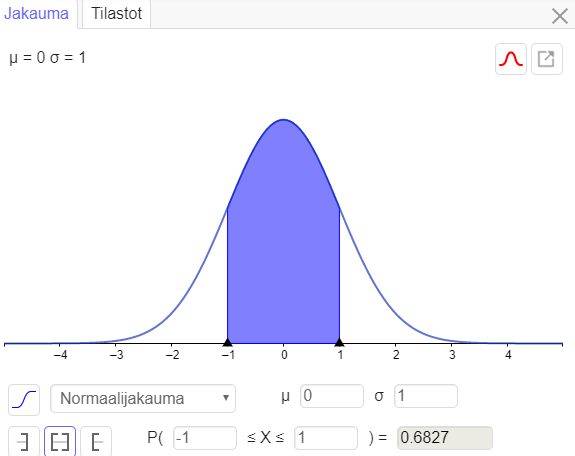
Esim: \(X\sim N(0,1)\), laske \(P(-1\leq X\leq 1)\)
Nspire:
Geogebra:
Urosmerisaukkojen painon keskiarvoksi punnittiin 39,5 kg ja keskihajonnaksi 10,1 kg. Arvioi, millä todennäköisyydellä satunnainen urosmerisaukko on alle 30 kg.
Merkitään painoa satunnaismuuttujalla \(X\) ja oletetaan, että \(X\sim N(39,5 , 10,1)\).
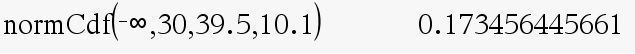
V: N. 17%
Lasketaan \(P(X<30)\)
Urosmerisaukkojen painon keskiarvoksi punnittiin 39,5 kg ja keskihajonnaksi 10,1 kg. Arvioi, kuinka painavia on urosmerisaukkojen muhkuin neljännes.
Merkitään painoa satunnaismuuttujalla \(X\) ja oletetaan, että \(X\sim N(39,5 , 10,1)\).
Pitäisi ratkaista \(a\) yhtälöstä \(P(X\geq a)=0.25\) tai \(P(X\leq a)=0.75\)

Geogebrassa voi kirjoittaa suoraan todennäköisyyden, jolloin Geogebra laskee ylä/alarajan:
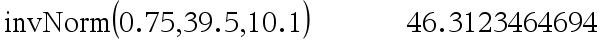
Nspiressä ratkaistaan yhtälö tai valitaan "Normaali käänteinen"
V: Yli 46,3 kg