Keskiarvon keskivirhe ja luottamusvälin laskeminen
- Mikko keräsi 500 omenaa, tsemppasi ja punnitsi kaikki omenat. Keskipainoksi saatiin 159 g ja keskihajonnaksi 12 g
- Mikko kuitenkin mietti, kuinka lähelle hän olisi päässyt, jos olisi punninnut vain 30 omenaa. Kun hän valitsi 30 satunnaista omenan hän sai näiden keskipainoksi 162 g.
- Mikko rupeaa pohtimaan, mitä tapahtuisi, jos hän valitsisi uudestaan satunnaisesti 30 omenaa, ja laskisi näiden keskiarvon. Tällöin hän saisi luultavasti jonkin hieman äskeisestä poikkeavan keskipainon.
- Jos näin tehtäisiin tarpeeksi monta kertaa, saataisiin hahmoteltua näin laskettujen keskiarvojen jakauma
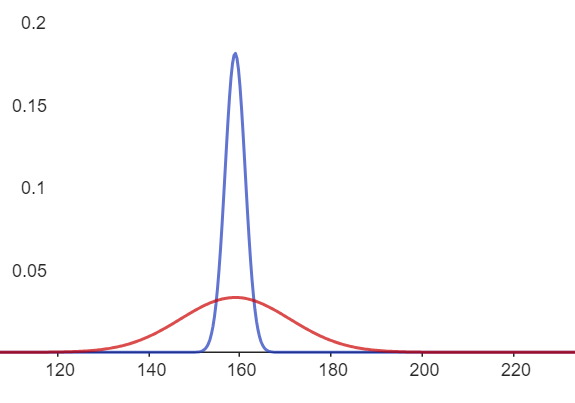
Jos satunnaisesti valitun omenan paino on normaalijakautunut*, silloin myös 30 satunnaisesti valitun omenan painojen keskiarvo on normaalijakautunut! Näiden odotusarvot ovat samat, mutta keskiarvon jakauman keskihajonta on keskiarvon keskivirhe \(s_{\bar{x}}=\dfrac{\sigma}{\sqrt{n}}\)
Satunnaisesti valitun omenan paino \(X\)
\(X\sim N(159,12)\)
30 satunnaisesti valitun omenan keskipaino \(\bar{X}\)
\(\bar{X}\sim N\left(159,\dfrac{12}{\sqrt{30}}\right)\)
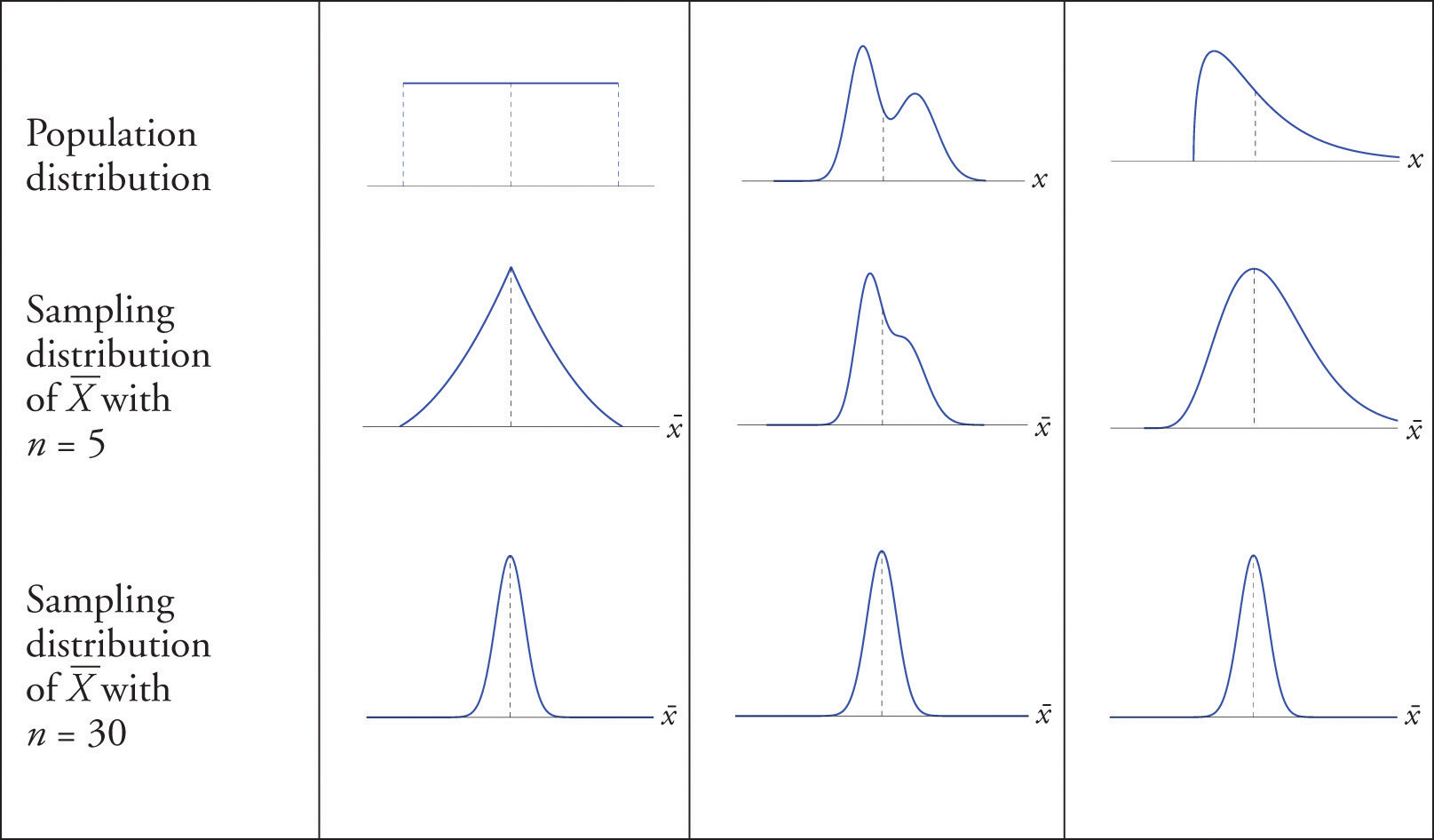
*Itseasiassa omenien painojen ei tarvitsisi olla edes normaalijakautuneita. Siltikin kun otetaan tarpeeksi monta omenaa ja lasketaan niiden painojen keskiarvo, tällaisten keskiarvojen jakauma on likimain normaalijakautunut
30 satunnaisesti valitun omenan keskipaino \(\bar{X}\)
\(\bar{X}\sim N\left(159,\dfrac{12}{\sqrt{30}}\right)\)
Millä todennäköisyydellä 30 satunnaisen valitun omenan keskipaino on enintään 156 g?
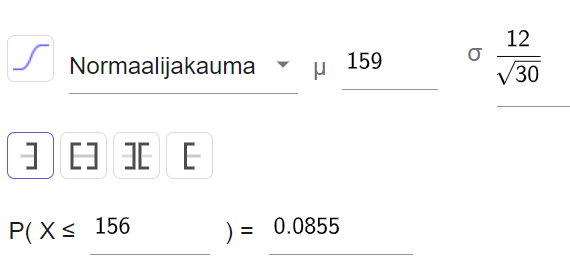
V: 8,6%
Millä symmetrisellä välillä sijaitsisi 95%
30 satunnaisesti valitun omenan keskipainoista?
Ts. mikä on sellainen luku \(a\), jolla \(P(159-a\leq \bar{X}\leq 159 + a)=0{,}95\)?
Satunnaisesti valitun omenan paino X
\(X\sim N(159,12)\)
30 satunnaisesti valitun omenan keskipaino Y
\(\bar{X}\sim N\left(159,\dfrac{12}{\sqrt{30}}\right)\)

Millä symmetrisellä välillä sijaitsisi 95%
30 satunnaisesti valitun omenan keskipainoista?
Ts. mikä on sellainen luku \(a\), jolla \(P(159-a\leq \bar{X}\leq 159 + a)=0{,}95\)?
Tutkitaan normitettua normaalijakaumaa!
Jos 95% on jakautunut symmetrisesti,
niin silloin vasemmalle jää 2,5% ja oikealle 2,5%.
Taulukosta voidaan lukea, että \(\Phi (-1{,}96)=0{,}025\) ja \(\Phi(1{,}96)=0{,}975\)
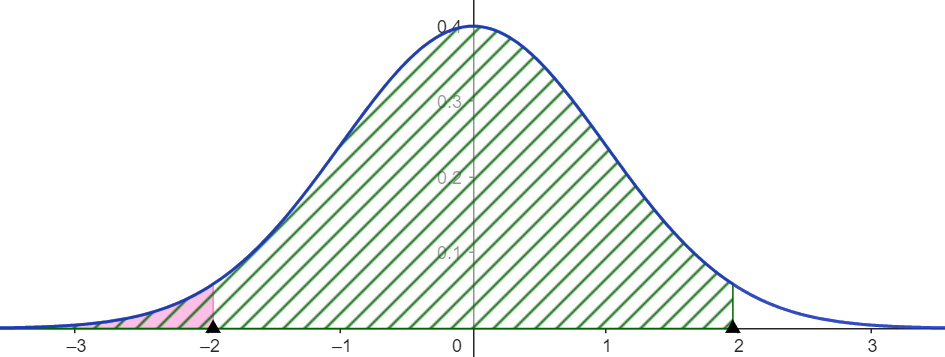
2,5%
2,5%
97,5%
\(\underbrace{\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad}\)
95%
Millä symmetrisellä välillä sijaitsisi 95%
30 satunnaisesti valitun omenan keskipainoista?
Ts. mikä on sellainen luku \(a\), jolla \(P(159-a\leq \bar{X}\leq 159 + a)=0{,}95\)?
Taulukosta voidaan lukea, että \(\Phi (-1{,}96)=0{,}025\) ja \(\Phi(1{,}96)=0{,}975\)
Siis normitetulle satunnaismuuttujalle \(Z\sim N(0,1)\)
\(P(-1{,}96\leq Z \leq 1{,}96)=0{,}95\)
Normitetusta arvosta \(z=\dfrac{x-\mu}{\sigma}\) voidaan ratkaista alkup. arvo \(x\)
\(x=\mu+z\sigma\)
Koska \(\mu=159\) ja \(\sigma=\dfrac{12}{\sqrt{30}}\),
\(P(159-1{,}96\cdot \dfrac{12}{\sqrt{30}} \leq \bar{X} \leq 159+1{,}96\cdot \dfrac{12}{\sqrt{30}})=0{,}95\)
\(P(\bar{X}-1{,}96\cdot \dfrac{12}{\sqrt{30}} \leq 159 \leq \bar{X}+1{,}96\cdot \dfrac{12}{\sqrt{30}})=0{,}95\),
joka antaa meille tavan laskea luottamusväli
Epäyhtälöä muokkaamalla äskeinen saadaan vielä muotoon
Normitetun normaalijakauman kertymäfunktion taulukosta löydetty luku 1,96 on luottamustason 95% kriittinen arvo \(z^*\)
Samalla tavalla voitaisiin päätellä minkä tahansa luottamustason kriittinen arvo
Yleisesti:
Luottamusväli saadan laskettua
\(\bar{x} \pm z^*\cdot s_{\bar{x}}\),
jossa \(\bar{x}\) on otoskeskiarvo, \(z^*\) luottamustasoa vastaava kriittinen arvo, \(s_{\bar{x}}=\dfrac{\sigma}{\sqrt{n}}\) keskiarvon keskivirhe ja \(n\) otoskoko.
("Tarpeeksi suurilla" \(n\) voidaan arvioida, että \(\sigma\approx s\))

Yleisimmät luottamusvälit löytyy MAOLista.
(Huom. MAOLissa merkintä \(s\) vastaa merkintää \(\sigma\))
Makeistehtaalla valmistetaan karkkeja, joiden painojen keskihajonta on 1,24 g. Yhteen pussiin valittiin satunnaisesti 25 karkkia, joiden keskipaino oli 8,24 g.
Laske karkkien painojen keskiarvon 99%:n luottamusväli.
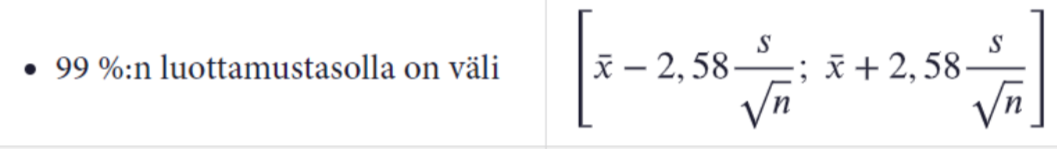
Alaraja:
\(8{,}24-2{,}58\cdot\dfrac{1{,}24}{\sqrt{25}}\approx7{,}60\)
Yläraja:
\(8{,}24+2{,}58\cdot\dfrac{1{,}24}{\sqrt{25}}\approx8{,}88\)
V: [7,60;8,88]
Huom. alaraja on hyvä pyöristää alaspäin ja yläraja ylöspäin, vaikka tavallinen pyöristyssääntö sanoisi muuta. Muuten pyöristämätön arvo ei kuulu välille.
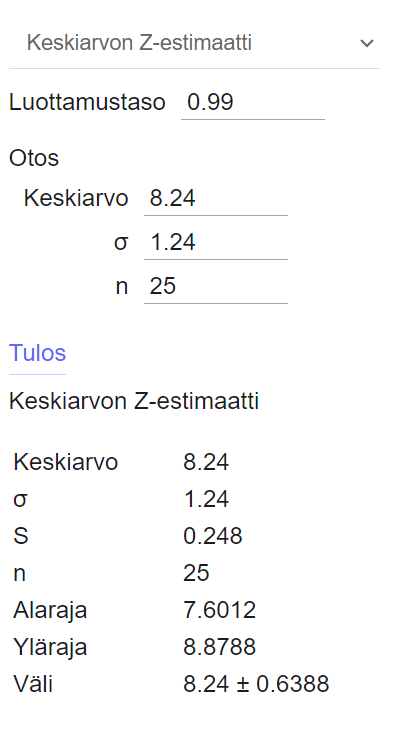
Huom. \(S=s_{\bar{x}}\), eli keskiarvon keskivirhe. Tämänkin voi katsoa Geogebrasta.
Sama luottamusväli saataisiin myös Geogebralla