Diskonttaus
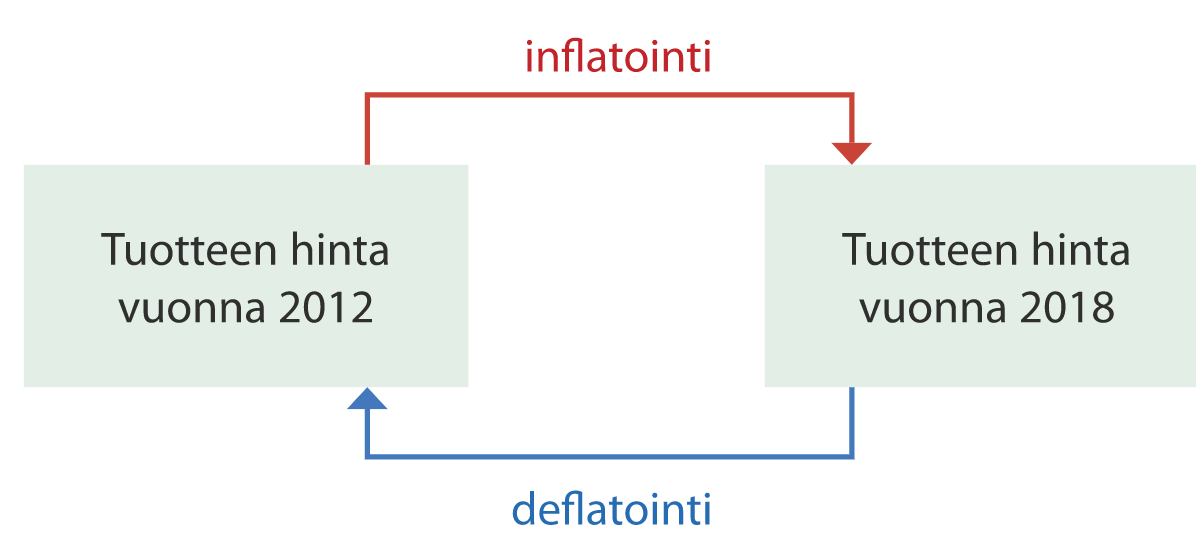
Rahan arvoa saatiin muutettua ajassa eteenpäin inflantoimalla ja ajassa taaksepäin deflatoimalla
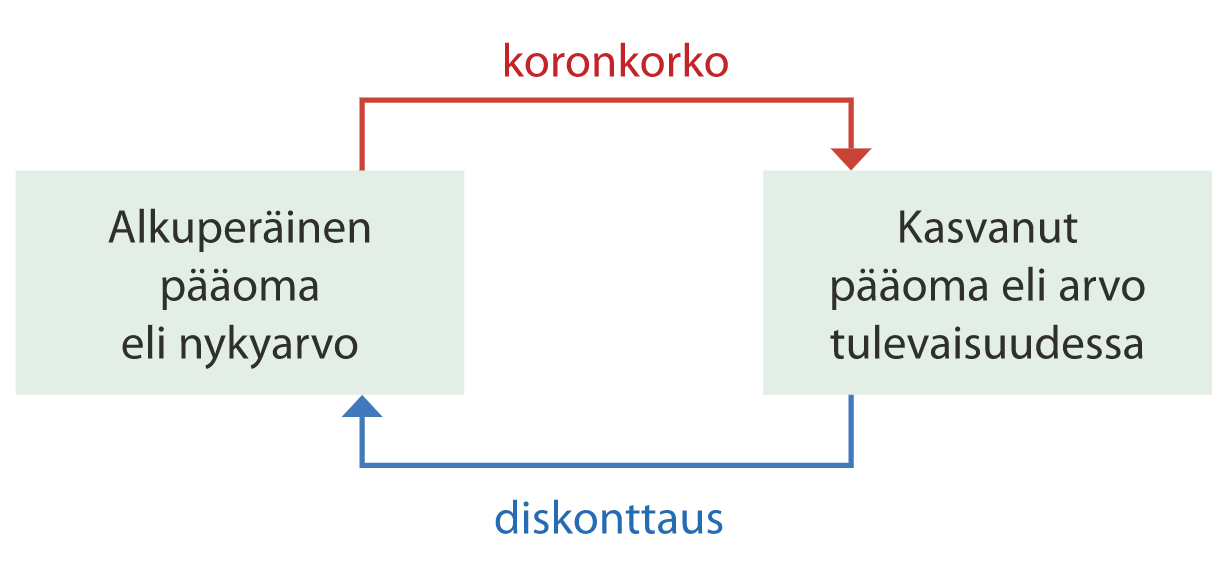
Vastaavasti asiaa voi miettiä pääomalle maksettavan koron kautta. Nykyisen pääoman arvo tulevaisuudessa saadaan laskettua korkolaskennan avulla, ja tulevaisuuden pääoman nykyarvo diskonttaamalla.
Diskonttaus eli nykyarvon laskeminen onnistuu ratkaisemalla alkuperäinen pääoma koronkoron kaavasta
Diskonttaaminen on käytännössä korkolaskentaa "takaperin":
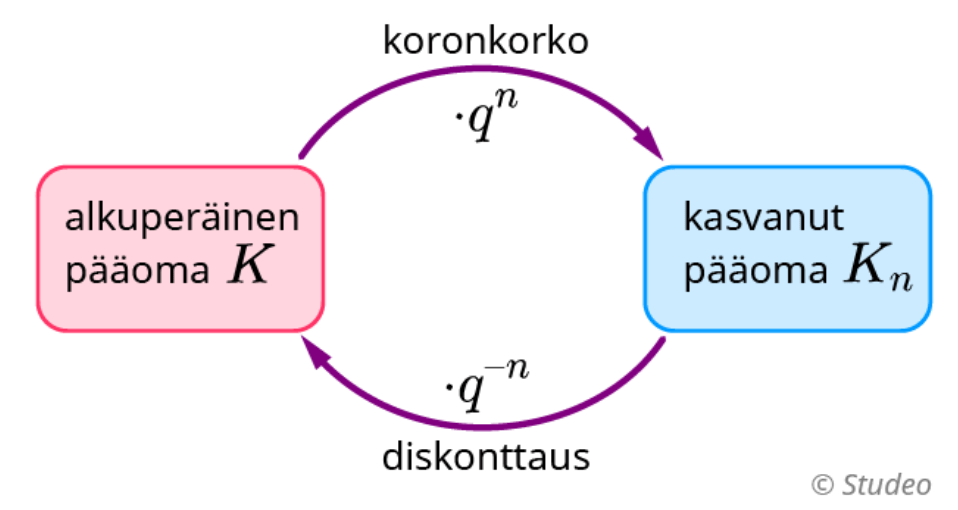
\(K=K_n \cdot q^{-n}\)
\(K_n=K \cdot q^{n}\)
Koronkorko:
Diskonttaus:
Mirkku haaveilee asuvansa 25 vuoden päästä "miljoonakodissa".
Minkä hintainen asunto hänen pitäisi nyt vähintään ostaa, jos oletetaan, että asunnon hinta nousee vuosittain 5%
\(K=K_n \cdot q^{-n}\)
\(n=25\), \(K_{25}=1\,000\,000€\), \(q=1+\dfrac{5}{100}=1{,}05\)
\(K=1\,000\,000€\cdot 1{,}05^{-25}\approx 300\,000€\)
Tapa 1: Diskonttaus
Tapa 2: Koronkorko
\(K_n=K \cdot q^{n}\)
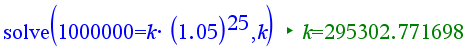
- Kun yritys investoi, se käyttää rahaa johonkin, jonka on tarkoitus tuottaa yritykselle voittoa myöhemmin
- Investointikohteita voi esim. olla tehdaskoneet tai työntekijöiden koulutus
- Jos yritys investoi omaa rahaa, investointi on kannattava vain, jos investoitava pääoma tuottaa enemmän kuin mitä se tuottaisi korkoina
- Ts. kaikkien odotettujen tulevaisuuden saatavien täytyy olla diskontattuna suuremmat kuin nyt investoitavan pääoman
- Sama pätee myös jos yritys investoi lainarahalla, koska investoinnin täytyy kattaa myös lainan korot
Pinjalla on pinssiyritys, joka valmistaa hienoja rintamerkkejä. Hän pohtii uuden 5000 euroa maksavan erikoispinssikoneen ostamista, jonka käyttöikä on n. 3 vuotta. Pinja arvioi, että pinssikone toisi lisätuloja yritykseen ensimmäisenä vuonna 1500€, toisena 1900€ ja kolmantena 2100€ (eli yht. 5500€). Kannattaako investointi, kun Pinja toisaalta olettaa saavansa sijoittamalla pääomalle korkoa 6,5%?
Selvitetään lisätulojen nykyarvo diskonttaamalla
\(1500€\cdot1{,}065^{-1}+1900€\cdot 1{,}065^{-2}+2100€\cdot 1{,}065^{-3}\approx4800€\)
Koska tulojen nykyarvo on vähemmän kuin mitä pinssikone maksaa, investointi ei kannata.