Eksponenttifunktio ja eksponentiaalinen malli
Kissavideolla on alussa 37 katselukertaa. Videosta tulee viraali, ja sen katselukerrat kaksinkertaistuvat joka päivä. Määritä funktio \(v(x)\), joka kertoo kissavideon katseluiden kokonaismäärän \(x\):n päivän päästä
| Päivä | Katselukerrat |
|---|---|
\(0\)
\(37\)
\(1\)
\(37\cdot 2\)
\(2\)
\(37\cdot 2\cdot 2\)
\(=37\cdot 2^2\)
\(3\)
\(37\cdot 2\cdot 2\cdot 2 = 37\cdot2^3\)
\(4\)
\(37\cdot 2\cdot 2\cdot 2\cdot2 = 37\cdot2^4\)
\(x\)
\(37\cdot2^x\)
\(v(x)=37\cdot2^x\)
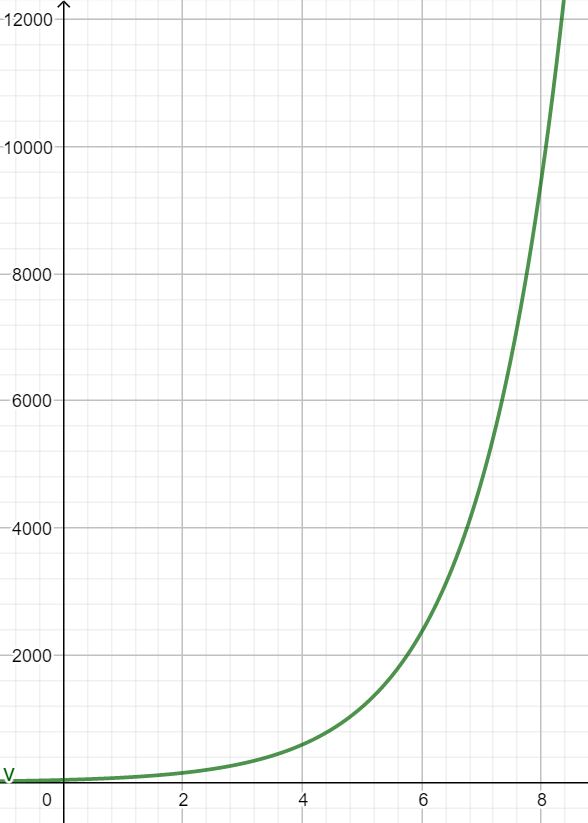
\(v(x)=37\cdot2^x\) on esimerkki eksponentiaalisesta mallista
Kuvaajasta nähdään, että viraalin videon katselumäärät kasvavat eksponentiaalisesti
Kissavideota katsotaan parhaimmillaan 43 000 kertaa päivässä. Tämän jälkeen uusien katselukertojen määrä pienenee joka päivä 13%. Määritä funktio \(n(x)\), joka kertoo uusien katselukertojen määrän \(x\) päivää huippupäivän jälkeen
| Päivä | Uudet katselukerrat |
|---|---|
\(0\)
\(1\)
\(2\)
\(3\)
\(4\)
\(43\,000\cdot 0{,}87\cdot 0{,}87\cdot 0{,}87\cdot 0{,}87 = 43\,000\cdot 0{,}87^4\)
\(x\)
\(43\,000\cdot 0{,}87^x\)
\(n(x)=43\,000\cdot 0{,}87^x\)
\(43\,000\cdot 0{,}87\cdot 0{,}87\cdot 0{,}87 = 43\,000\cdot 0{,}87^3\)
\(43\,000\cdot 0{,}87\cdot 0{,}87 = 43\,000\cdot 0{,}87^2\)
\(43\,000\cdot 0{,}87\)
\(43\,000\)
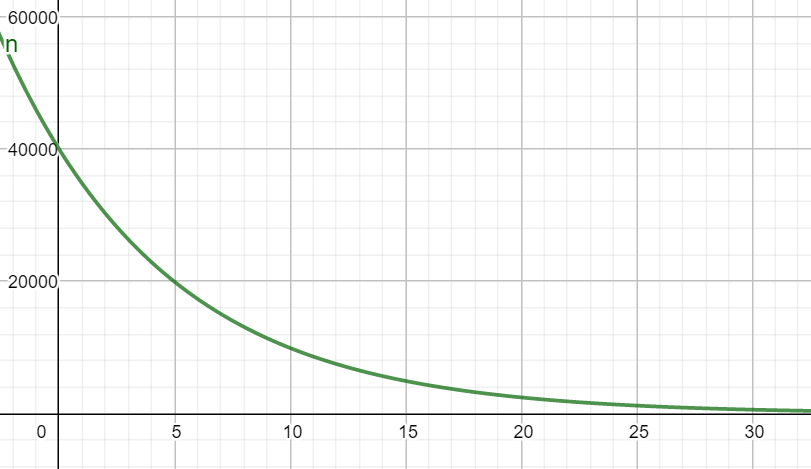
\(n(x)=43\,000\cdot 0{,}87^x\) on myös esimerkki eksponentiaalisesta mallista
Kuvaajasta nähdään, että uudet katselukerrat vähenevät eksponentiaalisesti
Funktiota \(f(x)=a^x\), jossa kantaluku \(a>0\) ja \(a\neq 1\), kutsutaan eksponenttifunktioksi
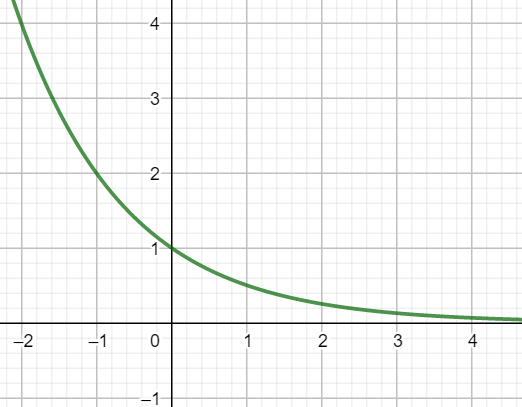
Jos \(0<a<1\),
funktio \(f\) on vähenevä
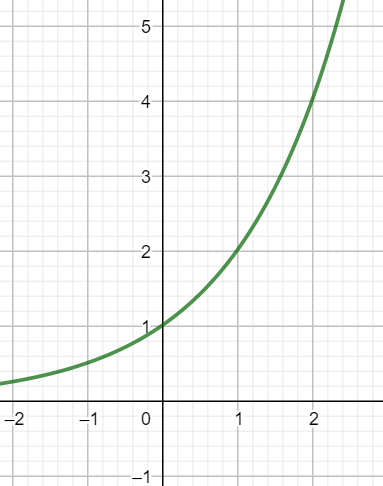
Jos \(a>1\),
funktio \(f\) on kasvava
Eksponentiaalisessa mallissa \(f(x)=Aq^x\)
lukua \(A\) kutsutaan alkuarvoksi
ja lukua \(q\) muutoskertoimeksi tai kantaluvuksi
Kun \(x=0\), niin \(f(0)=Aq^0 = A\cdot 1 = A\)
Siis funktion \(f\) kuvaaja leikkaa y-akselin aina pisteessä \((0,A)\)

\(n(x)=43\,000\cdot 0{,}87^x\)
\(A=43\,000\)
\(q=0{,}87\)
\((0,43\,000)\)