Newtonin menetelmä
Puolitusmenetelmä perustui funktion jatkuvuuteen. Entä jos funktio olisi myös derivoituva, auttaako tämä nollakohdan likiarvon määritämisessä?
\(x_1\)
\(x_2\)
- Arvioidaan nollakohdaksi ensiksi alkuarvaus \(x_1\)
- Piirretään tähän kohtaan tangentti
- Uudeksi arvioksi nollakohdalle saadaan tangentin ja x-akselin leikkauskohta
- Toistetaan kohtia 2 ja 3
\(x_3\)
Derivoituvan funktion \(f\) kohtaan \(x_1\) piirretyn tangentin kulmakerroin on \(f'(x_1)\), ja tangentilta löytyy piste \((x_1,f(x_1))\).
Suoran yhtälön kaavasta tangentin yhtälöksi saadaan:
\(y-f(x_1)=f'(x_1)(x-x_1)\)
Nollakohdassa \(y=0\), joten
\(-f(x_1)=f'(x_1)(x-x_1)\)
Kun yhtälöstä ratkaistaan \(x\), saadaan
\(x=x_1-\frac{f(x_1)}{f'(x_1)}\),
jossa \(x\) on uusi arvio nollakohdalle
\[x_n=x_{n-1}-\frac{f(x_{n-1})}{f'(x_{n-1})}\]
Iteroimalla saadaan Newtonin menetelmän kaava
\[x_n=x_{n-1}-\frac{f(x_{n-1})}{\underbrace{f'(x_{n-1})}_{\neq 0}}\]
Huom! Derivoituvuuden lisäksi täytyy olettaa, ettei derivaatta ole iteraatiokohdissa nolla, koska muuten jaettaisiin nollalla.
Lukujonon \((x_n)\) jäsenet voidaan laskea kätevimmin iteroimalla funktiota
\[g(x)=x-\frac{f(x)}{f'(x)}\]
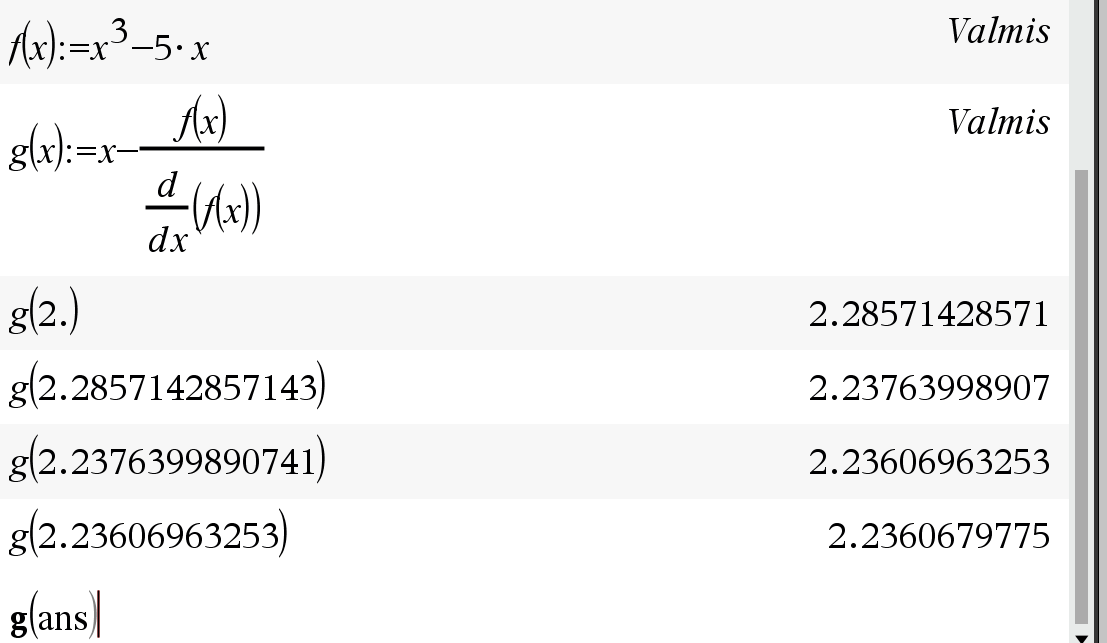
Funktion \(g(x)=x-\frac{f(x)}{f'(x)}\) iterointi nspiressä:
# Määritetään funktio Pythoniin
def f(x):
return x**3 - 5*x
# Määritetään funktion f derivaatta
def df(x):
return 3*x**2 - 5
# Määritetään iteroitava funktio g(x)
def g(x):
return x - f(x)/df(x)
# Asetetaan alkuarvaus
x = 2.0
for i in range(10):
x = g(x)
print("Nollakohdan likiarvo on x = " + str(x))Iterointi Pythonissa 10 kertaa:
Kuten puolitusmenetelmässäkin, alkuarvon valitsemiseksi on hyvä katsoa kuvaajaa, erityisesti jos funktiolla on useampi nollakohta
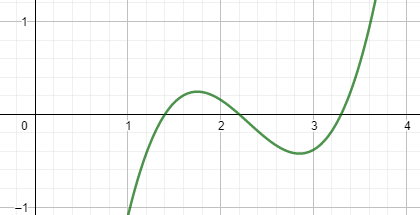
Nyrkkisääntönä alkuarvo pitäisi olla "riittävän lähellä" haluttua nollakohtaa, mutta kokeilemalla asia selviää helpoiten
Varoitus: aina Newtonin menetelmä ei suppene kohti mitään nollakohtaa