Potenssi
Samaan tapaan kuin yhteenlasku \(2+2+2\) voidaan esittää lyhyemmin kertolaskuna \(2\cdot 3\), kertolasku \(2\cdot 2\cdot 2\) voidaan esittää lyhyemmin potenssin avulla \(2^3\)
\(a^n=\underbrace{a\cdot a\cdot\ldots \cdot a}_{n \text{ kpl}}\), jossa \(n\in\mathbb{N}\)
kantaluku
eksponentti
Huom.
\(a^1 = a\)
\(a^0=1\)
Esim. \(4^3=4\cdot 4\cdot 4 = 64\)
Toista potenssia \(a^2\) kutsutaan luvun \(a\) neliöksi
Kolmatta potenssia \(a^3\) kutsutaan luvun \(a\) kuutioksi
\(3^1=3\)
\(\pi^0=1\)
\(2^1 = 2\)
\(2^2 = 4\)
\(2^3 = 8\)
\(2^4 = 16\)
\(\cdot 2\)
↷
\(\cdot 2\)
↷
\(\cdot 2\)
↷
\(\cdot 2\)
↷
\(\cdot 2\)
↷
\(\cdot 2\)
↷
↷
\(: 2\)
↷
\(: 2\)
↷
\(: 2\)
\(\cdot 2\)
↷
\(\cdot 2\)
↷
\(\cdot 2\)
↷
\(\cdot 2\)
↷
\(\cdot 2\)
↷
\(\cdot 2\)
↷
\(\cdot 2\)
↷
\(\cdot 2\)
↷
\(\cdot 2\)
↷
\(\cdot 2\)
↷
↷
\(: 2\)
↷
\(: 2\)
↷
\(: 2\)
↷
\(: 2\)
↷
\(: 2\)
\(2^0 = 1\)
\(2^{-1} = \frac{1}{2}\)
\(2^{-2} = \frac{1}{4}\)
\(2^{-3} = \frac{1}{8}\)
\(2^{-4} = \frac{1}{16}\)
\(a\neq 0\) ja \(n\) pos. kok. luku
\(a^0=1\)
\(a^{-n}=\dfrac{1}{a^n}\)
Eli miinus eksponentissa tarkoittaa käänteisluvun ottamista. Järjestyksellä ei ole väliä: voi korottaa ensiksi potenssiin ja ottaa käänteisluvun tai ottaa käänteisluvun ja korottaa potenssiin.
Erityisesti \(a^{-1}=\dfrac{1}{a}\)
\(=\left(\dfrac{1}{a}\right)^n\)
\(10^n=1~\underbrace{000\dots 000}_{n \text{ kpl}}\)
\(n\in\mathbb{N}\)
Suuria lukuja voidaan ilmaista kymmenpotenssien avulla
Luvulla \(10^n\) kertominen: siirretään pilkkua \(n\) askelta oikealle
Esim. \(3{,}2149\cdot 10^3 = 3214{,}9\)
Jos oikealla ei ole lukuja enempää, täytetään tyhjät kohdat nollilla
Esim. \(512{,}3\cdot 10^4 = 5~123~000\)
Jos luku on kokonaisluku, nollia lisätään eksponentin verran luvun loppuun
Esim. \(123\cdot 10^2 = 12~300\)
\(10^{-n}=\underbrace{0,000\dots 000}_{n \text{ kpl}}~1\)
Luvulla \(10^{-n}\) kertominen: siirretään pilkkua \(n\) askelta vasemmalle
Esim. \(1{,}23\cdot 10^{-5}=0{,}0000123\)
Kymmenpotenssin avulla saa esitettyä myös pieniä lukuja
Huom: kun luku esitetään kymmenpotenssimuodossa, halutaan, että kertoimessa pilkun vasemmalla puolella on yksi 0:sta poikkeava numero ja loput numerot pilkun oikealla puolella.
Siis \(1{,}23\cdot 10^{-5}\), ei \(12{,}3\cdot 10^{-6}\) tai \(0{,}0123\cdot 10^{-3}\).
Näin suuruusluokan hahmottaminen on helpompaa.
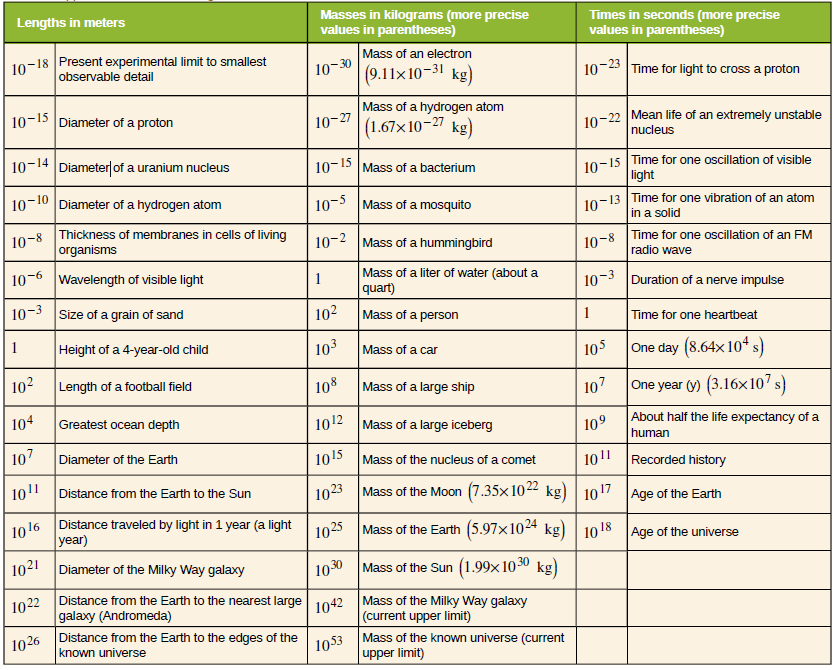
Lähde: OpenStax
\((ab)^n=\underbrace{ab\cdot ab \cdot \ldots \cdot ab}_{n\text{ kpl}}\)
Potenssin määritelmän mukaan
\((ab)^n=\underbrace{a\cdot a \cdot \ldots \cdot a}_{n\text{ kpl}}\cdot\underbrace{b\cdot b \cdot \ldots \cdot b}_{n\text{ kpl}}\)
Toisaalta tulontekijöiden järjestystä voidaan vapaasti muuttaa, jolloin
Potenssin määritelmää takaperin soveltaen saadaan tulon potenssin kaava
\((ab)^n=a^n b^n\)
Tulon potenssi on potenssien tulo
\[\left(\frac{a}{b}\right)^n = \underbrace{\frac{a}{b}\cdot\frac{a}{b}\cdot\ldots\cdot\frac{a}{b}}_{n\text{ kpl}}\]
\[\left(\frac{a}{b}\right)^n= \underbrace{\frac{a\cdot a \cdot \ldots \cdot a}{b\cdot b \cdot \ldots \cdot b}}_{n\text{ kpl}}\]
\[\left(\frac{a}{b}\right)^n=\frac{a^n}{b^n}\]
Potenssin määritelmästä:
Murtolukujen laskusäännöistä:
Potenssin määritelmästä saadaan osamäärän potenssin kaava
Osamäärän potenssi on potenssien osamäärä
\(a^m a^n = \underbrace{a\cdot\ldots\cdot a}_{m\text{ kpl}}\cdot \underbrace{a\cdot\ldots\cdot a}_{n\text{ kpl}}\)
\(a^m a^n = \underbrace{a\cdot\ldots\cdot a\cdot a\cdot\ldots\cdot a}_{m+n\text{ kpl}}\)
\(a^m a^n = a^{m+n}\)
Samankantaisten potenssien tulo ja osamäärä
\[\frac{a^m}{a^n} = \frac{\overbrace{\cancel{a}\cdot\cancel{a}\cdot\ldots\cdot \cancel{a}}^{n\text{ kpl}}\cdot \overbrace{a \cdot \ldots \cdot a}^{m-n\text{ kpl}}}{\underbrace{\cancel{a}\cdot\cancel{a}\cdot\ldots \cdot \cancel{a}}_{n \text{ kpl}}}\]
\(\frac{a^m}{a^n} = a^{m-n}\)
Potenssin potenssi
\[(a^m)^n=\underbrace{a^m\cdot \ldots \cdot a^m}_{n\text{ kpl}}\]
\[(a^m)^n=\underbrace{(\overbrace{a\cdot\ldots\cdot a}^{m\text{ kpl}})\cdot \ldots \cdot (\overbrace{a\cdot\ldots\cdot a}^{m\text{ kpl}})}_{n\text{ kpl}}\]
\[(a^m)^n = a^{mn}\]
Samat potenssikaavat toimivat sellaisenaan myös negatiivisille ja 0.:lle potenssille!
(Myöhemmillä kursseilla selviää, että ne ovat yleistettävissä myös eksponenteille, jotka ovat murtolukuja tai jopa irrationaalisia.)
Kaikki potenssikaavat löytyvät esim. MAOL:n taulukkokirjasta tai Abitin kaavakokoelmasta. (https://cheat.abitti.fi)