Tasalyhennyslaina
- Tasalyhennyslainassa lyhennetään eli maksetaan takaisin lainaa säännöllisesti samalla summalla, esim. 500 €/kk
- Lyhennyksen lisäksi joutuu maksamaan jäljellä olevasta
lainapääomasta korkoa korkokannan mukaan
Lainapääoma: 60 000€
Korkokanta: 3%
Laina-aika: 10v
Lyhennetään kuukausittain
Lainapääoma: 60 000€
Korkokanta: 3%
Laina-aika: 10v
Lyhennetään kuukausittain
Lyhennysten määrä:
\(12\cdot 10 = 120\)
Lyhennys:
\(\dfrac{60\,000€}{120}=500€\)
\(59\,500\cdot0{,}03\cdot\dfrac{1}{12}=148{,}75\)
\(500+150=650\)
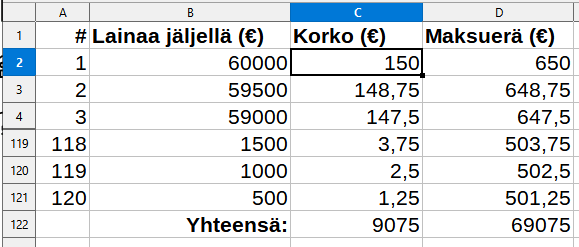
| # | Lainaa jäljellä | Korko (r = kit) (€) | Maksuerä (€) |
|---|---|---|---|
| 1. | 60 000 | ||
| 2. | 59 500 | ||
| 120. | 500 |
\(60\,000\cdot0{,}03\cdot\dfrac{1}{12}=150\)
\(500+148{,}75=648{,}75\)
\(500\cdot0{,}03\cdot\dfrac{1}{12}=1{,}25\)
\(500+1{,}25=501{,}25\)
\(59\,500\cdot0{,}03\cdot\dfrac{1}{12}=148{,}75\)
\(500+150=650\)
| # | Lainaa jäljellä | Korko (r = kit) (€) | Maksuerä (€) |
|---|---|---|---|
| 1. | 60 000 | ||
| 2. | 59 500 | ||
| 120. | 500 |
\(60\,000\cdot0{,}03\cdot\dfrac{1}{12}=150\)
\(500+148{,}75=648{,}75\)
\(500\cdot0{,}03\cdot\dfrac{1}{12}=1{,}25\)
\(500+1{,}25=501{,}25\)
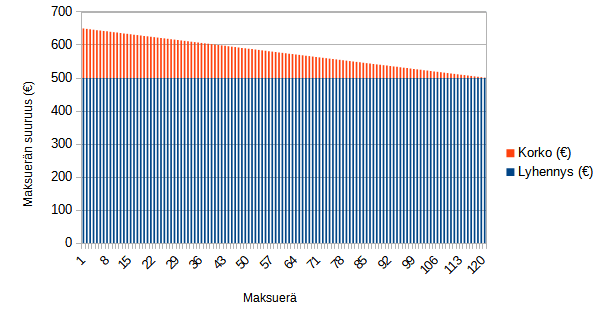
Tasalyhennyslainan korot muodostavat aritmeettisen jonon.
Korot voidaan siis laskea yhteen
aritmeettisen summan kaavalla \(S_n=n\cdot\dfrac{a_1+a_n}{2}\)
Yhteensä korkoja maksetaan
\(S_{120}=120\cdot\dfrac{150+1{,}25}{2}=9075\) (€)
Esimerkin 60 000€ lainasta maksetaan pankille takaisin siis \(60\,000€+9075€=69\,075€\)
Taulukkolaskimella:
Kaava solussa B3: =B2-500
Kaava solussa C2: =B2*0,03*1/12
Kaava solussa D2: =500+C2