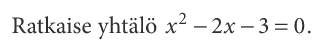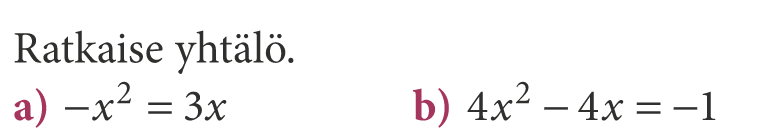Toisen asteen yhtälön ratkaisukaava
Ensimmäisen asteen yhtälöt saatiin kaikki muotoon \(ax+b=0\)
Ensimmäisen asteen yhtälö ratkeaa termejä siirtämällä ja kertoimia pois jakamalla. Halutessa voitaisiin kuitenkin johtaa "ensimmäisen asteen yhtälön ratkaisukaava"
\(ax+b=0\)
\(ax=-b\)
\[x=-\frac{b}{a}\]
\(\parallel :a\)
Nyt voidaan ratkaista esim. yhtälö \(2x+4=0\) käyttäen äskeistä ratkaisukaavaa
\[x=-\frac{4}{2}\]
Sijoitetaan \(a=2\) ja \(b=4\) kaavaan
\[x=-2\]
Tarkistus: \(2\cdot (-2) + 4 = -4 + 4 = 0\)
Kaikki toisten asteen yhtälöt saadaan muotoon \(ax^2+bx+c=0\)
Tällainen yhtälö ei ratkea pelkästään termejä siirtämällä ja kertoimia jakamalla. Toisen asteen yhtälön ratkaisemiseksi on onneksi kuitenkin ratkaisukaava