Functional Aggregate Design

Processes, Temporality & Automata Theory

Thomas Ploch

Principal Engineer @

https://twitter.com/tPl0ch

https://github.com/tPl0ch

https://www.linkedin.com/in/thomas-ploch-a3b79059/

With
Scala 3
Code
Examples

0. Outlook

0. Outlook

  1. Processes & Process Theories

  2. State Machines & Transducers

  3. Example Domain & Code

  4. Summary

1. Processes & Process Theories

1. Processes & Process Theories

Definition of a process

A process is a series or set of activities that interact to produce a result.

 

It may occur once-only or be recurrent or periodic.

https://en.wikipedia.org/wiki/Process

Definition of a process

1. Processes & Process Theories

A process is a series or set of activities that interact to produce a result.

 

It may occur once-only or be recurrent or periodic.

https://en.wikipedia.org/wiki/Process

sequential

parallel

goal-oriented

multiple actors

temporal

Definition of a process

1. Processes & Process Theories

Definition of a process theory

1. Processes & Process Theories

https://en.wikipedia.org/wiki/Process_theory

A process theory is a system of ideas that explains how an entity changes and develops.

Definition of a process theory

1. Processes & Process Theories

A process theory is a system of ideas that explains how an entity changes and develops.

https://en.wikipedia.org/wiki/Process_theory

made-up & unvalidated

communication tool

changes over time

Definition of a process theory

Variance theories focus on why something happens.

has identity

1. Processes & Process Theories

Dr. Arlyn Melcher (2013): https://drarlynmelcher.wordpress.com/traditional-variance-theory-dynamics-theory-and-process-theory/

structure

Process theories focus on how something happens.

Temporality in Process Theories

1. Processes & Process Theories

Temporality in Process Theories

1. Processes & Process Theories

Variance theories assume a static point in time and ask "Why are we here? What configuration of variables determined ending up in the observed state?"

Variance

System state at a specific point in time

Variable 1

Variable 2

Variable n

Process

Outcome 1

Outcome 2

Outcome 3

Outcome n

Process theories assume a longitudinal time and ask "How can we get there? What is the sequence of outcomes needed to arrive at the desired state?"

Time is longitudinal - it flows from left to right

1. Processes & Process Theories

Process Theory Archetypes

Process Theory Archetypes

Evolutionary

Explaining change in a population through variation, selection and retention. I.e. biological evolution.

1. Processes & Process Theories

Process Theory Archetypes

Evolutionary

Explaining change in a population through variation, selection and retention.

I.e. biological evolution.

Dialectic

Explaining stability and change by reference to the balance of power between opposing entities. I.e. "How would it be possible that Trump wins in 2024?".

1. Processes & Process Theories

Process Theory Archetypes

Evolutionary

Explaining change in a population through variation, selection and retention.

I.e. biological evolution.

Dialectic

Explaining stability and change by reference to the balance of power between opposing entities. I.e. "what would happen if Trump wins 2024?".

Teleological

Constructing an envisioned end state, taking action to reach it and monitoring the progress. I.e. forming a plan for a "Digital Transformation".

1. Processes & Process Theories

Process Theory Archetypes

Evolutionary

Explaining change in a population through variation, selection and retention.

I.e. biological evolution.

Dialectic

Explaining stability and change by reference to the balance of power between opposing entities. I.e. "how could it happen that Trump wins in 2024?".

Teleological

Constructing an envisioned end state, taking action to reach it and monitoring the progress. I.e. forming a plan for a "Digital Transformation".

Life-cycle

The trajectory to the final end state is prefigured and requires a particular historical sequence of events. Change always conforms to the same series of activities, stages, phases, like a caterpillar transforming into a butterfly.

Or a Software System!

1. Processes & Process Theories

Life-cycle

sequential

multiple actors

communication tool

temporal

made-up

changes over time

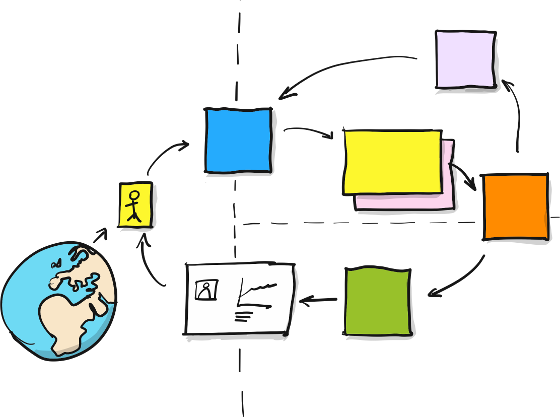
Image: Avanscoperta S.r.l https://www.avanscoperta.it/en/training/eventstorming-workshop-facilitation/

When we engage in modelling techniques like Event-Storming or Domain-Story-Telling,
we actually form
Lifecycle process theories!

Command

Aggregate

Event

Read
Model

Policy

has identity

1. Processes & Process Theories

structure

1. Processes & Life-cycle Process Theory

Definition of an Aggregate

...in the context of this presentation!

Aggregate implementations are small experiments to validate our life-cycle process theories, manifested in our systems as executable code.

1. Processes & Life-cycle Process Theory

Definition of an Aggregate

2. State Machines & Transducers

2. State Machines & Transducers

Definition of a State Machine

2. State Machines & Transducers

A Finite-State Machine (FSM) describes the processes during which information moves from one state to another for action, according to a set of rules. 

Definition of a State Machine

https://en.wikipedia.org/wiki/Finite-state_machine

2. State Machines & Transducers

A Finite-State Machine (FSM) describes the processes during which information moves from one state to another for action, according to a set of rules. 

Definition of a State Machine

https://en.wikipedia.org/wiki/Finite-state_machine

2. State Machines & Transducers

Definition of a State Machine

FSMs are sequential, event-driven and behavioral models that guarantee consistency and handle concurrency via the Run-To-Completion model.

It seems that they map very well to what we assume in our life-cycle process theories.

2. State Machines & Transducers

Definition of a State Machine

  • Are a great fit to model processes.
     
  • Drastically cut down the number of execution paths through the code.
     
  • Simplify the conditions at each branching point.
     
  • Lend themselves well to functional programming.

Using reactive programming without an underlying FSM model can lead to error prone, difficult to extend and excessively complex application code.

State Machines...

2. State Machines & Transducers

Limitations

There are no silver bullets!

2. State Machines & Transducers

Limitations

  1. Parallel processing
    Since (almost) all State Machine formalisms assume the RTC model (only one message can be processed at a time), there is no way to accommodate parallel processing. This would invalidate the machines' consistency guarantees.
     
  2. Supporting random ordering of messages
    All transitions have to be predefined, so scenarios in which messages can be received in any order result in a explosion of states that have to be encoded explicitly to represent all the possible combinations.

2. State Machines & Transducers

But what is a Transducer?

2. State Machines & Transducers

But what is a Transducer?

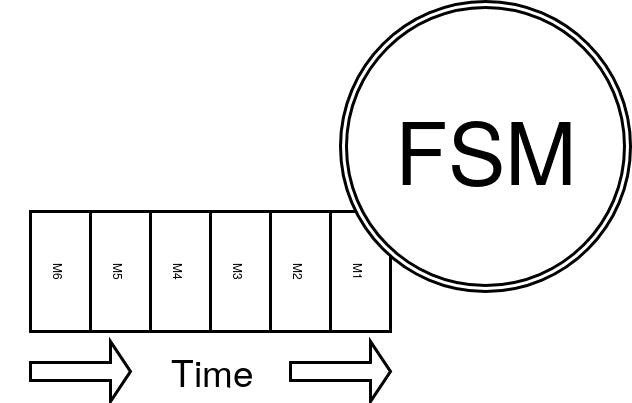
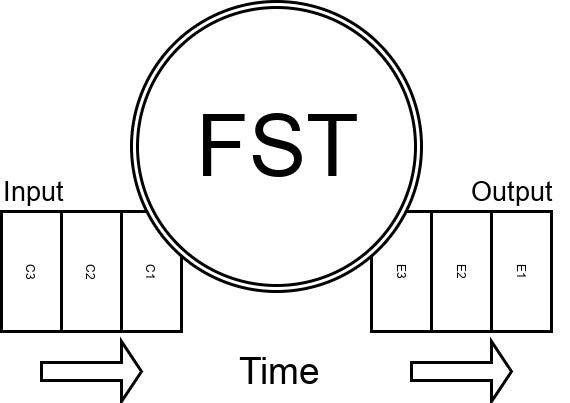
A FSM cannot provide any useful output, hence they are also called Acceptors - they can only determine if a sequence of inputs is valid.

A FST provides output signals in addition to state changes. That's what we need to send Events back to the system.

2. State Machines & Transducers

Mathematical Model

of a Transducer

2. State Machines & Transducers

Mathematical Model

T = \Big(S, C, E, \delta, \omega, S_0\colon S_0 \subset S, F\colon F \subset S \Big)

Initial State

Set of final States

\omega_{me} = S \times C \to E

Events (Mealy)

\delta = S \times C \to S

Behaviors

S

Set of States

C

Set of Commands

E

Set of Events

\omega_{mo} = S \to E

Events (Moore)

2. State Machines & Transducers

Process Modelling revisited

2. State Machines & Transducers

Command

Behaviors
Invariants

Event

Read
Model

Policy

When using process modelling techniques, Aggregates are often defined as a combination of:

  • Commands - stimuli from the environment
     
  • Behaviors - reactions to incoming stimuli that can change the Aggregate's response mechanisms
     
  • Invariants - rules that guarantee the logical consistency of the Aggregate
     
  • Events - system signals in response to changes in system state
     
  • Policies - external triggers that generate additional commands based on a set of rules

Process Modelling revisited

Image: Avanscoperta S.r.l https://www.avanscoperta.it/en/training/eventstorming-workshop-facilitation/

3. Example Aggregate

Account Registration

Account Registration

3. Example Aggregate

GIVE ME THE CODE ALREADY!

Encoding Life-cycles

3. Example Aggregate

Encoding Life-cycles

// A state before any lifecycle has started.
case object LifecycleNotStarted

// A function that determines the end
final type HasEnded[L] = L => Boolean

Life-cycles are distinct.
So we need a way to distinguish between multiple instances.

Start & End

3. Example Aggregate

// Either a life-cycle started and has an Identity,
// or it has not started.
type Identity[ID] = ID | LifecycleNotStarted.type

The ID type could be literally anything here,
since identifiers are extremely diverse across contexts!

Identities

3. Example Aggregate

Encoding Life-cycles

We also need a way to mark things as being part of a certain life-cycle, as well as comparing these to determine if they are part of the same life-cycle.

trait Lifecycle[ID] {
  def id: Identity[ID]
}

Life-cycles

3. Example Aggregate

Encoding Life-cycles

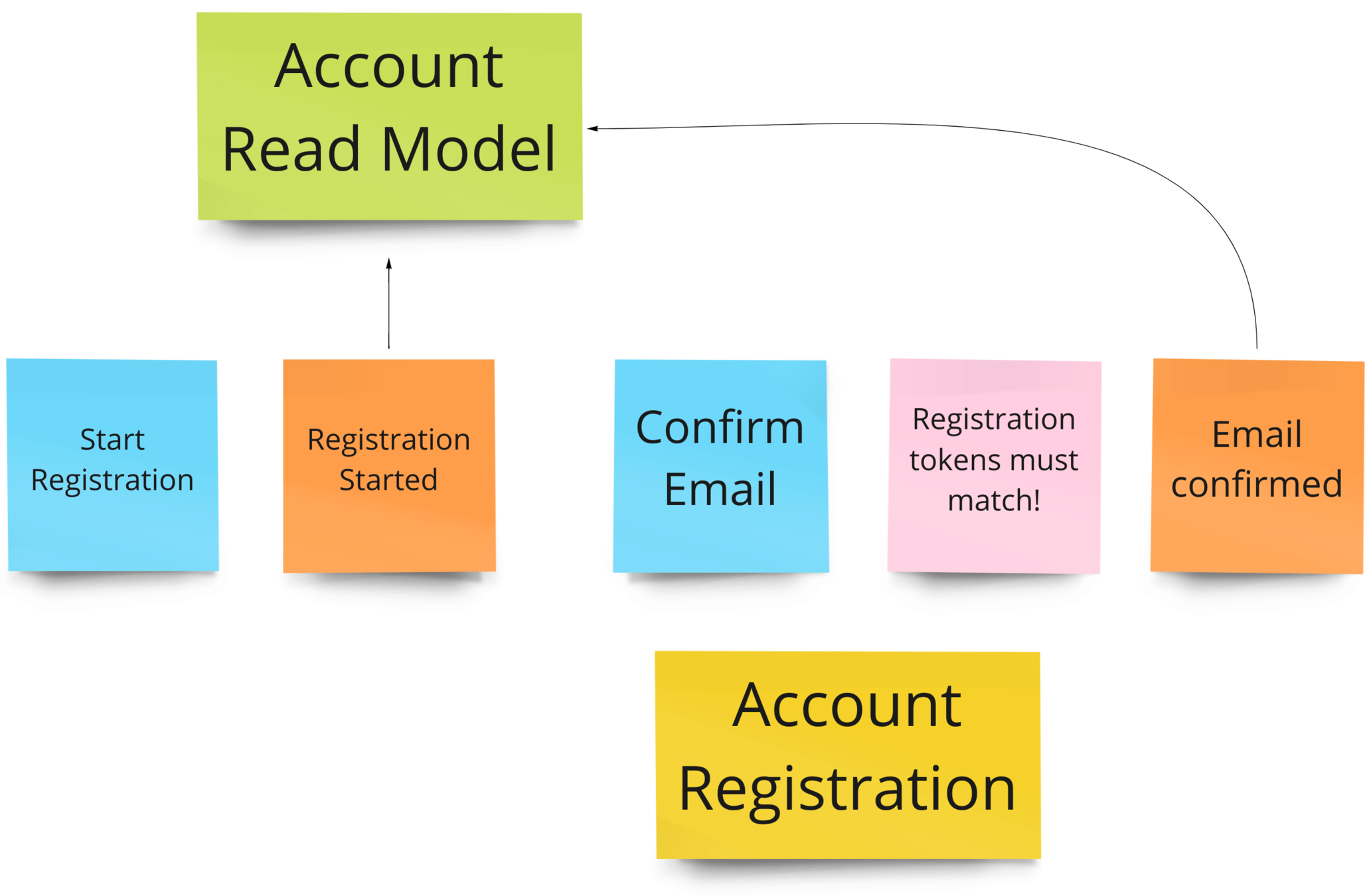
Account Registration Model

S

Set of States

C

Set of Commands

E

Set of Events

3. Example Aggregate

Account Registration Model

final case class AccountId(id: UUID)  extends AnyVal
final case class Email(value: String) extends AnyVal
final case class Token(value: String) extends AnyVal

enum Command extends Lifecycle[AccountId]:
  case StartRegistration(id: AccountId, email: Email, token: Token)
  case ConfirmEmail(id: AccountId, token: Token)

enum State extends Lifecycle[AccountId]:
  case PotentialCustomer(id: LifecycleNotStarted)
  case WaitingForEmailConfirmation(id: AccountId, email: Email, token: Token)
  case Active(id: AccountId, email: Email)

enum Event extends Lifecycle[AccountId]:
  case RegistrationStarted(id: AccountId, email: Email, token: Token)
  case EmailConfirmed(id: AccountId, email: Email)

3. Example Aggregate

Excursion: Generic Invariants

Account Registration Model

import cats.data.{ NonEmptyChain, Validated }

// Other than fail-fast monads,
// Validated can accumulate errors
type InvariantError[+EE <: Error, A] =
  Validated[NonEmptyChain[EE], A]

// Validates a (Command, State) pair
type Invariant[-C, -S, +EE <: Error] =
  PartialFunction[(C, S), InvariantError[EE, Unit]]

3. Example Aggregate

Cats - Scala library for functional primitives: https://typelevel.org/cats/

val tokensMustMatch: Invariant[C, S, EE] = {
  case (c: Command.ConfirmEmail, s: State.WaitingForEmailRegistration) =>
    if c.token.value != s.token.value
    then InvalidToken(c.token).invalidNec
    else ().validNec
}

Validating Registration Tokens

Account Registration Model

Invariants guard our model while behaviors represent valid transitions. Each invariant is testable in isolation.

3. Example Aggregate

Account Registration Model

\delta = S \times C \to S

Generic Behaviors

// A behavior is a partial function
type Behavior[-C, -S, EE <: Error] =
  PartialFunction[(C, S), InvariantError[EE, S]]

// Lifted Behavior in effect F
type BehaviorsK[F[_], -C, -S] = (C, S) => F[S]

3. Example Aggregate

Behaviors represent the core of our model - the actual state transitions.

Account Registration Model

val registration: Behavior[C, S, EE] = {
  case (c: Command.StartRegistration, _: State.PotentialCustomer) =>
    State.WaitingForEmailRegistration(c.id, c.email, c.token).validNec
}

val emailConfirmation: Behavior[C, S, EE] = {
  case (_: Command.ConfirmEmail, s: State.WaitingForEmailRegistration) =>
    State.Active(s.id, s.email).validNec
}
\delta = S \times C \to S

Behaviors

Each Behavior is testable in isolation, resulting in very small & focused test cases that reduce the cognitive load immensely.

3. Example Aggregate

def behaviors: BehaviorsK[EIO, C, S] =
  ((registration orElse
      (emailConfirmation << tokensMustMatch)
    ) << identitiesMustMatch
  ).liftLifecycleF

Account Registration Model

Composing Behaviors and Invariants

We can freely compose behaviors and invariants.

Then we lift the behaviors into an effectful Life-cycle.

3. Example Aggregate

def identitiesMustMatch[
  ID,
  C <: Lifecycle[ID],
  S <: Lifecycle[ID],
  EE <: Error
](using equalIdentities: Eq[Lifecycle[ID]])
      : Invariant[C, S, EE] = { case (c: C, s: S) =>
  if equalIdentities.eqv(c, s) then ().validNec
  else IdentitiesDoNotMatch(c, s).asInstanceOf[EE].invalidNec
}

Identity Invariant

The identitiesMustMatch invariant is a generic invariant that can be mixed in to validate that every new message's identity matches the state's identity.

Account Registration Model

3. Example Aggregate

\omega_{me} = S \times C \to E

Events (Mealy)

Account Registration Model

3. Example Aggregate

// Partial FN to produce an Output (Event)
type Output[-C, -S, +E] = PartialFunction[(C, S), E]

// Lifted Output FN in effect F
type OutputsK[F[_], -C, -S, +E] = (C, S) => F[E]
// Event when the registration has been started
val registrationStarted: Output[C, S, E] = {
  case (c: Command.StartRegistration, _: State.PotentialCustomer) =>
    Event.RegistrationStarted(c.id, c.email, c.token)
}

// Event when the registration has been completed
val emailConfirmed: Output[C, S, E] = {
  case (_: Command.ConfirmEmail, s: State.WaitingForEmailRegistration) =>
    Event.EmailConfirmed(s.id, s.email)
}
\omega_{me} = S \times C \to E

Events (Mealy)

Account Registration Model

3. Example Aggregate

def events: OutputsK[EIO, C, S, E] =
  (registrationStarted orElse emailConfirmed)
    .liftF
\omega_{me} = S \times C \to E

Events (Mealy)

Account Registration Model

3. Example Aggregate

Again, similar to our behaviors,
we can freely compose our event outputs.

Account Registration Model

// Pure state
type State[S] = S => S

// Pure State with Event
type StateE[S, E] = S => (S, E)

// Effectful State with Event
type StateF[F[_], S, E] = S => F[(S, E)]

A short note on functional State...

3. Example Aggregate

Account Registration Model

// Re-using the type defined in the Life-cycle section
// Automatically resolved implicit fn for the model
given isFinalState: HasEnded[State] with
  override def apply(s: State): Boolean = s match
    case _: State.Active => true
    case _               => false
F\colon F \subset S

Set of final States

3. Example Aggregate

We create an implicit instance of HasEnded[State] for our model to indicate the end of the life-cycle.

Transducer

// A Transducer is now a function
// of a Command to a new StateF
type FST[F[_], -C, -S, +E] = C => StateF[F, S, E]

// A FSM can easily represented
// by setting the Event type to Unit
type FSM[F[_], C, S] = FST[F, C, S, Unit]
T = \Big(S, C, E, \delta, \omega, S_0\colon S_0 \subset S, F\colon F \subset S \Big)

3. Example Aggregate

Transducer

Now we can finally construct our Aggregate!

object Aggregate {
  def apply[F[_], C, S, E](
      behaviors: BehaviorsK[F, C, S],
  )(outputs: OutputsK[F, C, S, E])(using Monad[F])
      : FST[F, C, S, E] =
    (c: C) =>
      StateF { (s: S) =>
        for {
          newState <- behaviors(c, s)
          event    <- outputs(c, s)
        } yield (newState, event)
      }
}

Account Registration Model

Constructing our Aggregate

3. Example Aggregate

  // FSMs only need behaviors
  val registrationStateMachine: StateMachine =
    Aggregate(behaviors)
  
  // FSTs need behaviors and events
  val registrationTransducer: Transducer =
    Aggregate(behaviors)(events)

Account Registration Model

Constructing our Aggregate

3. Example Aggregate

Illustrating some Use-Cases

3. Example Aggregate

Illustrating some Use-Cases

val stateStoringRegistration: StateMachine = command =>
  for {
    newState <- registrationStateMachine(command).get
    _        <- StateT.liftF(saveState[EIO](newState))
  } yield ()

Storing only the current state

We compose executing the next behavior with a command, getting the next state and storing the state.
This will yield another State Machine.

3. Example Aggregate

Illustrating some Use-Cases

val programEIO: (UID[AccountId], Seq[C]) => EIO[S] =
  (uid, commands) =>
    for {
      initialState <- loadState[EIO](uid)
      currentState <- stateStoringRegistration
        .runAllState(commands)(initialState)
    } yield currentState

Storing only the current state

In order to construct our final program, we only need to load the initial state from the store. Then we process an identity stream of commands with the State Machine and yield the result.

3. Example Aggregate

Illustrating some Use-Cases

val storeAndPublish = (s: State, e: Event) =>
  StateT.liftF(for {
    _ <- saveState[EIO](s)
    _ <- transactionalOutbox[EIO](e)
  } yield ())

State store & Event publishing

3. Example Aggregate

We make use of the Transactional Outbox pattern and compose the state store and publish actions together. 

Transactional Outbox: https://microservices.io/patterns/data/transactional-outbox.html

Illustrating some Use-Cases

val eventPublishingRegistration: Transducer =
  command =>
    // Run the transducer with the command
    val stateT = registrationTransducer(command)

    for {
      event <- stateT
      state <- stateT.get
      _     <- storeAndPublish(state, event)
    } yield event

3. Example Aggregate

State store & Event publishing

Illustrating some Use-Cases

val programEIO: (UID[AccountId], Seq[C]) => EIO[Seq[E]] =
  (uid, commands) =>
    for {
      initialState <- loadState[EIO](uid)
      listOfEvents <- eventPublishingRegistration
        .runAllEvents(commands)(initialState)
    } yield listOfEvents

The final program almost looks almost exactly the same as in the previous example, only that we now run .runAllEvents instead of .runAllState and now get a list of published events instead of a single state as a result.

3. Example Aggregate

State store & Event publishing

Illustrating some Use-Cases

val reconstitution: (E, S) => InvariantError[EE, S] = { 
  case (e, s) => (e, s) match
    case (
      rs: Event.RegistrationStarted,
      _: State.PotentialCustomer,
    ) =>
      State.WaitingForEmailRegistration(
        rs.id, rs.email, rs.token
      ).validNec
    case _ => CannotReconstituteFrom(e, s).invalidNec
}

Event Sourcing

The first thing we need is a reconstitution function that can determine new states from an Event E and a State S.

3. Example Aggregate

Illustrating some Use-Cases

val eventStoringAggregate: Transducer = command =>
  for {
    newEvent <- registrationTransducer(command)
    _        <- StateT.liftF(saveEvent[EIO](newEvent))
  } yield newEvent

We again compose a new Transducer with the capability to store each new event after the Transducer has processed the next command.

3. Example Aggregate

Event Sourcing

Illustrating some Use-Cases

val programEIO: (UID[ID], Seq[C]) => EIO[Seq[E]] =
  (uid, commands) =>
    for {
      (snapshot, events) <- loadEventStream[EIO](uid)
      sourcedState <-
        reconstituteState[EIO](reconstitution)(snapshot)(events)
      newEvents <- eventStoringAggregate
        .runAllEvents(commands)(sourcedState)
    } yield newEvents

The final program consists of loading the latest event stream with its snapshot and reconstituting the current initial state for the Transducer. Afterwards its again running the Transducer with the commands and initial state.

3. Example Aggregate

Event Sourcing

Illustrating some Use-Cases

In any of the use-cases, we didn't modify the model to accommodate for the different modes of operation.

3. Example Aggregate

The FST Aggregate always represents the smallest unit in the composition hierarchy.

4. Summary

4. Summary

  • Using process modelling techniques like Event Storming or Domain Story Telling means forming life-cycle process theories, and Aggregates can be viewed as small-scale experiments to validate our theories.

  • State machines & Transducers are a great way to model life-cycle processes, since they are temporal, behavioral & event-driven models that reduce complexity and give strong guarantees around consistency and concurrency via the Run-To-Completion execution model. But they also have limitations around parallel processing and randomly ordered messages.

  • Taking the mathematical definition of a Transducer, we implemented a functional Aggregate following the definition closely, making use of Life-cycles, Identities, Invariants, Behaviors and Events.

  • We put the example Aggregate to the test and implemented various use cases via composition - i.e. State Store, Event-Publishing and Event-Sourcing.

Thank You!

Code examples @ GitHub

https://github.com/tPl0ch/ddd-process-time-state

We are hiring @

https://flix.careers

Presentation Slides @

https://slides.com/tploch/functional-aggregate-design

2. State Machines & Transducers

Behaviors & Invariants

2. State Machines & Transducers

Behaviors & Invariants

import cats.data.{ NonEmptyChain, Validated }

// Other than fail-fast monads,
// Validated can accumulate errors
type InvariantError[+EE <: Throwable, A] =
  Validated[NonEmptyChain[EE], A]

// Validates a (Command, State) pair
type Invariant[-C, -S, +EE <: Throwable] =
  PartialFunction[(C, S), InvariantError[EE, Unit]]

Cats - Scala library for functional primitives: https://typelevel.org/cats/

2. State Machines & Transducers

Behaviors & Invariants

import cats.data.Kleisli

// A behavior needs to validate the input label
type Behavior[-C, -S, EE <: Error] =
  PartialFunction[(C, S), InvariantError[EE, S]]

// Lifted Behavior in effect F
type BehaviorsK[F[_], -C, -S] = (C, S) => F[S]

Cats - Scala library for functional primitives: https://typelevel.org/cats/

\delta = S \times C \to S

Behaviors

2. State Machines & Transducers

Behaviors & Invariants

extension [F[_], C, S]
    (behaviors: BehaviorK[F, C, S])

  def onlyWhenLifecycleIsActive(using
      F: ApplicativeThrow[F],
      thisIsTheEnd: Lifecycle.HasEnded[S],
  ): BehaviorK[F, C, S] =
    (c: C, s: S) =>
      if !thisIsTheEnd(s)
      then behaviors((c, s))
      else F.raiseError(LifecycleHasEnded(c, s))

2. State Machines & Transducers

Events

2. State Machines & Transducers

Events

// Produce an event
type Output[-C, -S, +E] =
  PartialFunction[(C, S), E]

// Lifted output in effect F
type OutputsK[F[_], -C, -S, +E] =
  (C, S) => F[E]

Cats - Scala library for functional primitives: https://typelevel.org/cats/

\omega = S \times C \to E

Event Function

2. State Machines & Transducers

Functional State

2. State Machines & Transducers

Functional State

// Pure state
type State[S] = S => S

// Pure State with Event
type StateE[S, E] = S => (S, E)

// Effectful State with Event
type StateF[F[_], S, E] => S => F[(S, E)]

Cats - Scala library for functional primitives: https://typelevel.org/cats/

2. State Machines & Transducers

Transducer

2. State Machines & Transducers

Transducer

object Transducer {
  def apply[F[_], C, S, E](behaviors: BehaviorsK[F, C, S])(
    events: OutputsK[F, C, S, E],
  )(using F: MonadThrow[F], E: Lifecycle.HasEnded[S])
      : FST[F, C, S, E] =
    (c: C) =>
      StateF { (s: S) =>
        for {
          newState <- behaviors.onlyWhenLifecycleIsActive(c, s)
          event    <- events(c, s)
        } yield (newState, event)
      }

Cats - Scala library for functional primitives: https://typelevel.org/cats/

2. State Machines & Transducers

Transducer

extension [F[_], C, S, E](transducer: FST[F, C, S, E])
  def run(command: C)(state: S)(using F: Functor[F]): F[E] =
    transducer(command).runA(state)

  def traverse(commands: List[C])(using F: Monad[F])
      : StateF[F, S, List[E]] =
    commands.foldLeft(StateF.liftF(F.pure(Nil: List[E]))) {
      (stateF, command) =>
        for {
          acc   <- stateF
          event <- transducer(command)
        } yield acc.appended(event)
    }

Cats - Scala library for functional primitives: https://typelevel.org/cats/

Type aliases for better usability

3. Example Domain

object Types {
  type EIO[A] = EitherT[IO, NonEmptyChain[RegistrationError], A]
  type ID     = AccountId
  type C      = Command
  type S      = State
  type E      = Event
  type R      = ReadModel.Account
  type EE     = RegistrationError

  type StateMachine = FSM[EIO, C, S]
  type Transducer   = FST[EIO, C, S, E]
  type Projection   = FST[EIO, C, S, R]
}