Applied

Microeconomics

Lecture 22

BE 300

Plan for Today

Case

Finish price discirmination

Multi-part pricing

Coming Up

"Bundles of Joy" Case Due Next Week

Textbook reading 10.5-10.7

Scholarly Communication

Application to Academic Journal Pricing

•Prices for the Royal Economic Society’s Economic Journal:

Scholarly Communication

•MCs of printing and delivering the journal to a subscriber are $20/year, whether the subscription is sent to the U.S. or UK

•The fixed costs of soliciting, editing and typesetting articles for the journal are $260,000 annually; If the EJ shuts down temporarily, these fixed costs can be avoided

•What are the optimal prices in the United Kingdom & the United States (assuming monopoly), if the markets can be segmented?

Scholarly Communication

Q_{US} = 8000 - 50 P_{US} \quad \text{or} \quad P_{US} = 160 - 0.02 Q_{US}

Q ​ U S ​ ​ = 8000 - 50 P ​ U S ​ ​ o r P ​ U S ​ ​ = 160 - 0.02 Q ​ U S ​ ​

Q_{UK} = 1000 - 10P_{UK} \quad \text{or} \quad P_{UK} = 100 - 0.1 Q_{UK }

Q ​ U K ​ ​ = 1000 - 10 P ​ U K ​ ​ o r P ​ U K ​ ​ = 100 - 0.1 Q ​ U K ​ ​

US demand:

UK demand:

Q1 & Q2: Draw and label the (linear) UK and U.S. demand curves. Calculate the profit maximizing price and quantity of subscriptions for the United Kingdom, and indicate each on the appropriate graph. Do the same for the United States.

Scholarly Communication

If you can segment: Set MC = MR in both markets (one at a time)

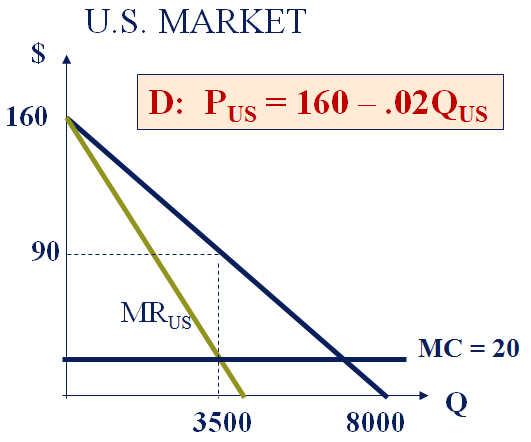
Marginal Revenue--demand curve + twice the slope. So in the US:

160-0.04Q=20

Q=3500, P=90

Scholarly Communication

If you can segment: Set MC = MR in both markets (one at a time)

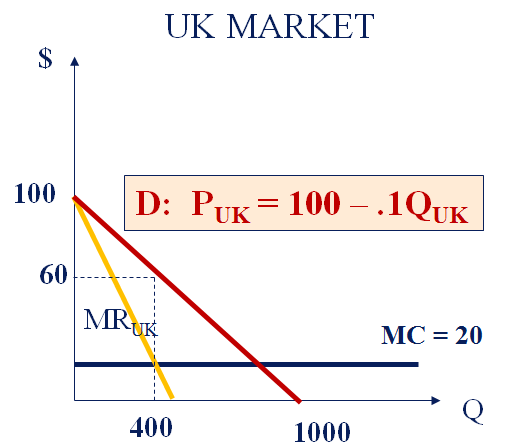
In the UK--

MR=100-0.2Q = 20

Q=400, P=60

Given the price in the US is so much higher, can't RES increase profits by re-allocating some of its sales to the US from the UK?

Scholarly Communication

Calculate total profits:

Costs

Fixed Cost = 260,000/year

MC = AVC = 20

TC = 260,000 + 20(3500 + 400) = $338,000

Revenue

TR = PUS x QUS + PUK x QUK

= 90 x 3500 + 60 x 400 = $339,000

Profit = 339,000 – 338,000 = $1,000

Scholarly Communication

What if RES was not allowed to price discriminate?

•If the RES were forced to charge the same price to all subscribers, the profit maximizing price per subscription would be $85.00.

•If $85 is the best single price the RES can get for its journal, what level of output should the RES plan for next year?

US demand: QUS = 8000 – 50PUS (or, PUS = 160 – 0.02QUS )

•UK demand: QUK = 1000 – 10PUK (or, PUK = 100 – 0.1QUK )

•How much could RES sell at P = 85?

~QUS = 8000 – 50 * (85) Þ QUS = 3750

~QUK = 1000 – 10 * (85) Þ QUK = 150

~Q = QUS + QUK = 3750 + 150 = 3900

Scholarly Communication

So, how much should RES sell if the maximum profit occurs at P=$85?

•Check profits:

~TR = 3900(85) = $331,500

~Per Unit Operating Costs = 20 * 3900 = 78,000

~Operating Profits = TR – VC = $253,500

~Next Year (when annual costs are not yet spent)?

–TC = 260,000 + 20 (3900) = $338,000

–Profit = TR – TC = – $6,500 => shut down

–Answer = RES should sell NO subscriptions at $85

•Eliminating differential pricing will leave readers worse off because the firm will shut down.

•RES would choose to produce zero (since the $260,000 is not sunk – it is avoidable cost).