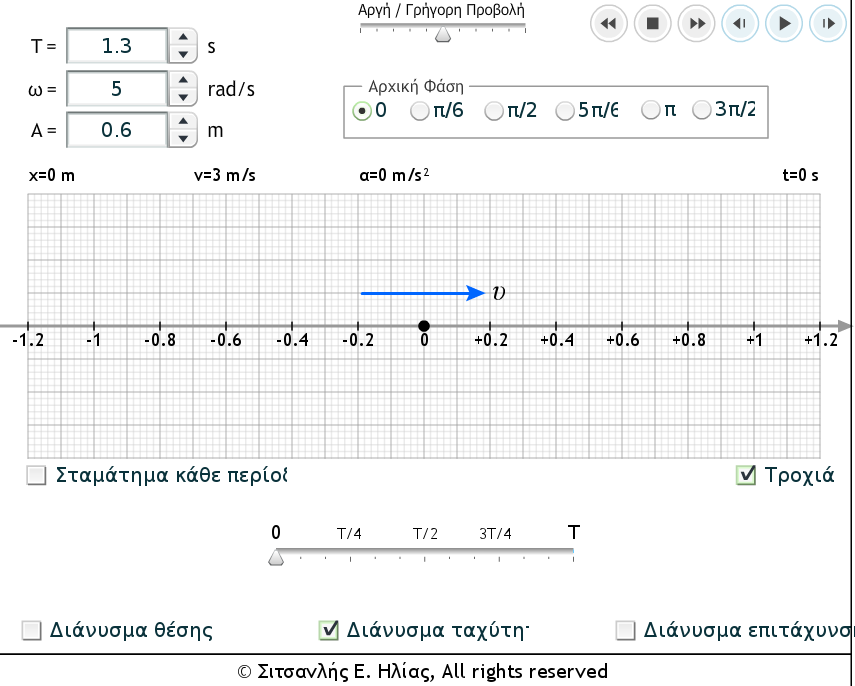
Απλή Αρμονική Ταλάντωση

Χαρακτηριστικές Θέσεις & Μεγέθη Ταλάντωσης

  • Θέση Ισορροπίας  (...εκεί όπου...)

 

  • Απομάκρυνση από την Θ.Ι. , "Πλάτος" ...

 

  • Περίοδος, συχνότητα, κυκλική συχνότητα ...

 

  • Φάση ταλάντωσης ...

 

  • Ταχύτητα, επιτάχυνση...
\sum \vec{F}=0
∑F⃗=0\sum \vec{F}=0
\vec x , A
x⃗,A\vec x , A
\ T, f, \omega
 T,f,ω\ T, f, \omega
\omega \cdot t + \varphi_o
ω⋅t+φo\omega \cdot t + \varphi_o
\vec \upsilon , \vec a
υ⃗,a⃗\vec \upsilon , \vec a

Συνθήκη για αμείωτη α.α.τ

Στην τυχαία θέση,

το αντικείμενο που ταλαντώνεται δέχεται συνισταμένη δύναμη ανάλογη της απομάκρυνσης, με κατεύθυνση προς την Θ.Ι.

όπου D , η σταθερά επαναφοράς που εξαρτάται από το είδος του ταλαντωτή (π.χ. στο σύστημα ελατήριο μάζα, D = k)

\color{Blue}{\sum F=-D\cdot x}
∑F=−D⋅x\color{Blue}{\sum F=-D\cdot x}

Εξισώσεις

  • Η μέγιστη ταχύτητα ταλάντωσης 
\color{Green}{x=A\cdot \eta \mu (\omega t+\varphi _o)}
x=A⋅ημ(ωt+φo)\color{Green}{x=A\cdot \eta \mu (\omega t+\varphi _o)}
\color{Blue}{\upsilon =\color{Red}{\omega A}\cdot\sigma \upsilon \nu (\omega \cdot t+\varphi _o)}
υ=ωA⋅συν(ω⋅t+φo)\color{Blue}{\upsilon =\color{Red}{\omega A}\cdot\sigma \upsilon \nu (\omega \cdot t+\varphi _o)}
\alpha=-\omega^2\color{Green}{A\cdot \eta \mu (\omega t+\varphi _o)}
α=−ω2A⋅ημ(ωt+φo)\alpha=-\omega^2\color{Green}{A\cdot \eta \mu (\omega t+\varphi _o)}
\color{Red}{\omega \cdot \ A = \upsilon_{max}}
ω⋅ A=υmax\color{Red}{\omega \cdot \ A = \upsilon_{max}}
  • Η μέγιστη επιτάχυνση
\omega^2 \cdot \ A = \alpha_{max}
ω2⋅ A=αmax\omega^2 \cdot \ A = \alpha_{max}
\alpha=-\omega^2\cdot \color{Green}{\ x}
α=−ω2⋅ x\alpha=-\omega^2\cdot \color{Green}{\ x}

ή

Διαγράμματα

  • Τα μεγέθη α,υ,x, διαφέρουν μεταξύ τους κατά π/2:
\alpha \rightarrow^{\pi /2}\upsilon \rightarrow^{\pi / 2}x
α→π/2υ→π/2x\alpha \rightarrow^{\pi /2}\upsilon \rightarrow^{\pi / 2}x
  • Η απομάκρυνση και η επιτάχυνση βρίσκονται σε αντίθεση φάσης
Επιπλέον...

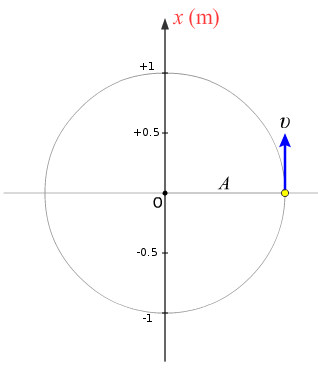
ο τριγωνομετρικός κύκλος / στρεφόμενα διανύσματα

Αναπαράσταση της ταλάντωσης με ένα στρεφόμενο διάνυσμα μήκους Α, που στρέφεται με γωνιακή ταχύτητα ω

Σχέσεις μεγεθών - Γραφικές παραστάσεις

  • Σταθερά επαναφοράς:
D = m\cdot \omega ^2
D=m⋅ω2D = m\cdot \omega ^2
  • Περίοδος ταλάντωσης:
T=2\cdot{\pi}\sqrt{m\over{D}}
T=2⋅πmDT=2\cdot{\pi}\sqrt{m\over{D}}

Διάγραμμα Φάσης - Χρόνου

Διάγραμμα Δύναμης Επαναφοράς  - Απομάκρυνσης

\phi=\omega \cdot t + \varphi_o
ϕ=ω⋅t+φo\phi=\omega \cdot t + \varphi_o
F_{\epsilon \pi} = -D \cdot x
Fϵπ=−D⋅xF_{\epsilon \pi} = -D \cdot x

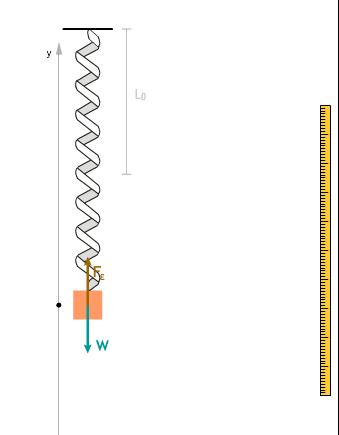
ΕΦΑΡΜΟΓΗ

Στο διπλανό σύστημα:

  1. Να δείξετε ότι αν το απομακρύνουμε από την Θέση Ισορροπίας, θα εκτελέσει α.α.τ. Πόση είναι η περίοδος του;
  2. Θεωρώντας ότι την χρονική στιγμή μηδέν βρίσκεται στην θέση x = +A/2 και κινείται προς τα κάτω, να γράψετε τις εξισώσεις της απομάκρυνσης, της ταχύτητας και της επιτάχυνσης συναρτήσει του χρόνου. (Θετική φορά προς τα κάτω)
  3. Να παραστήσετε γραφικά την συνισταμένη δύναμη που δέχεται το βαρίδι, σε συνάρτηση     i) με την απομάκρυνση x   ii) με τον χρόνο t   
  4. Ποιος είναι ο ρυθμός μεταβολής της ορμής του ταλαντωτή τις χρονικές στιγμές t1 = 0, και t2 = T/4
  5. Πόσος είναι ο ελάχιστος χρόνος που χρειάζεται για να μετακινηθεί ο ταλαντωτής από την θέση x1=A/2 στην θέση x2=0

Ενέργεια ταλάντωσης

  • Ισούται με την ενέργεια που προσφέρουμε αρχικά στο σύστημα για να αρχίσει να ταλαντώνεται

 

...Εμφανίζεται ως:

K=\frac{1}{2}\cdot{m}\cdot{\upsilon^2 }
K=12⋅m⋅υ2K=\frac{1}{2}\cdot{m}\cdot{\upsilon^2 }
  • Κινητική
  • Δυναμική ενέργεια ταλάντωσης
U=\frac{1}{2}\cdot{D}\cdot{x^2 }
U=12⋅D⋅x2U=\frac{1}{2}\cdot{D}\cdot{x^2 }
  • Το άθροισμα τους παραμένει σταθερό στην διάρκεια της αμείωτης ταλάντωσης.  
E=\color{Blue}{\frac{1}{2}\cdot{m}\cdot{\upsilon^2 }+\frac{1}{2}\cdot{D}\cdot{x^2 }} = \color{Red}{\frac{1}{2}\cdot{m}\cdot{{\upsilon_{max}}^2 }} = \color{Green}{\frac{1}{2}\cdot{D}\cdot{A^2 }}
E=12⋅m⋅υ2+12⋅D⋅x2=12⋅m⋅υmax2=12⋅D⋅A2E=\color{Blue}{\frac{1}{2}\cdot{m}\cdot{\upsilon^2 }+\frac{1}{2}\cdot{D}\cdot{x^2 }} = \color{Red}{\frac{1}{2}\cdot{m}\cdot{{\upsilon_{max}}^2 }} = \color{Green}{\frac{1}{2}\cdot{D}\cdot{A^2 }}

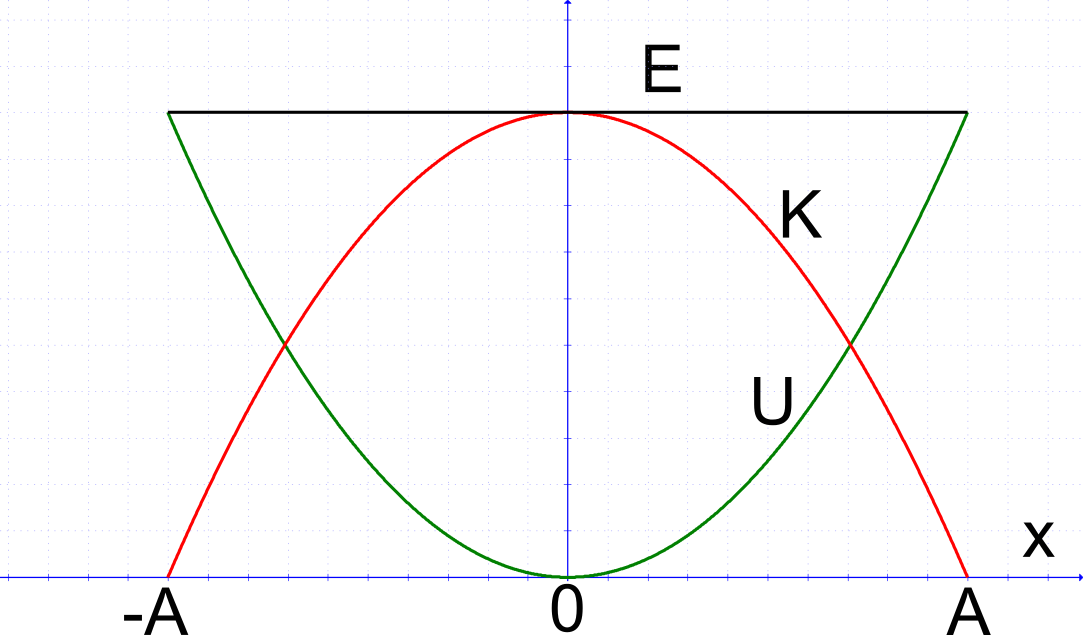
Διαγράμματα Ενέργειας Ταλαντωτή

  • Συναρτήσει απομάκρυνσης x
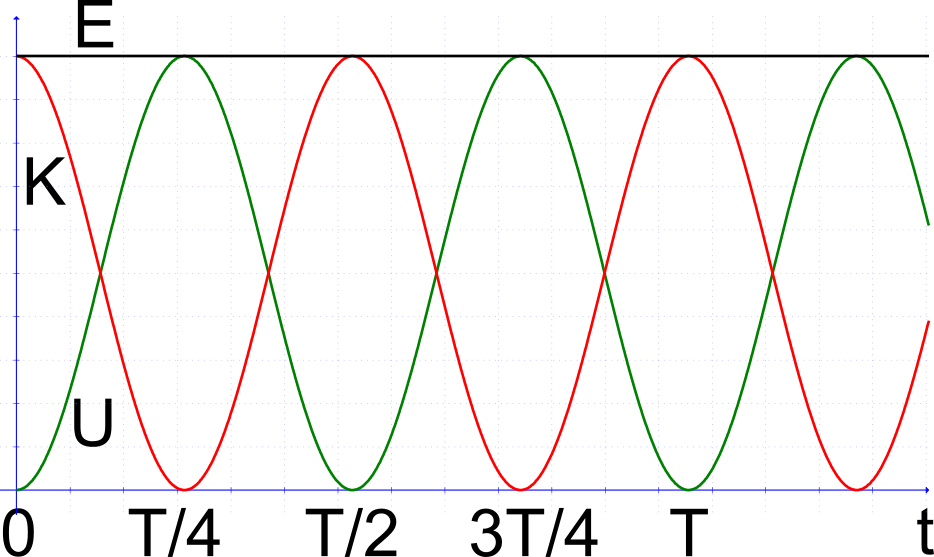
  • Συναρτήσει του χρόνου t
\color{Red}{K=E-\frac{1}{2}\cdot {D}\cdot{x^2}}
K=E−12⋅D⋅x2\color{Red}{K=E-\frac{1}{2}\cdot {D}\cdot{x^2}}
\color{green}{U=\frac{1}{2}\cdot {D}\cdot{x^2}}
U=12⋅D⋅x2\color{green}{U=\frac{1}{2}\cdot {D}\cdot{x^2}}
\color{Red}{K=E\cdot{\sigma \upsilon \nu ^2(\omega \cdot{t})}}
K=E⋅συν2(ω⋅t)\color{Red}{K=E\cdot{\sigma \upsilon \nu ^2(\omega \cdot{t})}}
\color{Green}{U=E\cdot{\eta \mu ^2(\omega \cdot{t})}}
U=E⋅ημ2(ω⋅t)\color{Green}{U=E\cdot{\eta \mu ^2(\omega \cdot{t})}}

ΕΦΑΡΜΟΓΗ

Ένα μικρό σώμα μάζας m=0,5kg βρίσκεται αρχικά ακίνητο, κρεμασμένο στο άκρο κατακόρυφου ιδανικού ελατηρίου.

Του προσφέρουμε ενέργεια Ε =16J ώστε να αρχίσει να εκτελεί α.α.τ συχνότητας f = 2Hz:

  1. Υπολογίστε την σταθερά του ελατηρίου καθώς και το πλάτος της ταλάντωσης.
  2. Πόση είναι η μέγιστη τιμή της ταχύτητας ταλάντωσης;
  3. Υπολογίστε το μέτρο της ταχύτητας του ταλαντωτή την στιγμή που αυτός βρίσκεται στην θέση x1 = A/2
  4. Ποιος είναι ο ρυθμός μεταβολής της κινητικής του ενέργειας, στην θέση x1 = A/2 
  5. Σε ποιες θέσεις η κινητική και η δυναμική ενέργεια του ταλαντωτή γίνονται ίσες;
  6. Να παραστήσετε γραφικά την δυναμική, την κινητική και την ολική του ενέργεια, σε συνάρτηση με την απομάκρυνσης x.
  7. Να παραστήσετε γραφικά την δυναμική, την κινητική και την ολική του ενέργεια, σε συνάρτηση με τον χρόνο. (Θεωρείστε ότι την t0 =0, ο ταλαντωτής βρίσκεται στην θέση ισορροπίας του και κινείται με θετική ταχύτητα)