Στάσιμα κύματα

Δημιουργία

  • Κύματα ίδιου πλάτους και συχνότητας που διαδίδονται σε αντίθετες κατευθύνσεις
y_{1}=A\cdot\eta \mu 2\pi ({t\over T} - {x \over \lambda})
y1=A⋅ημ2π(tT−xλ)y_{1}=A\cdot\eta \mu 2\pi ({t\over T} - {x \over \lambda})
y_{2}=A\cdot\eta \mu 2\pi ({t\over T} + {x \over \lambda})
y2=A⋅ημ2π(tT+xλ)y_{2}=A\cdot\eta \mu 2\pi ({t\over T} + {x \over \lambda})
  • Στα σημεία που τα δύο κύματα συμβάλλουν

 

σε συμφωνία φάσης:

 

σε αντίθεση φάσης:

 

Γενικά:   

                       

A'=2 A
A′=2AA'=2 A
A'=0
A′=0A'=0
y=\left | 2A\cdot\sigma \upsilon \nu 2\pi {x \over \lambda} \right |
y=∣2A⋅συν2πxλ∣y=\left | 2A\cdot\sigma \upsilon \nu 2\pi {x \over \lambda} \right |

(...κοιλίες)

(...δεσμοί)

προσομοίωση...

Εξίσωση

y=2A\cdot\sigma \upsilon \nu (2\pi {x \over \lambda})\cdot \eta \mu (2\pi {t\over T})
y=2A⋅συν(2πxλ)⋅ημ(2πtT)y=2A\cdot\sigma \upsilon \nu (2\pi {x \over \lambda})\cdot \eta \mu (2\pi {t\over T})

Για κύμα που το σημείο αναφοράς (x = 0)

  • είναι κοιλία
  • έχει αρχική φάση μηδέν

 

προσομοίωση...

προσομοίωση...

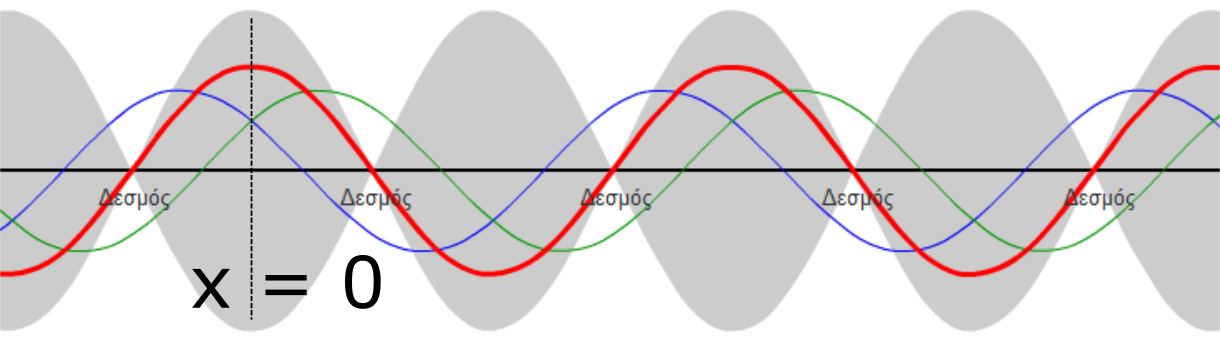
Θέσεις κοιλιών:

 

 

 

Θέσεις δεσμών

 

 

 

Μήκος Χορδής

 

όμοια άκρα:

 

ανόμοια άκρα:

 

x_\kappa =N \cdot {\lambda \over 2}
xκ=N⋅λ2x_\kappa =N \cdot {\lambda \over 2}
x_\lambda =(2N+1) \cdot {\lambda \over 2}
xλ=(2N+1)⋅λ2x_\lambda =(2N+1) \cdot {\lambda \over 2}
L =N \cdot {\lambda \over 2}
L=N⋅λ2L =N \cdot {\lambda \over 2}
L =(2N+1) \cdot {\lambda \over 4}
L=(2N+1)⋅λ4L =(2N+1) \cdot {\lambda \over 4}

Παρατηρήσεις

Δεν διαδίδεται ορμή και ενέργεια

 

Τα σημεία έχουν διαφορετικό

  • πλάτος ταλάντωσης
  • μέγιστη ταχύτητα ταλάντωσης
  • ενέργεια ταλάντωσης

 

 

Οι φάσεις διαφέρουν μεταξύ τους κατά

  • 0
  • π