Assumptions of regression

PSY 716

Assumptions of regression

Residuals are:

normally distributed
homoscedastic
independent of one another
uncorrelated with predictors

Predictors are not too multicollinear

The relationship between the predictors and outcomes is linear

Assumptions about residuals

$$ Residual = Y - \hat{Y} $$

$$\hat{Y} = b_0 + \sum_{p=1}^{P}{B_pX_p}$$

A lot of what we think of as assumptions about the outcome are assumptions about residuals.

Normally distributed residuals

We assume residuals follow a multivariate normal distribution. While this is exactly what it sounds like, it also has ramifications that are somewhat wider reaching.

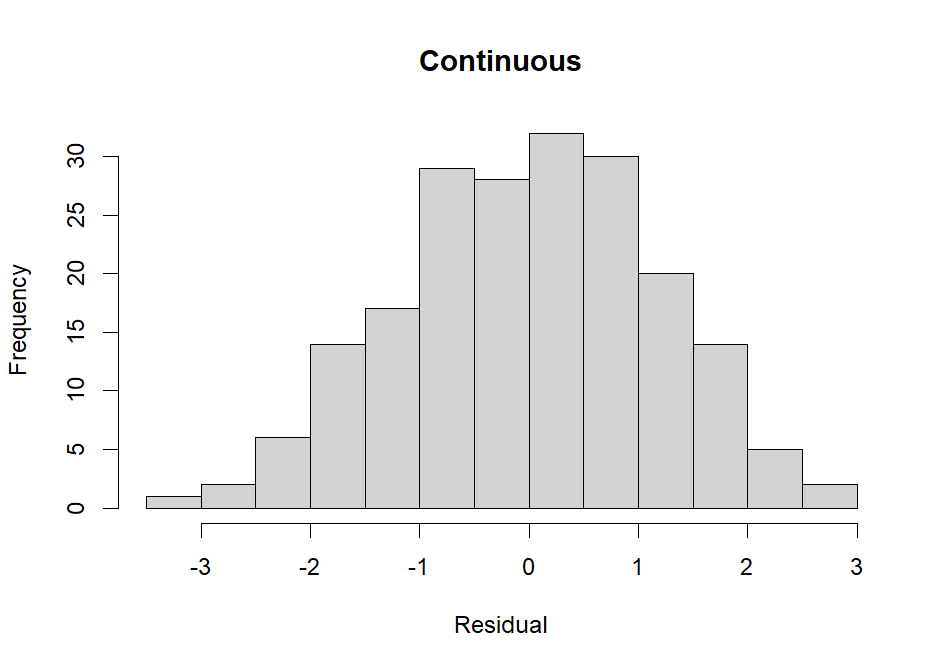
Normally distributed residuals

Specifically, if outcome, conditional on the predictors, is not able to be approximated using a normal distribution, our residuals will be non-normal. This means that ordinal or binary outcomes will often violate this assumption.

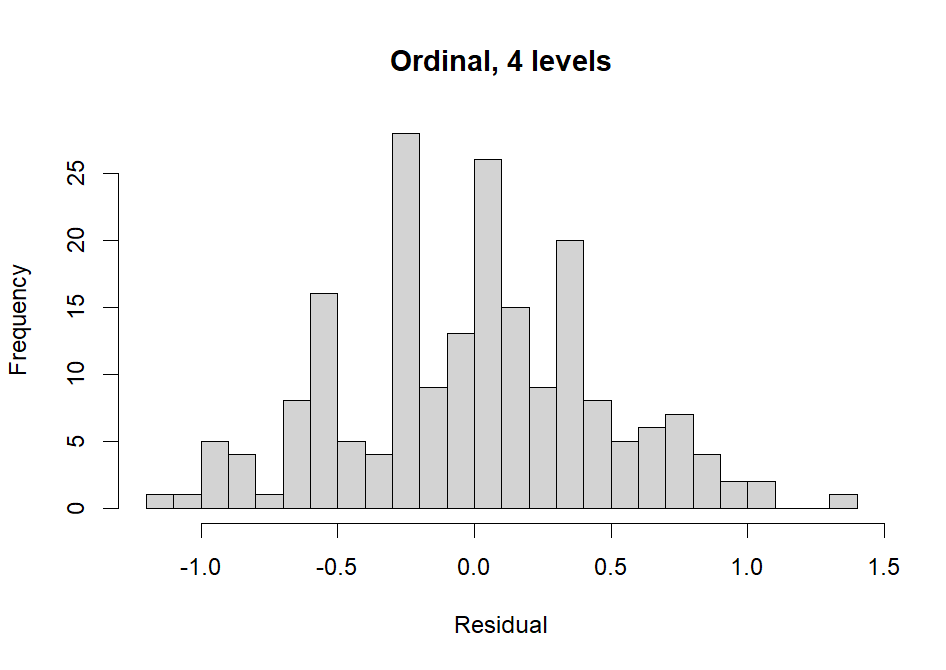
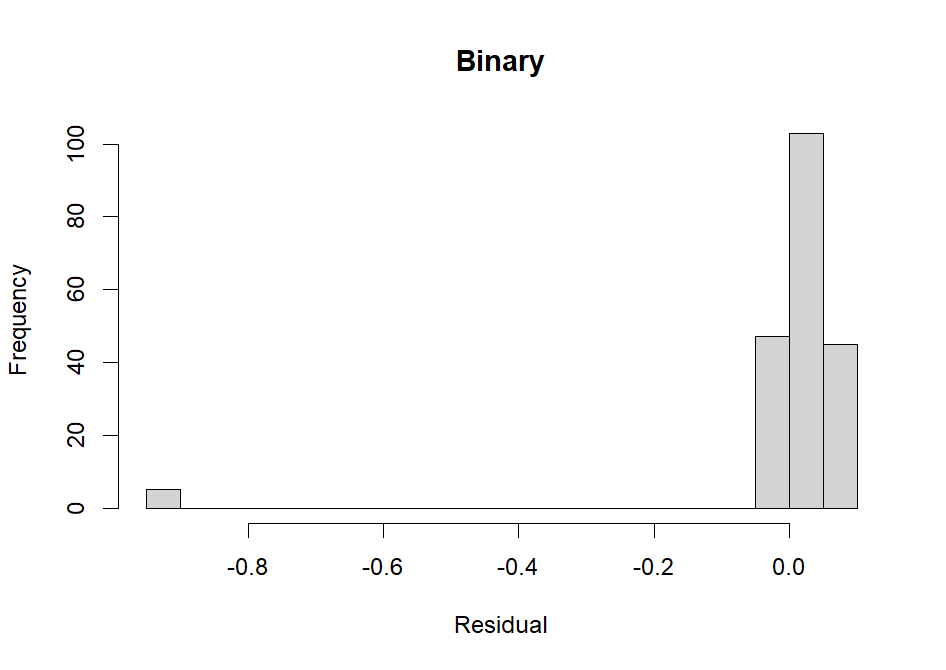
Normally distributed residuals

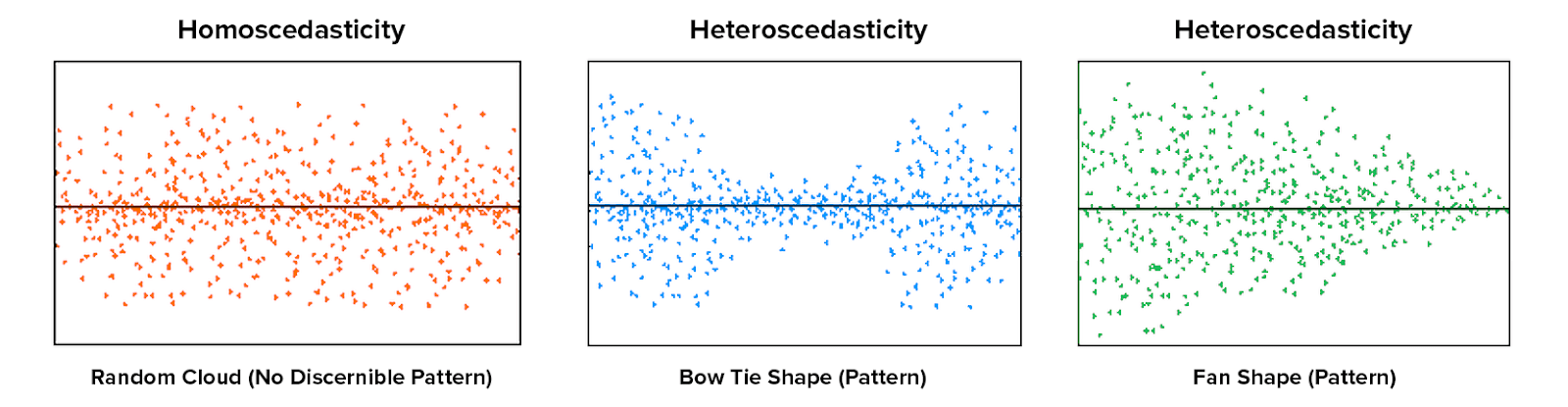
Homoscedastic residuals

This means that errors are equally distributed across levels of the outcome and the predictors.

Independence of residuals

We assume that each individual subject's residual is unrelated to each other individual subject's residual.
This assumption will be violated if subjects are clustered according to any higher-order unit.
- For instance, kids measured within the same school
- Or times measured within the same person
Fortunately, we have a set of models for this: multilevel models.

Residuals and predictors

We assume that the correlation between the residuals and our predictors is zero.
This assumption can be violated if we have an omitted variable that is related to both the predictor and outcome.

Suppose the true model would be estimated as:

$$ Y = b_0 + b_1X_1 + b_2X_2 + Error $$

But we omit X_2 from our model, so we estimate:

$$ Y = b_0 + b_1X_1 + Error $$

In the model we actually fit, our error term contains variance from $ X_2 $. If $ X_2 $ is correlated with $ X_1 $, we have violated this assumption.

Consequences of violating assumptions about residuals

Any of these assumptions being violated leads to biased standard errors, which we know means our t and F tests will be biased.
Greater vulnerability when sample size is smaller
- At larger sample sizes, non-normality can be less of a problem
Errors being correlated with predictors tends to be the most severe.
- Biased coefficients and standard errors
- Tends to signal a problem with our hypothesized model
  - i.e., that we left something out, or that causal relationships are reversed.

Multicollinearity

Multicollinearity refers to the case of predictors being highly correlated with one another.
We know that this poses problems for inference due to there being very little non-overlapping variance.
They will also cause...
- Coefficients to change in magnitude (sometimes even direction)
- Standard errors to be inflated
- Why? Look at the formulas for these!

Multicollinearity

How do we determine whether there is multicollinearity?
We could just look at the correlations among the variables.
A more targeted way to look at this is the variance inflation factor (VIF), which is calculated as follows:

$$ VIF_p = \frac{1}{1 - R_p^2} $$

where $ R_p^2 $ is the multiple correlation from a model predicting $ X_p $ with every variable in the model except $ X_p $.

The relationship between the predictors and outcome is linear.

In linear regression, we assume that the predictors linearly increment the predicted outcome.
If we are wrong...
- We will often see it in our residuals (making this related to the other assumptions)
- We can fit a nonlinear model! Two types of nonlinear models
  - Generalized linear model
  - Linear model with polynomial terms -- e.g.,

$$ Y = b_0 + b_1X_1 + b_2X_1^2 + b_3X_1^3 + Error $$