Multilevel modeling, part 1

PSY 356

  • Introduction: What are multilevel models and why would we use them?
  • Between vs. within-group variance
    • ​Fixed vs. random effects
    • Intra-class correlation
    • Our first multilevel model: the random-effects ANOVA 
  • Incorporating predictors
    • ​Random intercept regression model
    • Intercepts-as-outcomes
    • Slopes-as-outcomes

Multilevel models

Motivation: nested data

  • We use multilevel models in the presence of a nested data structure.
    • Multiple students in the same school
    • Multiple children of the same mother
    • Multiple time points observed on the same person

 

Why use multilevel models?

  • In the presence of nested data, the assumption of independence of errors is not met.

  • Multilevel models allow us to...

    • ...model group-level effects, if they are of substantive interest

    • ...determine the relative magnitude of within-group effects

    • ...generalize to a population of group effects

 

Independence of Error Terms

  • In the presence of nested data, the assumption of independence of errors is not met.

  • This is key, because a standard linear model assumes that between-group differences are the only source of variation

  • If we ignore nesting of data, we obtain biased estimates of coefficients and standard errors

    • Standard errors often downwardly biased, leading to inflated Type I error rate

Other options

  • Randomly sample one observation from each group

  • Fixed effects model

    • i.e., including a regression coefficient for each grouping

  • Two approaches which only estimate marginal effects

    • Generalized estimating equations

    • Adjustments to standard errors which adjust for clustering

      • Huber-White SEs, so-called "sandwich" estimator

Why use multilevel models?

  • Multilevel models allow us to...

    • ...model group-level effects, if they are of substantive interest

      • e.g., How does school climate affect math scale scores?

    • ...determine the relative magnitude of within-group effects

      • e.g., How much do school-level factors affect math scale scores, relative to child-level scale scores?

    • ...generalize to a population of group effects

      • e.g., How much do school-level factors affect math scale scores, relative to child-level scale scores, above and beyond the schools we are currently considering?

Why use multilevel models?

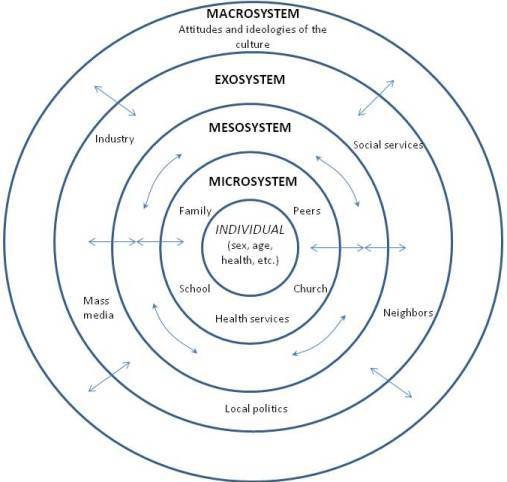
Multilevel models, at least theoretically, allow us to model the interplay between these levels.

A note on nomenclature

  • Multilevel models go by a number of different names:
    • Random coefficient models
    • Mixed models
    • Hierarchical linear models
  • Additionally, the same model is often referred to in multiple different ways
    • e.g., a slopes-as-outcomes model vs. a model with a cross-level interaction
    • We will try to be as general as possible but if ever you are confused, please just ask!

Between-groups variance vs. within-groups variance

Partitioning variance

  • Our first task is to figure out how much variance in our outcome is related to differences between groups, and how much is related to variation within groups.
    • How similar are kids who go to the same school in terms of math ability?
    • How similar are a teenager's self-reported depressive symptoms from one day to the next?
    • How similar are externalizing problems among children of the same parent?

Motivating example: ECLS-K

  • Nationally representative study children's cognitive and social development from kindergarten to eighth grade

  • \(N=15305\) children sampled starting in 1998

  • Here we look at math skills in a cross-section of students in third grade

  • Children nested within school

Motivating example: ECLS-K

  • Questions we wish to answer

    • To what extent do differences between children in math ability owe to differences between schools?

    • Which child-level factors are associated with higher math scores?

    • Which school-level factors are associated with higher math scores?

    • Do the effects of child-level factors vary from one school to the next?

MathScore_{ij} = \beta_{0j} + r_{ij}
\beta_{0j} = \gamma_{00} + u_{0j}

The random-effects ANOVA model

Level 1

Level 2

where \(i\) indexes children and \(j\) indexes school.

r_{ij}\sim N\left(0,\sigma^2\right)
u_{0j}\sim N\left(0,\tau_{00}\right)
MathScore_{ij} = \beta_{0j} + r_{ij}
\beta_{0j} = \gamma_{00} + u_{0j}

\(\beta_{0j}\) is a subject's predicted math score, given that they are a student at school \(j\).

Within-group variance

Level 1

Level 2

r_{ij}\sim N\left(0,\sigma^2\right)
u_{0j}\sim N\left(0,\tau_{00}\right)

\(r_{ij}\) is the subject-specific deviation from this predicted mean.

\(\sigma^2\) is the within-school variance.

MathScore_{ij} = \beta_{0j} + r_{ij}
\beta_{0j} = \gamma_{00} + u_{0j}

\(\gamma_{00}\) is the grand mean math score across schools.

Between-group variance

Level 1

Level 2

r_{ij}\sim N\left(0,\sigma^2\right)
u_{0j}\sim N\left(0,\tau_{00}\right)

\(u_{0j}\) is the school-specific deviation from this grand mean.

\(\tau_{00}\) is the between-school variance.

MathScore_{ij} = \gamma_{00} + u_{0j} + r_{ij}

grand mean across schools

Putting it together

Reduced form equation

r_{ij}\sim N\left(0,\sigma^2\right)
u_{0j}\sim N\left(0,\tau_{00}\right)

some school-specific deviation from that grand mean

some child-specific deviation from the school-implied value

Total variance =  \(\tau_{00}\) +\(\sigma^2\)

How much of the variance in math scores owes to differences between schools?

  • We answer this question with an intraclass correlation coefficient (ICC).

\(ICC = \frac{BetweenGroups Variance}{Total Variance}\)

\(ICC = \frac{\tau_{00}}{\tau_{00}+\sigma^2}\)

Incorporating predictors

Motivating example: ECLS-K

  • Questions we wish to answer

    • To what extent do differences between children in math ability owe to differences between schools?

    • Which child-level factors are associated with higher math scores?

    • Which school-level factors are associated with higher math scores?

    • Do the effects of child-level factors vary from one school to the next?

MathScore_{ij} = \beta_{0j} + \beta_{1j}HoursTV_{ij} + r_{ij}
\beta_{0j} = \gamma_{00} + u_{0j}

\(\beta_{0j}\) is the predicted math score for a child who watches no TV, given that they are a student at school \(j\).

Random intercept model

Level 1

Level 2

r_{ij}\sim N\left(0,\sigma^2\right)
u_{0j}\sim N\left(0,\tau_{00}\right)
\beta_{1j} = \gamma_{10}

\(\beta_{1j}\) is the effect of hours of TV watched on math score for school \(j\). Note that it is the same for all schools here.

MathScore_{ij} = \beta_{0j} + r_{ij}
\beta_{0j} = \gamma_{00} + u_{0j}

The random-effects ANOVA model

Level 1

Level 2

where \(i\) indexes children and \(j\) indexes school.

r_{ij}\sim N\left(0,\sigma^2\right)
u_{0j}\sim N\left(0,\tau_{00}\right)
MathScore_{ij} = \gamma_{00} + \gamma_{10}HoursTV_i + u_{0j} + r_{ij}

Random intercept model

Reduced-form equation

r_{ij}\sim N\left(0,\sigma^2\right)
u_{0j}\sim N\left(0,\tau_{00}\right)

random

fixed

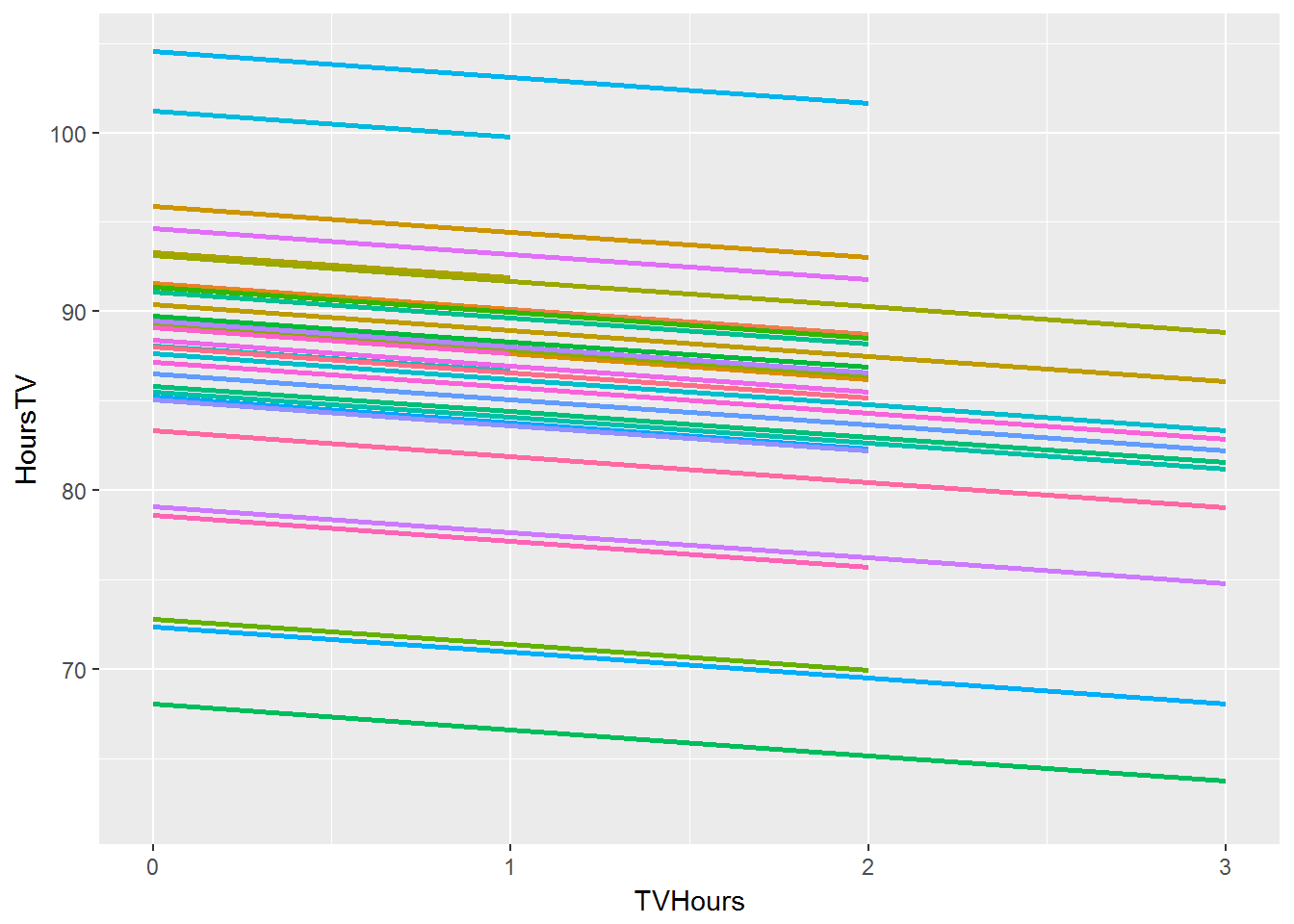
MathScore_{ij} = \gamma_{00} + \gamma_{10}HoursTV_{ij} + u_{0j} + r_{ij}

Random intercept model

r_{ij}\sim N\left(0,\sigma^2\right)
u_{0j}\sim N\left(0,\tau_{00}\right)

random

fixed

Note that this model could also be run (erroneously) as a standard linear regression by getting rid of random effects!

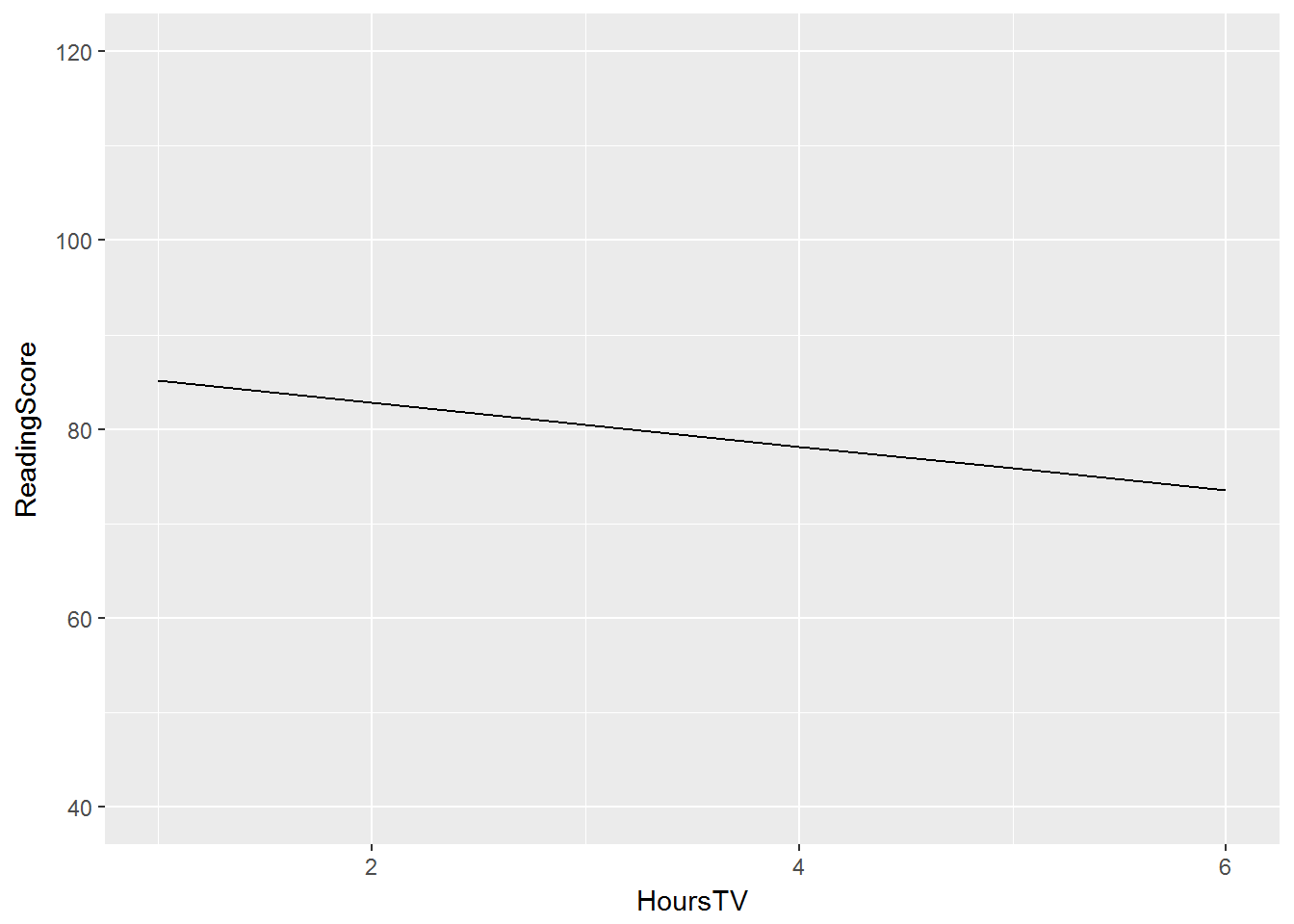
Example: ECLS-K

  • We predict math scale score from the number of hours of TV watched after dinner without accounting for nesting within schools

  • We find a fairly precipitous drop, predicting a 2.32-point reduction in math score for each hour of TV watched.

Motivating example: ECLS-K

  • Questions we wish to answer

    • To what extent do differences between children in math ability owe to differences between schools?

    • Which child-level factors are associated with higher math scores?

    • Which school-level factors are associated with higher math scores?

    • Do the effects of child-level factors vary from one school to the next?

MathScore_{ij} = \beta_{0j} + \beta_{1j}HoursTV_{ij} + r_{ij}
\beta_{0j} = \gamma_{00} + \gamma_{01}PctFRL_j + u_{0j}

Intercepts-as-outcomes model

Level 1

Level 2

r_{ij}\sim N\left(0,\sigma^2\right)
u_{0j}\sim N\left(0,\tau_{00}\right)
\beta_{1j} = \gamma_{10}

Here \(\gamma_{01}\) conveys the effect of \(PctFRL_j\) (the percentage of students qualifying for free or reduced lunch at school \(j\)) on the overall predicted math score for school \(j\).

MathScore_{ij} = \beta_{0j} + \beta_{1j}HoursTV_i + r_{ij}
\beta_{0j} = \gamma_{00} + u_{0j}

\(\beta_{0j}\) is the predicted math score for a child who watches no TV, given that they are a student at school \(j\).

Random intercept model

Level 1

Level 2

r_{ij}\sim N\left(0,\sigma^2\right)
u_{0j}\sim N\left(0,\tau_{00}\right)
\beta_{1j} = \gamma_{10}

\(\beta_{1j}\) is the effect of hours of TV watched on math score for school \(j\). Note that it is the same for all schools here.

MathScore_{ij} = \gamma_{00} + \gamma_{01}PctFRL_j + \gamma_{10}HoursTV_{ij} +

Intercepts-as-outcomes model

Reduced-form equation

r_{ij}\sim N\left(0,\sigma^2\right)
u_{0j}\sim N\left(0,\tau_{00}\right)

random

fixed

u_{0j} + r_{ij}

Note that even though \(PctFRL_j\) is a school-level variable and \(HoursTV_i\) is a child-level variable, both are fixed effects. 

Motivating example: ECLS-K

  • Questions we wish to answer

    • To what extent do differences between children in math ability owe to differences between schools?

    • Which child-level factors are associated with higher math scores?

    • Which school-level factors are associated with higher math scores?

    • Do the effects of child-level factors vary from one school to the next?

MathScore_{ij} = \beta_{0j} + \beta_{1j}HoursTV_{ij} + r_{ij}
\beta_{0j} = \gamma_{00} + \gamma_{01}PctFRL_j + u_{0j}

Slopes-as-outcomes model

Level 1

Level 2

r_{ij}\sim N\left(0,\sigma^2\right)
\begin{bmatrix} u_{0j} \\ u_{1j} \end{bmatrix} \sim N \begin{bmatrix} \tau_{00} & \\ \tau_{01} & \tau_{11} \end{bmatrix}
\beta_{1j} = \gamma_{10} + \gamma_{11}PctFRL_j + u_{1j}

Here \(\gamma_{01}\) conveys the effect of \(PctFRL_j\) (the percentage of students qualifying for free or reduced lunch at school \(j\)) on the overall predicted math score for school \(j\), and \(\gamma_{01}\) conveys the effect of \(PctFRL_j\) on the effect of \(HoursTV_i\).

MathScore_{ij} = \beta_{0j} + \beta_{1j}HoursTV_{ij} + r_{ij}
\beta_{0j} = \gamma_{00} + \gamma_{01}PctFRL_j + u_{0j}

Intercepts-as-outcomes model

Level 1

Level 2

r_{ij}\sim N\left(0,\sigma^2\right)
u_{0j}\sim N\left(0,\tau_{00}\right)
\beta_{1j} = \gamma_{10}

Here \(\gamma_{01}\) conveys the effect of \(PctFRL_j\) (the percentage of students qualifying for free or reduced lunch at school \(j\)) on the overall predicted math score for school \(j\).

MathScore_{ij} = \gamma_{00} + \gamma_{01}PctFRL_j +

Slopes-as-outcomes model

Reduced-form equation

random

fixed

u_{0j} + u_{1j}HoursTV_{ij} + r_{ij}
\left(\gamma_{10} + \gamma_{11}PctFRL_j\right)HoursTV_{ij} +

fixed

\begin{bmatrix} u_{0j} \\ u_{1j} \end{bmatrix} \sim N \begin{bmatrix} \tau_{00} & \\ \tau_{01} & \tau_{11} \end{bmatrix}
r_{ij}\sim N\left(0,\sigma^2\right)

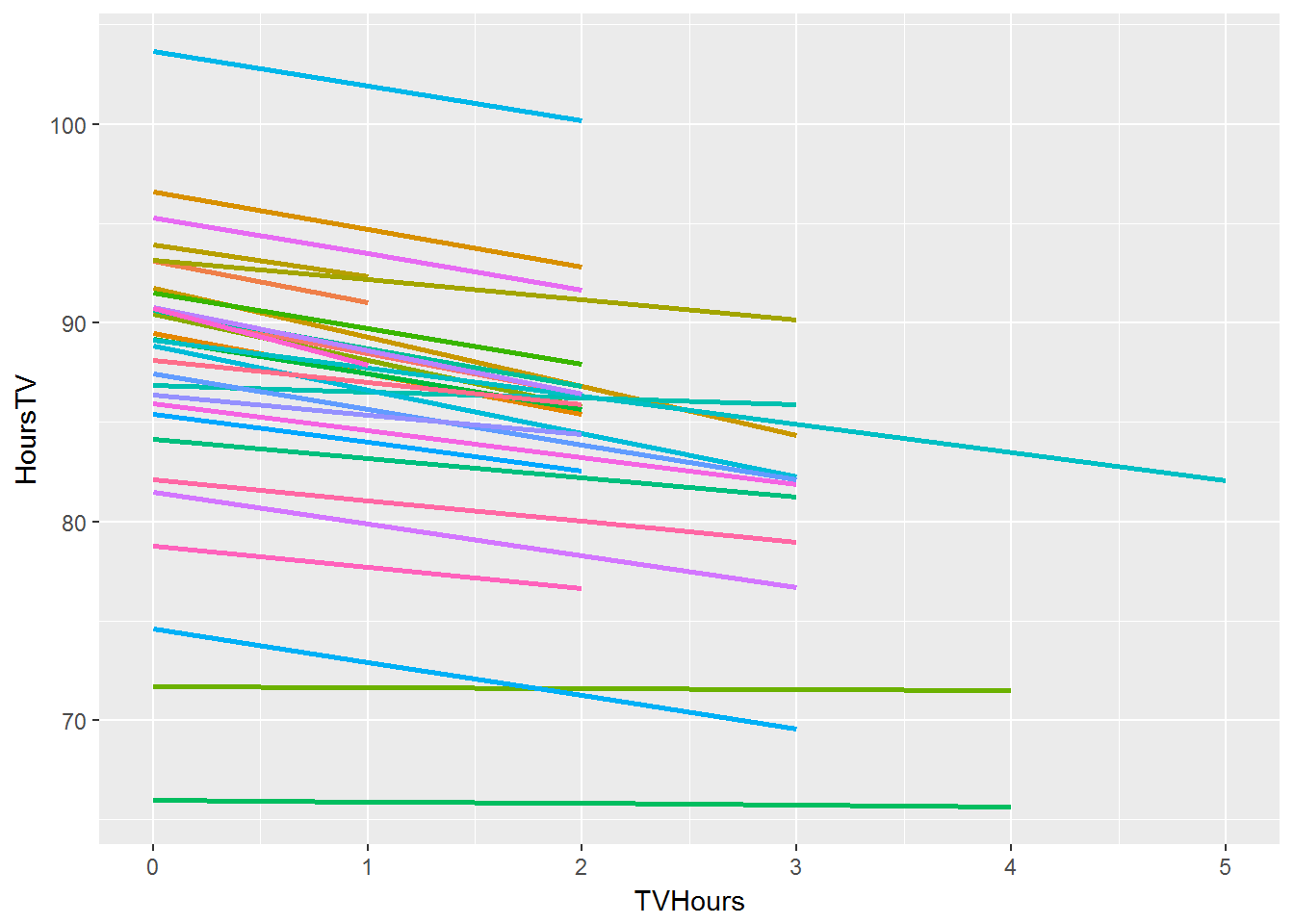
Assessing the significance of effects

  • Notice that we have not been examining significance tests for fixed effects.
    • This makes it hard to say, e.g., whether the effect of a level-2 variable on the level-1 slope is significant
  • Our best strategy is to use likelihood ratio tests
    • ​Our MO: Test whether the fit of Model A, which contains all of the relevant effects, is significantly better than Model B, which contains a subset of these effects.
    • We say that Model B is "nested" within Model A, but note that the word means something different here.