Multilevel Modeling, Part 2

PSY 356

Multilevel models for longitudinal data

Nationally representative survey of $N=6504$ adolescents
Each followed up for a maximum of five time points
Ages at the first time point ranged from 13 to 21.
Ages at the fifth time point ranged from 35 to 42.
We are using data from the first four time points.
Here, we predict drinking score, a composite score of three drinking-related indicators, from adolescence through early adulthood.

Motivating Example: Add Health

Drinking_{ij} = \beta_{0j} + \beta_{1j}Age_{ij} + r_{ij}

\beta_{0j} = \gamma_{00} + u_{0j}

\beta_{1j} = \gamma_{10}

u_{0j}\sim N\left(0,\tau_{00}\right)

r_{ij}\sim N\left(0,\sigma^2\right)

Level 2

Level 1

Random-intercept model

Here, $Age_{ij}$ and $Drinking_{ij}$ are the age and drinking score, respectively, of subject $j$ at time $i$, and Note that under this formulation, only the intercept can vary by person.

Drinking_{ij} = \beta_{0j} + \beta_{1j}Age_{ij} + r_{ij}

\beta_{0j} = \gamma_{00} + u_{0j}

\beta_{1j} = \gamma_{10} + u_{1j}

\begin{bmatrix} u_{0j} \\ u_{1j} \end{bmatrix} \sim N \begin{bmatrix} \tau_{00} & \\ \tau_{01} & \tau_{11} \end{bmatrix}

r_{ij}\sim N\left(0,\sigma^2\right)

Level 2

Level 1

Random-slopes model

Now, under this formulation, we can have variation in the slopes by person.

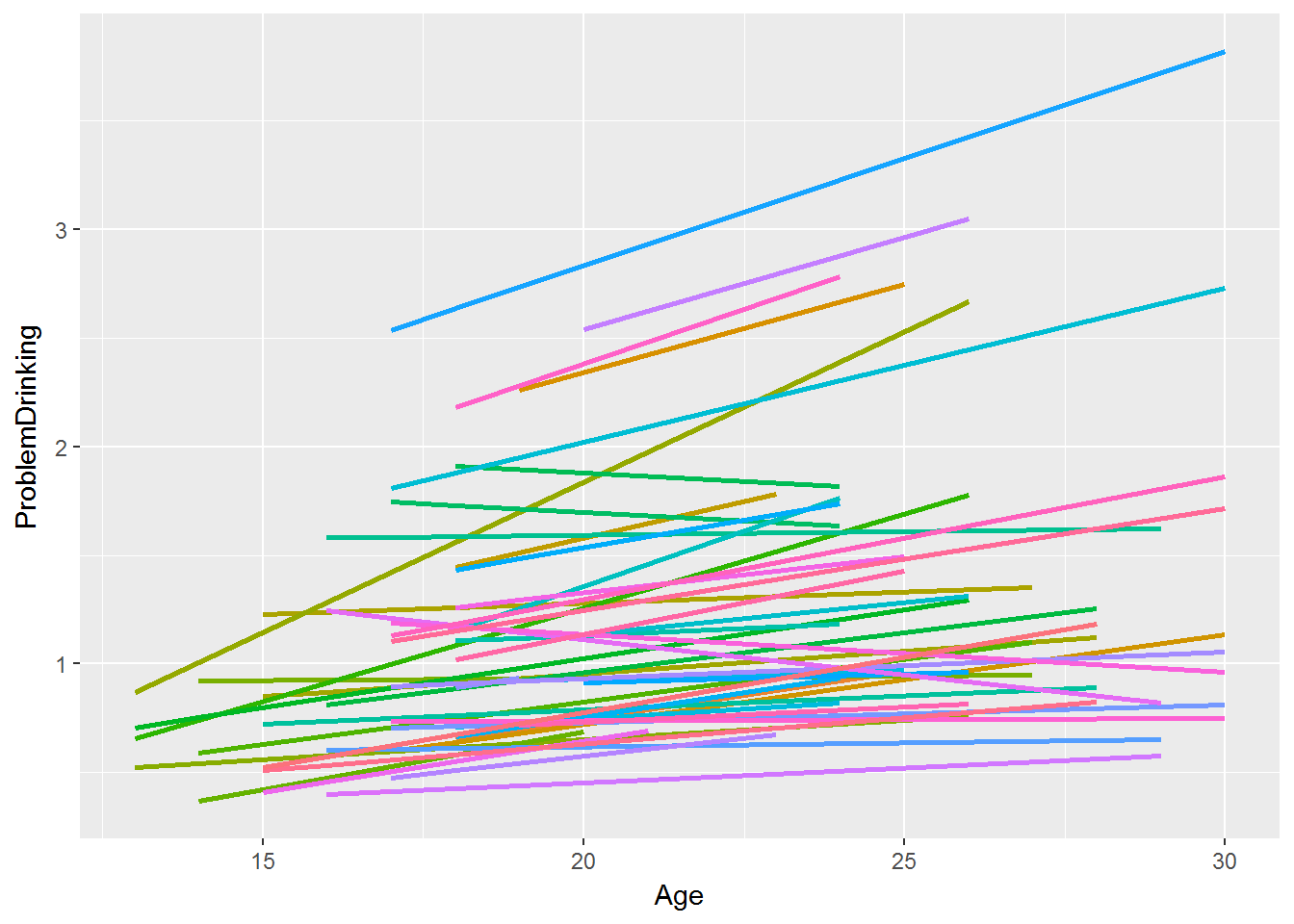
For linear growth, we can just put age in there, or we can alter it any number of ways:
- We can subtract out the first time
- We can rescale it by some multiple (e.g., 10)
  - Sometimes this helps with convergence
We can also enter a quadratic component of time - i.e., $age^2$.
- Or cubic ($age^3$), quartic ($age^4$), not sure if quintic ($age^5$) is a word but let's go with it...
Note that if you enter in a polynomial, you must include all lower-order polynomials.

How does time enter the model?

Drinking_{ij} = \beta_{0j} + \beta_{1j}Age_{ij} + \beta_{2j}Age^2_{ij} + r_{ij}

\beta_{0j} = \gamma_{00} + u_{0j}

\beta_{1j} = \gamma_{10} + u_{1j}

\begin{bmatrix} u_{0j} \\ u_{1j} \end{bmatrix} \sim N \begin{bmatrix} \tau_{00} & \\ \tau_{01} & \tau_{11} \end{bmatrix}

r_{ij}\sim N\left(0,\sigma^2\right)

Level 2

Level 1

Adding a quadratic component

This can help us to model change that increases and subsequently decreases or levels off. Note that we could include a random effect for that quadratic component too.

\beta_{2j} = \gamma_{20}

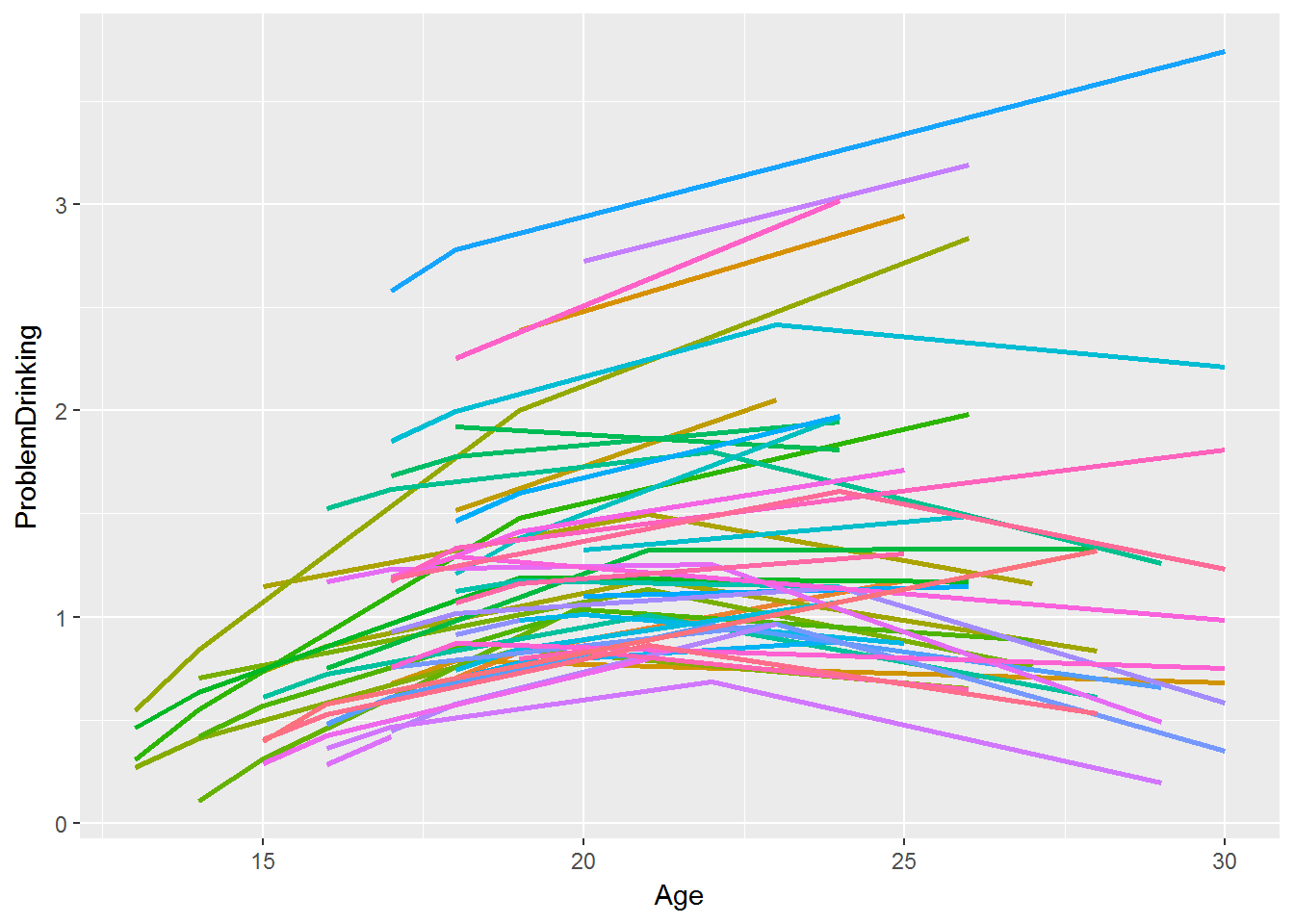
Level 2: We can add person-level predictors by allowing the intercept, slope, or both to vary for different people.
- Again, this is the same as the intercepts-as-outcomes and slopes-as-outcomes model, but don't worry too much about the terminology.
Level 1: We can add a time-level predictor, but note that the interpretation of these coefficients can be challenging.
- If a variable is contemporaneous with the outcome, it can be challenging to make causal statements.

Predictors

Drinking_{ij} = \beta_{0j} + \beta_{1j}Age_{ij} + r_{ij}

\beta_{0j} = \gamma_{00} + \gamma_{01}Male_j + u_{0j}

\beta_{1j} = \gamma_{10} + u_{1j}

\begin{bmatrix} u_{0j} \\ u_{1j} \end{bmatrix} \sim N \begin{bmatrix} \tau_{00} & \\ \tau_{01} & \tau_{11} \end{bmatrix}

r_{ij}\sim N\left(0,\sigma^2\right)

Level 2

Level 1

Adding predictors

Now we have the intercept of drinking being allowed to differ between males and females. We could also allow the slopes to differ.

Special cases

The paired samples t-test examines the difference between paired observations:

$$t = \frac{\bar{d}}{\frac{s_d}{\sqrt{n}}}$$

Where:

$d_i = y_{i1} - y_{i0}$ (difference between paired observations)
$\bar{d}$ is the mean of differences
$s_d$ is the standard deviation of differences
$n$ is the number of pairs

Paired-samples t-tests as MLM's

We can reframe this as a multilevel model, with measurements nested within subjects:

Level 1

where:

$y_{ij}$ is the outcome for subject $j$ at measurement $i$
$G_{ij}$ is the dummy-coded group variable (0 = condition 0, 1 = condition 1)
$r_{ij}$ is the measurement-level residual
$\gamma_{00}$ is the average outcome in condition 0
$\gamma_{10}$ is the average difference between conditions
$u_{0j}$ are subject-level random effects

$$\beta_{0j} = \gamma_{00} + u_{0j}$$

$$y_{ij} = \beta_{0j} + \beta_{1j}G_{ij} + r_{ij}$$

Level 2

$$\beta_{1j} = \gamma_{10}$$

$\gamma_{10}$ is equivalent to $\bar{d}$ in the paired t-test
Testing $H_0: \gamma_{10} = 0$ is equivalent to the paired t-test
Critical note: standard paired-samples t-test does NOT include random slope
The multilevel approach allows for:
- Missing data
- Inclusion of covariates
- More complex variance structures

Interpretation

Repeated measures ANOVA examines differences across multiple conditions within subjects:

$$ F = \frac{MS_{group}}{MS_{error}} = \frac{\frac{SS_{group}}{df_{group}}}{\frac{SS_{error}}{df_{error}}} $$

where:

$ SS_{group} $ is the sum of squares for group effect
$ SS_{error} $ is the sum of squares for error
$ df_{group} = k - 1 $ ($ k $ is the number of conditions)
$ df_{error} = (N-1)(k-1) $ (N is the number of subjects)

Key assumption: Sphericity (equal variances of differences between all pairs of conditions)

Repeated-measures ANOVA's as MLM's

We can reframe this as a multilevel model with measurements nested within subjects:

$$y_{ij} = \beta_{0j} + \sum_{m=1}^{k-1} \beta_{mj}G_{mij} + r_{ij}$$

$$\beta_{0j} = \gamma_{00} + u_{0j}$$

$$\beta_{mj} = \gamma_{m0}$$

where:

$ y_{ij} $ is the outcome for subject $ j $ at measurement occasion $ i $
$ G_{mij} $ are dummy codes for conditions (reference is condition 0)
$ r_{ij} $ is the measurement-level residual with variance $ \sigma^2 $
$ \gamma_{00} $ is the average outcome in the reference condition
$ \gamma_{m0} $ represents mean differences between each condition and reference
$ u_{0j } $ are subject-level random effects with variance $ \tau^2 $

Level 1

Level 2

Testing omnibus hypothesis $ (H_0: \gamma_{10} = \gamma_{20} = ... = \gamma_{(k-1)0} = 0) $ is equivalent to repeated measures ANOVA F-test
The multilevel approach offers several advantages:
- Handles missing data appropriately
- Allows inclusion of subject-level and time-varying covariates
- Can model more complex variance structures beyond sphericity
- Permits random slopes (allowing treatment effects to vary by subject)
- Accommodates continuous predictors and more complex designs
- Can handle unbalanced designs and irregular measurement occasions

Note: The standard RM-ANOVA assumes compound symmetry and sphericity, while multilevel models can relax these assumptions by specifying different variance-covariance structures.

Interpretation

Here, we consider a single person as a "group", in the sense that all time points are nested within a given person.
We will use time as a Level-1 predictor.
The models we're going over can be considered a special case of structural equation models.
One piece of advice: don't get too hung up on which piece of MLM jargon (e.g., intercepts-as-outcomes, slopes-as-outcomes) each model maps onto.

Longitudinal data

Thank you!

colev@wfu.edu