
Mechanical Engineering, Carnegie Mellon University
Advisors: Prof. Burak Kara, Prof. Jessica Zhang

Mechanical Engineering, Carnegie Mellon University
Advisors: Prof. Burak Kara, Prof. Jessica Zhang
Motivation
ML surrogates for biomedical applications
-
Application 1
-
Application 2
-
Application 3
FLARE: Fast Low...
-
Highlights
-
What needs to be done with FLARE
- Develop time-stepper, time-conditioning mechanism for FLARE
Timeline
-
PHASE 1: Understand and test/ benchmark on simple problems
- Long Range Arena
- Steady benchmarks
- OCT - NOV
-
PHASE 2: Propose modifications for time-series calculations
- Time conditioning
- Use prefix-conditioning in Long Range Arena as precursor to time-conditioning problem
- NOV - JAN
-
PHASE 3: Test on biomedical applications
- Application 1: dataset, goals, benchmark model performance
- Application 2:
- FEB - MAY
- FLARE + Time
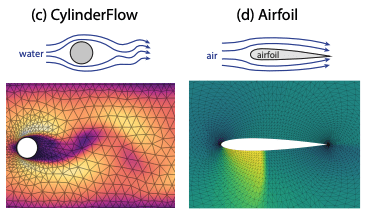
- transient calculations (LPBF, cylinder flow)
- diffusion (image generation, ...)
- Enhancements to FLARE/ Transformer
- PDE problems
- Long Range Arena problems
Update 4/02/25
Modeling dynamical deformation in LPBF with neural network surrogates
-
Contributions:
- Novel transformer architecture for spatial slicing
- Novel transformer architecture for time-series modeling
- Time-series dataset for LPBF
-
Updates:
- Testing architecture modifications on Cylinder Flow benchmar dataset
-
Next steps:
- Continue experimenting with architecture for steady state
- Continue benchmarking for rollout
Data-flow arguments
- Slicing
- Larger key, value projection
- Learned query [H, M, D]
- Transolver applies Linear projection to permuted x. Perceiver POV allows us to view the weights of the linear layer as latent query embedding. Transolver thus uses the same query vector for each head. We give each head a unique one.
-
QK normalizationNormalize query and key embeddings for stable training (ref. NGPT paper)
-
Query - head mixing
- Allow slice weights in different heads to communicate with each other (ref. Multi-Token attention, Talking-Head attention papers)
- cannot do key mixing because key vector is of size N (point cloud). can't apply any permutation-dependent conv either.
Head-wise normalizatoin - Stability, break symmetry- Self-attention
-
Permute & QKV projection [H*D, H*D]
- Transolver applies same projection to each head in parallel. No head-mixing. We allow for more head-mixing here.
- Query-head mixing above is only on the attention weights. Here, we mix token value across heads.
- Think of transolver as applying a block diagonal matrix with each block being the same as us as applying a full matrix.
-
Permute & QKV projection [H*D, H*D]
- Deslicing
Experiments - standard PDE benchmarks
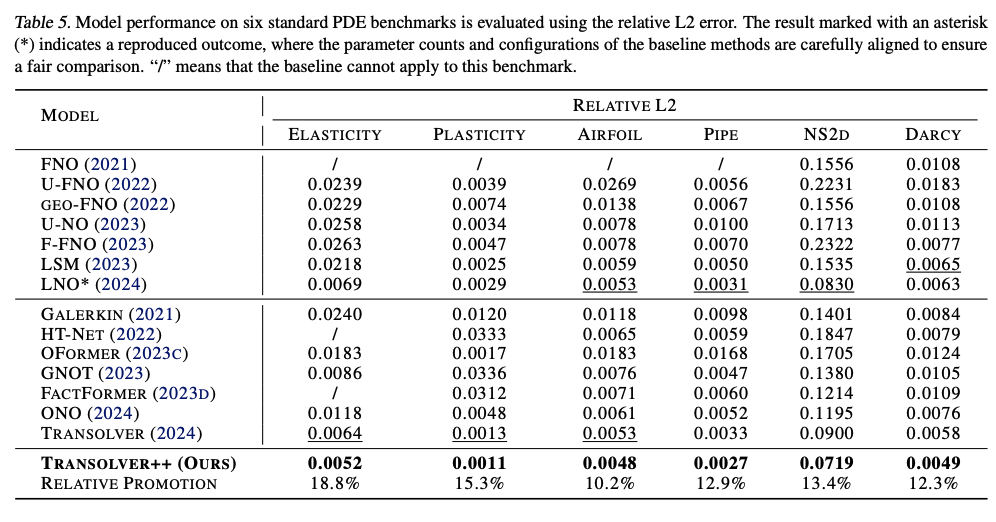
0.0153
0.0092
| ShapeNet Car |
- | |||||||
|---|---|---|---|---|---|---|---|---|
| LNO | 0.0029 | 0.0049 | 0.0026 | 0.0845 | - | - | ||
| CAT (ours) | 0.00315 | - | - | - | - | 0.00590 | 0.0637 | - |
|
Transolver w/ conv Transolver w/o conv |
/ 0.0064 |
- - |
0.0055 0.0082 |
- - |
- - |
0.00594 0.014313 |
/ 0.0760 |
/ - |

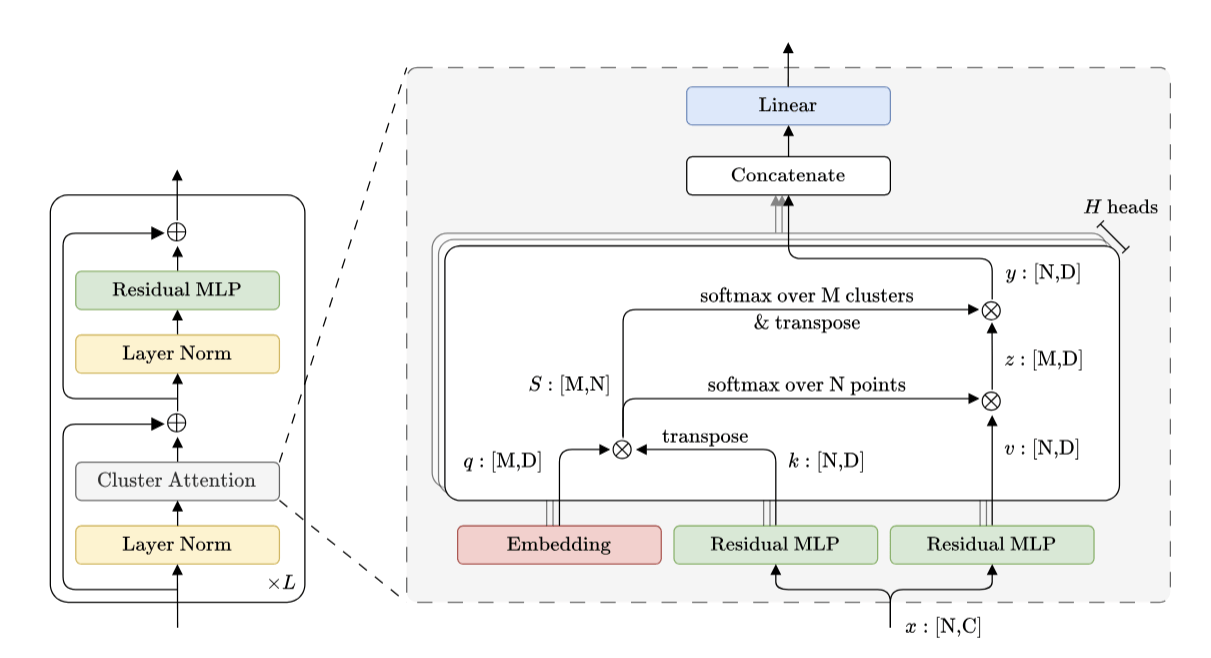
Cluster Attention Transformer
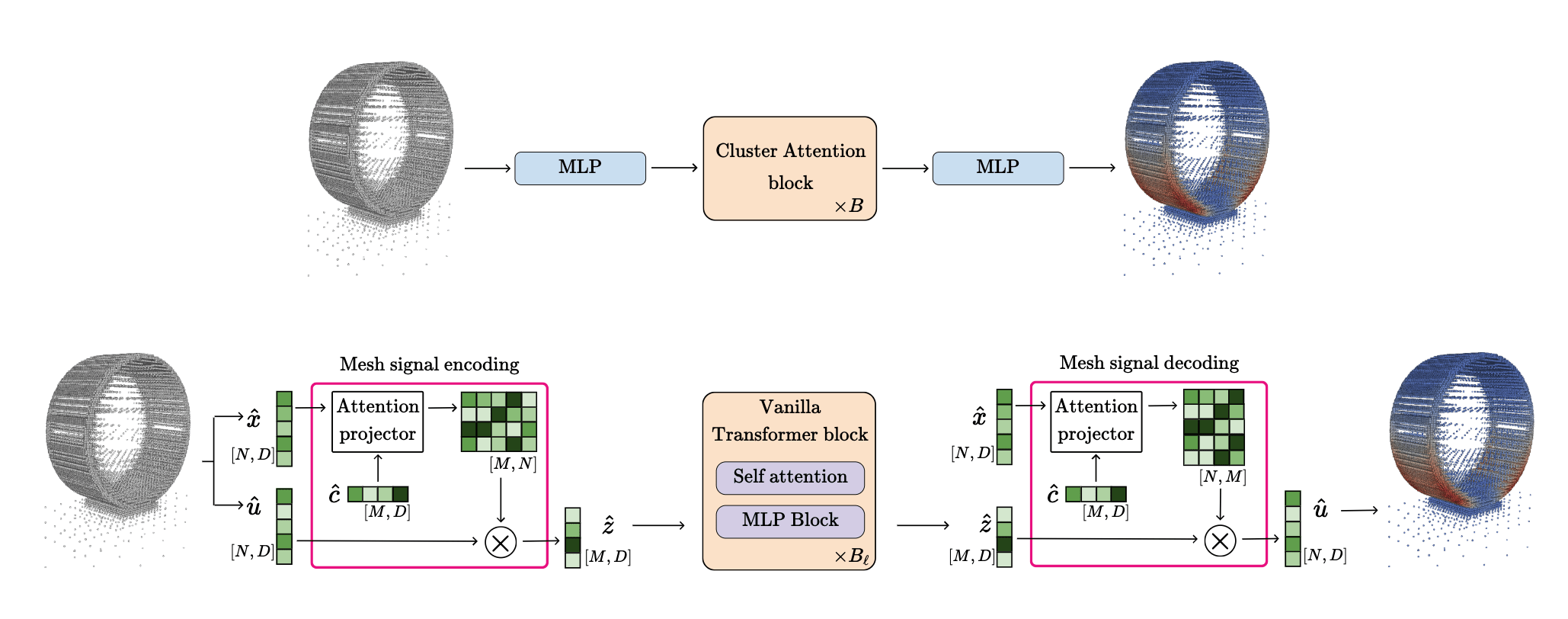
CAT Block
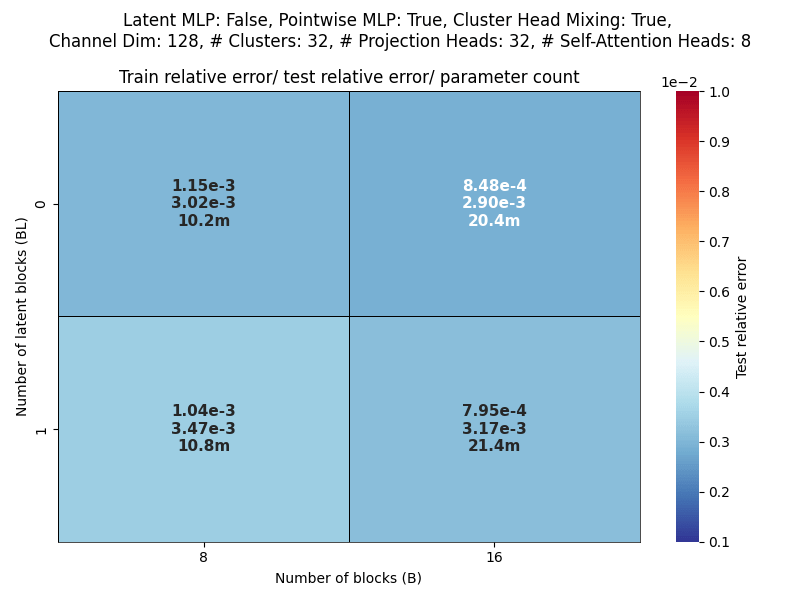
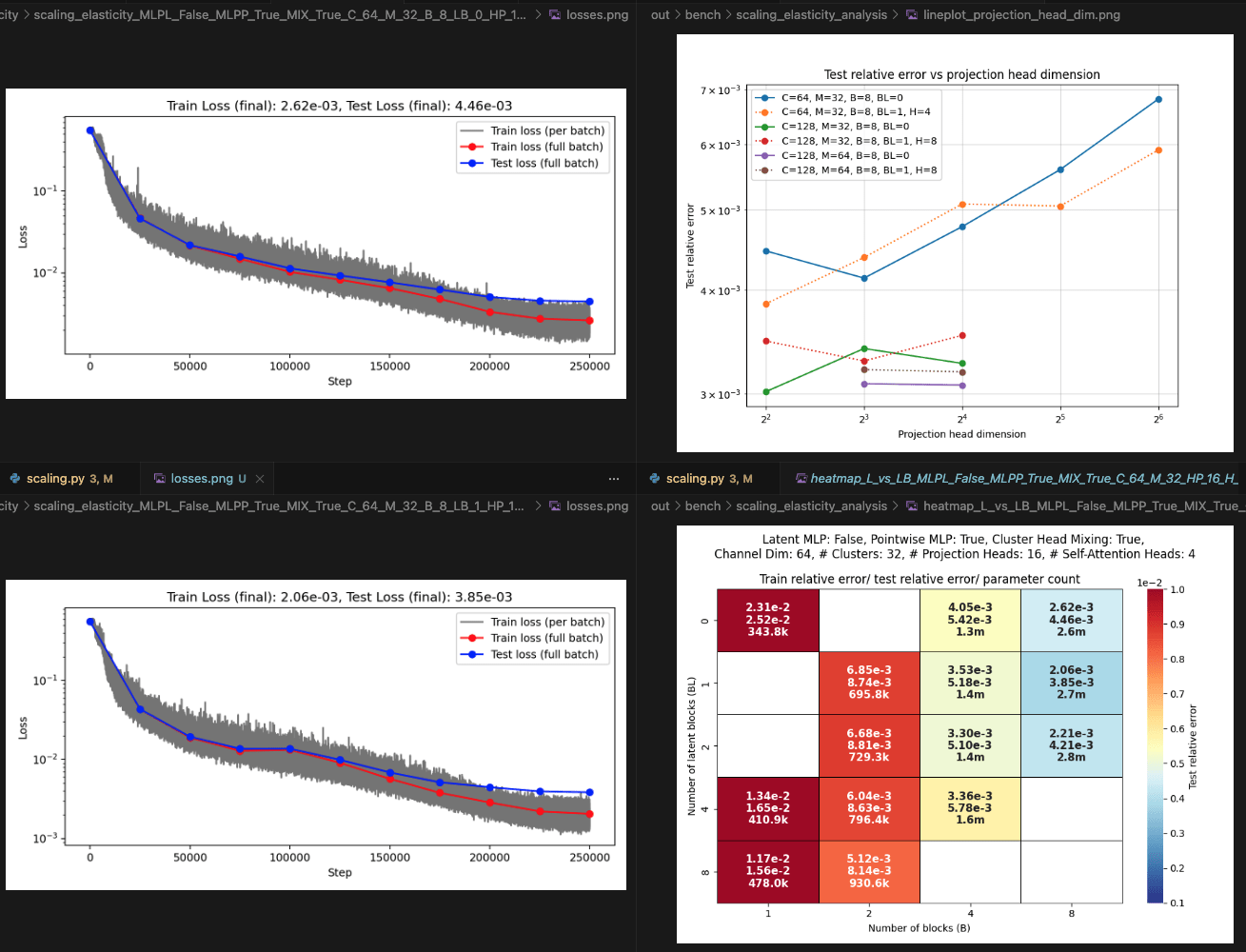
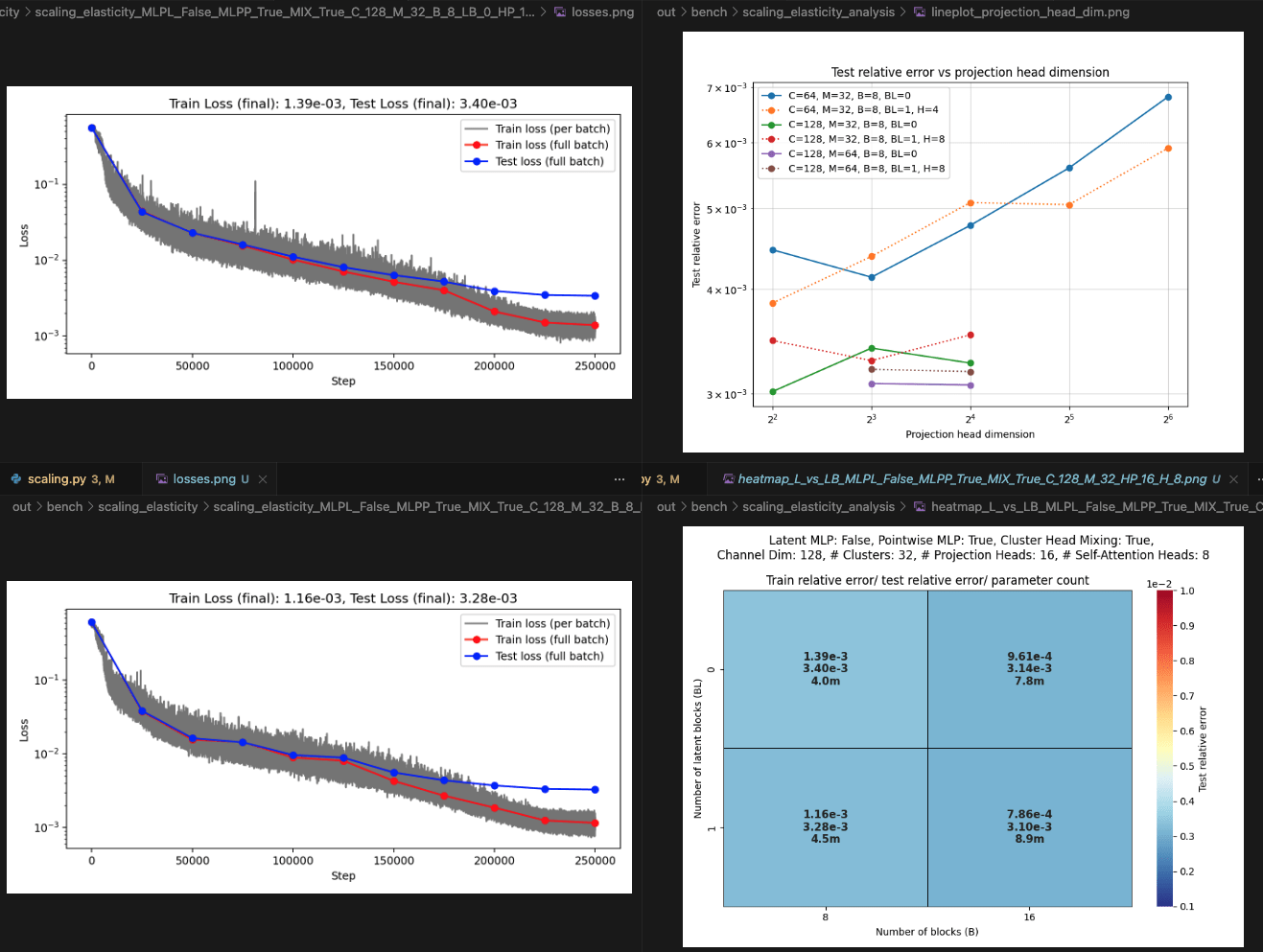
Elasticity: blocks vs layers scaling
Layers: Number of projections (latent encoding / decoding operations)
Blocks: Number of attention blocks in latent space in each layer.
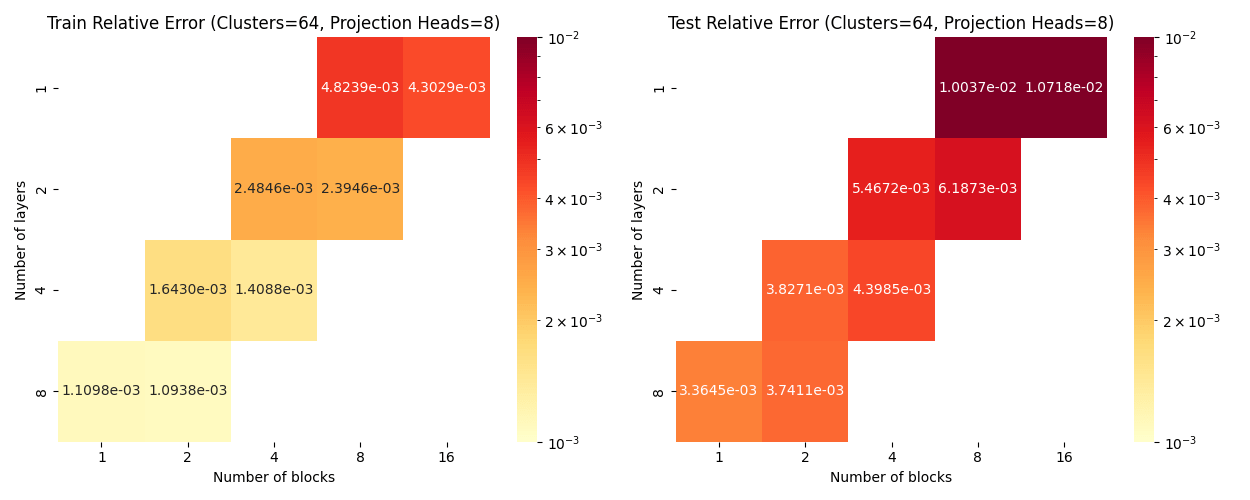
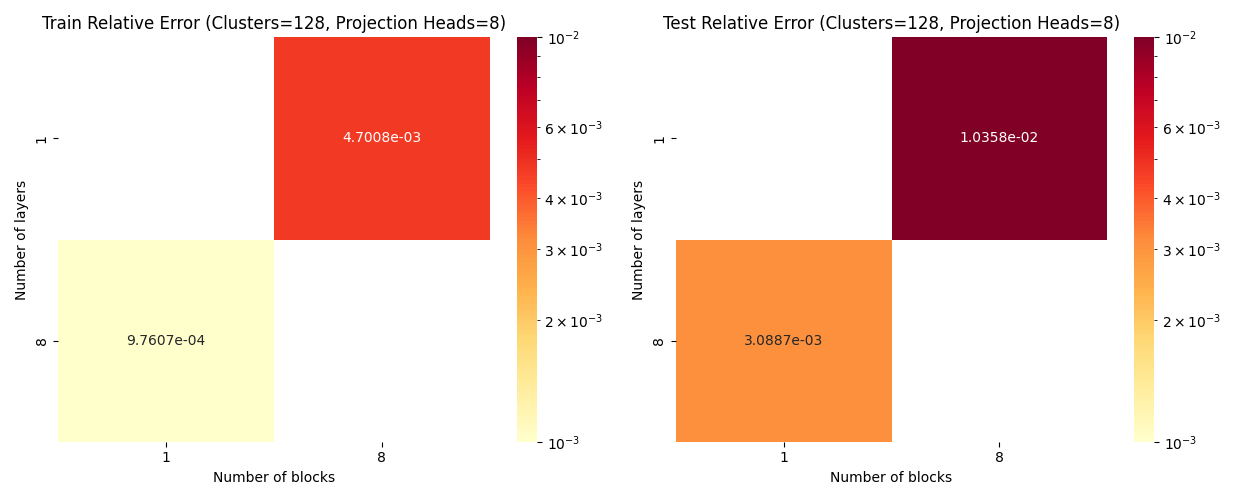
Layers: Number of projections (latent encoding / decoding operations).
Blocks: Number of attention blocks in latent space in each layer.
Projection heads: Number of latent encoding/ decoding projections happening in parallel in each layer.
Clusters: Projection dimension
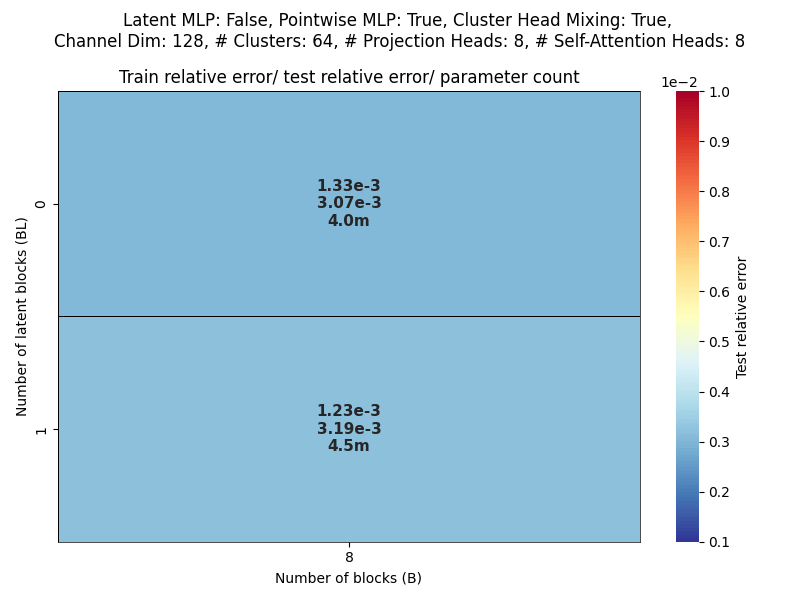
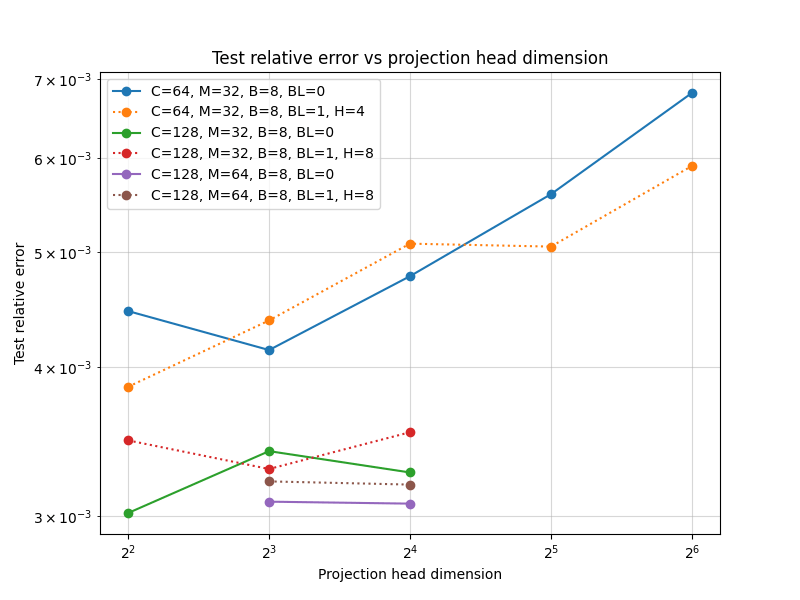
Elasticity: Scaling WRT Projection Heads
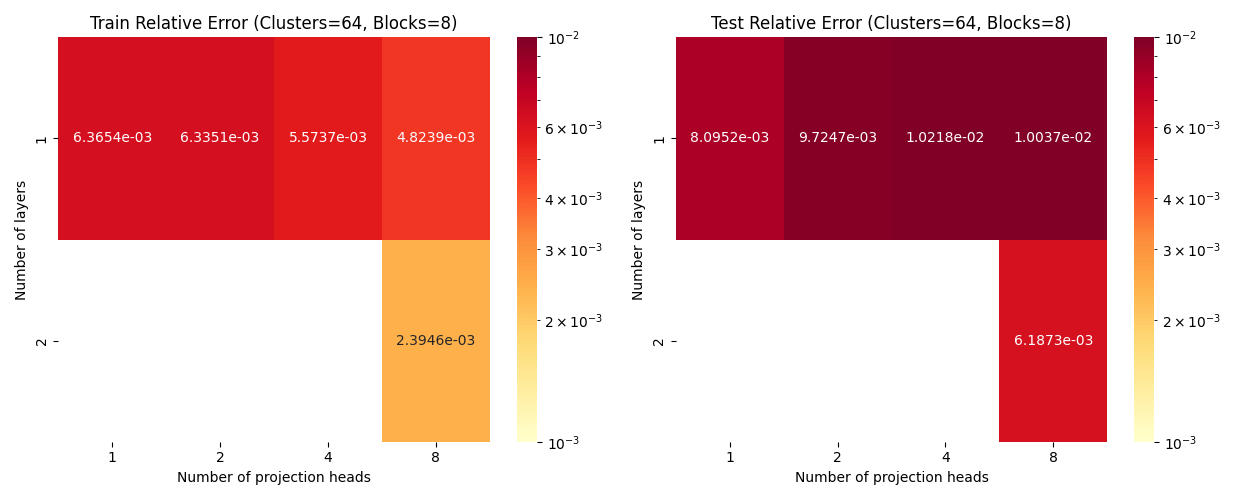
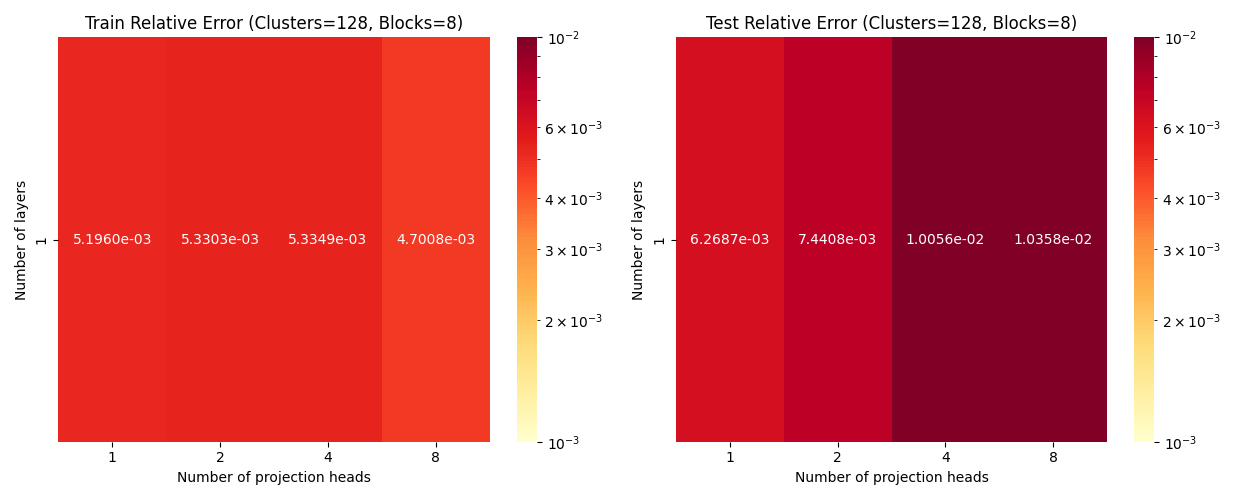
Layers: Number of projections (latent encoding / decoding operations).
Blocks: Number of attention blocks in latent space in each layer.
Projection heads: Number of latent encoding/ decoding projections happening in parallel in each layer.
Clusters: Projection dimension
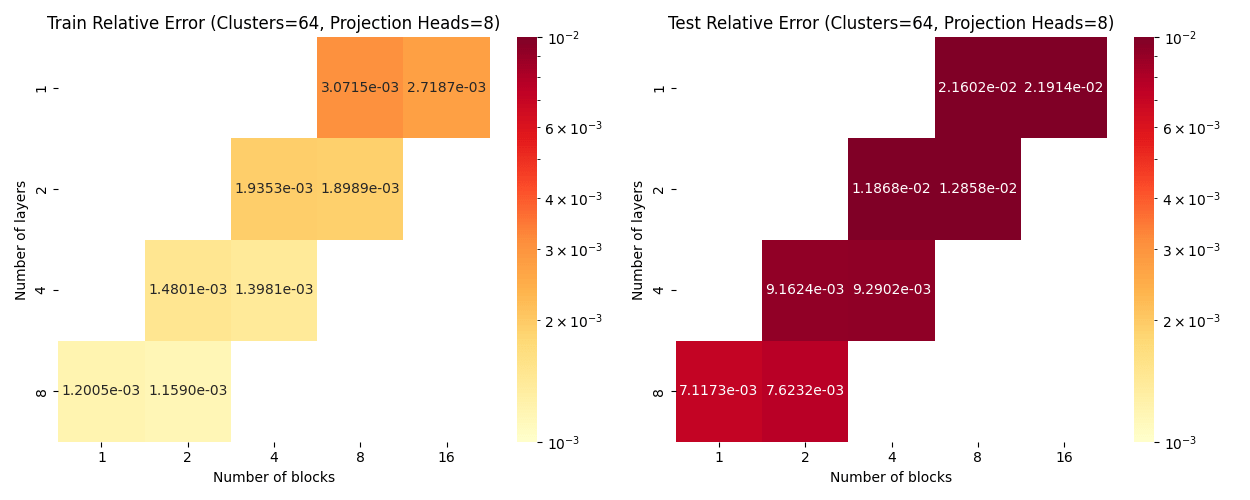
Darcy: blocks vs layers scaling
Layers: Number of projections (latent encoding / decoding operations)
Blocks: Number of attention blocks in latent space in each layer.
Layers: Number of projections (latent encoding / decoding operations).
Blocks: Number of attention blocks in latent space in each layer.
Projection heads: Number of latent encoding/ decoding projections happening in parallel in each layer.
Clusters: Projection dimension
Darcy: blocks vs layers scaling for different batch sizes
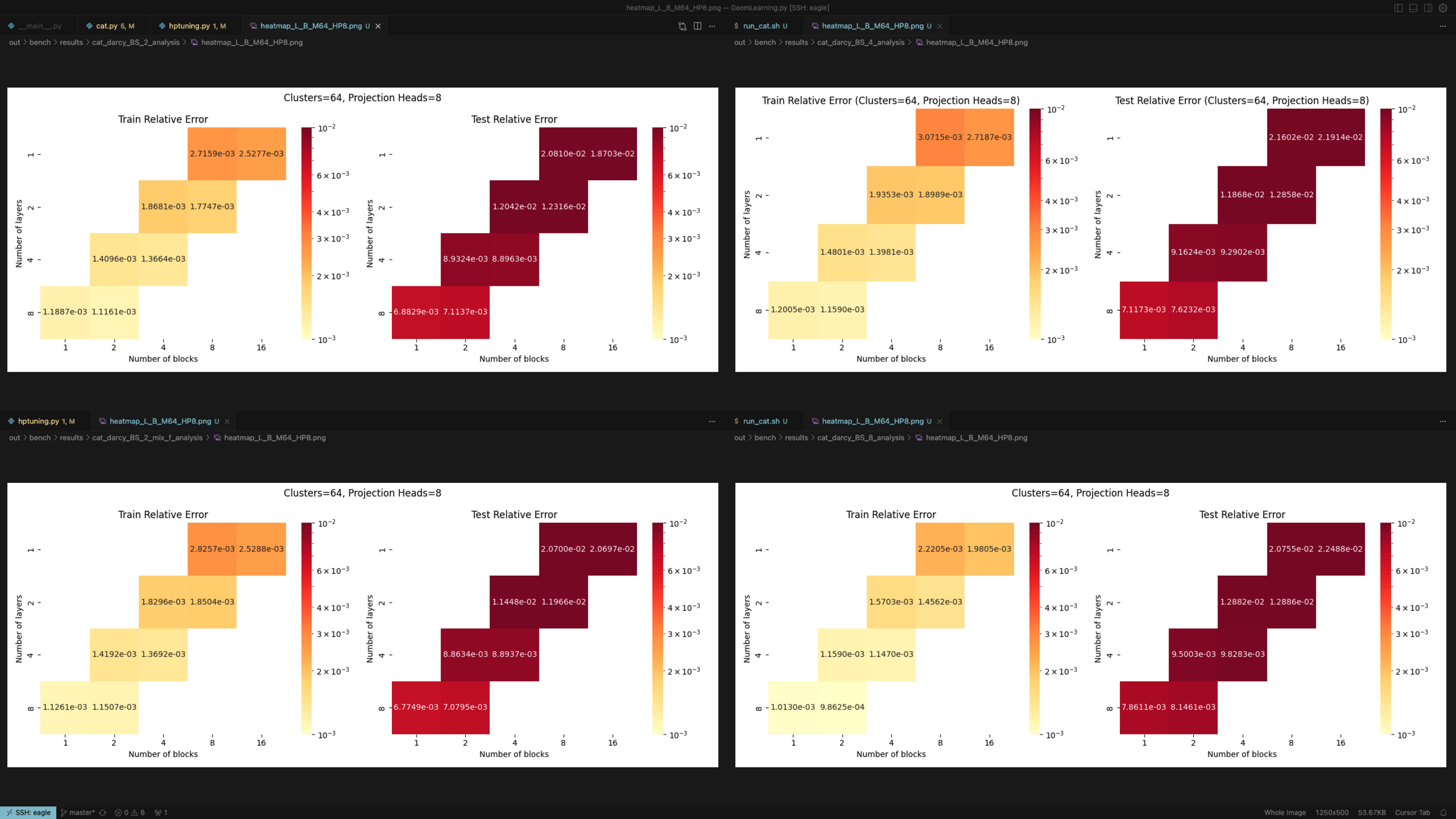
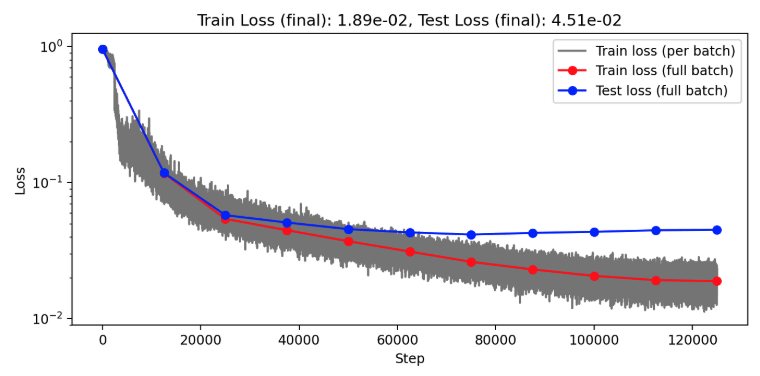
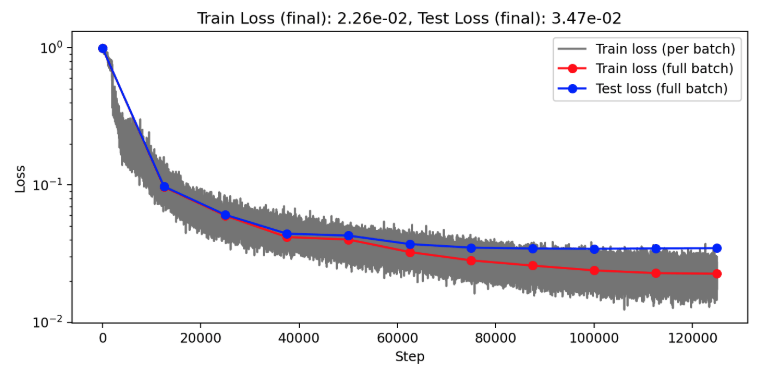
Darcy overfitting: Channels=64, Clusters=64, Layers=1, Blocks=8
MLP block in latent and pointwise space
MLP block in latent space only
MLP block in pointwise space only
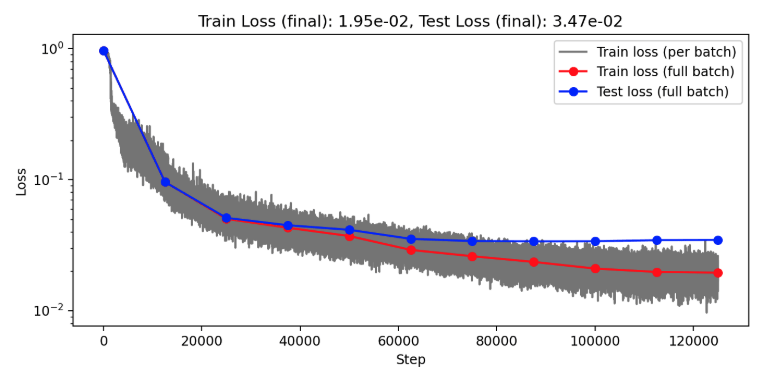
Projection Heads=4
Projection Heads=1
(Train/test) rel error: 5.765e-3 / 2.027e-2
(Train/test) rel error: 5.999e-3 / 1.440e-2
(Train/test) rel error: 7.363e-3 / 1.465e-2
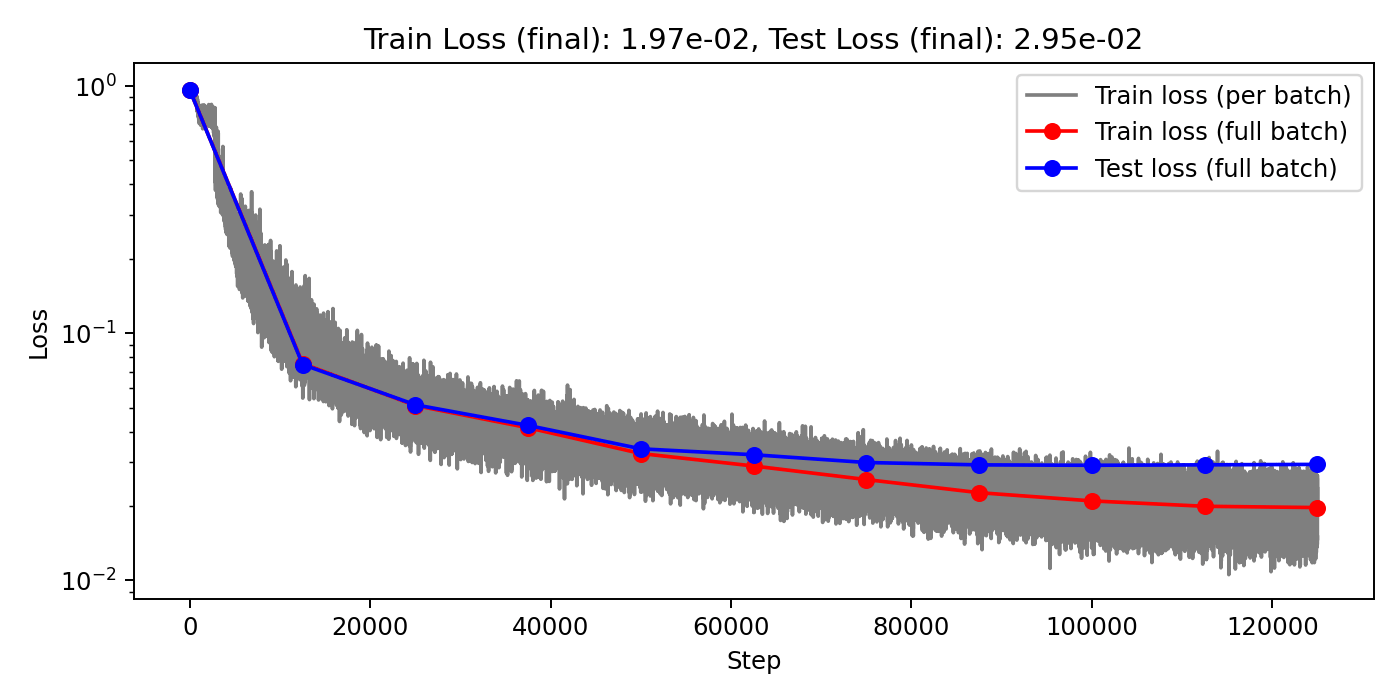
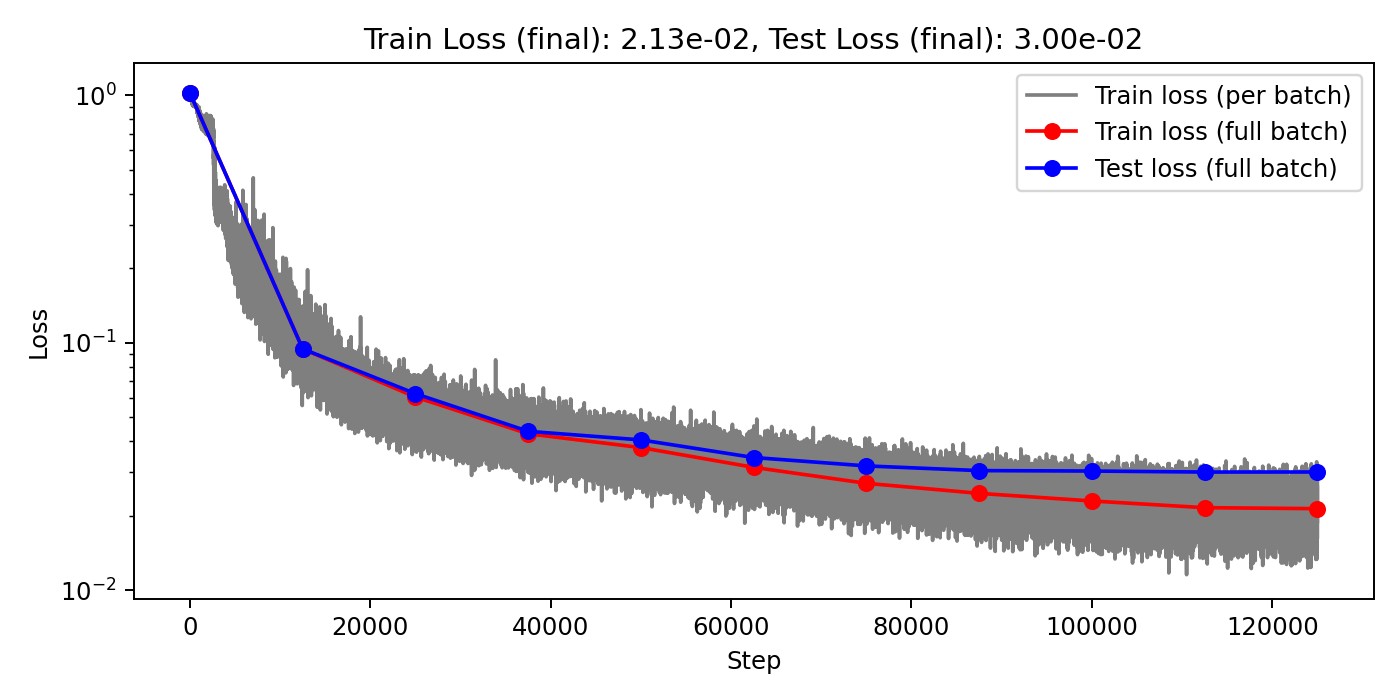
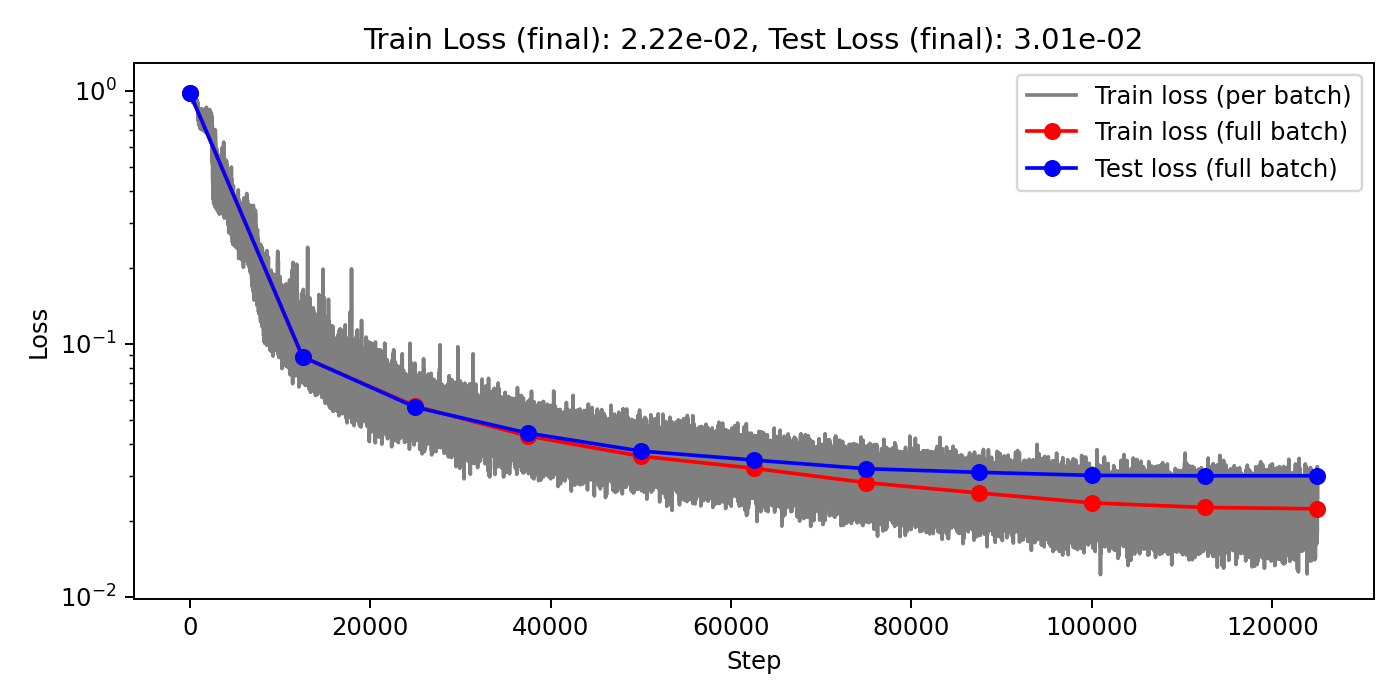
(Train/test) rel error: 6.076e-3 / 1.144e-2
(Train/test) rel error: 6.776e-3 / 1.182e-2
(Train/test) rel error: 7.234-3 / 1.176e-2
Darcy overfitting: Channels=64, Clusters=64, Layers=8, Blocks=1
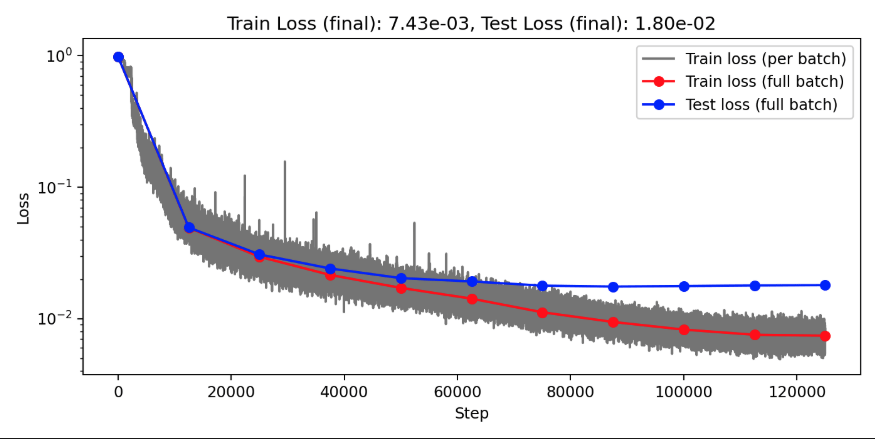
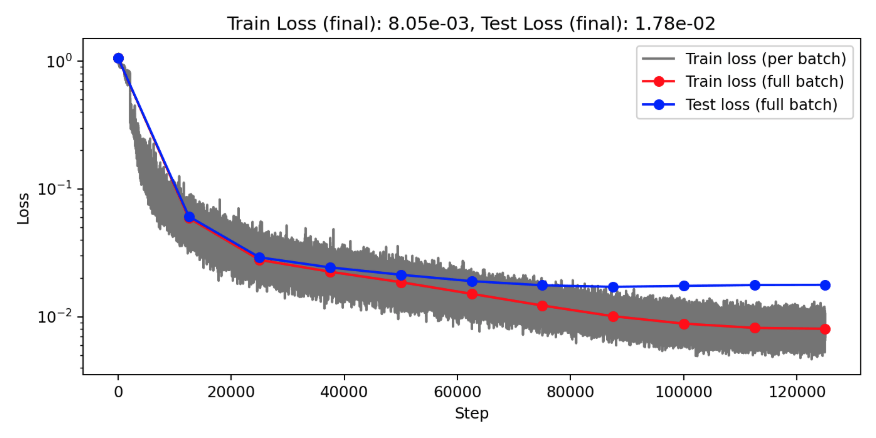
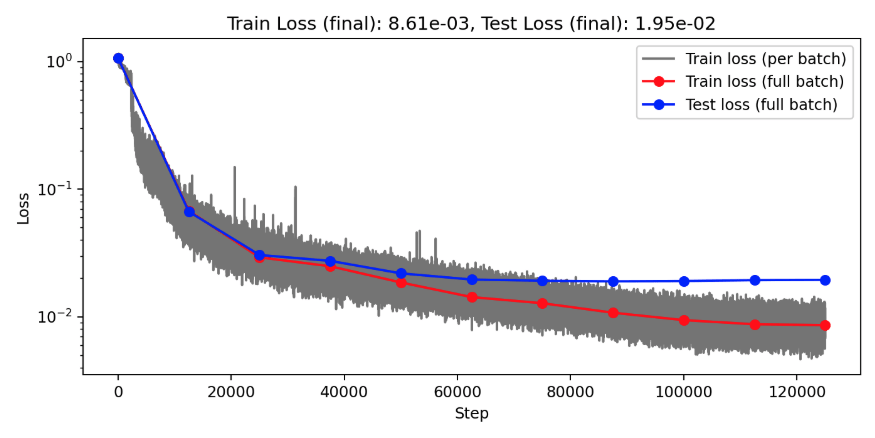
Projection Heads=4
(Train/test) rel error: 1.915e-3 / 6.935e-3
(Train/test) rel error: 2.243e-3 / 7.581e-3
(Train/test) rel error: 2.078e-3 / 7.101e-3
Projection Heads=1
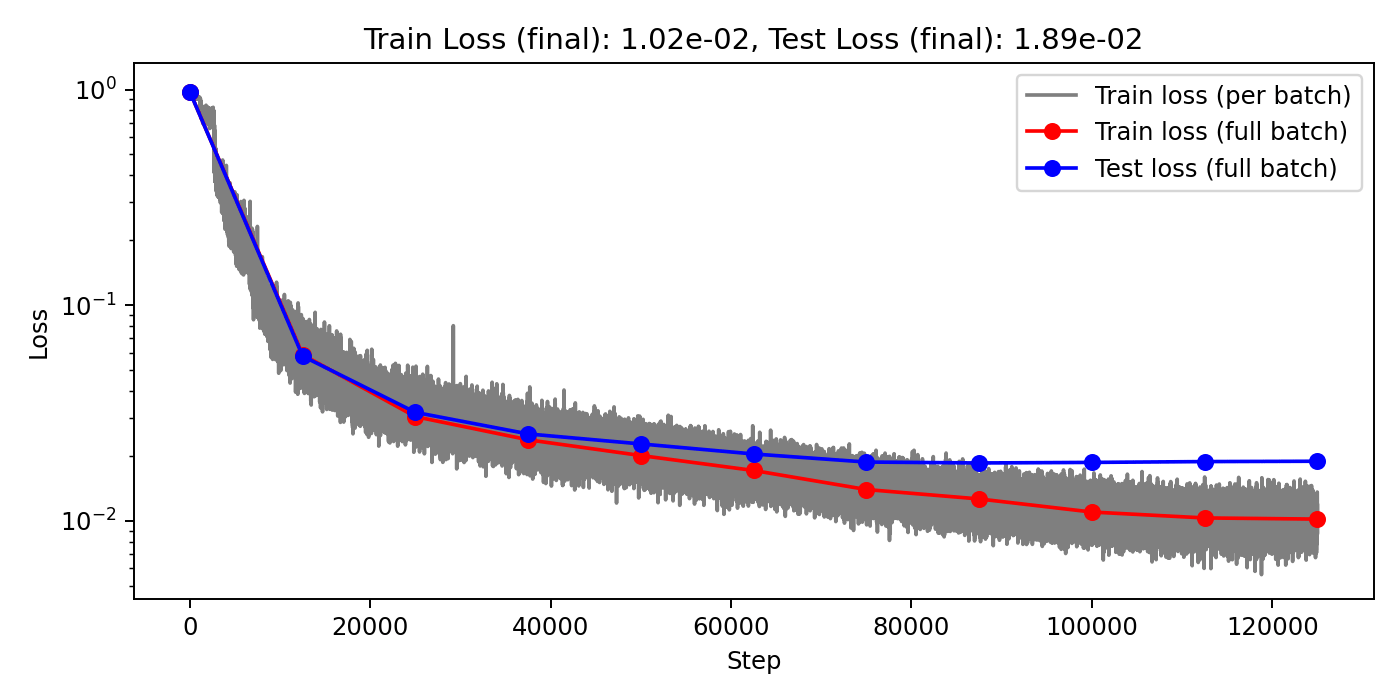
(Train/test) rel error: 2.780e-3 / 6.956e-3
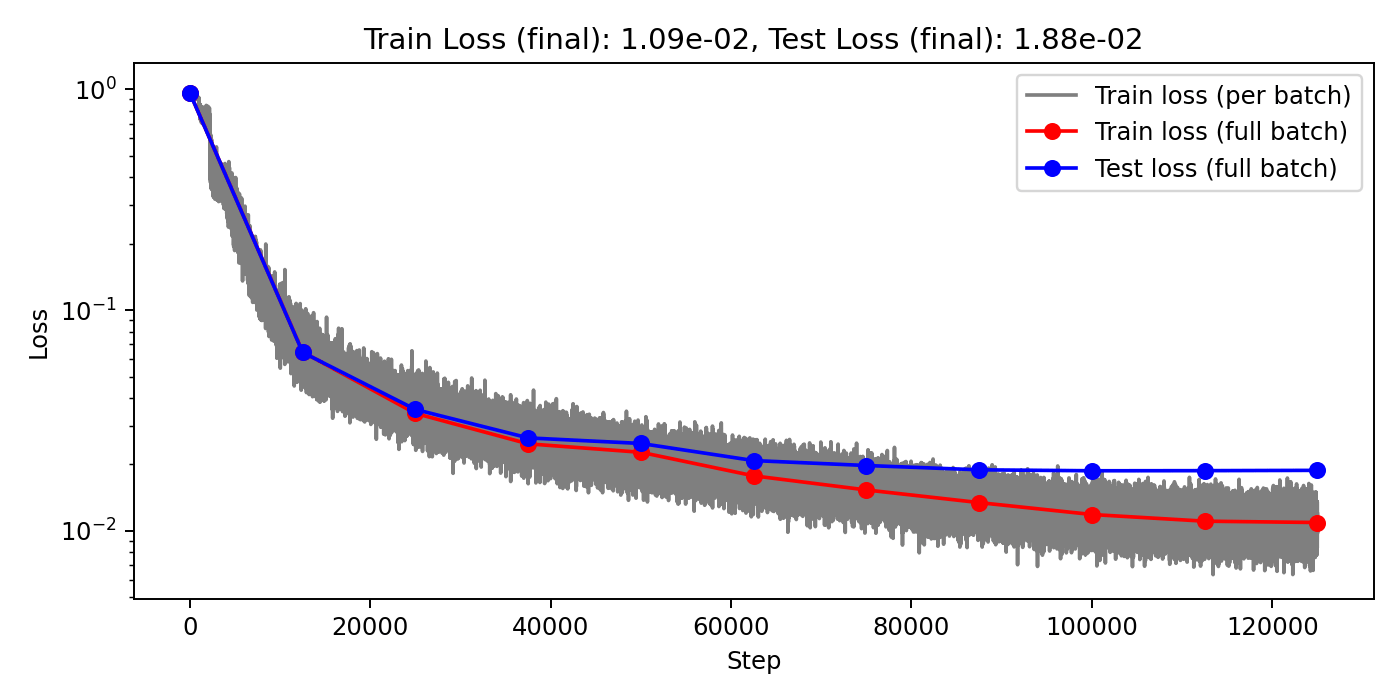
(Train/test) rel error: 2.999e-3 / 6.918e-3
MLP block in latent and pointwise space
MLP block in latent space only
MLP block in pointwise space only
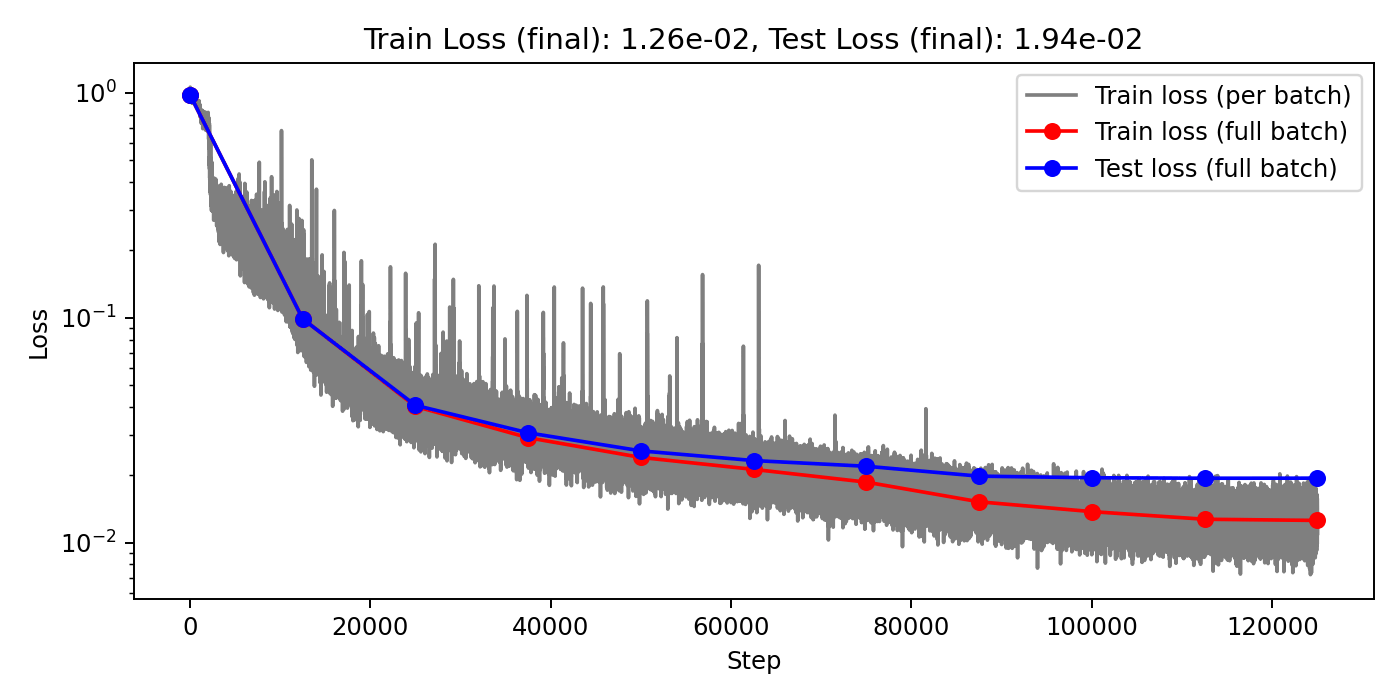
(Train/test) rel error: 3.526e-3 / 7.109e-3
Cluster Attention Transformer

CAT Block
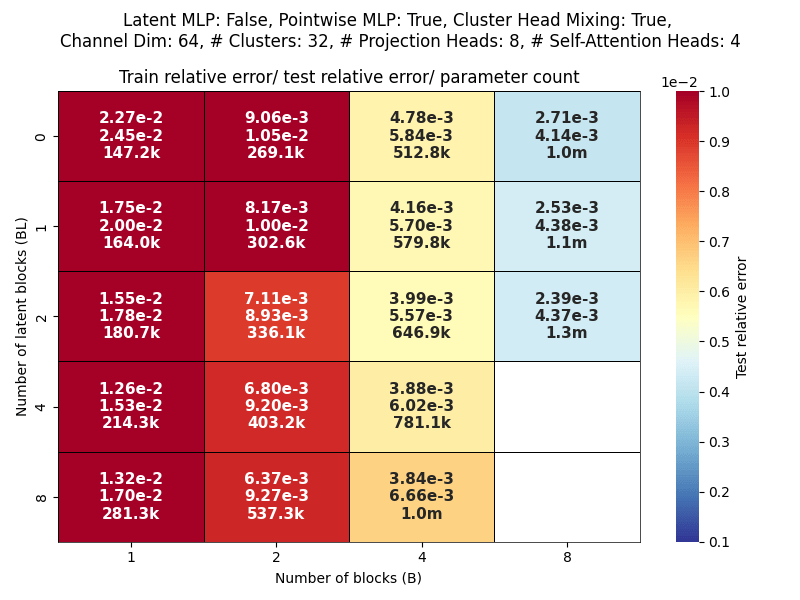
Scaling study
Channel dim: Model working dimension.
Blocks: Number of CAT projection blocks (latent encoding / decoding operations).
Latent Blocks: Number of self-attention blocks in latent space in each CAT block.
Projection heads: Number of latent encoding/ decoding projections happening in parallel in each layer.
Clusters: Projection dimension
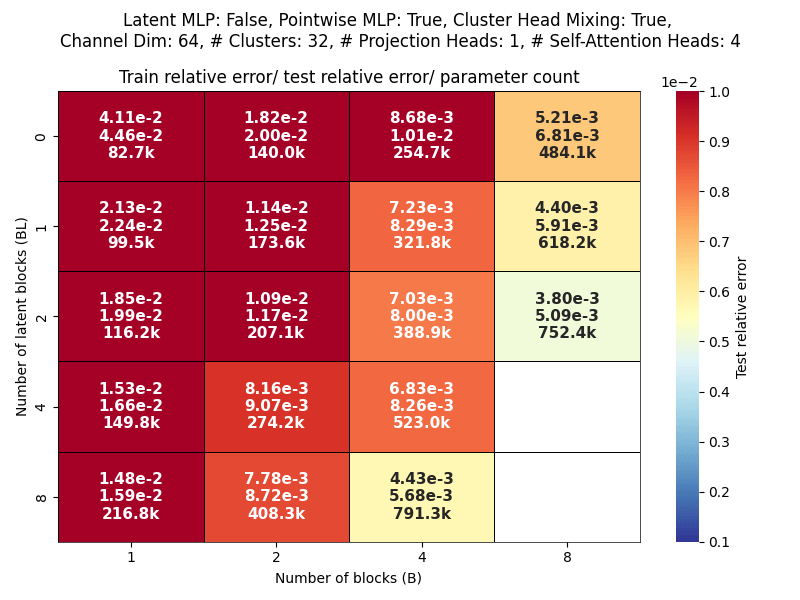
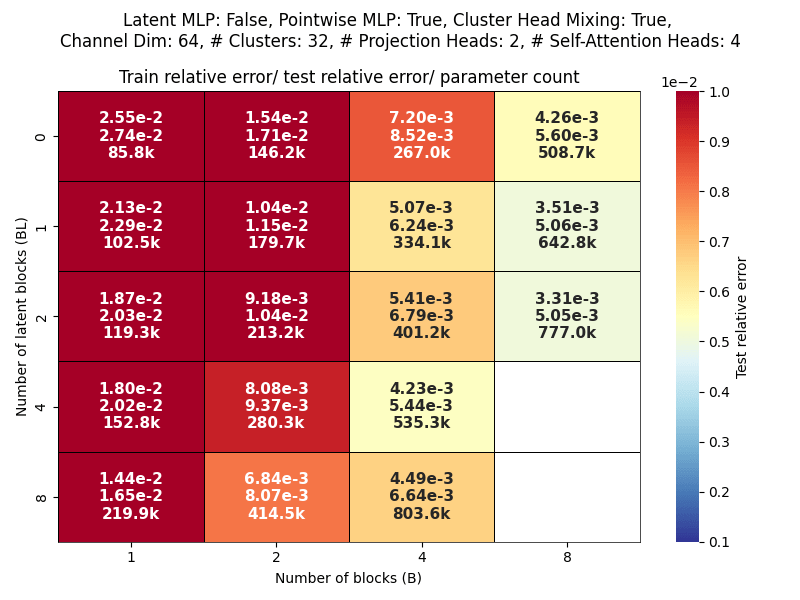
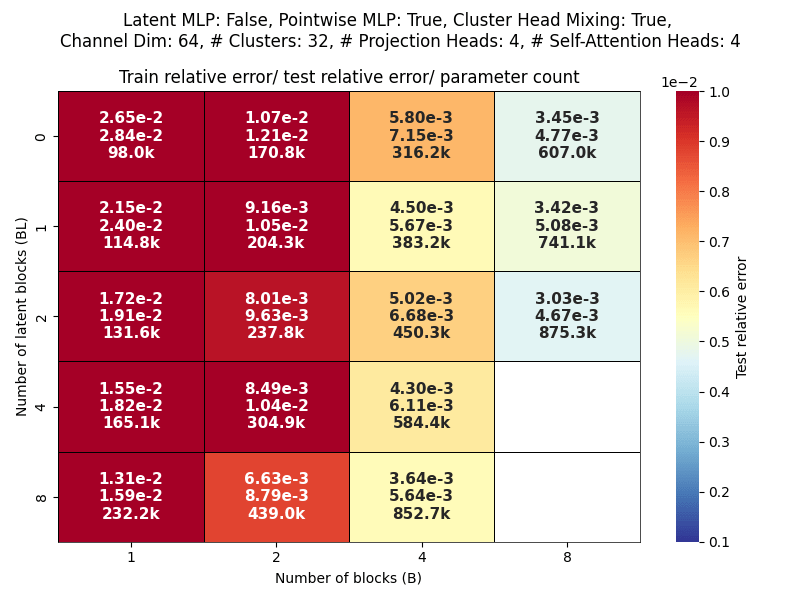
Scaling study
OBSERVATIONS:
- More CAT blocks, fewer latent blocks!
- Expected
- Greater projection heads work better!
- Validates our approach of
multiple parallel projections
- Validates our approach of
- With many projection heads,
CAT works well with no latent blocks!- SURPRISING!




Scaling study
OBSERVATIONS:
- More CAT blocks, fewer latent blocks!
- Expected
- Greater projection heads work better!
- Validates our approach of
multiple parallel projections
- Validates our approach of
- With many projection heads,
CAT works well with no latent blocks!- SURPRISING!
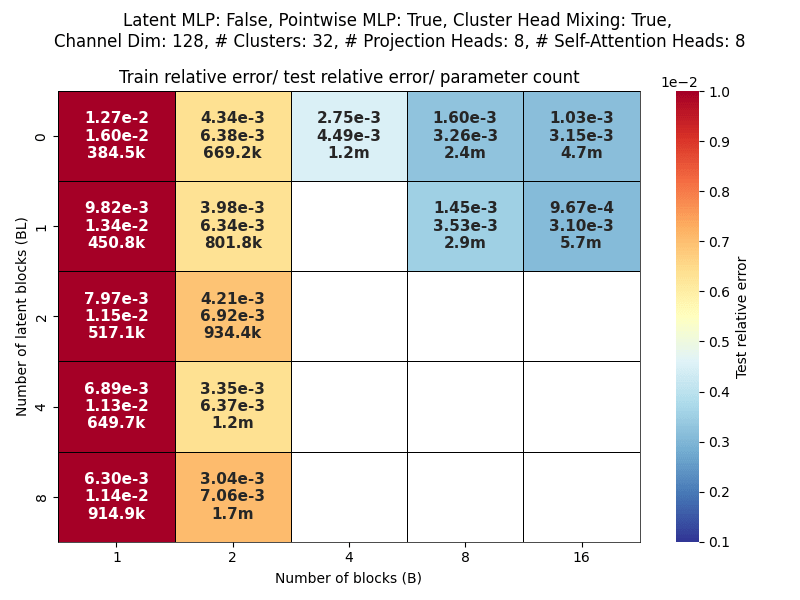
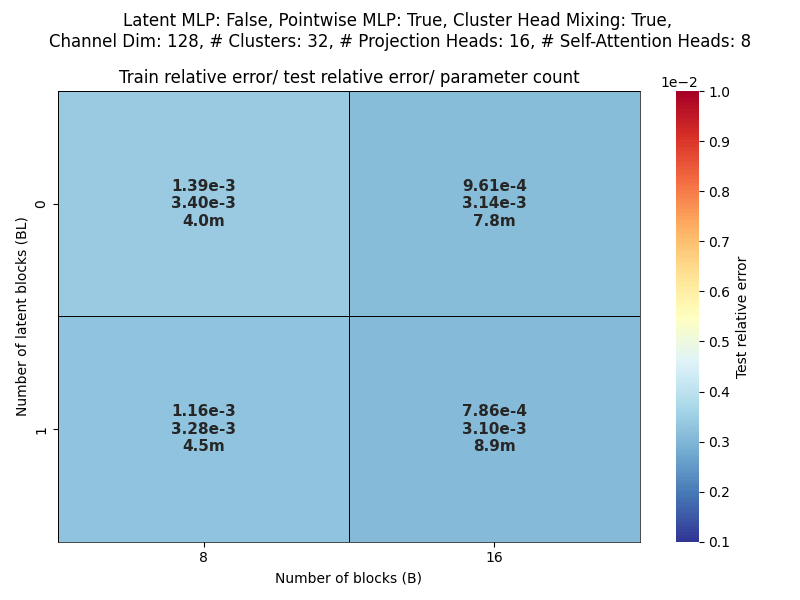
Scaling study
- During projection, each cluster is amassing information from hundreds/thousands of points.
- This is like a pooling (averaging) operation
- Then cluster values are projected (copy-pasted) back to point cloud.
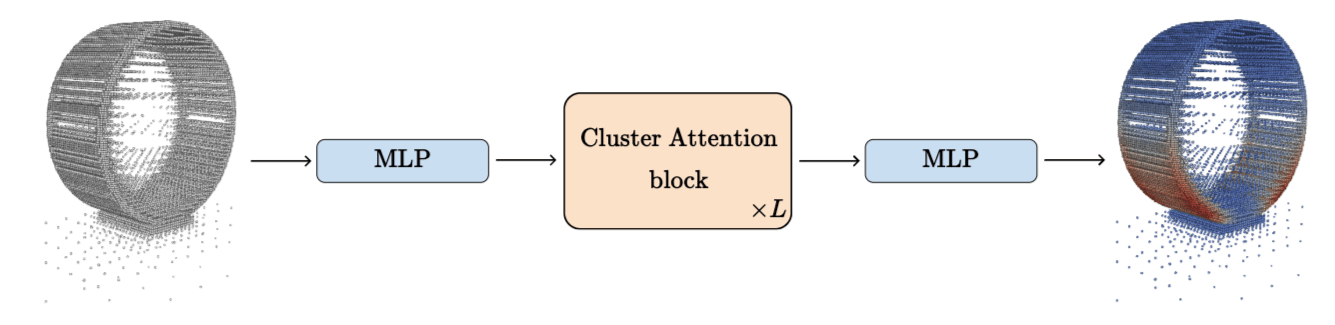
CAT with Latent Blocks = 0
- Project to many sets of cluster locations with
- All-to-all interaction among projection weights (before projection).
- Project back to point cloud
Transolver
- Project to 1 set of slices
- Attention among slices
- Project back to point cloud

Scaling study
OBSERVATIONS:
- More CAT blocks, fewer latent blocks!
- Expected
- Greater projection heads work better!
- Validates our approach of
multiple parallel projections
- Validates our approach of
- With many projection heads,
CAT works well with no latent blocks!- SURPRISING!
\( = \frac{\text{Channel dim}}{\text{Number of projection heads}}\)
Scaling study
Scaling study
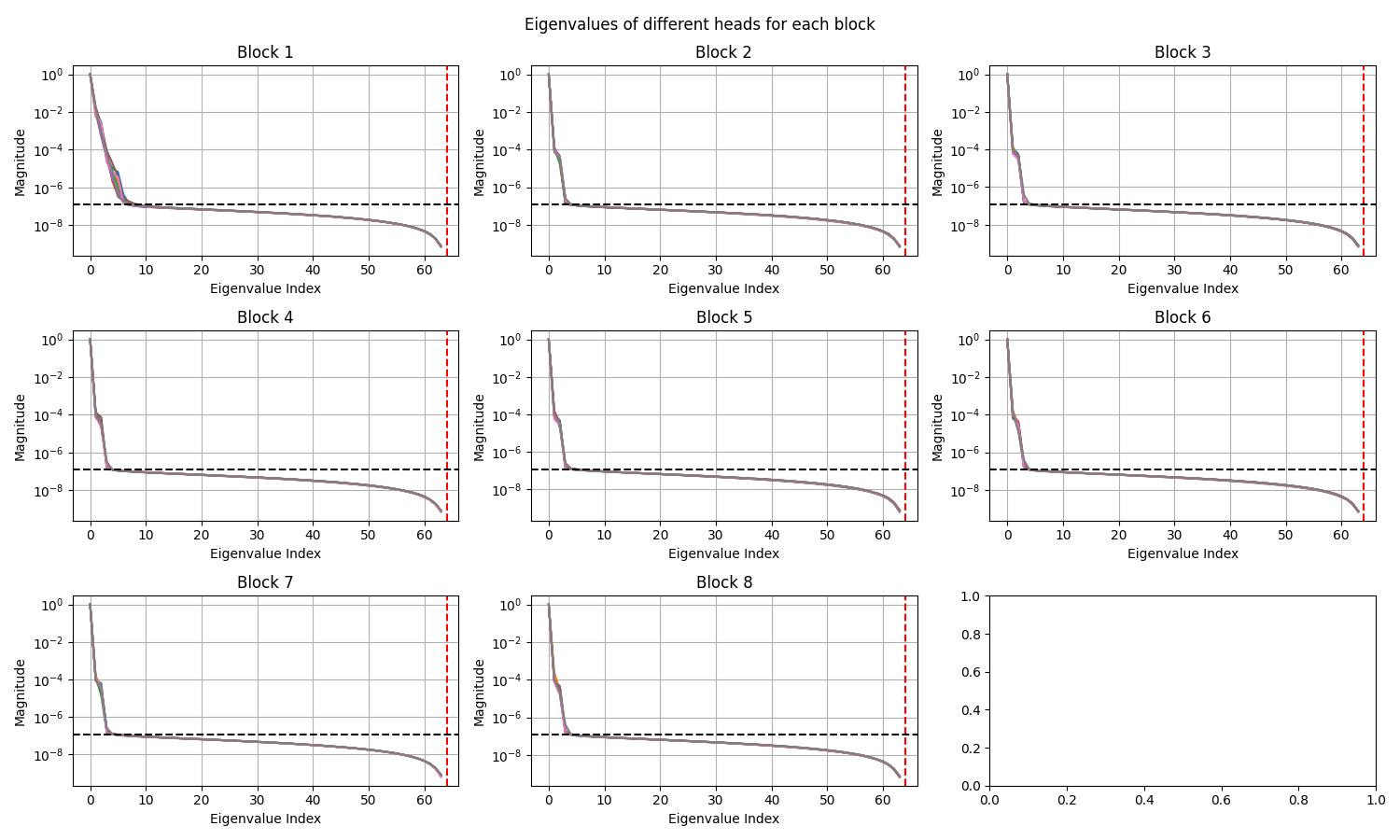
Elasticity: Decay in singular values in different layers (EPOCH 0)
Elasticity: Decay in singular values in different layers (EPOCH 500)
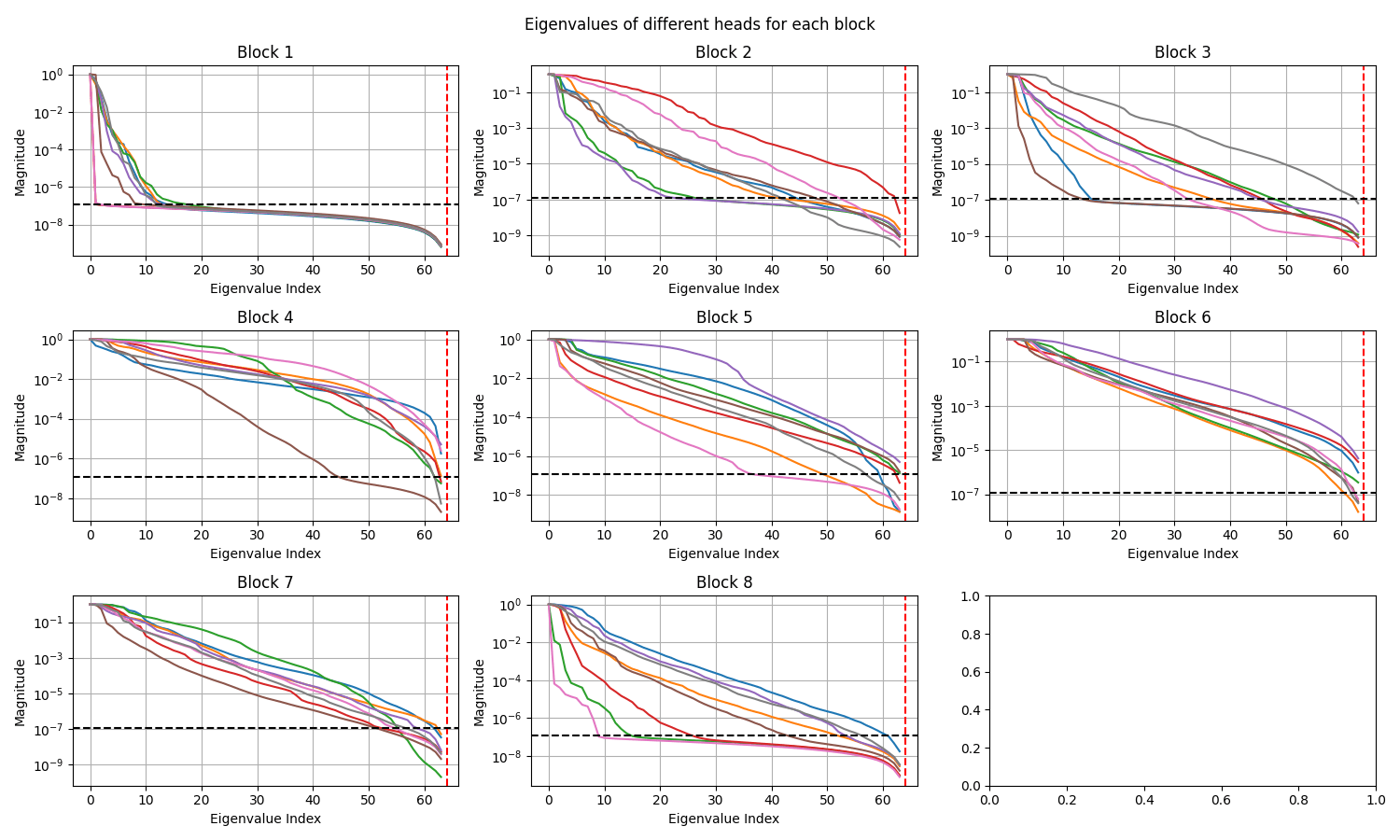
Elasticity: Decay in singular values in different layers (EPOCH 500)

ShapeNet-Car: Decay in singular values in different layers
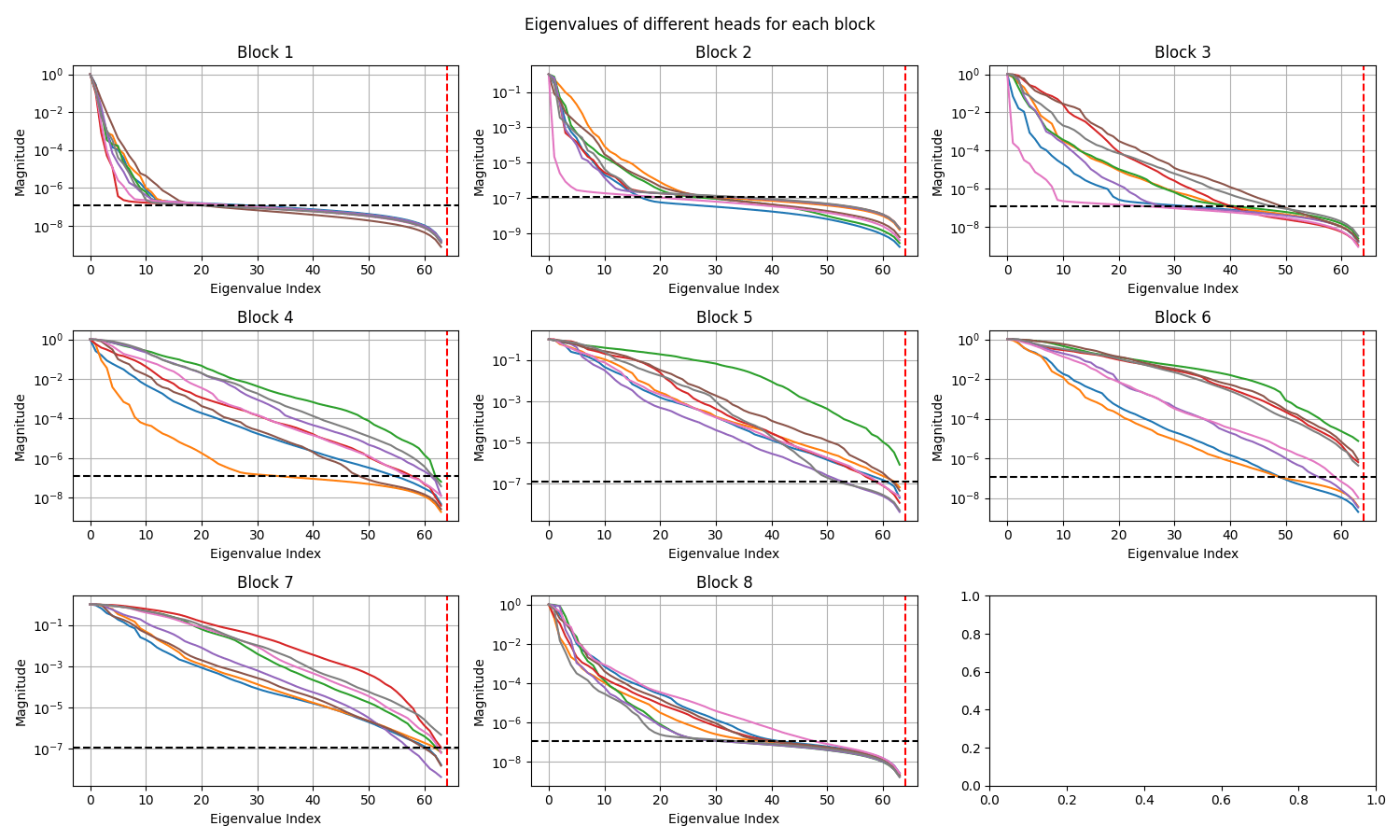
Darcy: Decay in singular values in different layers
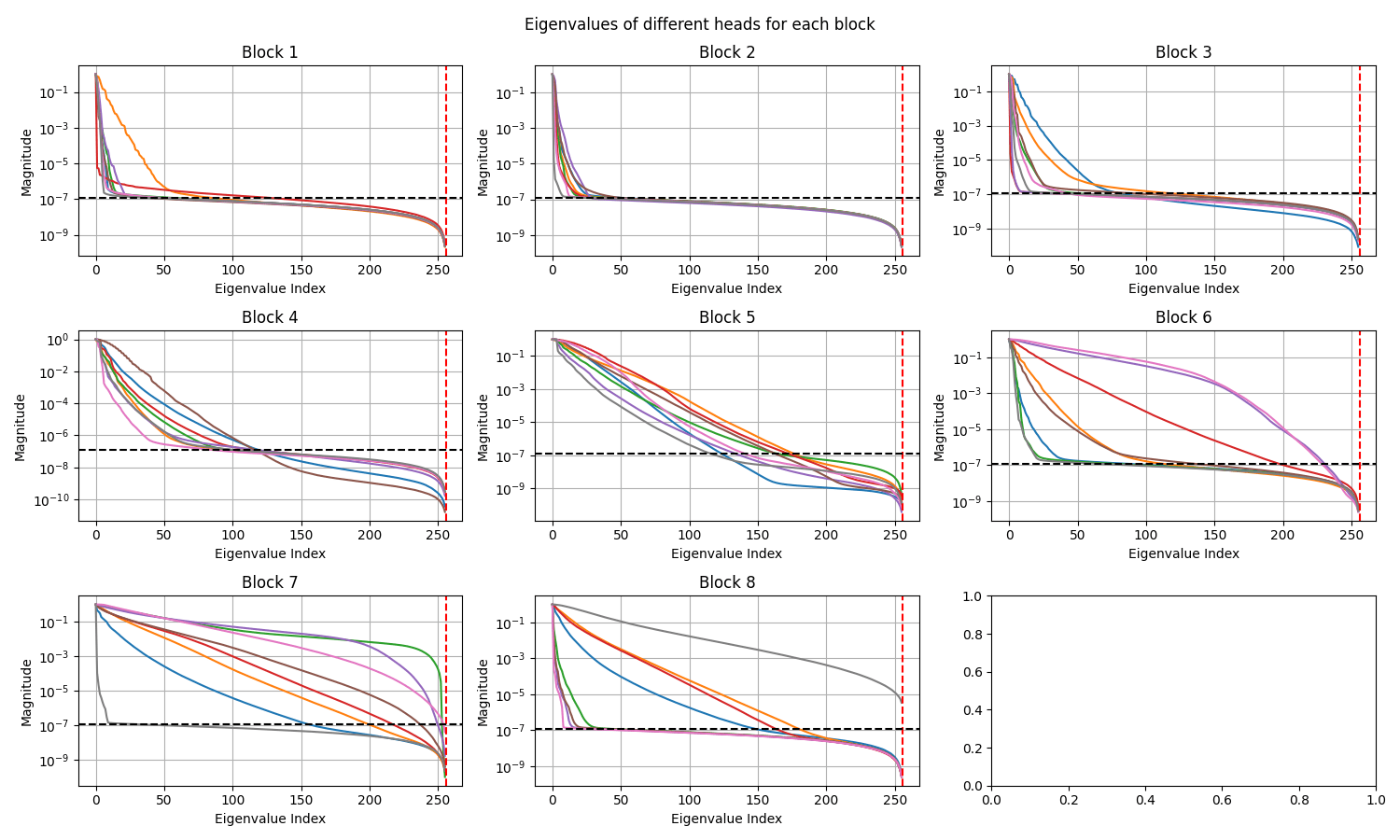

Latent Cross-Attention (DCA)
Expressive transformer architecture
TASKS
- [~] Figures
- [~] Method exposition
- [~] Mathematical analysis, discussion
- [X] CUDA kernel implementation
- [ ] Scaling, ablations
APPLICATIONS
- [X] PDEs
- [~] Point cloud segmentation/ classification
- [X] ModelNet40 Classification
- [~] ScanNet semantic segmentation
- [ ] S3DIS semantic segmentation
-
[~] Image classification, diffusion- Requires comprehensive hyperparameter tuning
- Better to focus on this in future work
FUTURE WORK
- DCA for CV tasks
- Foundation model for 3D shape understanding
- Ref. ShapeLLM
FLARE scaling study
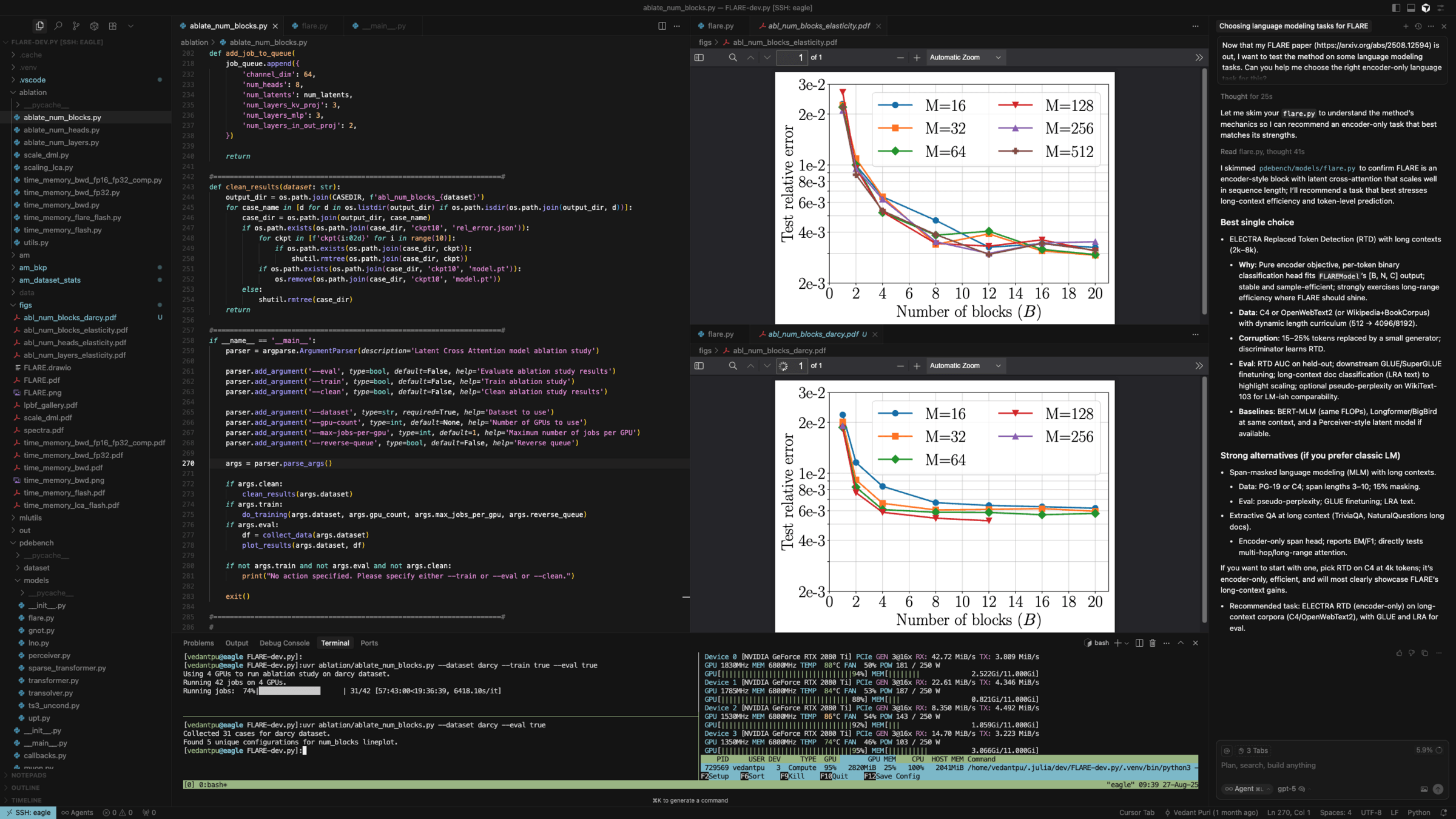
Weekly meeting - 10/23/25
PROPOSAL
- Waiting on Prof. Farimani for scheduling. Potential dates:
NEXT PAPER - ICML (Int'l conference of Machine Learning)
- Triple attention method
- Competitive with FLARE on PDE problems
- Multilinear attention method (maybe)
WINTER BREAK PLAN - visit India Dec 11 - Jan 10
- Attend wedding Dec 12 - 14
- Work remotely the weeks of Dec 15
- Take off the week of Dec 22
- Work remotely week of Jan 5

PROGRESS
- Setting up Long Range Arena benchmark problems for FLARE reviews.
- Wrote CUDA kernels to make triple attention method as efficient as FLARE
- Fixed numerical instabilities with FP16 training
- Fixed issue with Darcy dataset (removed downsampling)
- Testing triple attention with different kernels (parameter study)
NEXT STEPS
- Decide on PDE experimental suite for Triple attention
- Test on Long Range Arena benchmarks
- Set up toy problems that demonstrate advantage of three-way attention.
Weekly meeting - 10/30/25
PROPOSAL
- Dec 4, 2025 - Scaife 309 B
NEXT PAPER - ICML (Int'l conference of Machine Learning)
- Triple attention method
- Competitive with FLARE on PDE problems
- Multilinear attention method (maybe)
PROGRESS
- Finish additional benchmarks for FLARE paper (w. MS student Datta)
- Testing triple attention with different kernels
- Setting up representative toy problems
- Testing models on reasoning based on recent paper
- Started work on proposal report and slides
NEXT STEPS
- Test Triple on LRA
- Set up toy problems that demonstrate advantage of three-way attention.
Triple attention vs FLARE scaling
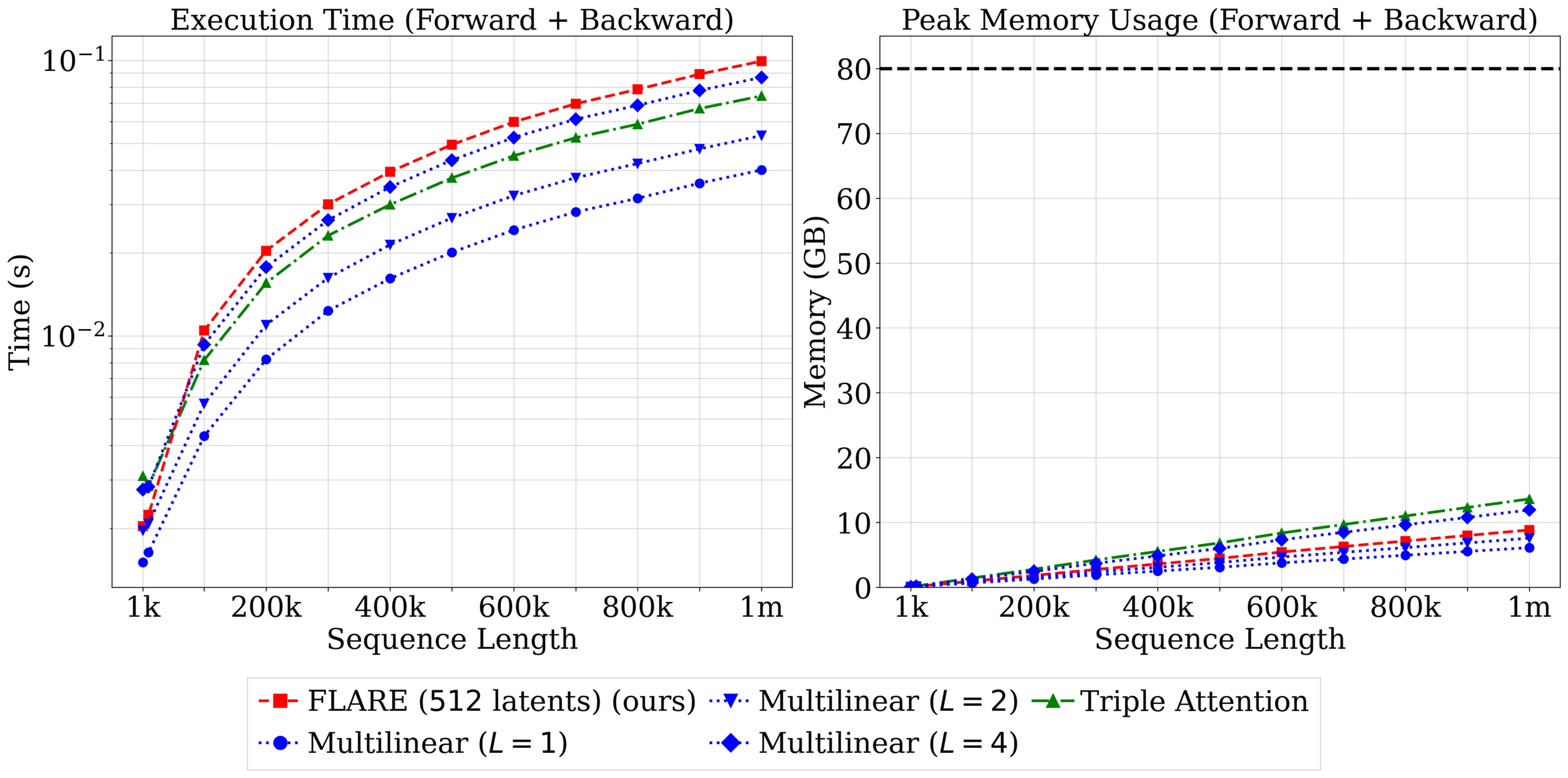
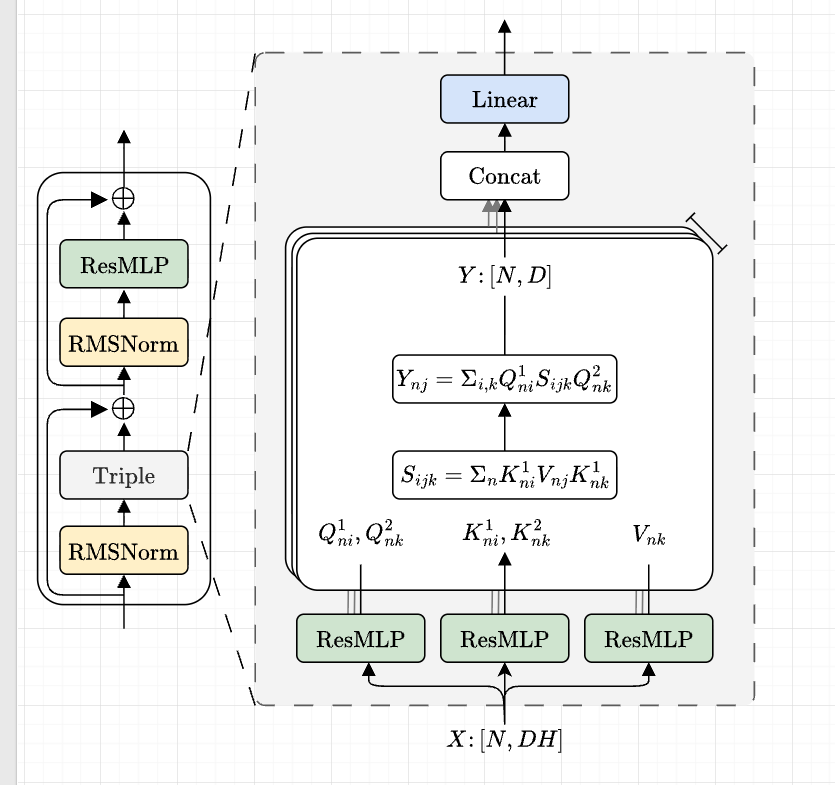
Triple attention vs FLARE on Darcy (58k): C=128, B=8
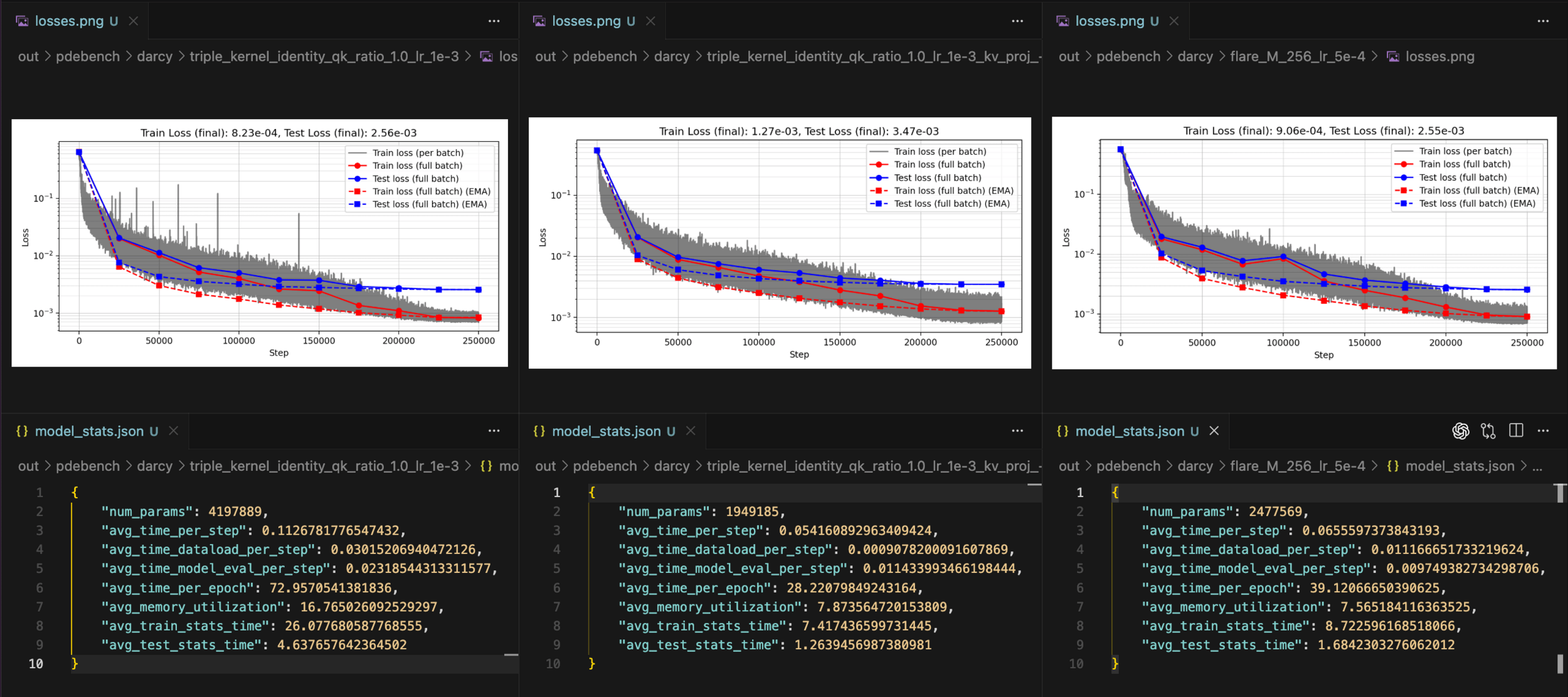
Triple v1 (4.2m)
Triple v2 (1.9m)
FLARE (2.4m)
Different depths of ResidualMLPs
ROM Project
Nonlinear kernel parameterizations for Neural Galerkin
- Equation-based, data-free numerical methods for solving PDEs
- Fast PDE solve in comparison to FEM thanks to compact representation
- Smaller representation, faster solve in comparison to ML-based ROMs
Status and plan
- Promising preliminary results on a host of 1D problems
- Need at least 1 semester of time to flesh out these ideas
Potential new contributions and timeline
- Develop and finalize proposed parameterizations (1-2 moths)
- Test different parameterization ideas
- Test on 1D, 2D test cases
- Develop adaptive refinement/ coarsening techniques (1 month)
Parameterized Tanh kernels
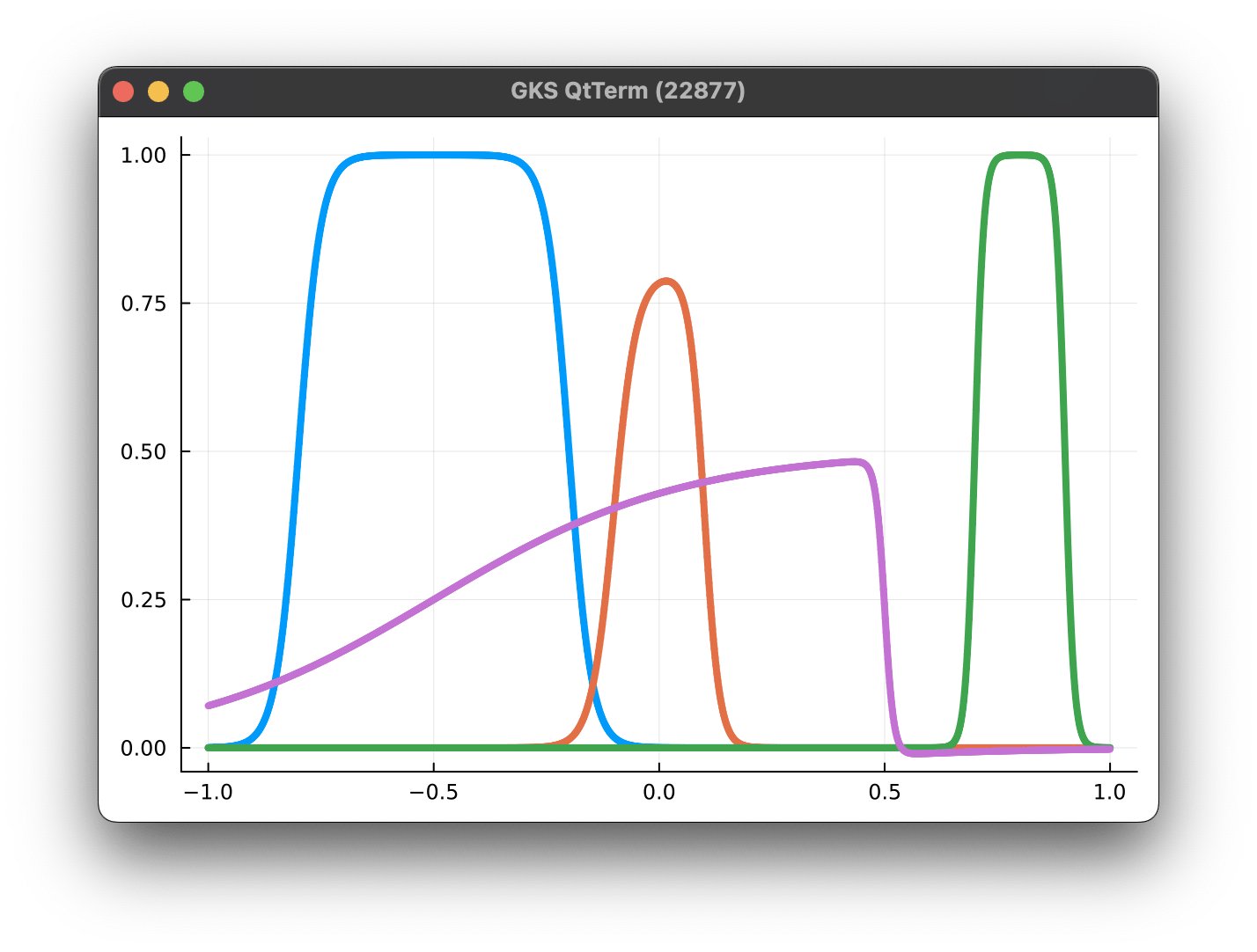
ROM Project - Nonlinear parameterizations
Nonlinear kernel parameterizations for Neural Galerkin
- Equation-based, data-free numerical methods for solving PDEs
Status and plan
- Promising preliminary results on a host of 1D problems
- Need at least 1 semester of time to flesh out these ideas
Potential new contributions and timeline
- Develop novel parameterizations that have several benefits
- Very expressive (handles shocks) with few parameters (speedup)
- Fast hyper-reduction as parameterization is naturally sparse
- Accurate integration as parameterization is sparse
- In comparison, DNNparameterizations are large and do not result in a speedup; other kernelized parameterizations (e.g. Gaussian kernels) are not as expressive
- Develop adaptive refinement techniques
- Develop adaptive coarsening techniques

Parameterized Tanh kernels

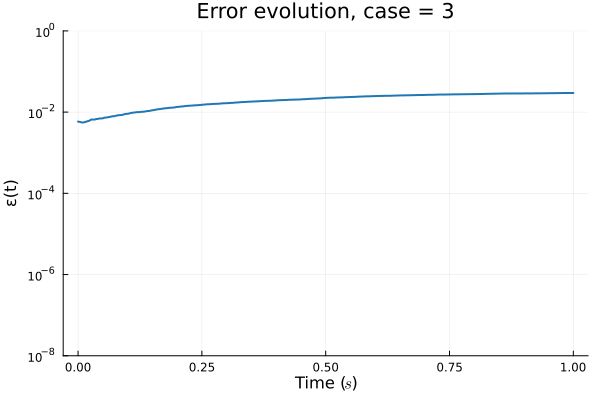
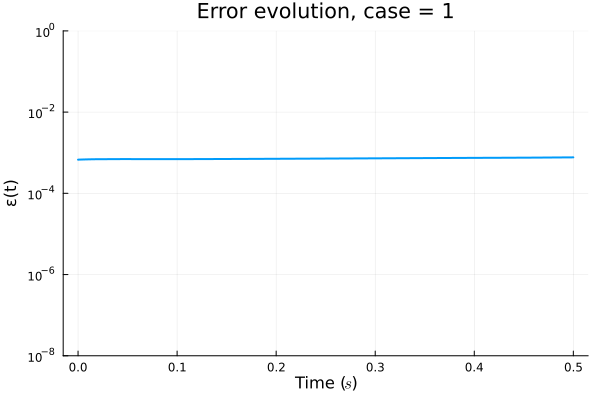
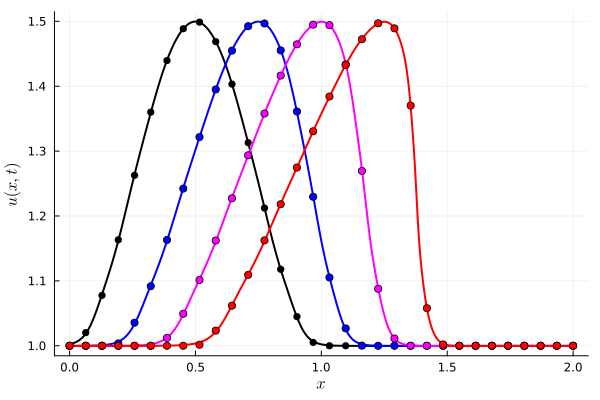
Neural Galerkin - Advection Diffusion problem
Parameterized Gaussian (OURS)
3 parameters
8 collocation points
Deep Neural Network (BASELINE)
~150 parameters
256 collocation points
Multiplicative filter network (MFN)
~210 parameters
256 collocation points
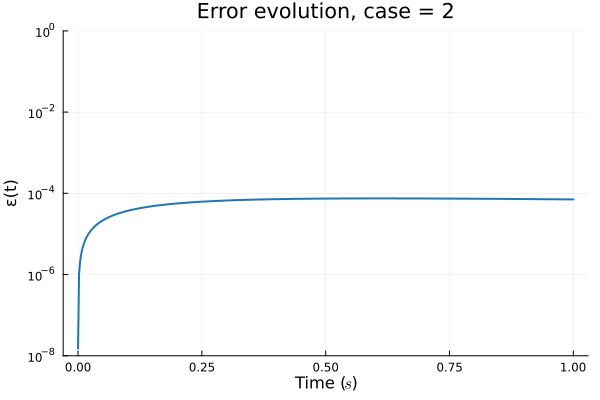
Error due to limited expressivity of this simple model
FAILED TO CONVERGE
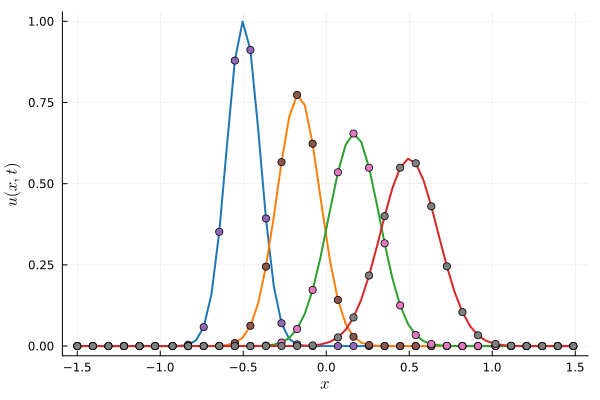
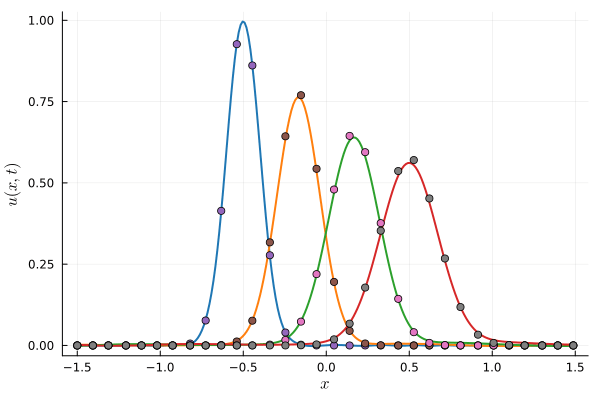
Improve model fit by splitting kernels
- At time t=0, we are fitting the initial condition given to us with our nonlinear model. This is the projection step.
- To improve the fit, we are going to make the model more expressive with boosting.
- We do this by repeatedly dividing each kernel in two and optimizing both.
- This is akin to adaptive refinement
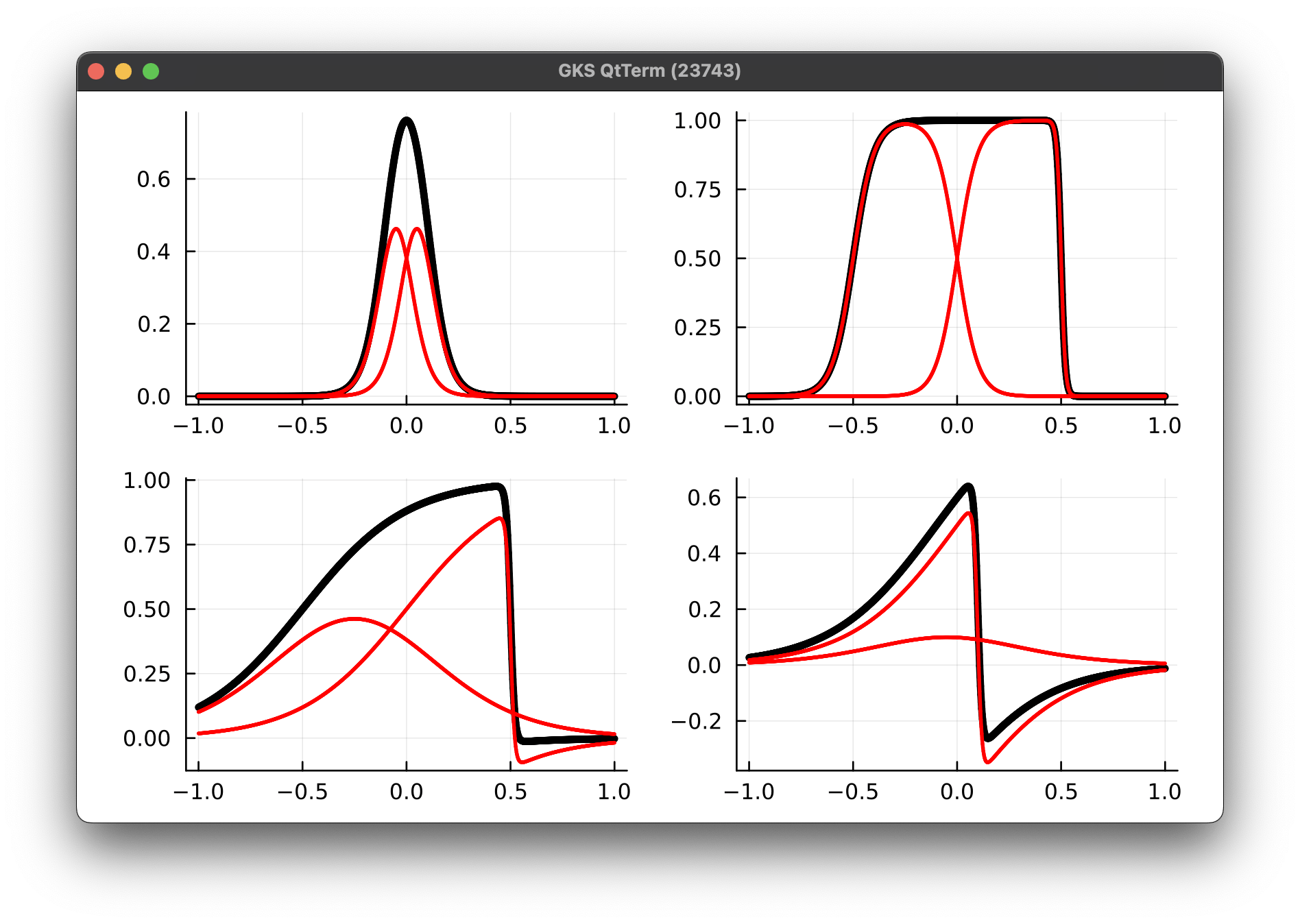

1 Kernel (6 params)
4 Kernel (21 params)