Scientific Peer Review
Cold Diffusion: Inverting Arbitrary Image Transforms Without Noise
DEC 06, 2024
Vedant Puri
https://github.com/vpuri3


Bansal, Arpit, et al. "Cold diffusion: Inverting arbitrary image transforms without noise." Advances in Neural Information Processing Systems 36 (2024).
This paper presents a novel view on diffusion modeling. The diffusion process is viewed as a combination of image degradation and restoration operations, which allows for extending the concept of to arbitrary image transforms that may be deterministic.

1. Summary
Strength: The paper is well written, the presentation is clean, and the ideas are original.
2. Strengths and Weaknesses (1 / 4)
- Diffusion is defined as a combination of an image degradation operation \(D\), and a learned restoration operation \( R_\theta\)
- This generalizes seamlessly to standard diffusion where \(D\) and \(R_\theta\) are noising and denoising
- A transformation agnostic cold sampling scheme (TACoS) is proposed that has first-order error cancellation properties

Song, et al. "Denoising diffusion implicit models."
arXiv preprint arXiv:2010.02502 (2020).
Strength: The experiments are comprehensive and adequately convey the core ideas.
Strength: The proposed sampling scheme is validated against baseline sampling schemes.
Weakness: The sample quality is not substantially better than state of the art image generators.
2. Strengths and Weaknesses (2 / 4)

Image Transform: Deblurring

2. Strengths and Weaknesses (3 / 4)
Image Transform: Super-resolution


Strength: The experiments are comprehensive and adequately convey the core ideas.
Strength: The proposed sampling scheme is validated against baseline sampling schemes.
Weakness: The sample quality is not substantially better than state of the art image generators.
2. Strengths and Weaknesses (4 / 4)
Summary: The approach is original, and the method is technically sound. The exposition is clear with pseudocode provided, and the experiments are conducted on publicly available datasets. Its practical significance is limited because the model does not outperform state of the art diffusion models.
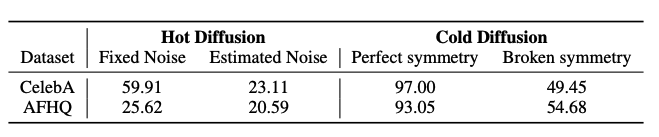
3. Limitations
Compute cost: The computational cost of this paper is lower than a typical diffusion model.
Sample quality: Its practical value is limited due to under-performance against state of the art diffusion models. This limitation is addressed in the paper, and is attributed to the lack of stochasticity in deterministic image transforms leading to a minimal diversity in generated samples.
4. Questions
Q: What are practical limitations of the types of transforms that you can construct diffusion models out of? Must the transform respect the dimension of the image.
Q: Transforms such as blurring or downsampling compress the data-distribution to a low-dimensional subspace. Learning a restoration model may be hard as one fully degraded sample may correspond to many uncorrupted samples. What is the impact on the dimension of the degraded subspace with sample quality? Does the addition of noise in such cases improve sample quality?
Q: Are there problem domains where a deterministic (cold) diffusion model, with minimal diversity in samples, may outperform a stochastic (hot) deterministic model?
5. Ethical concerns
No ethical concerns were identified in this paper. The dataset and code are publicly available.
6. Soundness
Score: 3 (good). The technical claims of this paper are supported by the experimental results, and the experimental methodology is sound.
7. Presentation
Score: 4 (excellent). The ideas in this paper are crisply conveyed without excess jargon. The paper cites relevant literature and places itself in context with recent advances in the field.
8. Contribution
Score: 4 (excellent). This paper marks a substantial contribution to generative modeling field by extending the concept of diffusion modeling to arbitrary image transforms.
9. Overall
Score: 7 (accept). The paper is technically strong with original ideas, and a high impact on the field of diffusion-based generative modeling.
10. Confidence
Score: 5. I am confident in my assessment, and am familiar with related work.