SNF-ROM: Projection-based nonlinear reduced order modeling with smooth neural fields

 

JUL 22, 2024

Vedant Puri, Aviral Prakash, Levent Burak Kara, Yongjie Jessica Zhang

Mechanical Engineering, Carnegie Mellon University

Motivation: accelerate PDE solvers

1

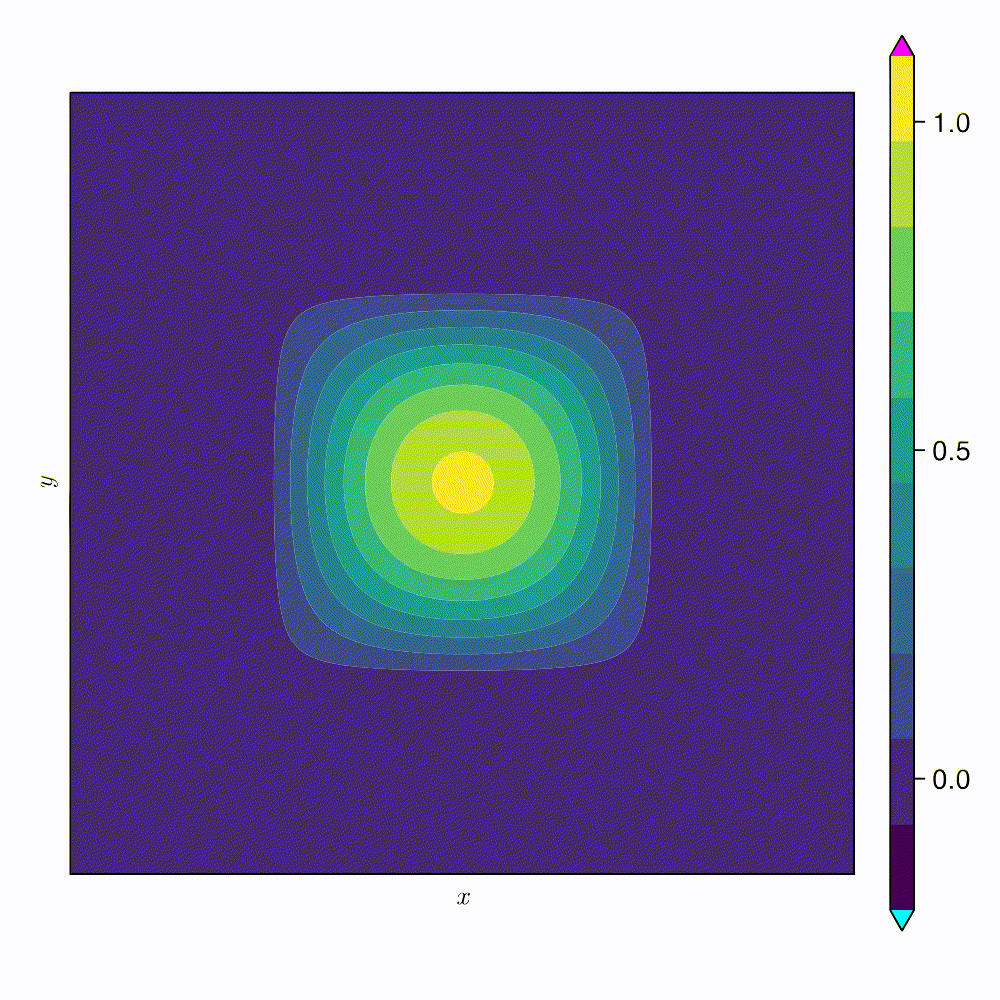
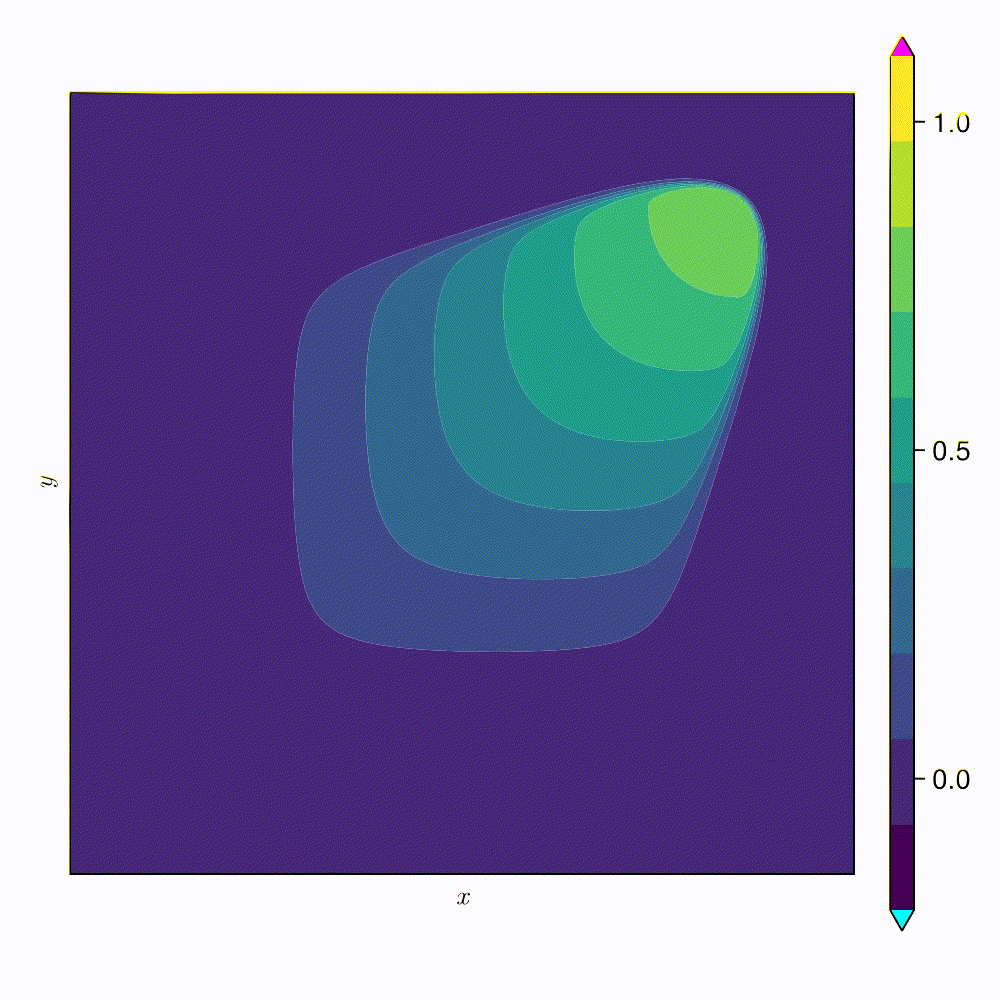
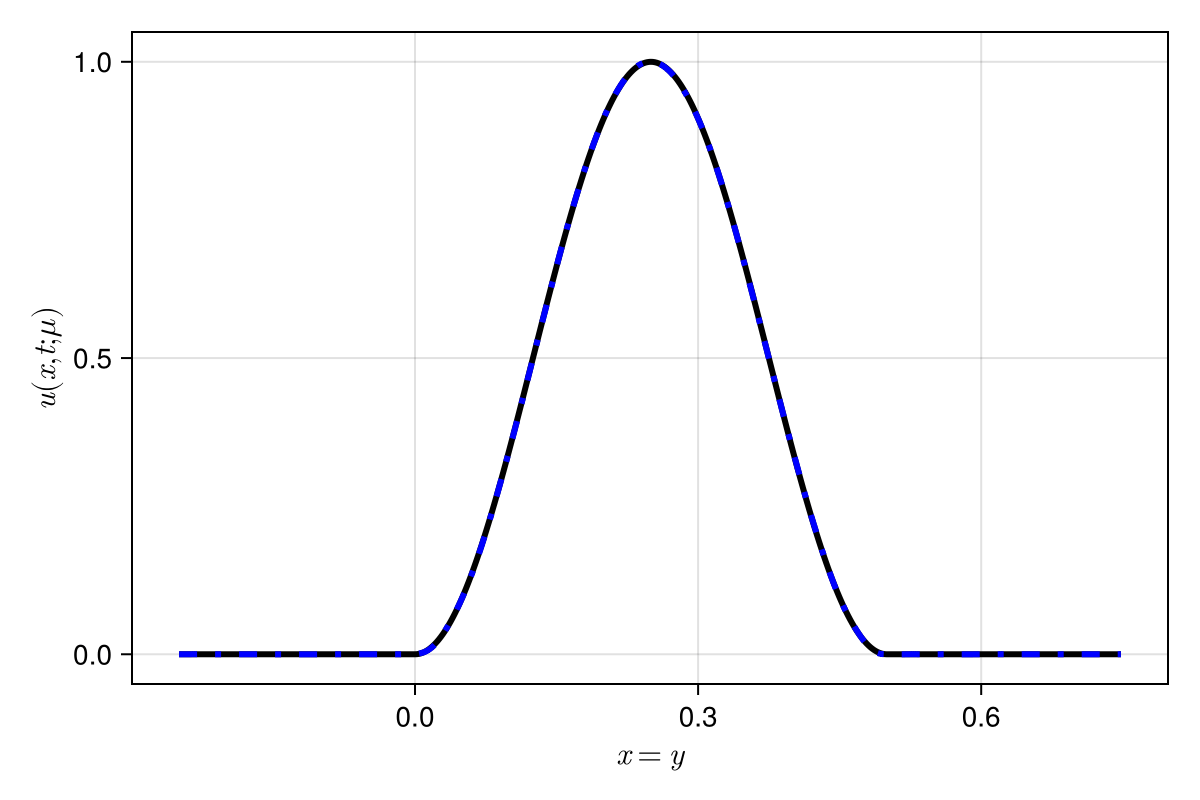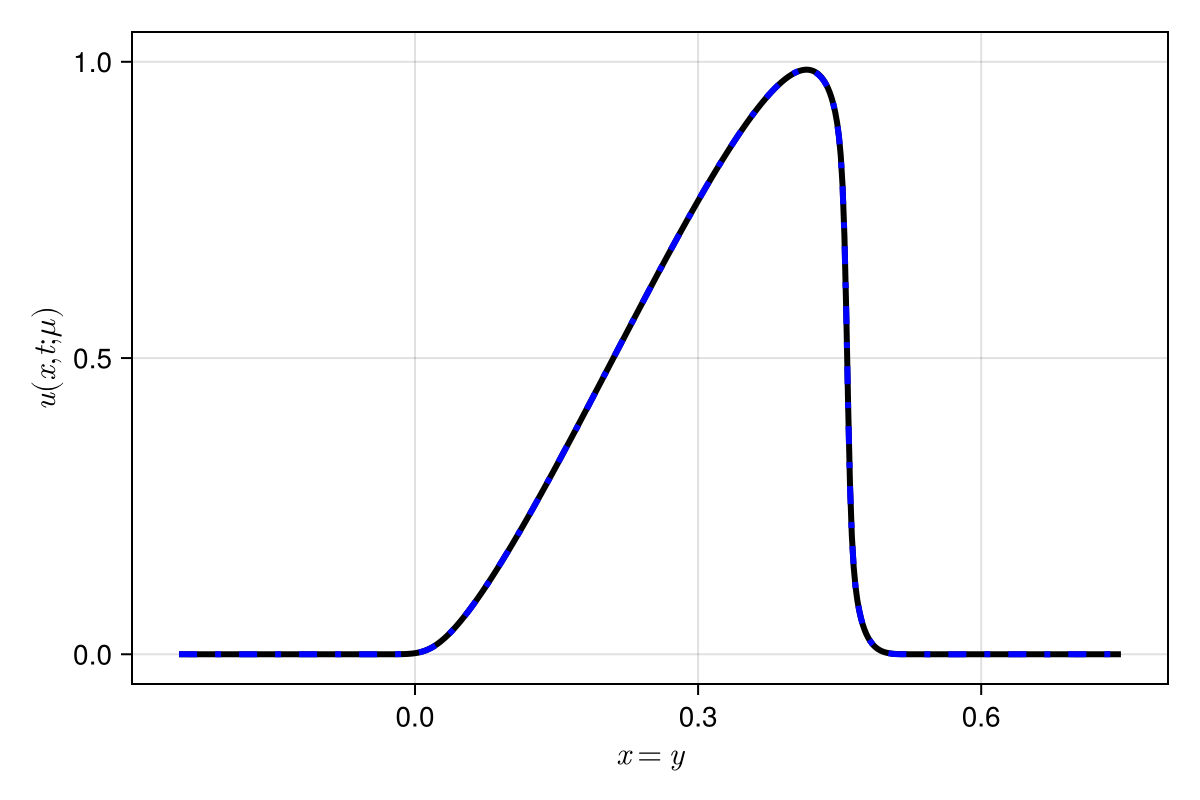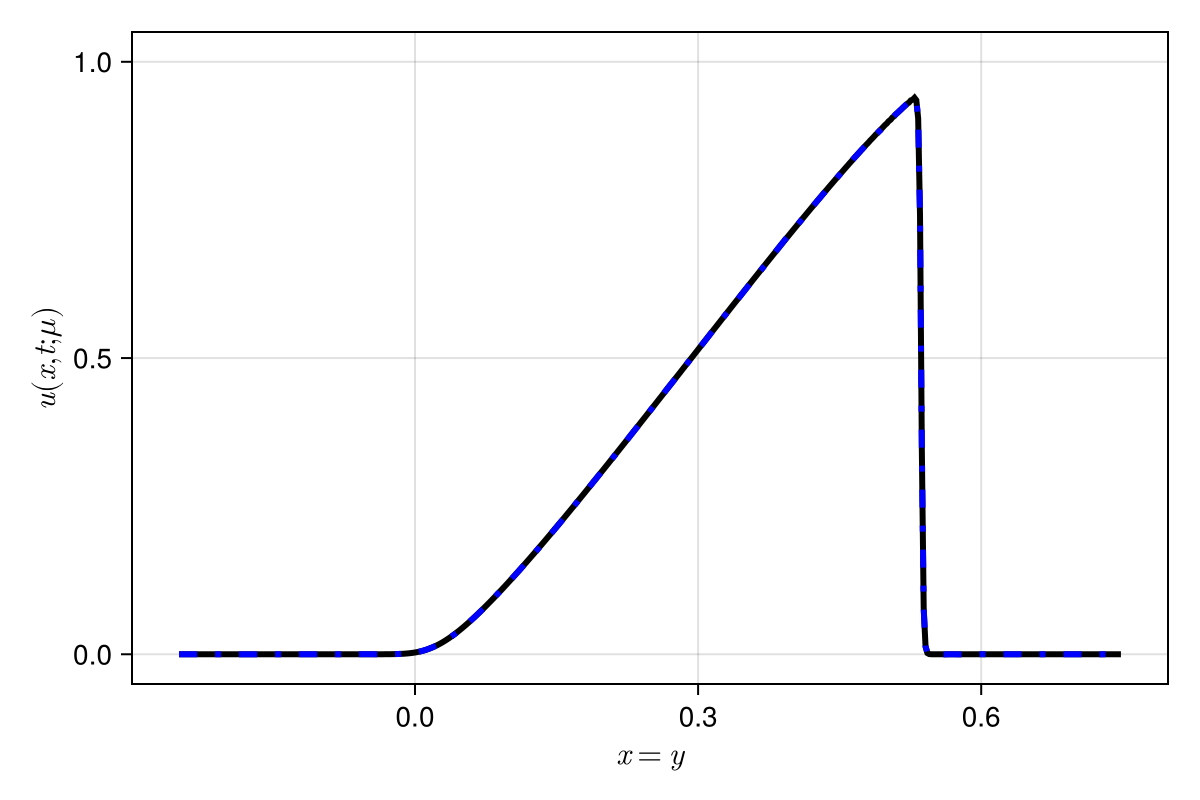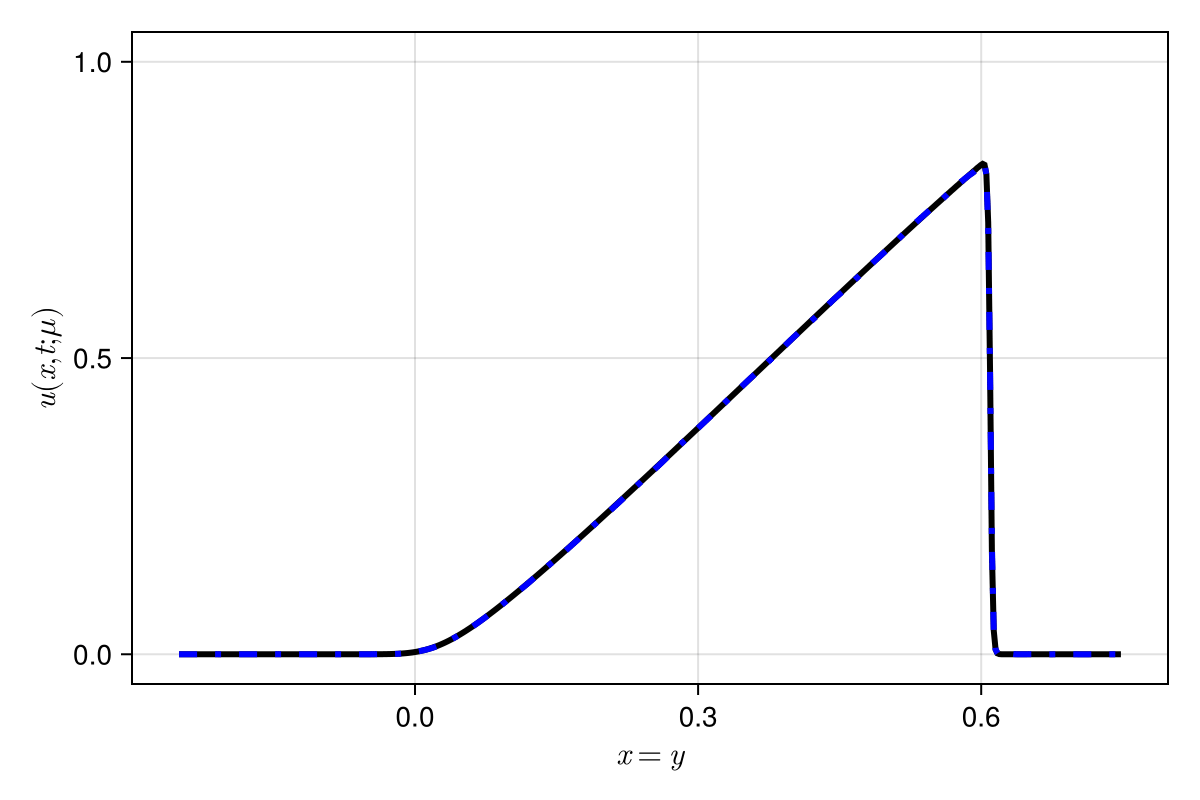
2D Viscous Burgers problem \( (\mathit{Re} = 1\text{k})\)

\frac{\partial \boldsymbol{u}}{\partial t} + \boldsymbol{u} \cdot \boldsymbol{\nabla}\boldsymbol{u} = \nu \Delta \boldsymbol{u}
t=0
t=0.5

Nonlinear model order reduction

  • Spatial discretization that captures the signal with \(2\) DoFs
  • \(0.068~\text{s}\) wall-time, \(261~\text{MiB}\) GPU allocation
  • \(199\times\) speed-up, \(0.37\%\) relative error

Full order model (FOM)

  • Fourier spectral PDE solver
  • \(512 \times 512\) grid \( (\approx 262~\text{k}) \) grid points
  • \(13.44~\text{s}\) wall-time, \(640~\text{GiB}\) GPU allocation

Model order reduction learns data-driven spatial discretizations

2

\begin{pmatrix} \hspace{0.8em} \\ \\ \\ \\ \end{pmatrix}
\begin{pmatrix} \hspace{0.8em} \\ \\ \\ \\ \end{pmatrix}
\mathbb{R}^{N_\text{FOM}}
\bar{u}(0)
\bar{u}(T)
\text{Full-order model (FOM) solves an ODE of size } \mathcal{O}(N_\text{FOM})
\text{Linear ROMs project the governing ODE to a linear subspace}
\text{Nonlinear ROMs project the ODE onto a low-dimensional nonlinear manifold}
\frac{\partial \boldsymbol{u}}{\partial t} = \mathcal{L}(\boldsymbol{x}, t, \boldsymbol{u})
\implies \frac{\mathrm{d}\bar{u}}{\mathrm{d} t} = \mathcal{L}(t, \bar{u})

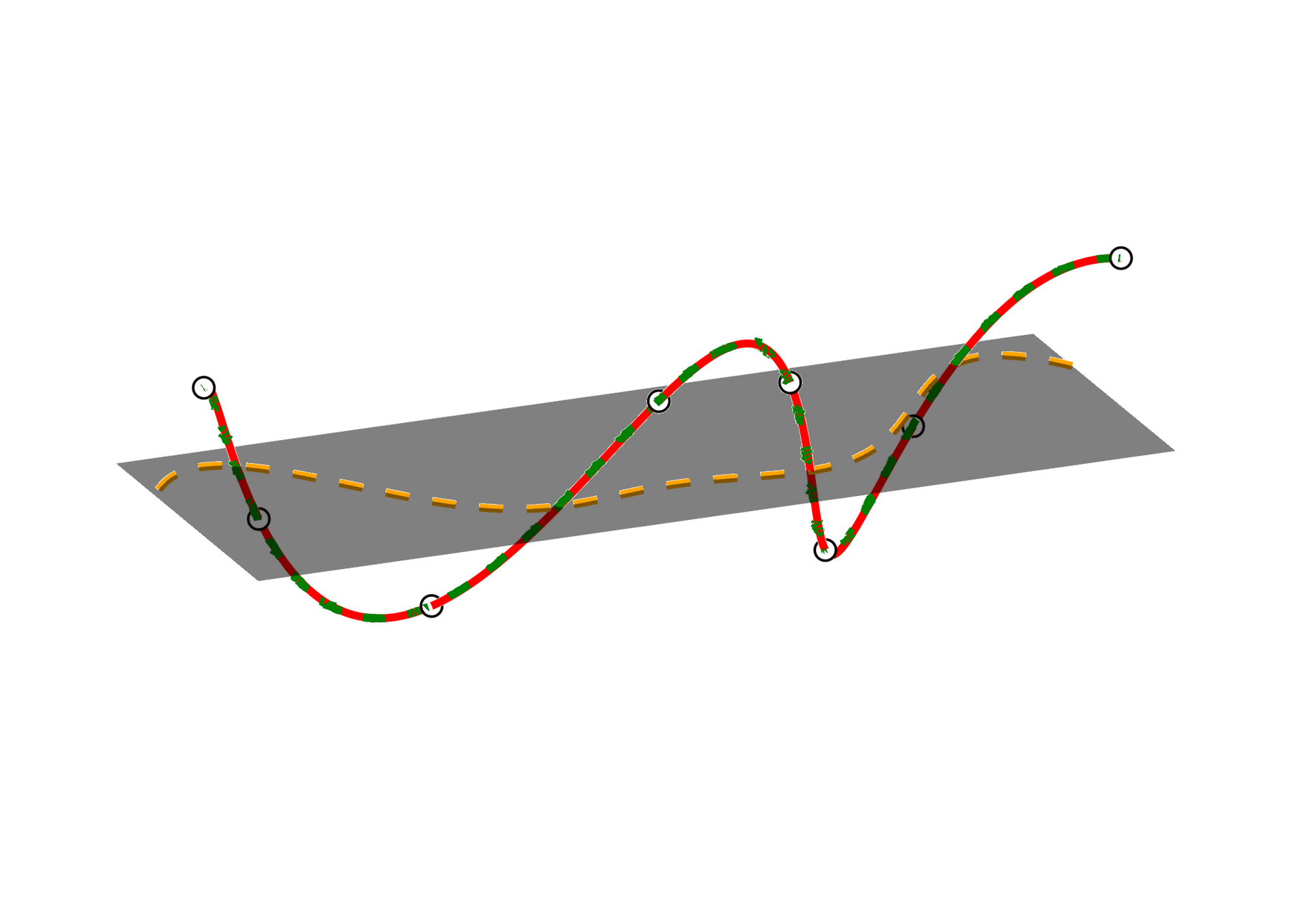
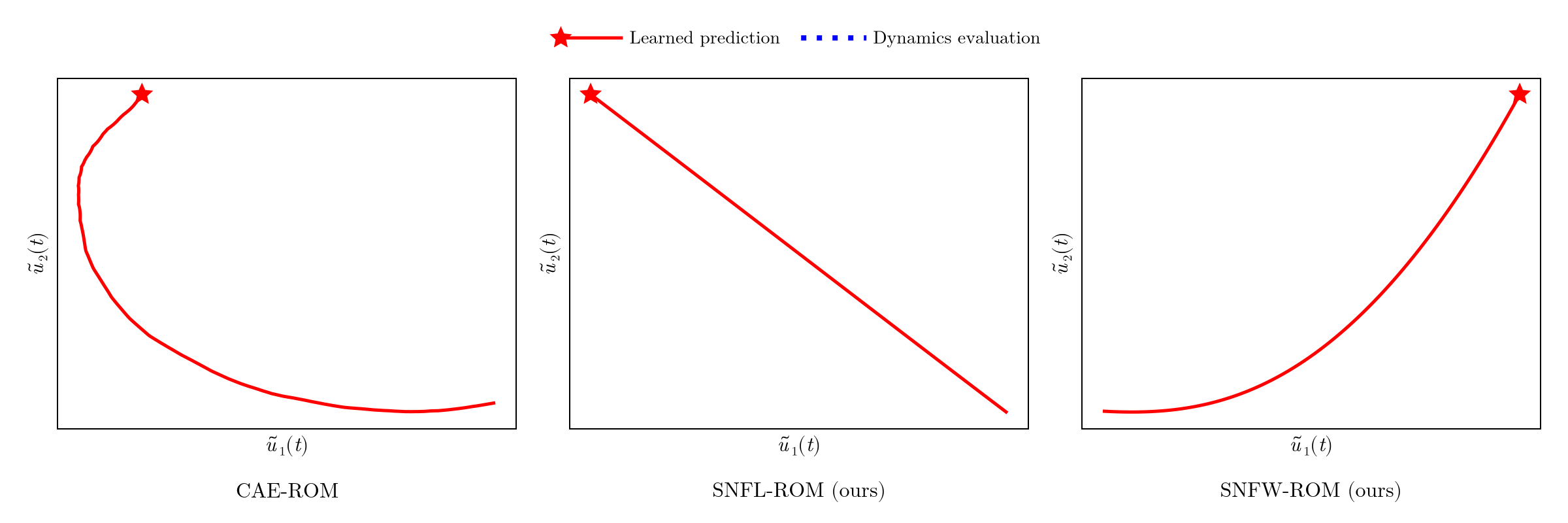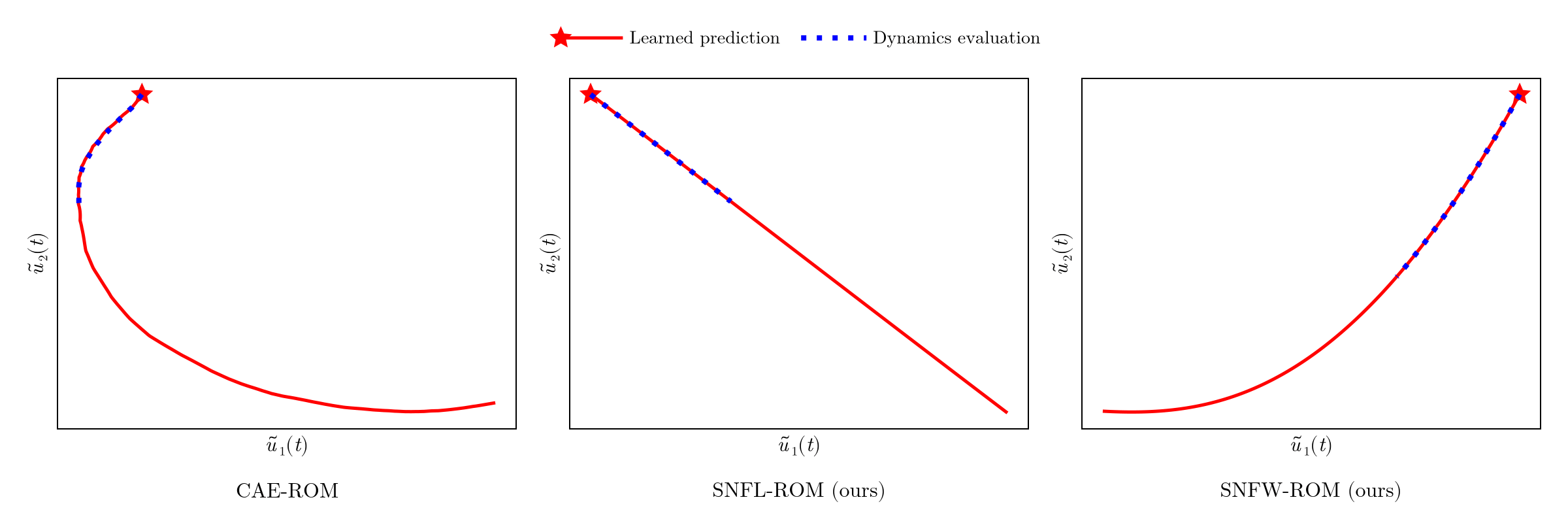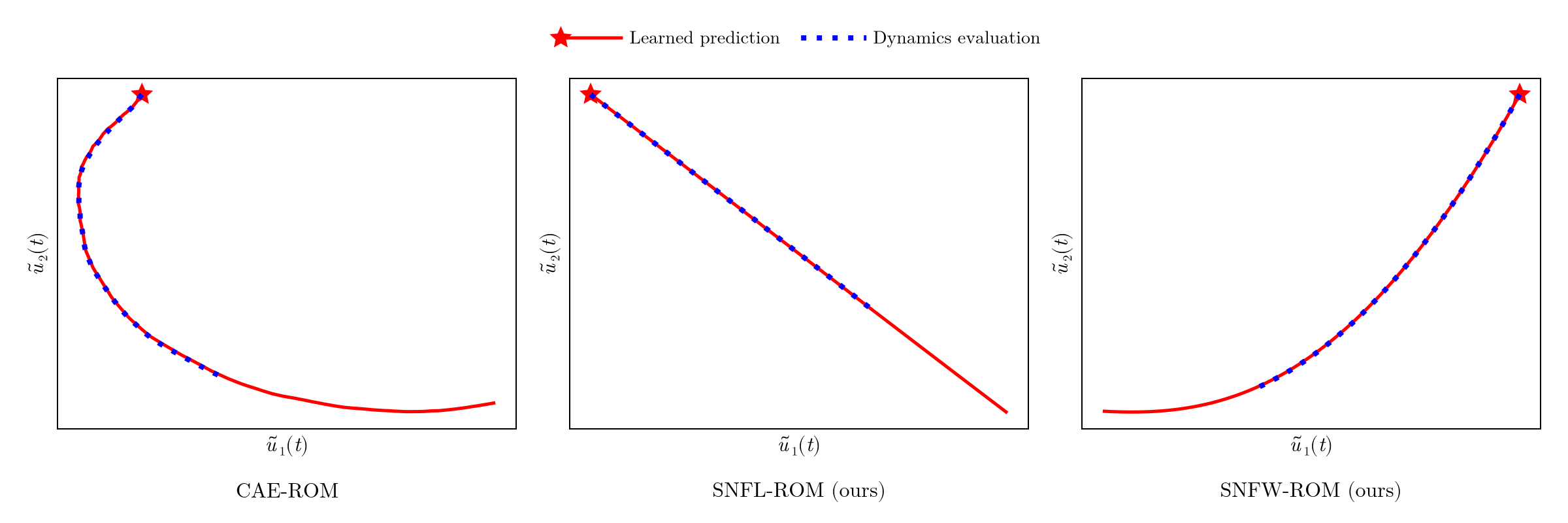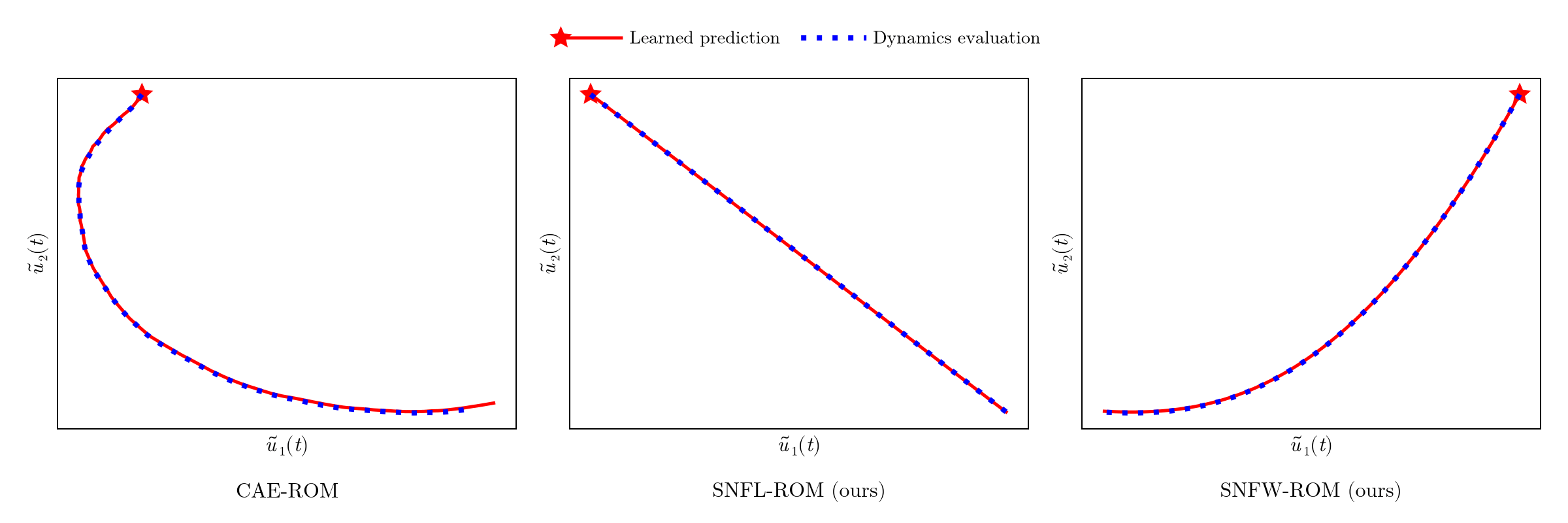
Convolutional autoencoder ROMs (CAE-ROMs)

4

\begin{pmatrix} \textcolor{blue}*\\ \textcolor{blue}*\\ \end{pmatrix}
\begin{pmatrix} \hspace{0.8em} \\ \\ \\ \\ \end{pmatrix}
\begin{pmatrix} \hspace{0.8em} \\ \\ \\ \\ \end{pmatrix}
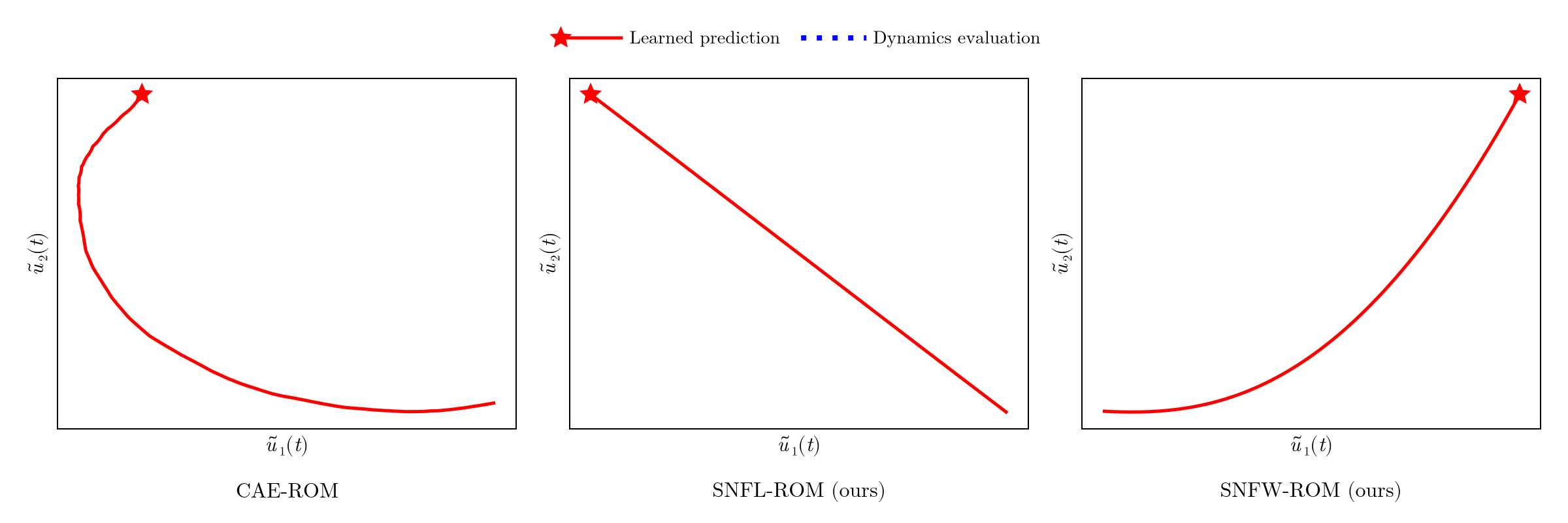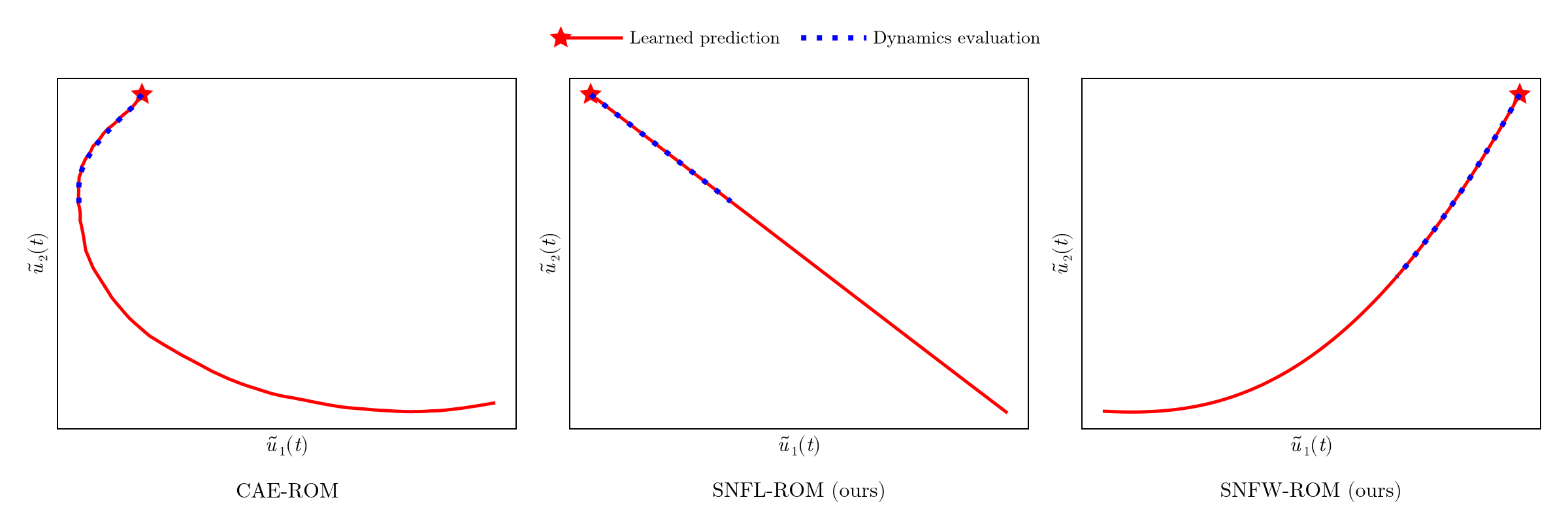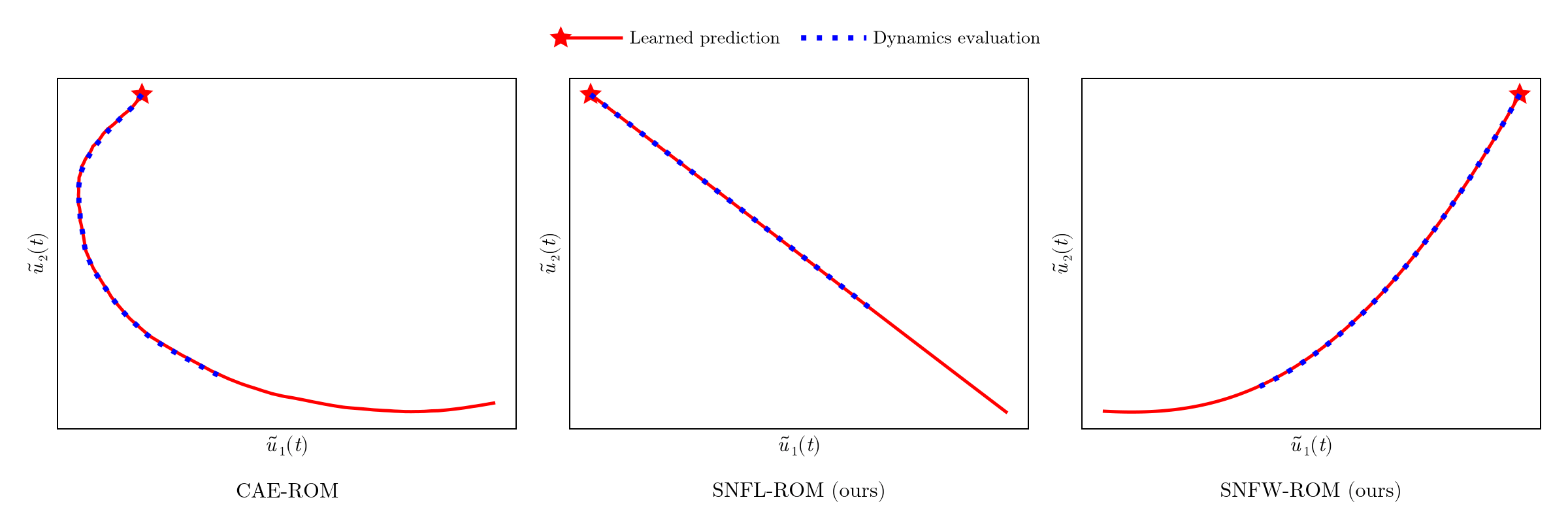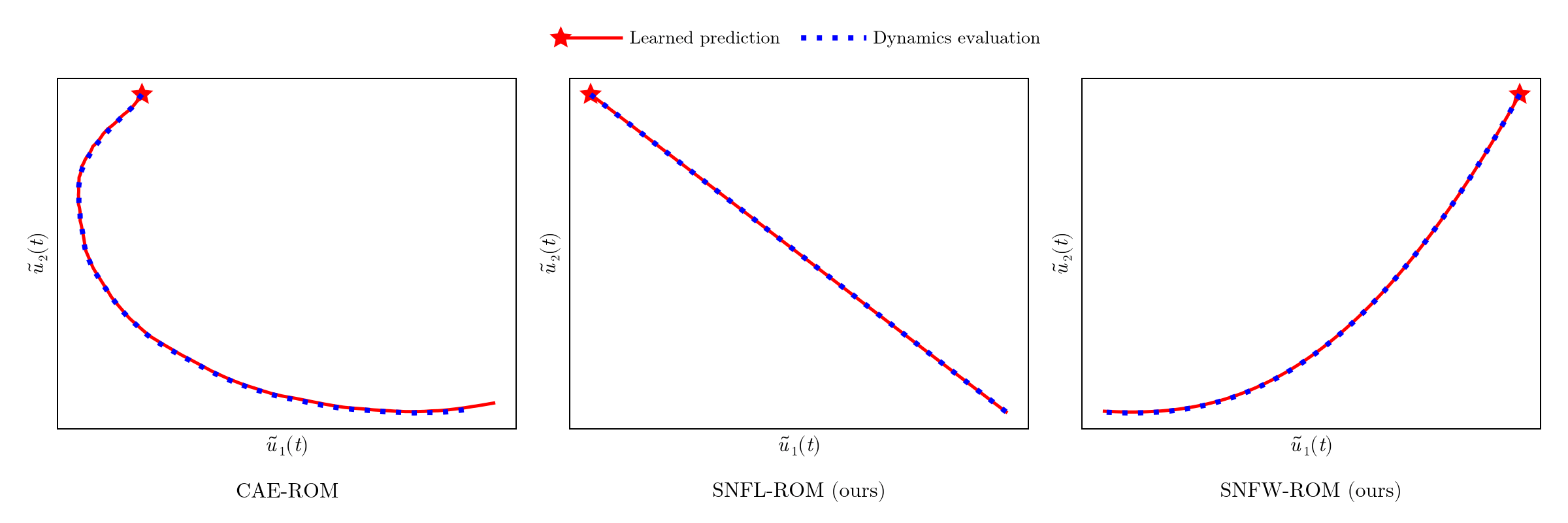
  • Unsupervised learning technique for data compression
  • No control over latent trajectory of ROM DoFs
  • ROM dynamics evaluation deviates from learned prediction
\text{Relative error vs time}
\text{Predictions}
\text{Distribution of ROM states}
\text{Encoder}
\text{Decoder}
\bar{u}(t)
\bar{u}(t)
\tilde{u}(t)

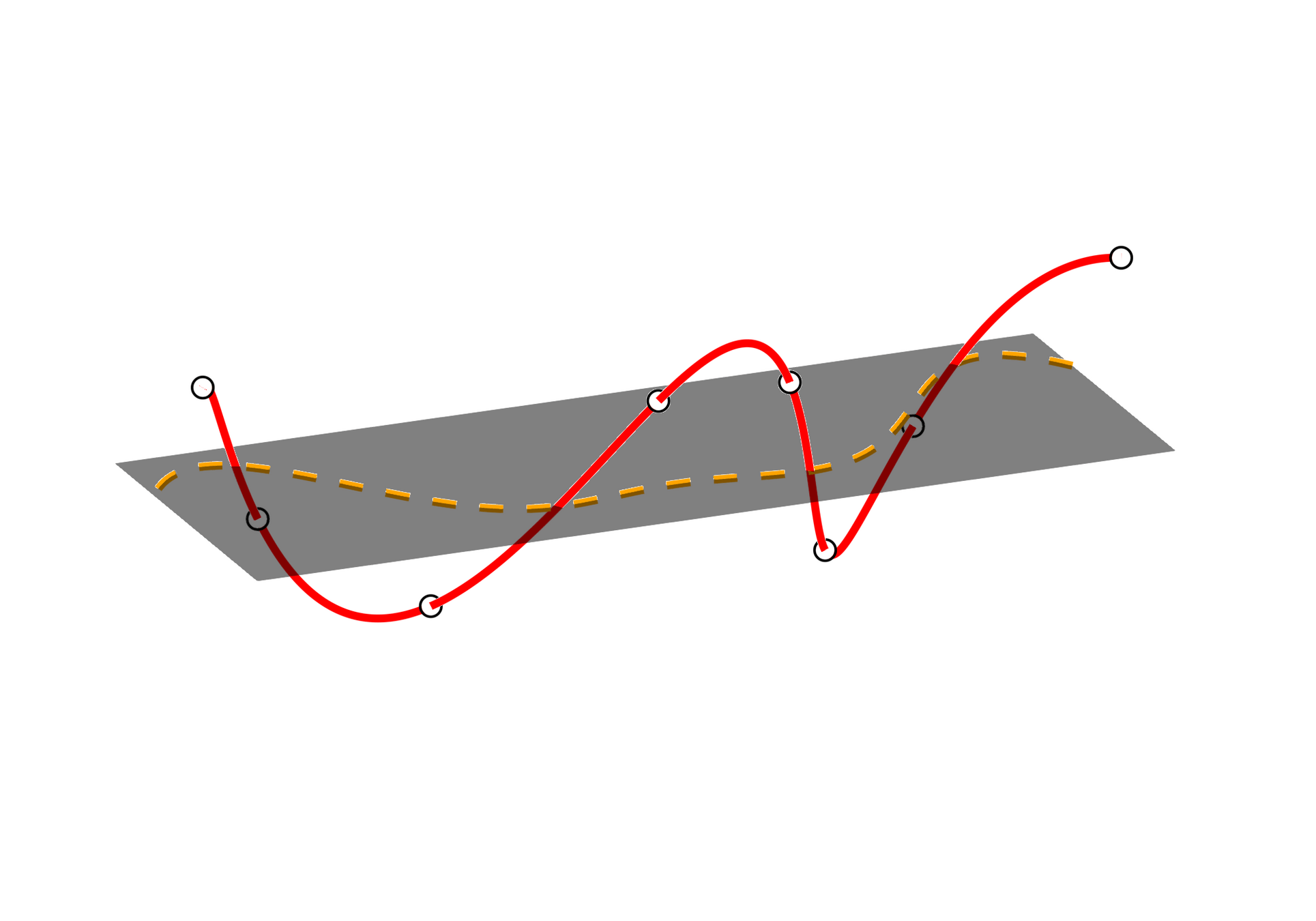
SNF architecture: directly model the intrinsic ROM manifold

5

\(\text{Coordinates}\)

\(\text{Loss } (L)\)

\(\text{PDE Problem}\)

\((\boldsymbol{x}, t, \boldsymbol{\mu})\)

\(\text{ Parameters}\)

\( \text{and time}\)

\(\text{Smooth neural field MLP }(g_\theta)\)

\(\text{Backpropagation}\)

\(\text{ Intrinsic ROM manifold}\)

\(\tilde{u}\)

\(\boldsymbol{x}\)

\(\boldsymbol{u}\left( \boldsymbol{x}, t; \boldsymbol{\mu} \right)\)

\(\mathcal{\tilde{U}}\)

\(\nabla_\theta L\)

\(\nabla_\varrho L\)

\(\nabla_\theta L\)

Modeling \(\tilde{\mathcal{U}}\) as a learnable function \(\Xi_\varrho\) restricts ROM states to follow a smooth trajectory.

\tilde{\mathcal{U}} = \left\{ \tilde{u}(t; \mathbf{\mu}) |~ t,\, \mathbf{\mu} \right\}

Neural field are ill-equipped to handle high-order derivatives

8

  • Grid independent. easy implementation of hyper-reduction
  • Problem: inaccurate high-order derivatives

\(\text{Neural field MLP } (g_\theta)\)

\(\boldsymbol{x}\)

\(\boldsymbol{u}\left( \boldsymbol{x} \right)\)

\frac{\mathrm{d}}{\mathrm{d}x} \mathrm{NN}(x)
\mathrm{NN}(x)
\frac{\mathrm{d}^2}{\mathrm{d}x^2} \mathrm{NN}(x)
\dfrac{\mathrm{d}^k}{\mathrm{d}x^k} \mathrm{NN}(x) \neq u^{(k)}(x)

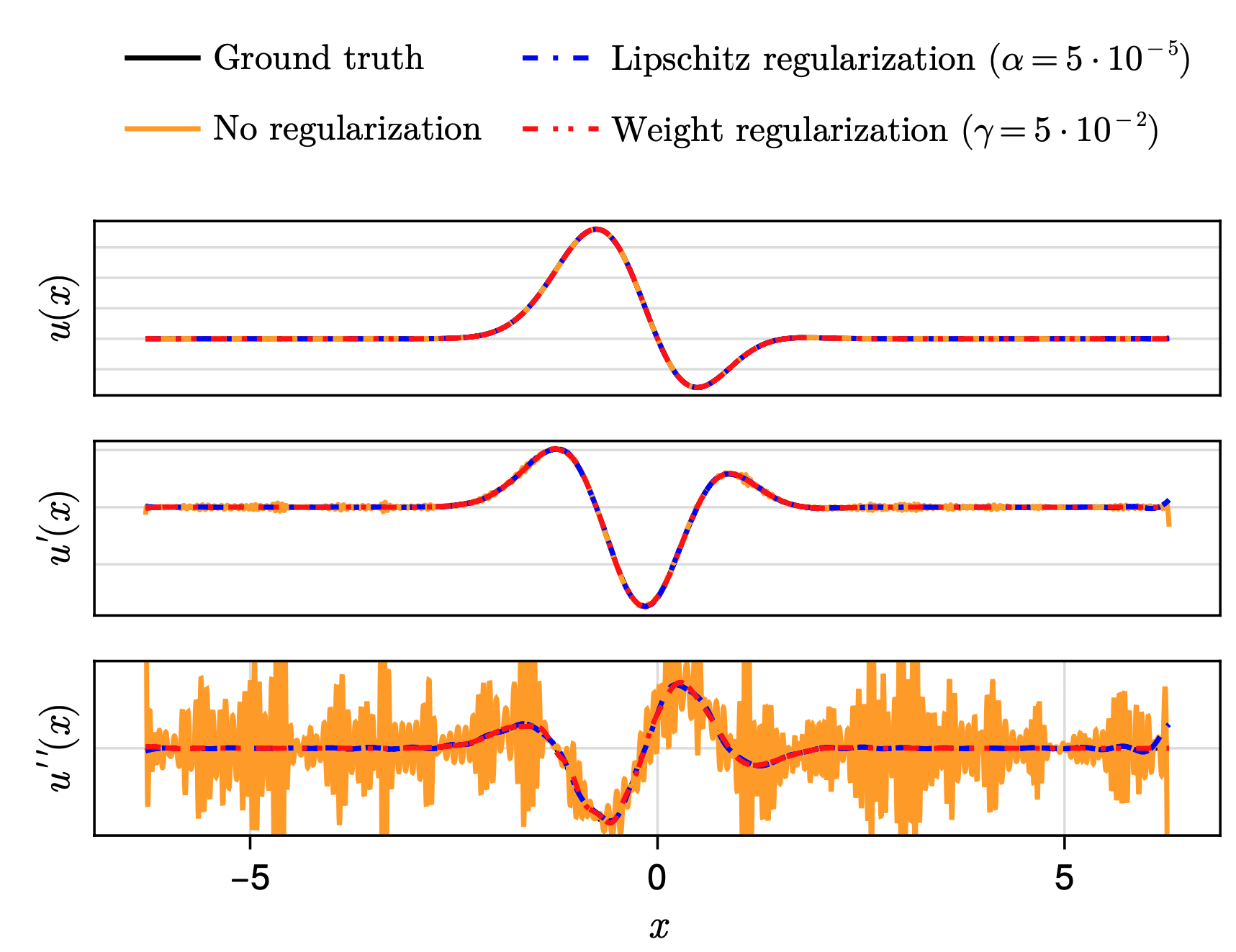
Solution: Apply regularization to ensure that the learned neural field is inherently smooth

  • Lipschitz regularization penalizes the Lipschitz constant of the MLP
  • Weight regularization penalizes high-frequency components in \( \dfrac{\mathrm{d}}{\mathrm{d}x}\mathrm{NN}(x)\)

Dynamics evaluation with Galerkin projection

3

\bar{u}(t=0)
\tilde{u}(t=0)
\tilde{u}(t=T)
\bar{u}(t=T)
\mathbb{R}^{N_\text{FOM}}
\bar{u}(0)
\tilde{u}(0)
\tilde{u}(T)
\mathcal{M}
\bar{u}(T)
h_\text{ROM}
g_\text{ROM}
\text{Manifold}\\ \text{projection}
\text{Model}\\ \text{inference}
\frac{\mathrm{d} \bar{u}}{\mathrm{d} t} = \mathcal{L}(\bar{u}, t)
\mathbf{J}_g\frac{\mathrm{d} \tilde{u}}{\mathrm{d} t} = \mathcal{L}(g_\text{ROM}(\tilde{u}), t)
\text{FOM evaluation: } \mathcal{O}(N_\text{FOM})
\text{ROM evaluation: } \mathcal{O}(N_\text{ROM})
\begin{pmatrix} \hspace{0.4em} \\ \\ \end{pmatrix}
\begin{pmatrix} \hspace{0.4em} \\ \\ \end{pmatrix}

Experiment: 2D viscous Burgers problem \( (\mathit{Re} = 1\mathrm{k})\)

6

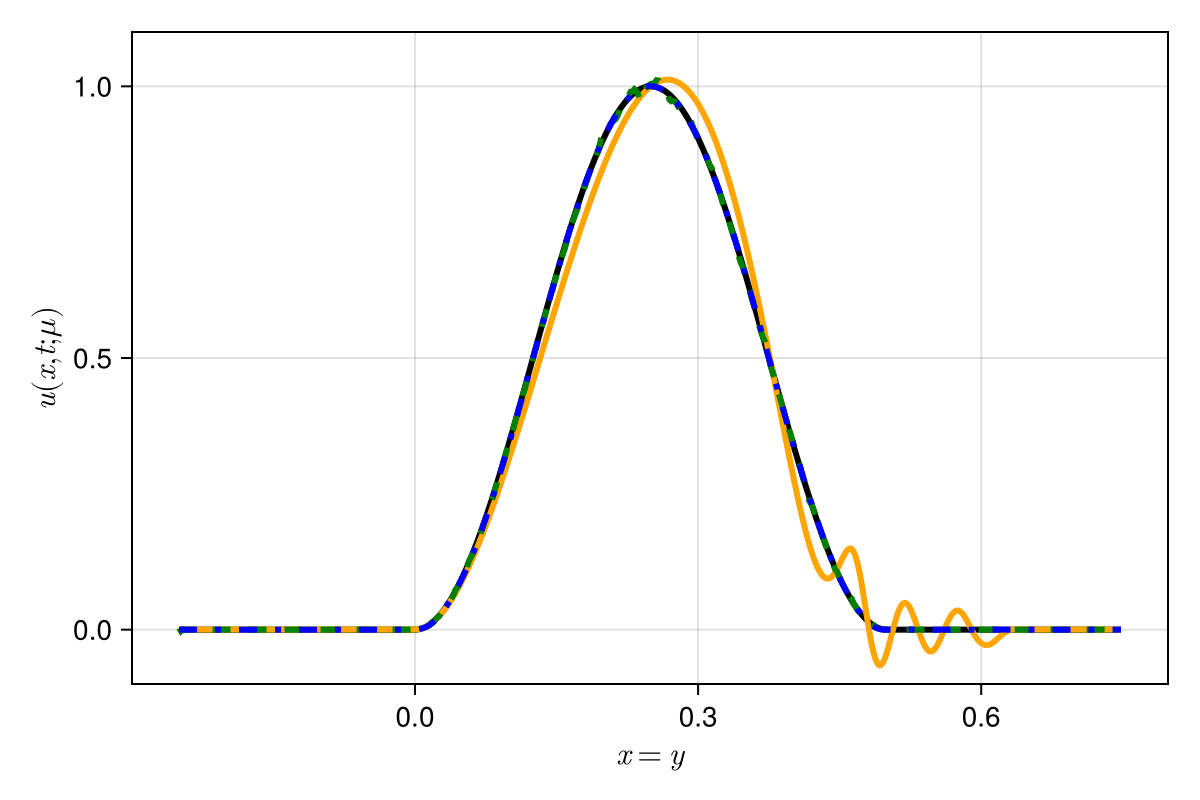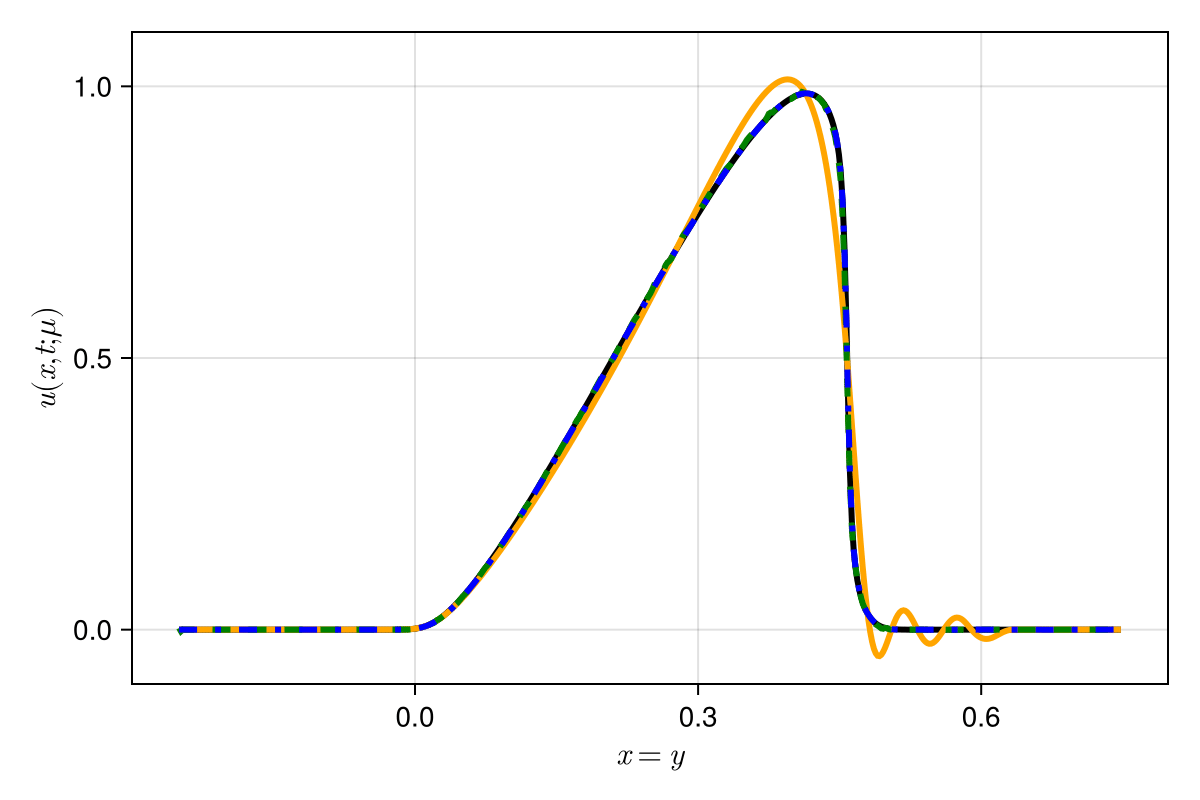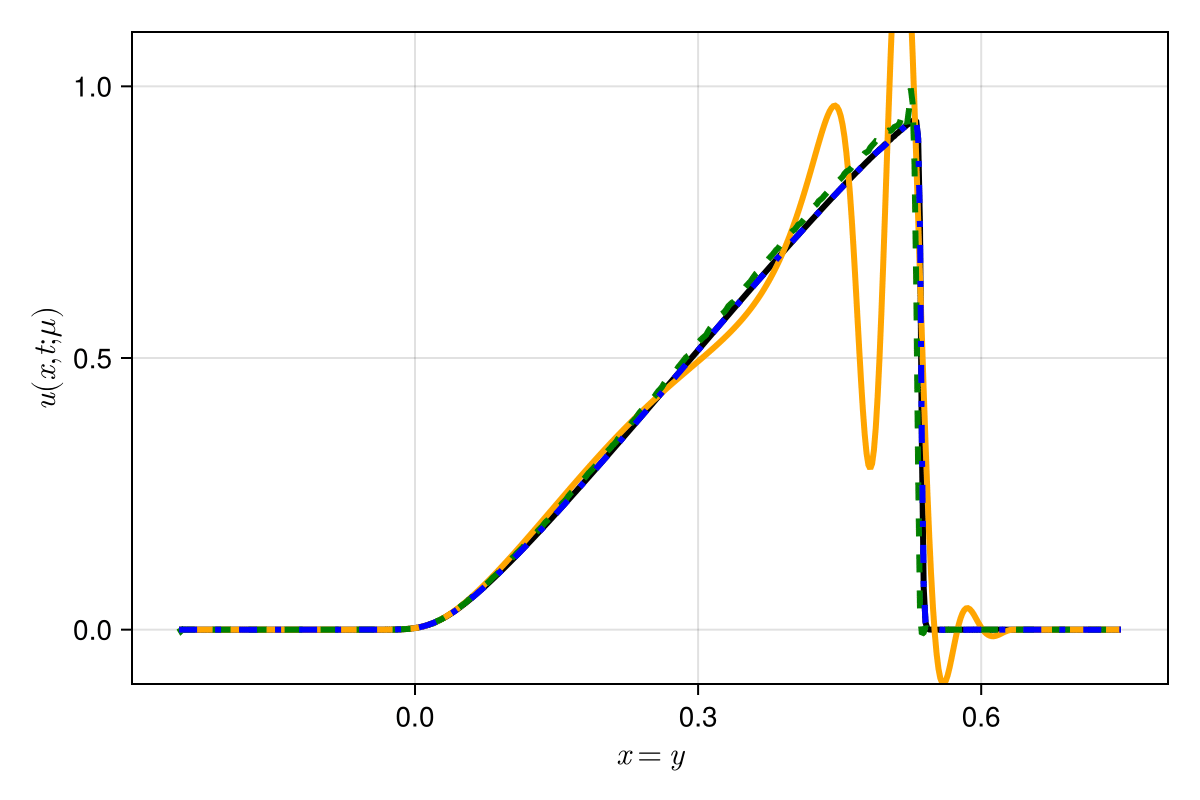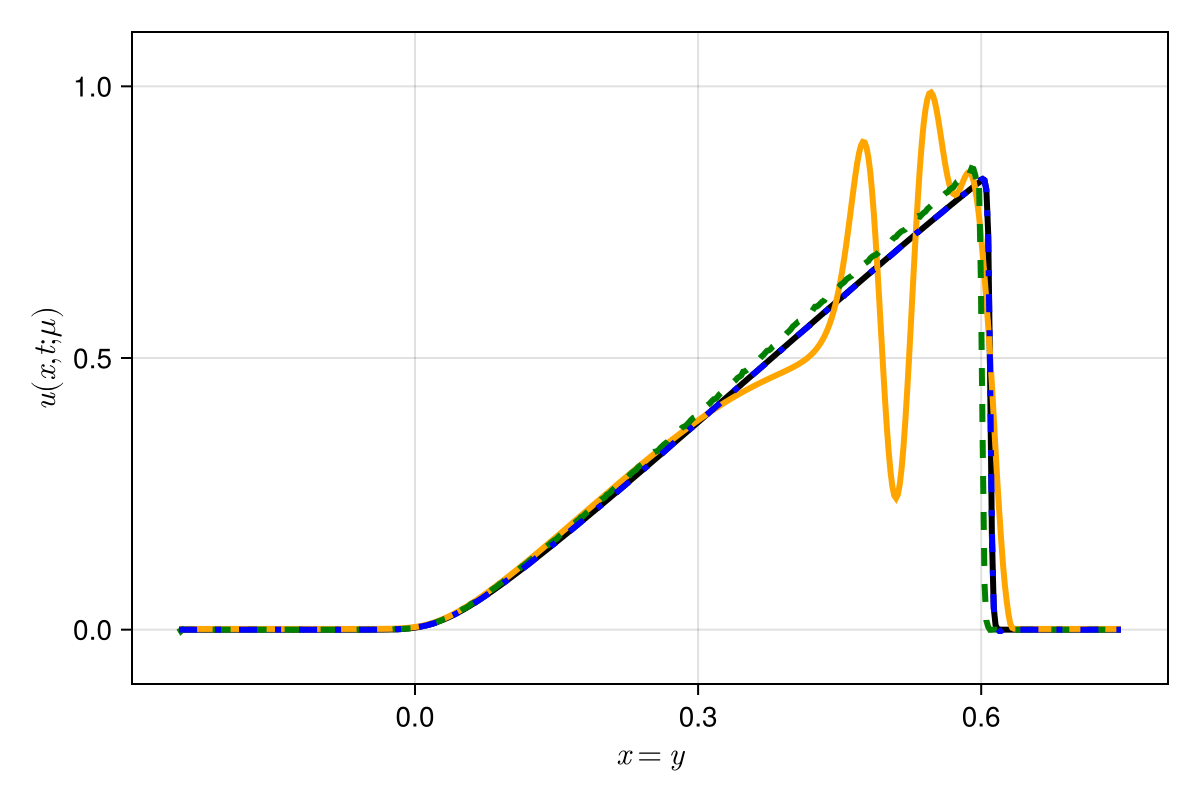
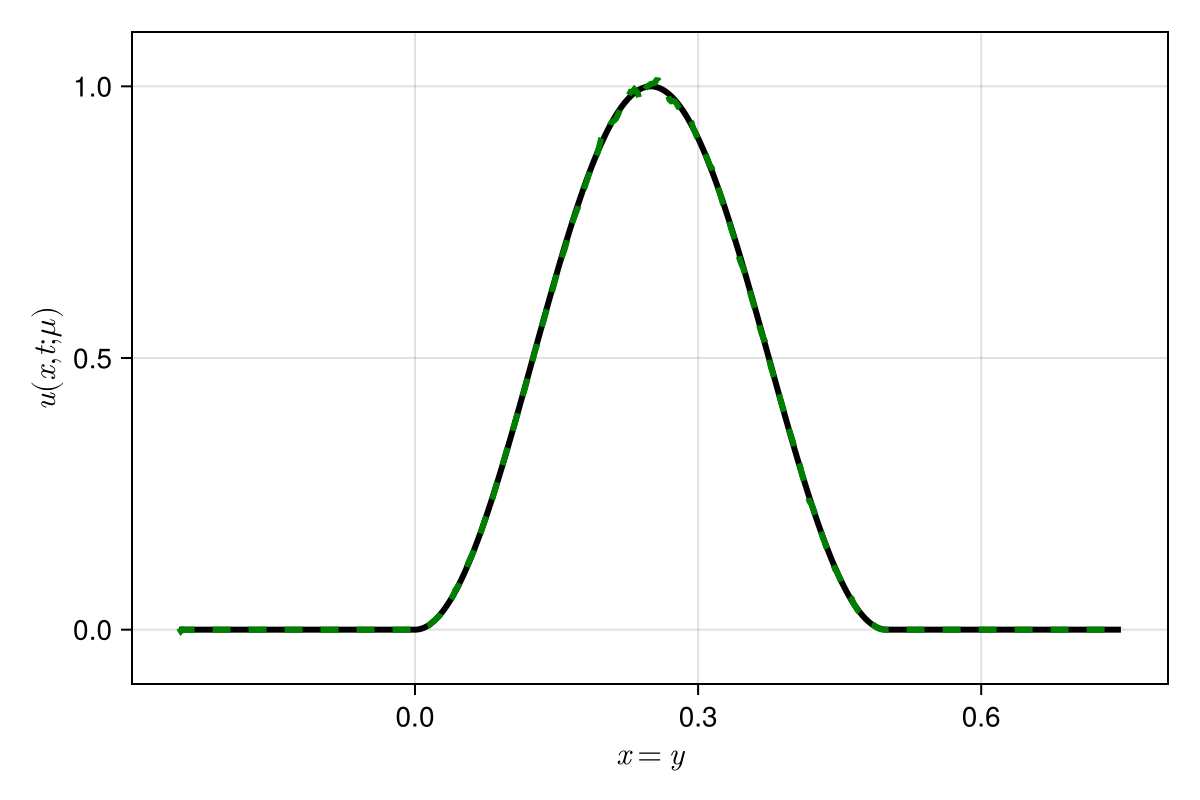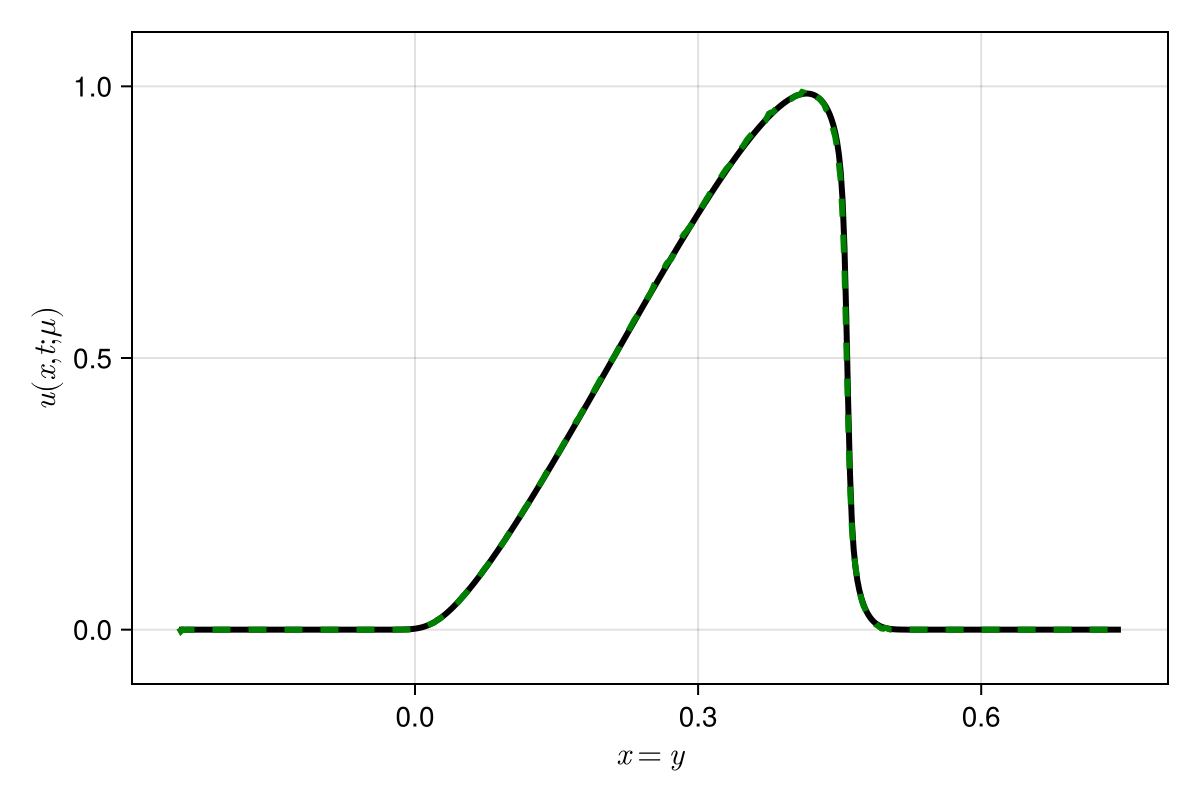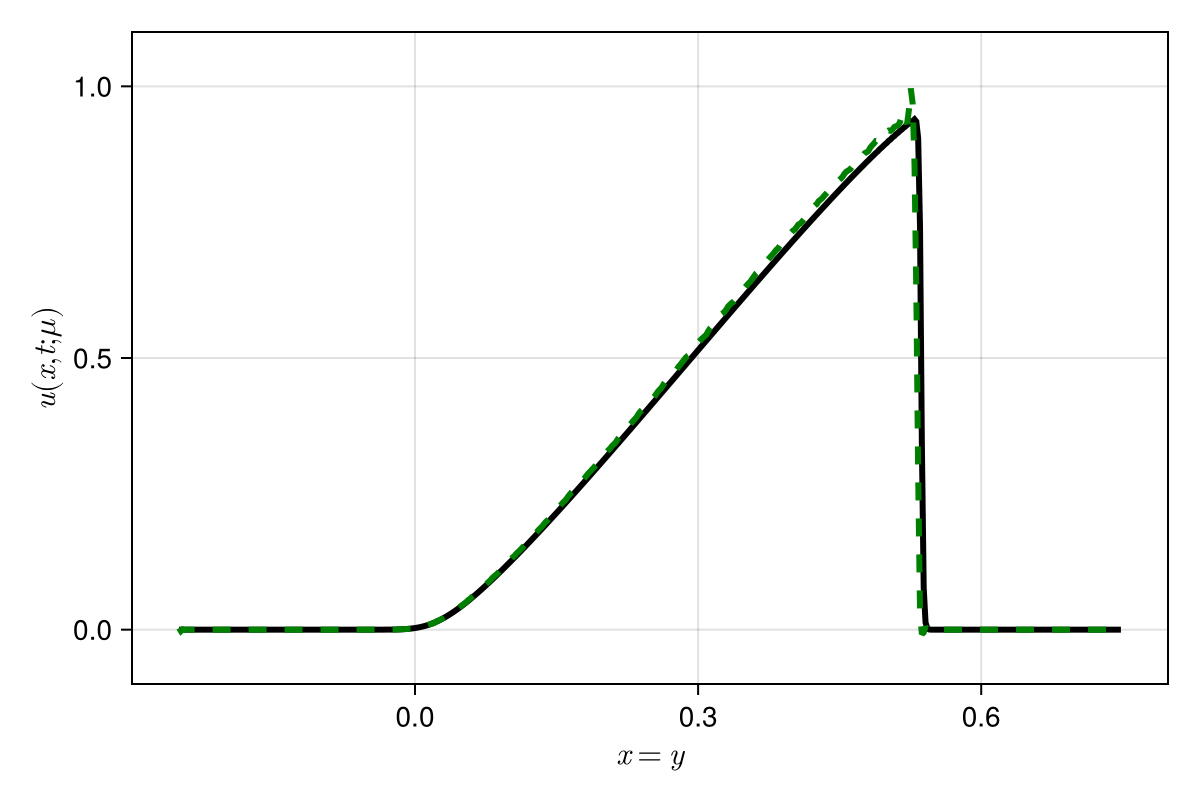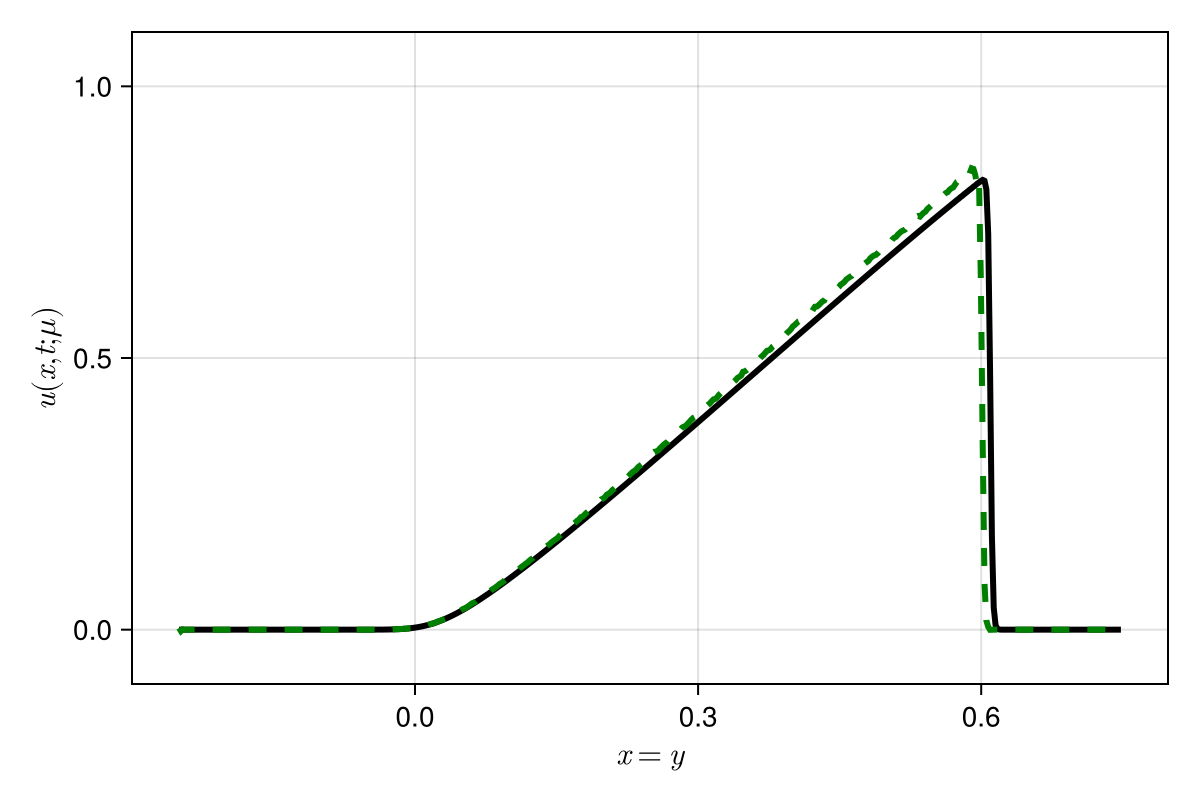
Experiment: 1D scalar advection problem

7

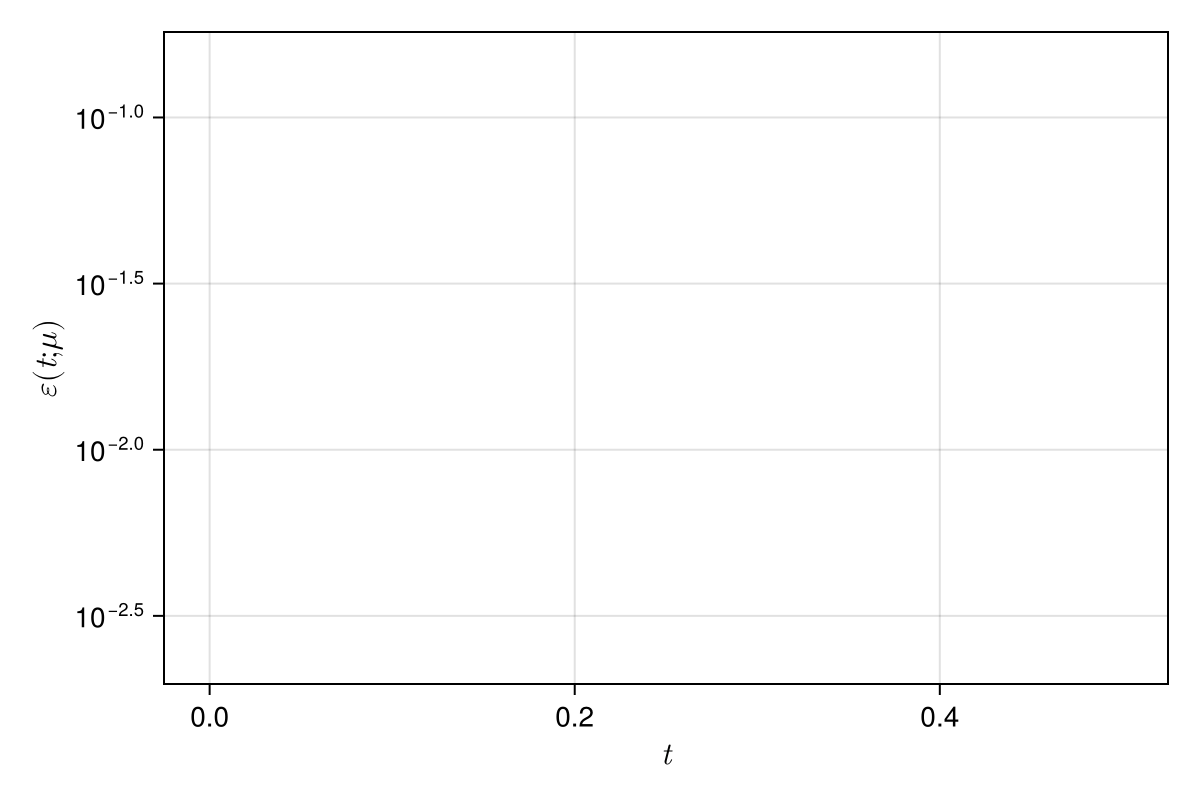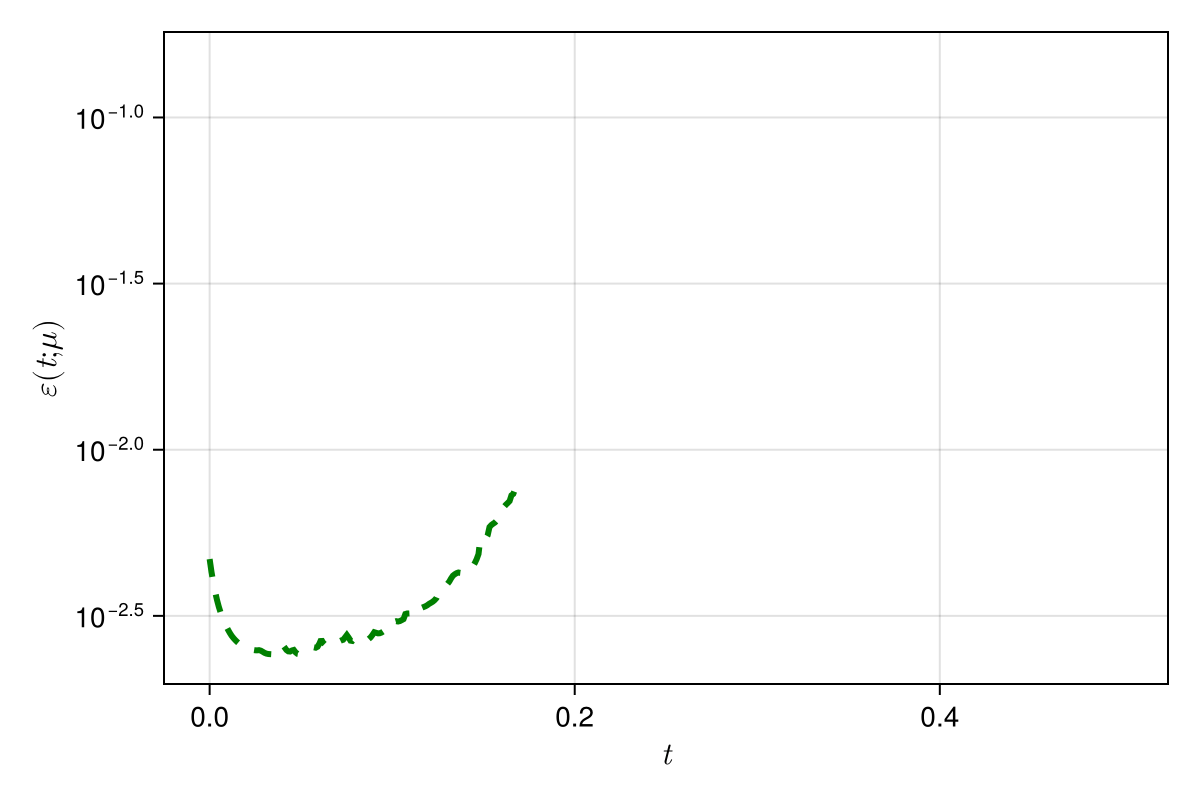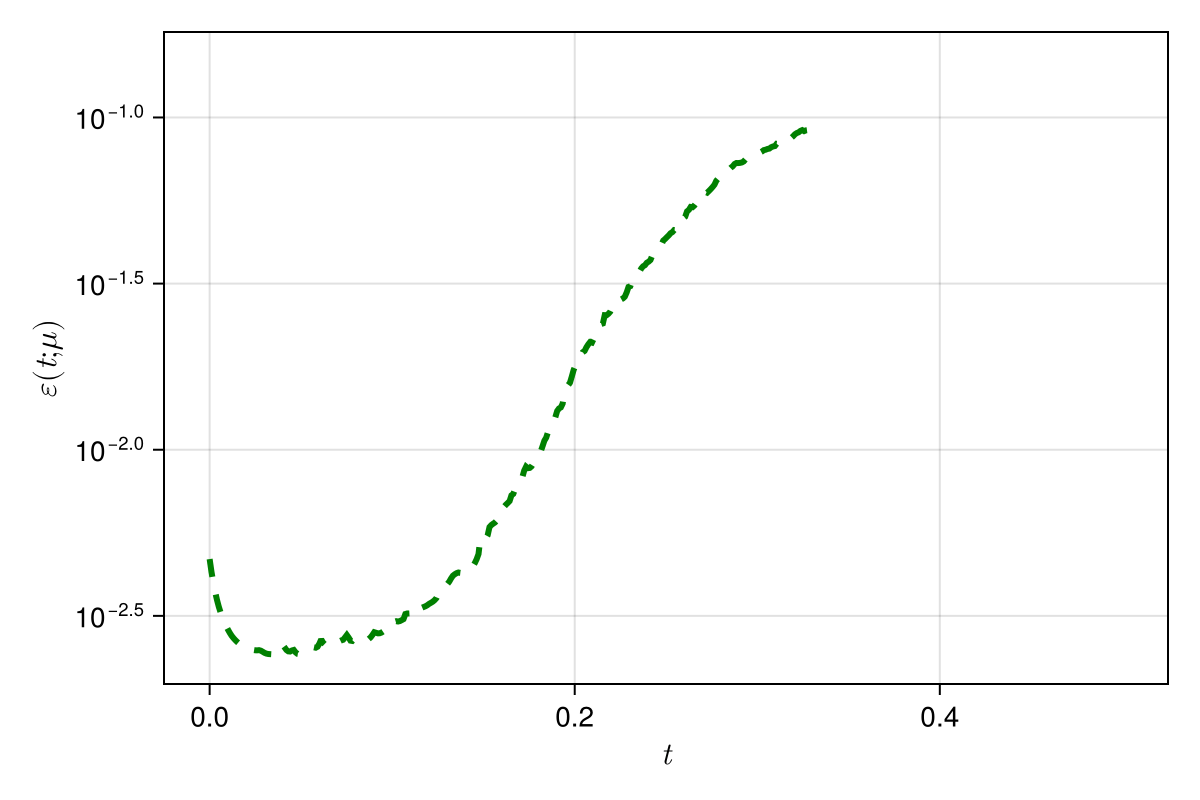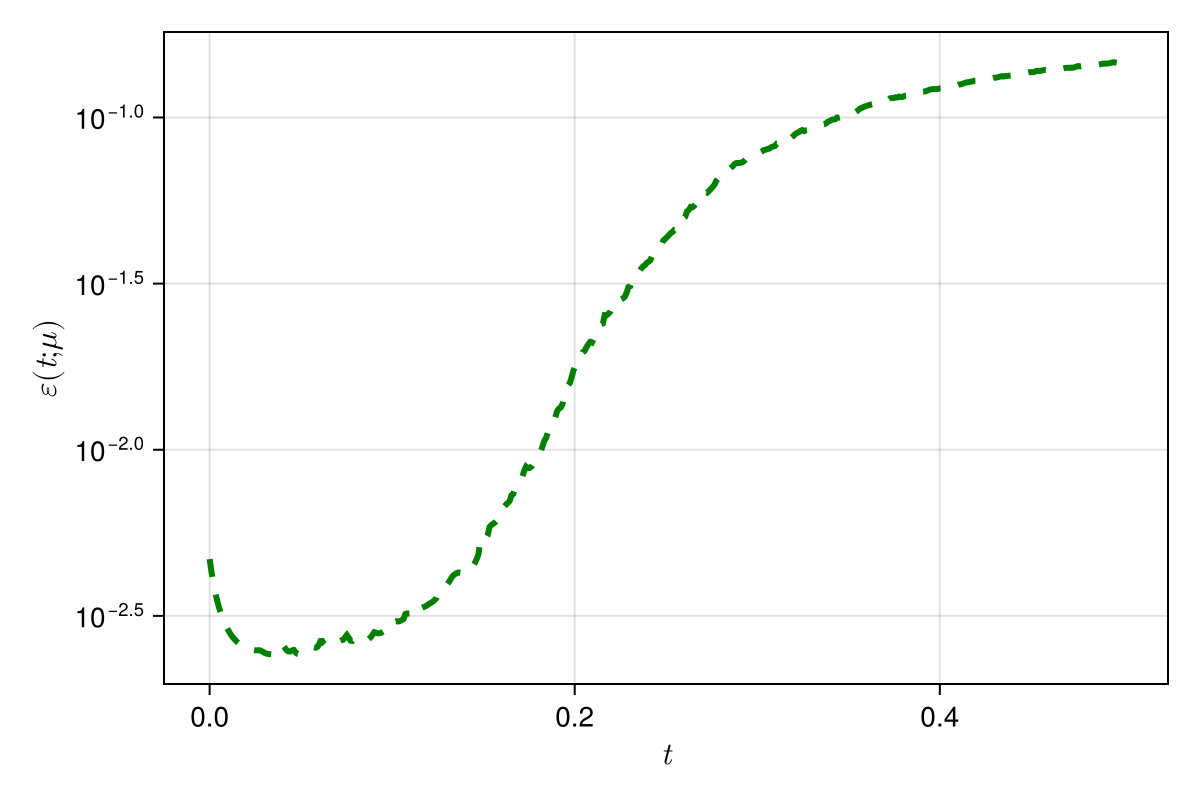
Smooth trajectory of ROM states allows for taking larger time-steps without sacrificing accuracy

\(\text{Predictions}\)

\(\text{Relative error } (\Delta t = \Delta t_0)\)

\(\text{Relative error } (\Delta t = 10\Delta t_0)\)

\(\text{CAE-ROM}\)

\(\text{SNFL-ROM}\)

\(\text{SNFW-ROM}\)

Experiment: 1D Kuramoto-Sivashinsky problem

9

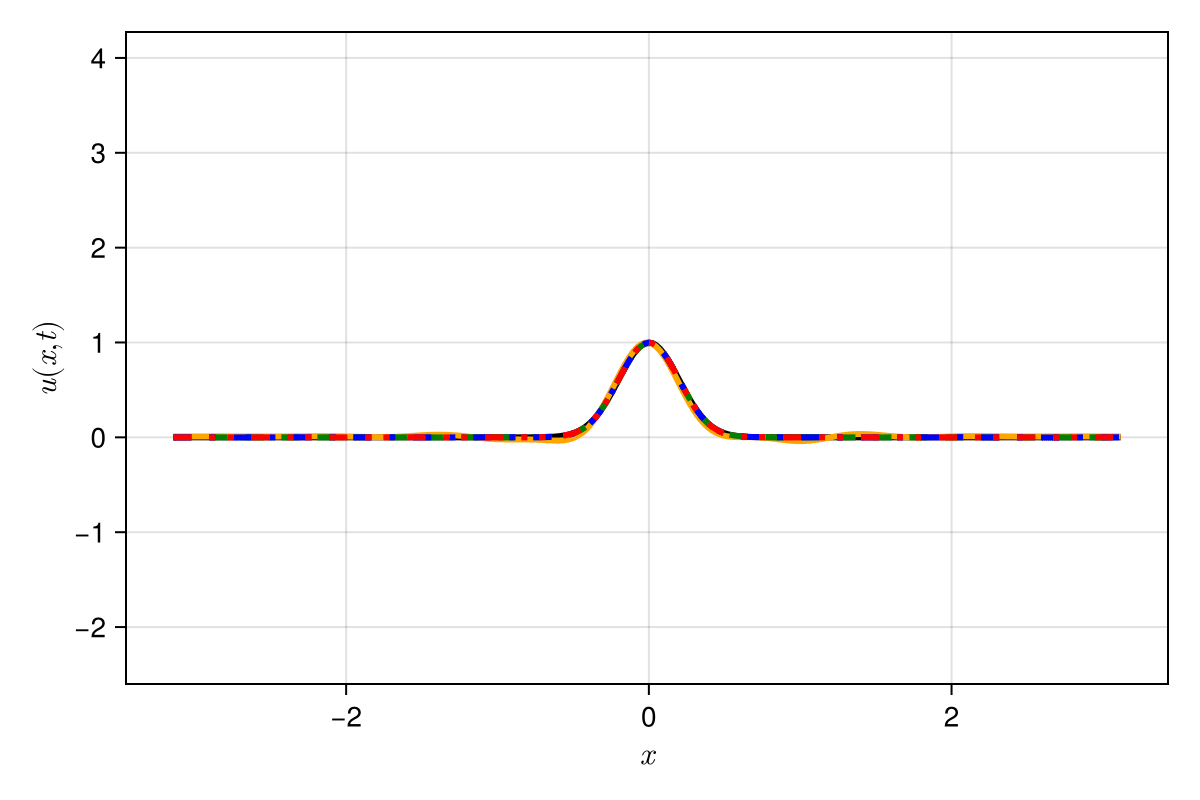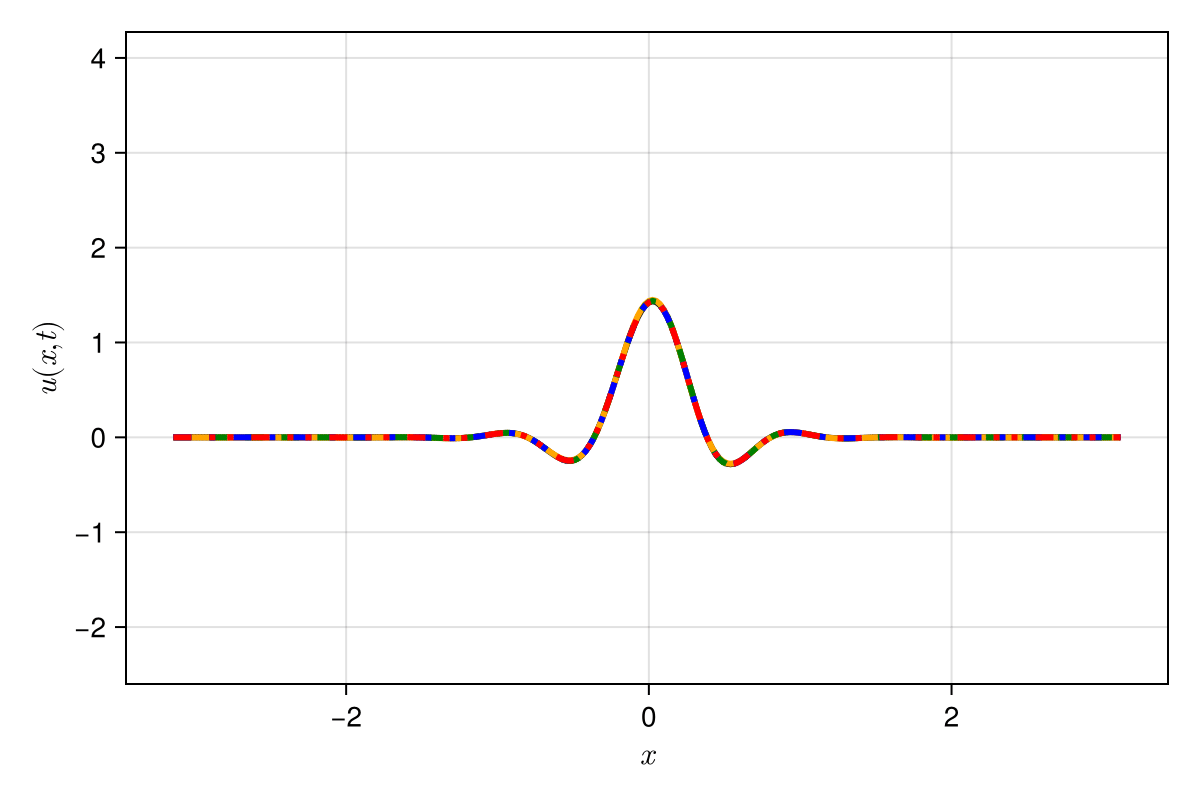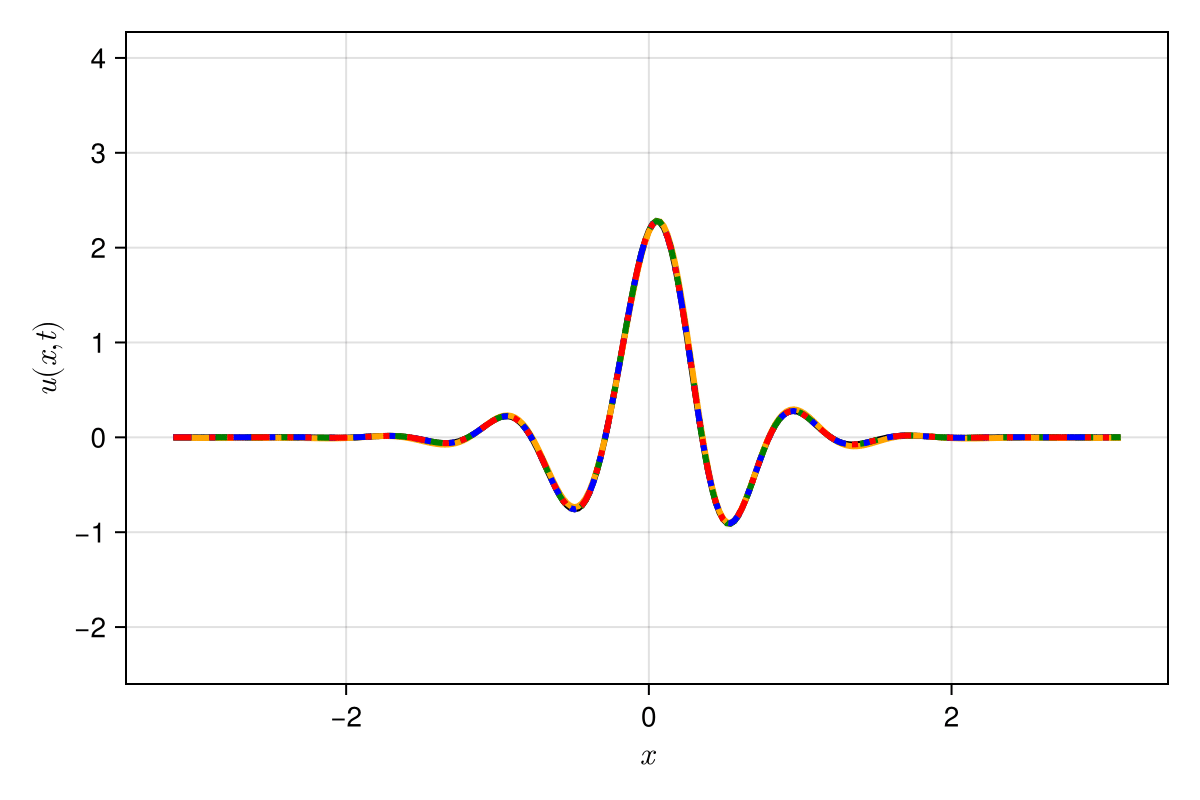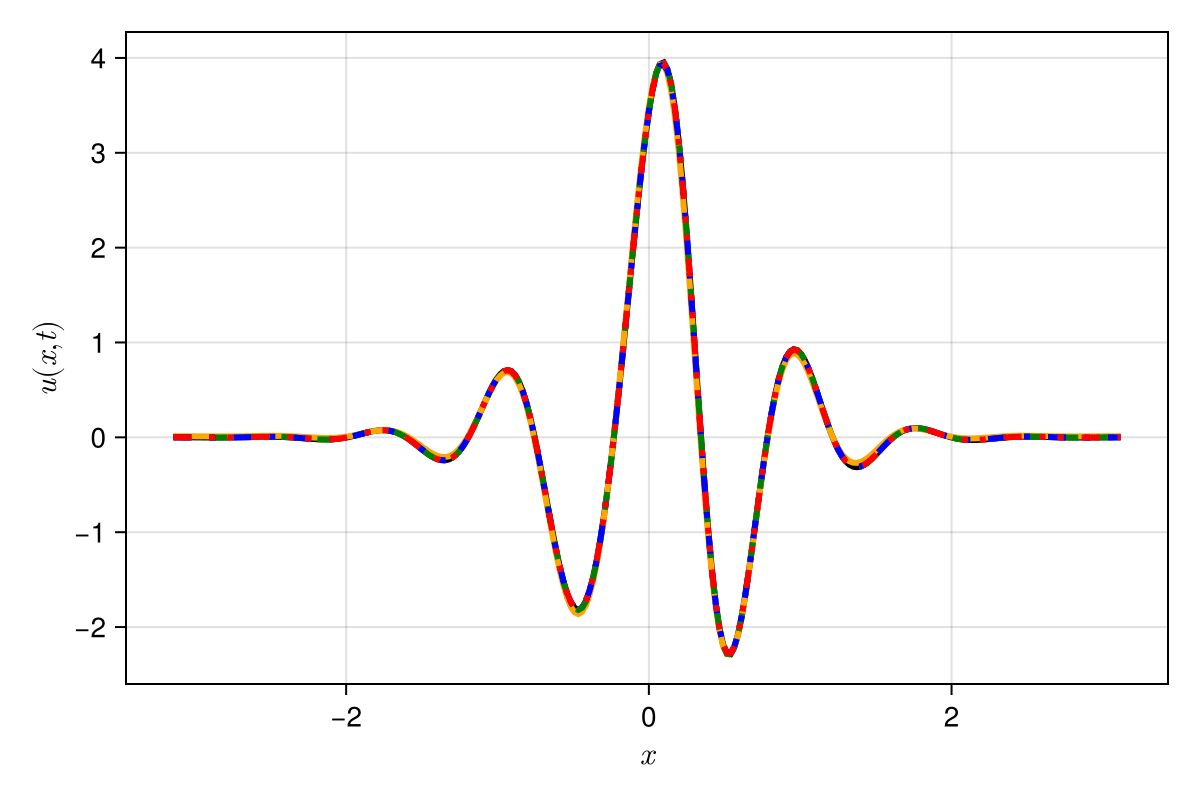
\frac{\partial {u}}{\partial t} + u\frac{\partial {u}}{\partial x} + \frac{\partial^2 {u}}{\partial x^2} + \nu\frac{\partial^4 {u}}{\partial x^4} = 0

\(\text{Predictions}\)

\(\text{Relative error } (\Delta t = \Delta t_0)\)

\(\text{Relative error } (\Delta t = 10\Delta t_0)\)

Major takeaways

10

AB

Thanks for your attention.

Questions?

Scan QR code to access project website

Experiment: 1D viscous Burgers problem \((\mathit{Re} = 10\text{k})\)

10

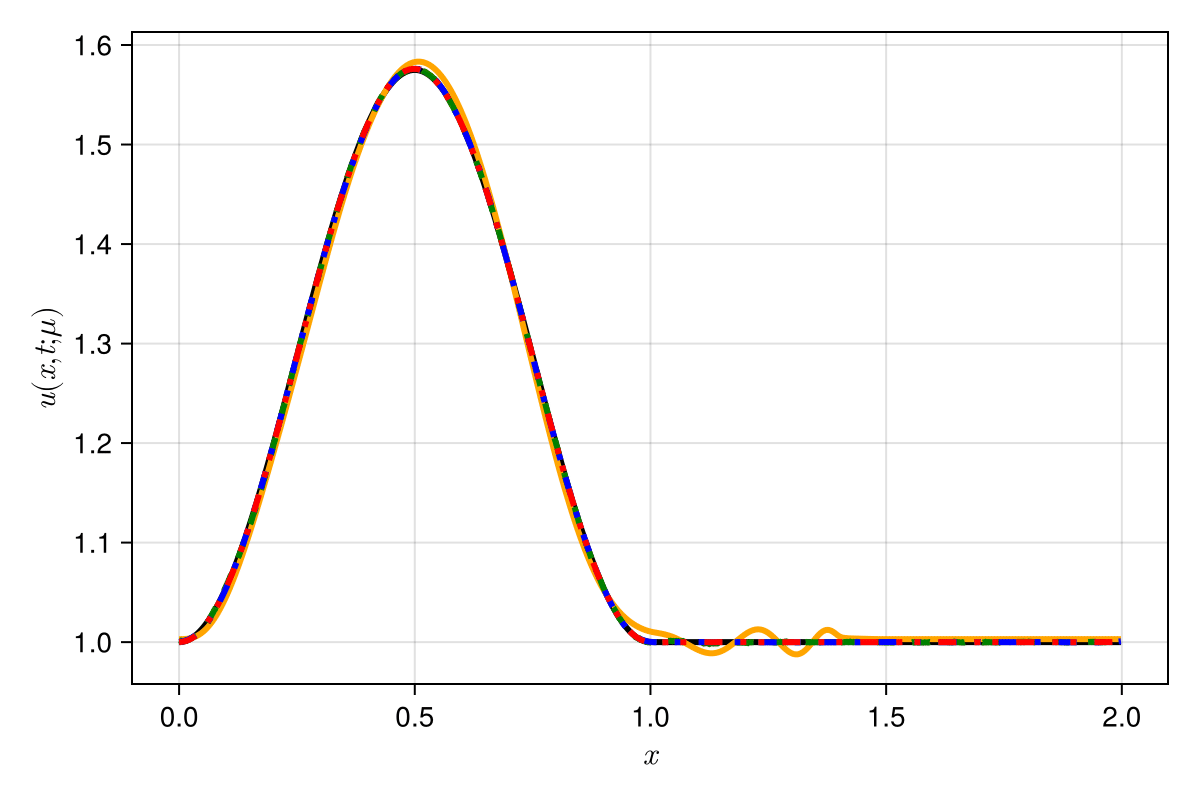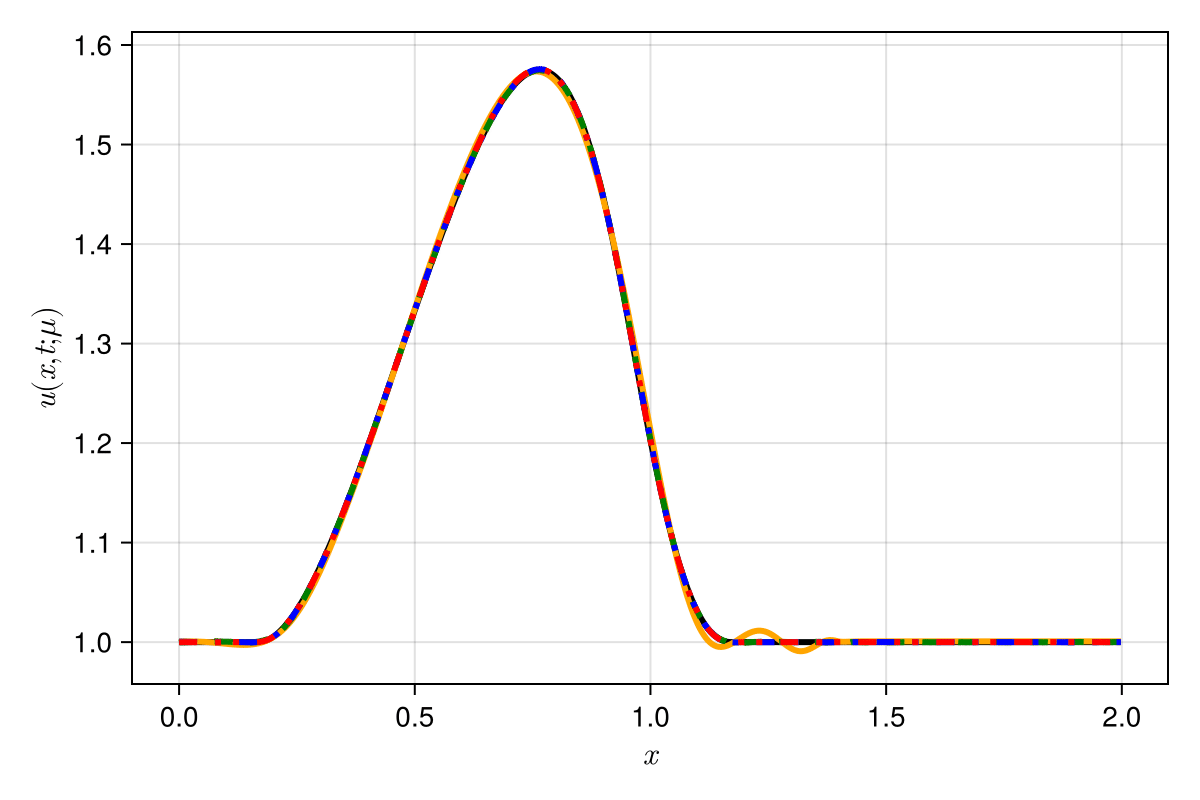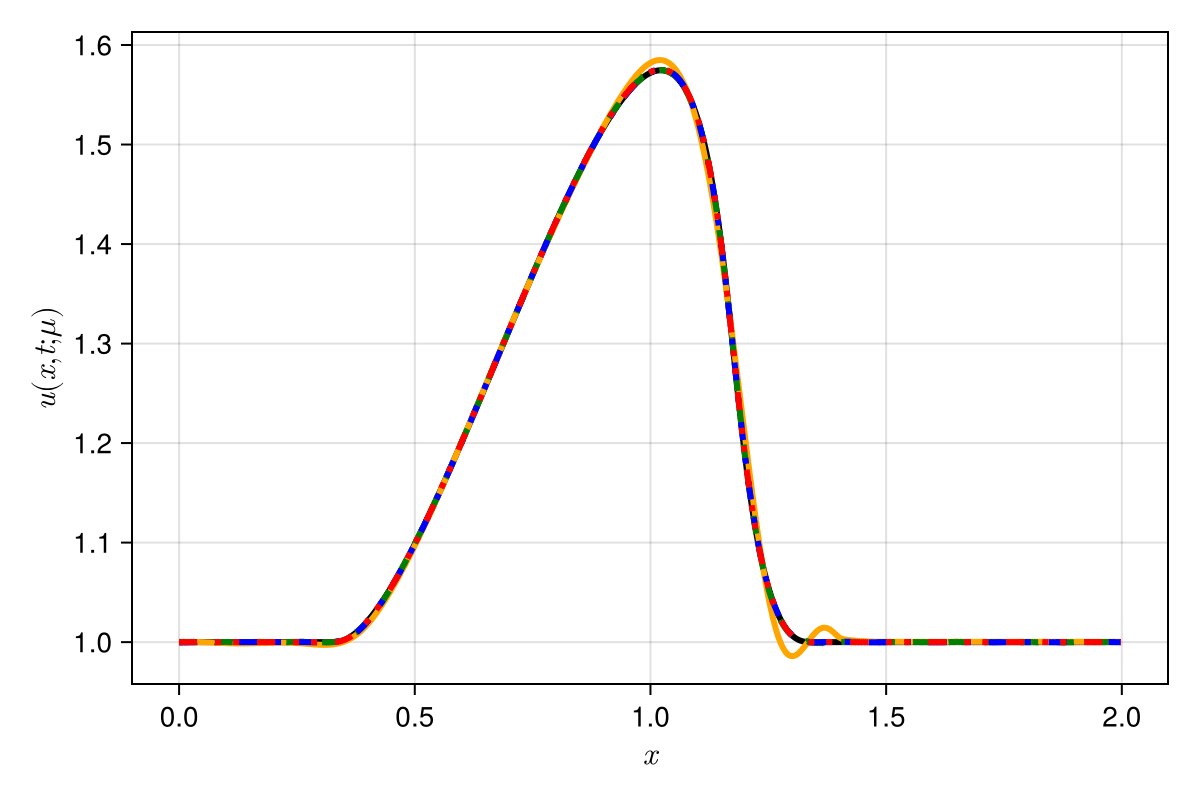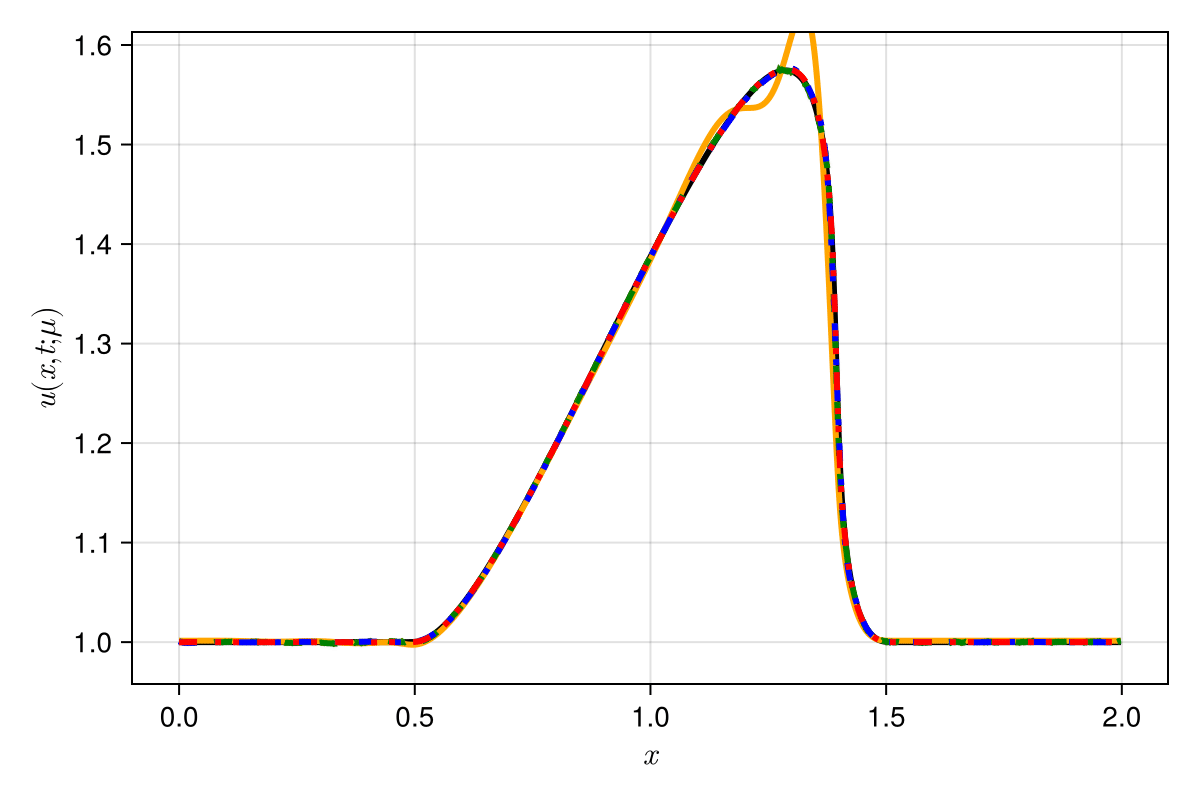
\(\text{Predictions}\)

\(\mu = 0.600 \text{ (training)}\)

\(\mu = 0.575 \text{ (inteprolation)}\)

\(\mu = 625 \text{ (extrapolation)}\)

\(\text{CAE-ROM}\)

\(\text{SNFL-ROM}\)

\(\text{SNFW-ROM}\)

Title

1

Model order reduction

1

\begin{pmatrix} \hspace{0.8em} \\ \\ \\ \\ \end{pmatrix}
\begin{pmatrix} \hspace{0.8em} \\ \\ \\ \\ \end{pmatrix}
\mathbb{R}^{N_\text{FOM}}
\bar{u}(0)
\bar{u}(T)
\text{Full-order model (FOM)}
\text{Linear ROM}
\text{Nonlinear ROM}
\text{POD Manifold}

Plan for presentation

  • Motivation
    • Accelerate PDE solvers. show 2D Burg as example
  • Model order reduction
    • make animation akin to poster. Compare e_proj vs N
  • CAEs: analyze increasing error in time-evolution
  • Fix: directly model the intrinsic ROM manifold (Sec. 4.1)
  • Show examples
  • INRs: non-differentiability. large errors in time-evolution
  • Fix: neural field regularization (Sec. 4.2)
  • Results: compare accuracy and speed-up
  • Conclusions

1

Notes

  • Motivating acceleration example
  • MOR: make anim for MOR akin to poster. di
  •