Online Learning via Prediction with Experts' Advice
Victor Sanches Portella

UBC - CS
June 2022
Experts' Problem and Online Learning
Prediction with Experts' Advice
Player
Adversary
\(n\) Experts
0.5
0.1
0.3
0.1
Probabilities
1
0
0.5
0.3
Costs
Player's loss:
Adversary knows the strategy of the player
Picking a random expert
vs
Picking a probability vector
Measuring Player's Perfomance
Total player's loss
Can be = \(T\) always
Compare with offline optimum
Almost the same as Attempt #1
Restrict the offline optimum
Attempt #1
Attempt #2
Attempt #3
Loss of Best Expert
Player's Loss
Goal:
Example
Cummulative Loss
Experts
General Online Learning
Player
Adversary
Player's loss:
Convex
The player sees \(f_t\)
Simplex
Linear functions
Some usual settings:
Experts' problem
Why Online Learning?
Traditional ML optimization makes stochastic assumptions on the data
OL strips away the stochastic layer
Traditional ML optimization makes stochastic assumptions on the data
Less assumptions \(\implies\) Weaker guarantees
Less assumptions \(\implies\) More robust
Adaptive algorithms
AdaGrad
Adam
Parameter Free algorithms
Coin Betting
Meta-optimization
Algorithms
Follow the Leader
Idea: Pick the best expert at each round
where \(i\) minimizes
Can fail badly
Player loses \(T -1\)
Best expert loses \(T/2\)
Works very well for quadratic losses
* picking distributions instead of best expert
Gradient Descent
\(\eta_t\): step-size at round \(t\)
\(\ell_t\): loss vector at round \(t\)
Sublinear Regret!
Optimal dependency on \(T\)
Can we improve the dependency on \(n\)?
Yes, and by a lot
Multiplicative Weights Update Method
Normalization
Exponential improvement on \(n\)
Optimal
Other methods had clearer "optimization views"
Rediscovered many times in different fields
This one has an optimization view as well!
Follow the Regularized Leader
Regularizer
"Stabilizes the algorithm"
"Lazy" Gradient Descent
Multiplicative Weights Update
Good choice of \(R\) depends of the functions and the feasible set
Online Mirror Descent
projection
Online Mirror Descent
Dual
Primal
Bregman
Projection
Regularizer
GD:
MWU:
OMD and FTRL are quite general

Applications
Approximately Solving Zero-Sum Games
Payoff matrix \(A\) of row player
Row player
Column player
Strategy \(p = (0.1~~0.9)\)
Strategy \(q = (0.3~~0.7)\)
Von Neumman min-max Theorem:
Row player
picks row \(i\) with probability \(p_i\)
Column player
picks column \(j\) with probability \(q_j\)
Row player
gets \(A_{ij}\)
Column player
gets \(-A_{ij}\)
Approximately Solving Zero-Sum Games
Main idea: make each row of \(A\) be an expert
For \(t = 1, \dotsc, T\)
\(p_1 =\) uniform distribution
Loss vector \(\ell_t\) is the \(j\)-th col. of \(-A\)
Get \(p_{t+1}\) via Multiplicative Weights
Thm:
Cor:
where \(j\) maximizes \(p_t^T A e_j\)
\(q_t = e_j\)
\(\bar{p} = \tfrac{1}{T} \sum_{t} p_t\)
\(\bar{q} = \tfrac{1}{T} \sum_{t} q_t\)
and
Boosting
Training set
Hypothesis class
of functions
Weak learner:
such that
Question: Can we get with high probability a hypothesis* \(h^*\) such that
only on a \(\varepsilon\)-fraction of \(S\)?
Generalization follows if \(\mathcal{H}\) is simple (and other conditions)
Boosting
For \(t = 1, \dotsc, T\)
\(p_1 =\) uniform distribution
\(\ell_t(i) = 1 - 2|h_t(x_i) - y_i|\)
Get \(p_{t+1}\) via Multiplicative Weights (with right step-size)
\(h_t = \mathrm{WL}(p_t, S)\)
\(\bar{h} = \mathrm{Majority}(h_1, \dotsc, h_T)\)
Theorem
If \(T \geq (2/\gamma^2) \ln(1/\varepsilon)\), then \(\bar{h}\) makes at most \(\varepsilon\) mistakes in \(S\)
Main ideas:
Regret only against distrb. on examples that \(\bar{h}\) errs
Due to WL property, loss of the player is \(\geq 2 T \gamma\)
\(\ln n\) becomes \(\ln (n/\mathrm{\# mistakes}) \)
Cost of any distribution of this type is \(\leq 0\)
From Electrical Flows to Maximum Flow

Goal:
Route as much flow as possible from \(s\) to \(t\) while respecting the edges' capacities
We can compute in time \(O(|V| \cdot |E|)\)
This year there was a paper with a \(O(|E|^{1 + o(1)})\) alg...
What if we want something faster even if approx.?
From Electrical Flows to Maximum Flow
Fast Laplacian system solvers (Spielman & Teng' 13)
We can compute electrical flows by solving this system
Electrical flows may not respect edge capacities!

Solves
in \(\tilde{O}(|E|)\) time
Laplacian matrix of \(G\)
Main idea: Use electrical flows as a "weak learner", and boost it using MWU!
Edges = Experts
Cost = flow/capacity
Other applications (beyond experts)
Solving Packing linear systems with oracle access
Approximating multicommodity flow
Approximately solve some semidefinite programs
Spectral graph sparsification
Approximating multicommodity flow
Computational complexity (QIP = PSPACE)
Anytime Regret and Stochastic Calculus
Fixed-time vs Anytime
MWU regret
when \(T\) is known
when \(T\) is not known
anytime
fixed-time
Does knowing \(T\) gives the player an advantage?
Mirror descent in anytime can fail terribly
[Huang, Harvey, VSP, Friedlander]
Optimum for 2 experts anytime is worse
[Harvey, Liaw, Perkins, Randhawa]
Similar techniques also work for fixed-time
[Greenstreet, Harvey, VSP]
Continuous-time experts show interesting behaviour
[VSP, Liaw, Harvey]
Random Experts' Costs
What happens when we randomize experts' losses?
Culmulative loss
of expert \(i\) is a random walk
independently
Worst-case adversary:
Regret bound hold with probability 1
Regret bound against any adversary
Idea: Move to continuous time to use powerful stochastic calculus tools
Worked very well with 2 experts
Moving to Continuous Time
Moving to continuous time:

Random walk \(\longrightarrow\) Brownian Motion

are Independent Brownian motions
where
Moving to Continuous Time
Discrete time
Continuous time
Cummulative loss
Player's cummulative loss
Player's loss per round
MWU in Continuous Time
Potential based players
Regret bounds
when \(T\) is known
when \(T\) is not known
anytime
fixed-time
MWU!
Same as discrete time!
Idea: Use stochastic calculus to guide the algorithm design
with prob. 1
New Algorithms in Continuous Time
Potential based players
Matches fixed-time!
Stochastic calculus suggests pontential that satisfy the Backwards Heat Equation
This new algorithm has good regret!
Does not translate easily to discrete time
need to add correlation between experts
New algorithms with good quantile regret bounds!
Fixed-time vs Anytime is still open!
Online Learning via Prediction with Experts' Advice
Victor Sanches Portella

UBC - CS
June 2022
Kitchen Sink
Simplifying Assumptions
We will look only at \(\{0,1\}\) costs
1
0
0
1
0
0
1
1
Equal costs do not affect the regret
Cover's algorithm relies on these assumptions by construction
Our alg. and analysis extends to fractional costs
Gap between experts
Thought experiment: how much probability mass to put on each expert?
Cumulative Loss on round \(t\)
\(\frac{1}{2}\) is both cases seems reasonable!
Takeaway: player's decision may depend only on the gap between experts's losses
Gap = |42 - 20| = 22
Worst Expert
Best Expert
42
20
2
2
42
42
(and maybe on \(t\))
Cover's Dynamic Program
Player strategy based on gaps:
Choice doesn't depend on the specific past costs
on the Worst expert
on the Best expert
We can compute \(V^*\) backwards in time via DP!
Max regret to be suffered at time \(t\) with gap \(g\)
\(O(T^2)\) time to compute \(V^*\)
At round \(t\) with gap \(g\)
Max. regret for a game with \(T\) rounds
Computing the optimal strategy \(p^*\) from \(V^*\) is easy!
Cover's DP Table
(w/ player playing optimally)
Cover's Dynamic Program
Player strategy based on gaps:
Choice doesn't depend on the specific past costs
on the Lagging expert
on the Leading expert
We can compute \(V^*\) backwards in time via DP!
Getting an optimal player \(p^*\) from \(V^*\) is easy!
Max regret-to-be-suffered at round \(t\) with gap \(g\)
\(O(T^2)\) time to compute the table — \(O(T)\) amortized time per round
At round \(t\) with gap \(g\)
Optimal regret for 2 experts
Connection to Random Walks
Optimal player \(p^*\) is related to Random Walks
For \(g_t\) following a Random Walk
Central Limit Theorem
Not clear if the approximation error affects the regret
The DP is defined only for integer costs!
Lagging expert finishes leading
Let's design an algorithm that is efficient and works for all costs
Bonus: Connections of Cover's algorithm with stochastic calculus
Connection to Random Walks
Theorem
Player \(p^*\) is also connected to RWs
For \(g_t\) following a Random Walk
Central Limit Theorem
Not clear if the approximation error affects the regret
The DP is defined only for integer costs!
Lagging expert finishes leading
[Cover '67]
# of 0s of a Random Walk of len \(T\)
Let's design an algorithm that is efficient and works for all costs
Bonus: Connections of Cover's algorithm with stochastic calculus
Discrete Itô's Formula
How to analyze a discrete algorithm coming from stochastic calculus?
Discrete Itô's Formula!
Discrete Derivatives
Surprisingly, we can analyze Cover's algorithm with discrete Itô's formula
Itô's Formula
Discrete Itô's Formula
Discrete Algorithms
\(V^*\) satisfies the "discrete" Backwards Heat Equation!
Not Efficient
Efficient
Discrete Itô \(\implies\)
Regret of \(p^* \leq V^*[0,0]\)
BHE = Optimal?
Hopefully, \(R\) satisfies the discrete BHE
Discretized player:
We show the total is \(\leq 1\)
Cover's strategy
Bounding the Discretization Error
In the work of Harvey et al., they had
In this fixed-time solution, we are not as lucky.
Negative discretization error!
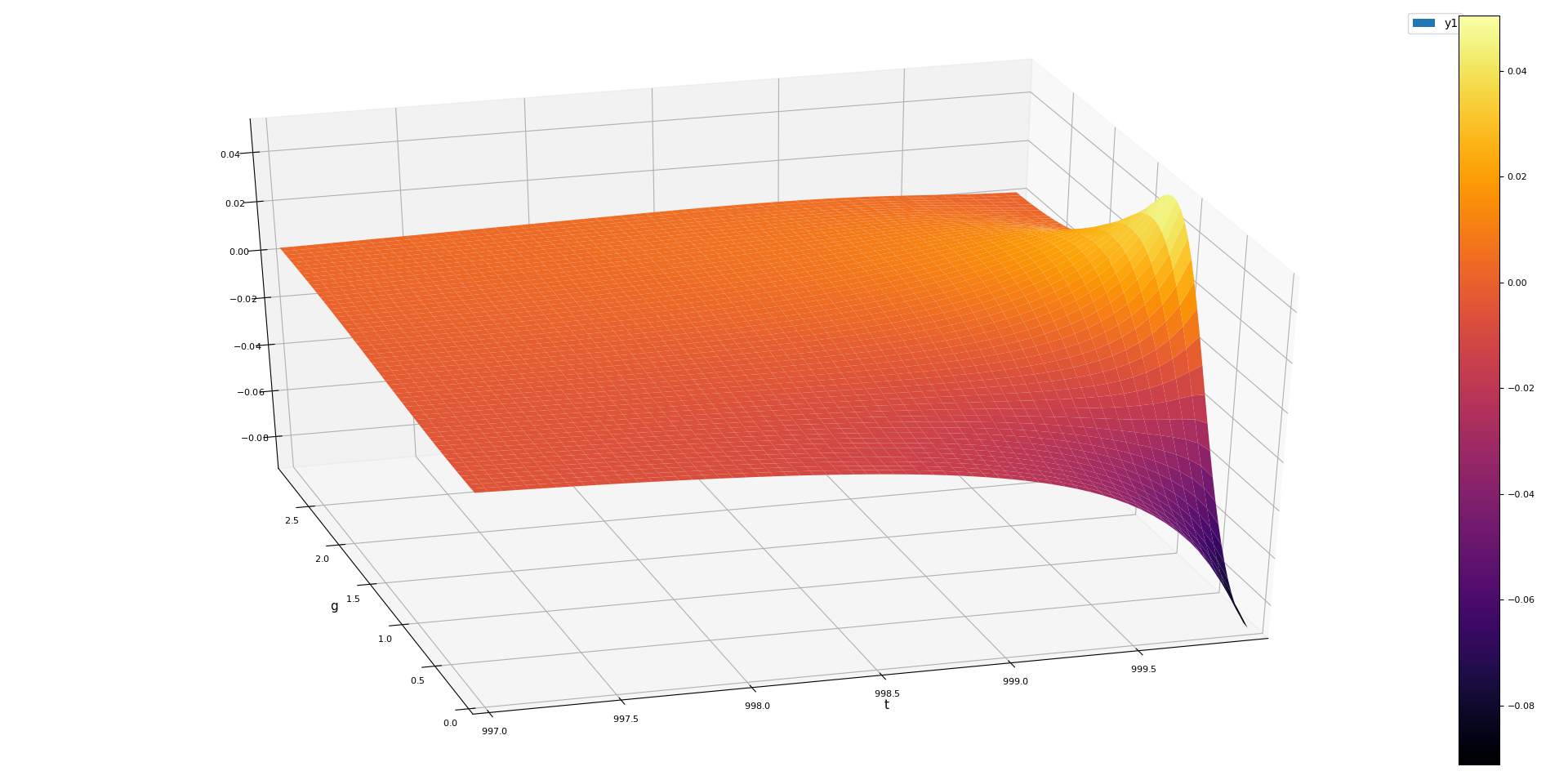
We show the total discretization error is always \(\leq 1\)
A Probabilistic View of Regret Bounds
Formula for the regret based on the gaps
Random walk \(\longrightarrow\) Brownian Motion
Reflected Brownian motion (gaps)
Conditions on the continuous player \(p\)
Continuous on \([0,T) \times \mathbb{R}\)
for all \(t \geq 0\)
Stochastic Integrals and Itô's Formula
How to work with stochastic integrals?
Itô's Formula:
\(\overset{*}{\Delta} R(t, g) = 0\) everywhere
ContRegret \( = R(T, |B_T|) - R(0,0)\)
Goal:
Find a "potential function" \(R\) such that
(1) \(\partial_g R\) is a valid continuous player
(2) \(R\) satisfies the Backwards Heat Equation
Different from classic FTC!
Backwards Heat Equation
Stochastic Integrals and Itô's Formula
Goal:
Find a "potential function" \(R\) such that
(1) \(\partial_g R\) is a valid continuous player
(2) \(R\) satisfies the Backwards Heat Equation
How to find a good \(R\)?
?
Suffices to find a player \(p\) satisfying the BHE
\(\approx\) Cover's solution!
Also a solution to an ODE
Then setting
preserves BHE and
Stochastic Integrals and Itô's Formula
How to work with stochastic integrals?
Itô's Formula:
\(\overset{*}{\Delta} R(t, g) = 0\) everywhere
ContRegret is given by \(R(T, |B_T|)\)
Goal:
Find a "potential function" \(R\) such that
(1) \(\partial_g R\) is a valid continuous player
(2) \(R\) satisfies the Backwards Heat Equation
Different from classic FTC!
Backwards Heat Equation
[C-BL 06]
Our Results
An Efficient and Optimal Algorithm in Fixed-Time with Two Experts
Technique:
Solve an analogous continuous-time problem, and discretize it
[HLPR '20]
How to exploit the knowledge of \(T\)?
Discretization error needs to be analyzed carefully.
BHE seems to play a role in other problems in OL as well!
Solution based on Cover's alg
Or inverting time in an ODE!
We show \(\leq 1\)
\(V^*\) and \(p^*\) satisfy the discrete BHE!
Insight:
Cover's algorithm has connections to stochastic calculus!
Questions?
Known Results
Multiplicative Weights Update method:
Optimal for \(n,T \to \infty\) !
If \(n\) is fixed, we can do better
\(n = 2\)
\(n = 3\)
\(n = 4\)
Player knows \(T\) !
Minmax regret in some cases:
What if \(T\) is not known?
Minmax regret
\(n = 2\)
[Harvey, Liaw, Perkins, Randhawa FOCS 2020]
They give an efficient algorithm!
A Dynamic Programming View
Optimal regret (\(V^* = V_{p^*}\))
For \(g > 0\)
For \(g = 0\)
Regret and Player in terms of the Gap
Path-independent player:
If
round \(t\) and gap \(g_{t-1}\) on round \(t-1\)
on the Lagging expert
on the Leading expert
Choice doesn't depend on the specific past costs
for all \(t\), then
gap on round \(t\)
A discrete analogue of a Riemann-Stieltjes integral
A formula for the regret
A Dynamic Programming View
Maximum regret-to-be-suffered on rounds \(t+1, \dotsc, T\) when gap on round \(t\) is \(g\)
Path-independent player \(\implies\) \(V_p[t,g]\) depends only on \(\ell_{t+1}, \dotsc, \ell_T\) and \(g_t, \dotsc, g_{T}\)
Regret suffered on round \(t+1\)
Regret suffered on round \(t + 1\)
A Dynamic Programming View
Maximum regret-to-be-suffered on rounds \(t+1, \dotsc, T\) if gap at round \(t\) is \(g\)
We can compute \(V_p\) backwards in time!
Path-independent player \(\implies\)
\(V_p[t,g]\) depends only on \(\ell_{t+1}, \dotsc, \ell_T\) and \(g_t, \dotsc, g_{T}\)
We then choose \(p^*\) that minimizes \(V^*[0,0] = V_{p^*}[0,0]\)
Maximum regret of \(p\)
A Dynamic Programming View
For \(g > 0\)
Optimal player
Optimal regret (\(V^* = V_{p^*}\))
For \(g = 0\)
For \(g > 0\)
For \(g = 0\)
Discrete Derivatives
Bounding the Discretization Error
Main idea
\(R\) satisfies the continuous BHE
Approximation error of the derivatives
Lemma
Known and New Results
Multiplicative Weights Update method:
Optimal for \(n,T \to \infty\) !
If \(n\) is fixed, we can do better
Worst-case regret for 2 experts
Player knows \(T\) (fixed-time)
Player doesn't know \(T\) (anytime)
Question:
Is there an efficient algorithm for the fixed-time case?
Ideally an algorithm that works for general costs!
\(O(T)\) time per round
Dynamic Programming
\(\{0,1\}\) costs
\(O(1)\) time per round
Stochastic Calculus
\([0,1]\) costs
[Harvey, Liaw, Perkins, Randhawa FOCS 2020]
[Cover '67]
Our Results
Result:
An Efficient and Optimal Algorithm in Fixed-Time with Two Experts
\(O(1)\) time per round
was \(O(T)\) before
Holds for general costs!
Technique:
Discretize a solution to a stochastic calculus problem
[HLPR '20]
How to exploit the knowledge of \(T\)?
Non-zero discretization error!
Insight:
Cover's algorithm has connections to stochastic calculus!
This connection seems to extend to more experts and other problems in online learning in general!