Riga Technical University


WHERE is the TELE-TRAFFIC here?


PROBLEM Nr1



WHERE is the TELE-TRAFFIC here?




PROBLEM Nr2
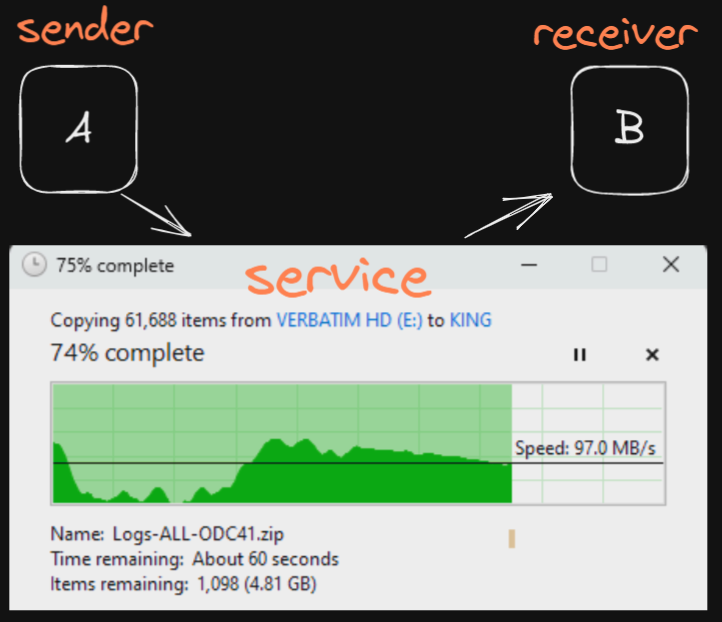
Digital Communication Flow in
Parcel Service
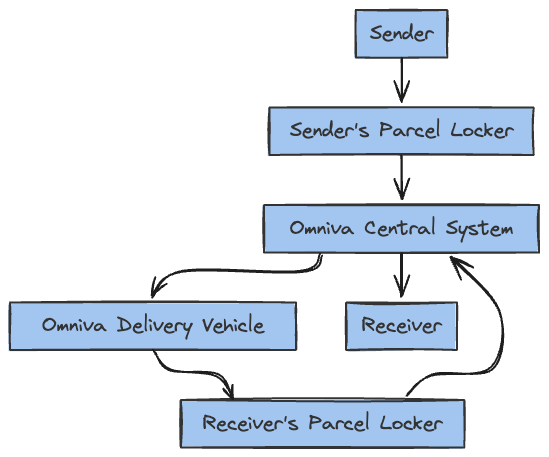
WHERE is the TELE-TRAFFIC here?

PROBLEM Nr3
Course (RAE-555) Life-Span

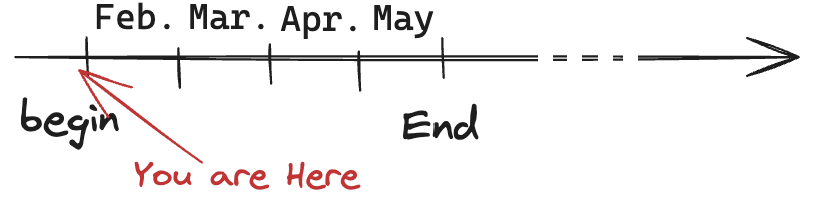
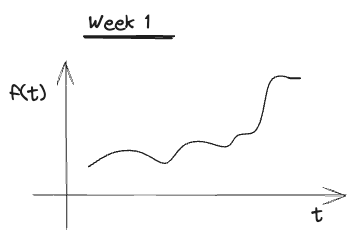
Week 1
2024.01.29
Course (RAE-555) Life-Span


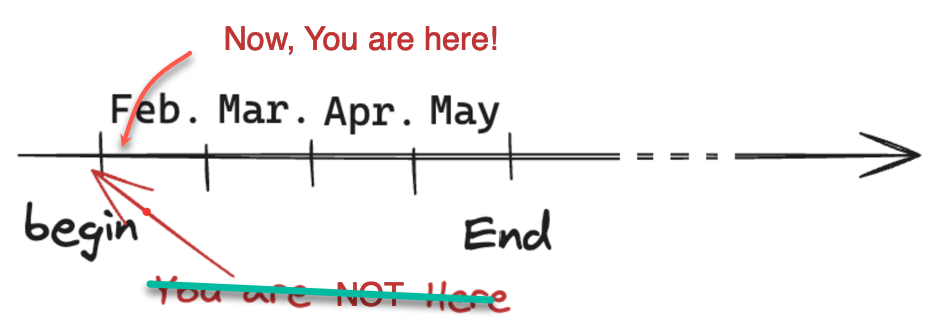
Week 1
Week 2
2024.01.29
2024.02.05

WHERE is the TELE-TRAFFIC in this MODEL?

PROBLEM Nr4
WHAT is the TRAFFIC?
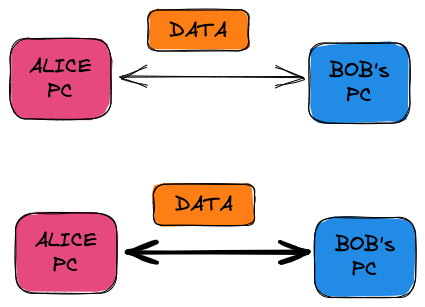
a)
b)


PROBLEM Nr5

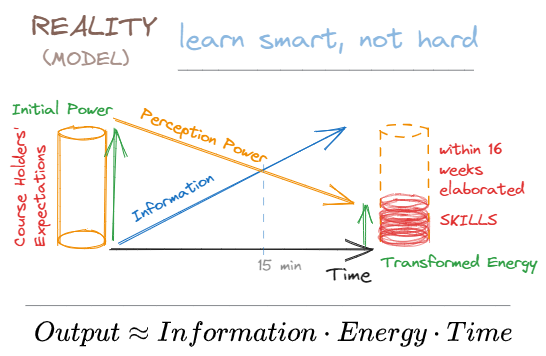
HOW
TELE-TRAFFIC THEORY
is HELPFUL for US ?






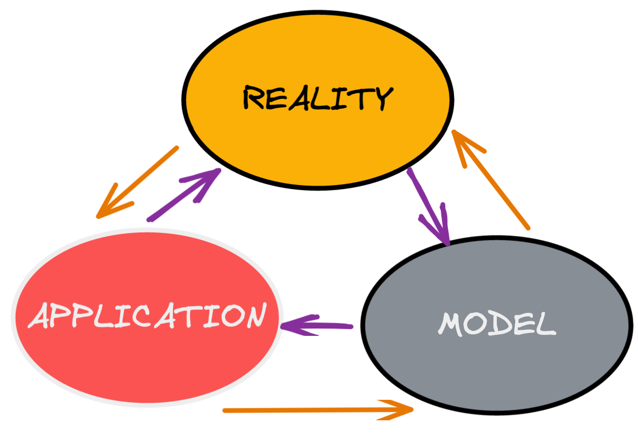
THEORY

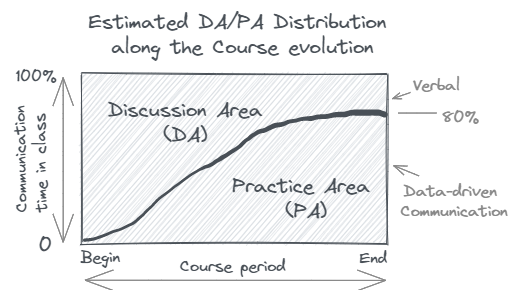
BUSINESS-ORIENTED LEARNING MODEL
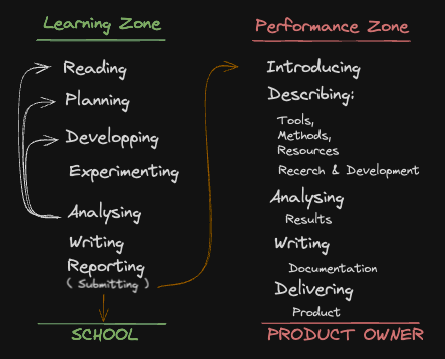

BUSINESS-ORIENTED LEARNING MODEL

2024.01.29
2024.05.31
WHAT is the TRAFFIC?

a)
b)


What are the TRAFFIC METRICS?
WHERE is the TRAFFIC?
a)
b)


PROBLEM Nr6
What are the TRAFFIC METRICS?
WHERE is the TRAFFIC?
a)
b)


PROBLEM Nr7
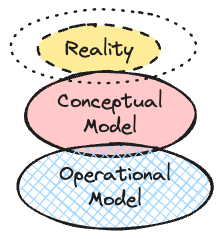
OPERATIONAL
MODEL instantiated as APPLICATION


METRICS & UNITS
OPERATIONAL
MODEL instantiated as APPLICATION


METRICS & UNITS
It's TIME to EXERCISE
PROBLEM Nr8
WEEK 1
Observe & Think
Develop &
Deploy
Run & Relax





Week # 2
Observing
Systems

METRICS
& UNITS
Considering Traffic as a
Service System Load

Dynamic Model
Static Model


What is the queue size?
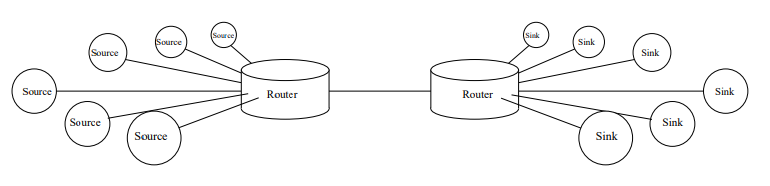
REAL NETWORK MODEL
Considering Traffic as a
Service System Load
What is the router load?
How long will stay the yellow packet in the queue?
How long will be processed the green packet?


TRAFFIC as a
Service System Load
(Jobs, Tasks, Customers, Cars, Data packets, Bytes, etc. )

Math Model
Conceptual Model



Course Book

https://www.amazon.com/Fundamentals-Queueing-Theory-Probability-Statistics/dp/111894352X/ref=sr_1_6?s=books&ie=UTF8&qid=1510840499&sr=1-6&keywords=fundamentals+of+queueing






Single Node Model
Fundamental Models


Little's Formula
Fundamental Models



Erlang's A Formula
Fundamental Models



Arrival Rate
Fundamental Models



Departure Rate
Fundamental Models



Waiting Time vs Departure Rate
Fundamental Models



Little formula and Erlang formula
Fundamental Models



From
OBSERVATION
to
MODEL DATA
Fundamental Models


ARRIVAL RATE
Fundamental Models


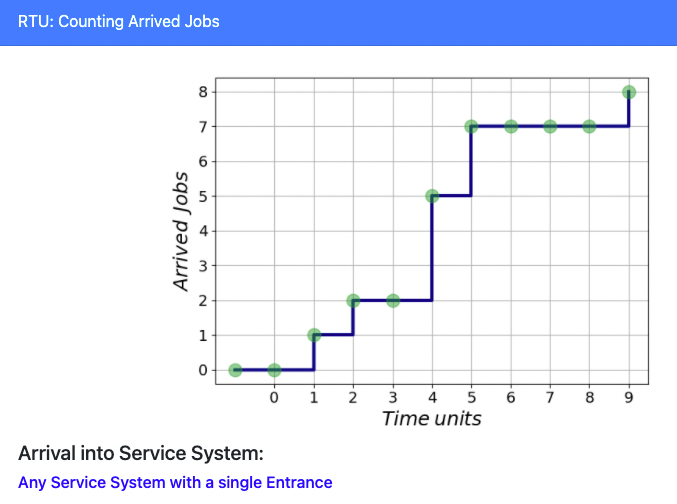
WHERE is the ARRIVAL here?


PROBLEM Nr 2.1
ARRIVAL RATE
Fundamental Models


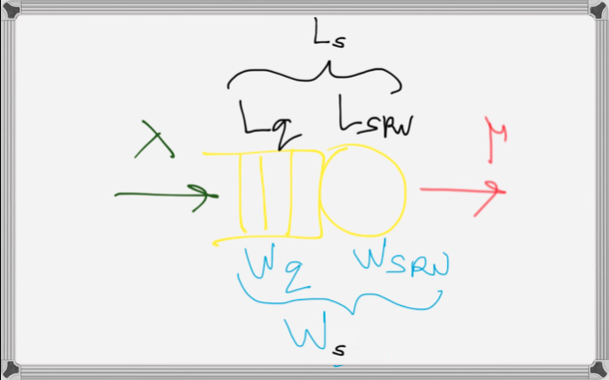
Problem Domain
Fundamental Models
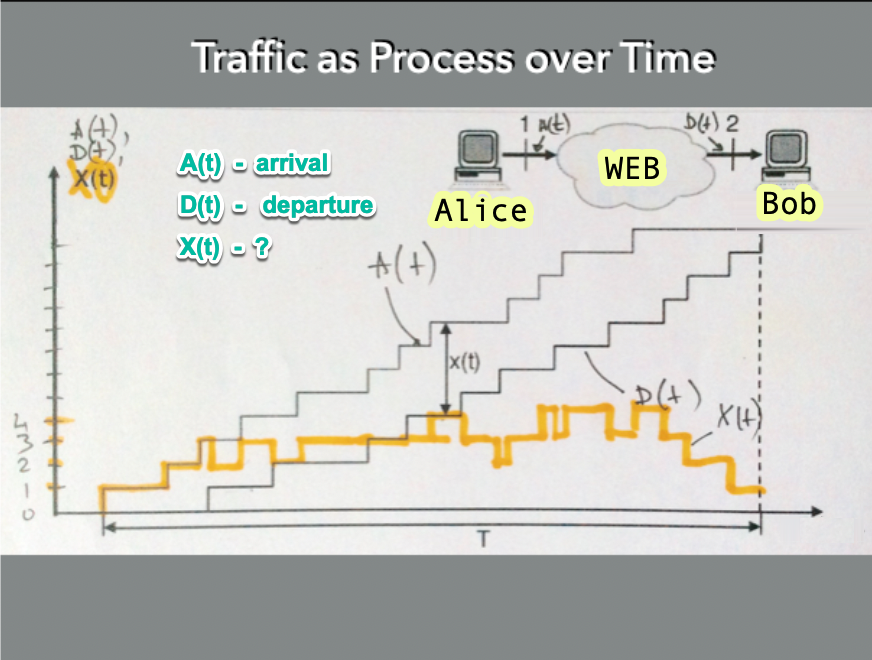


TRAFFIC as a PROCESS over TIME

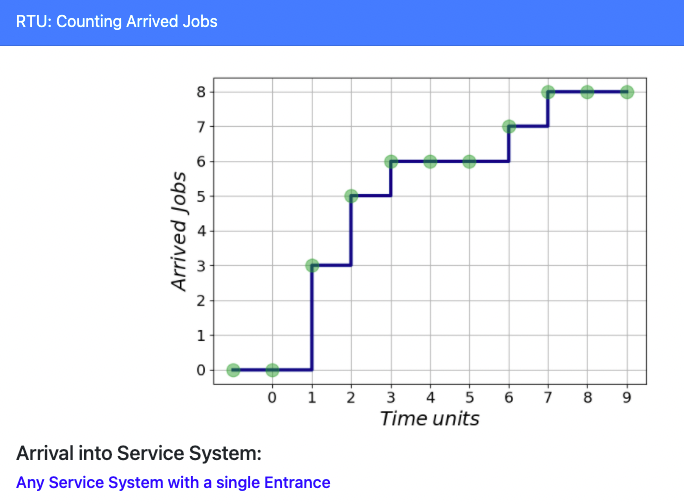

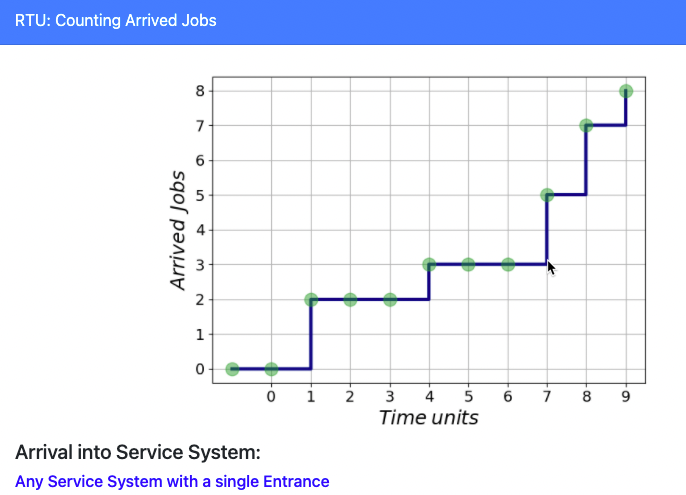



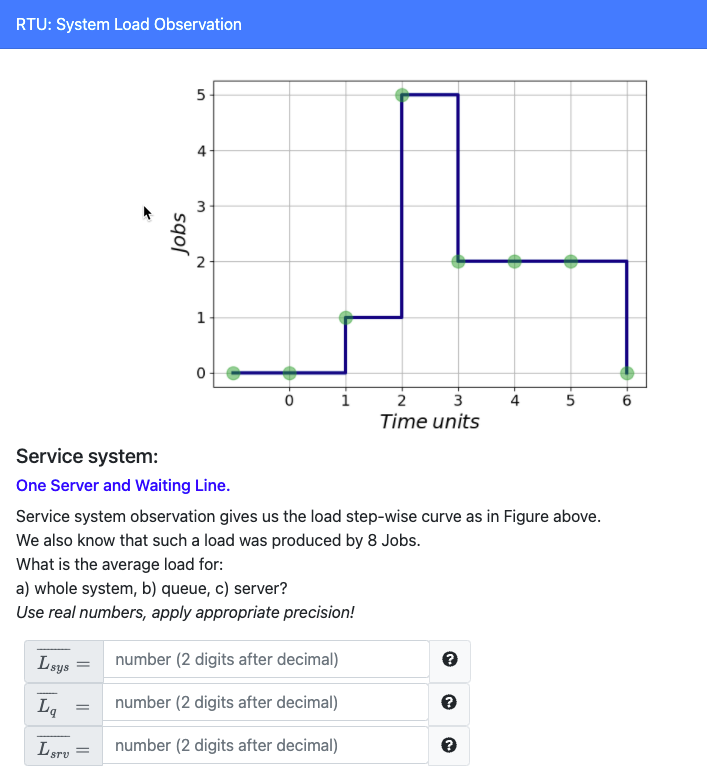

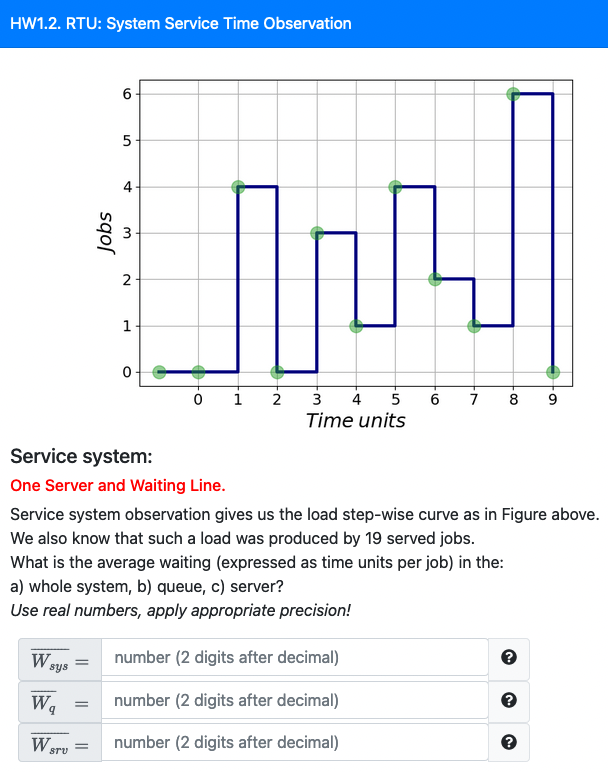

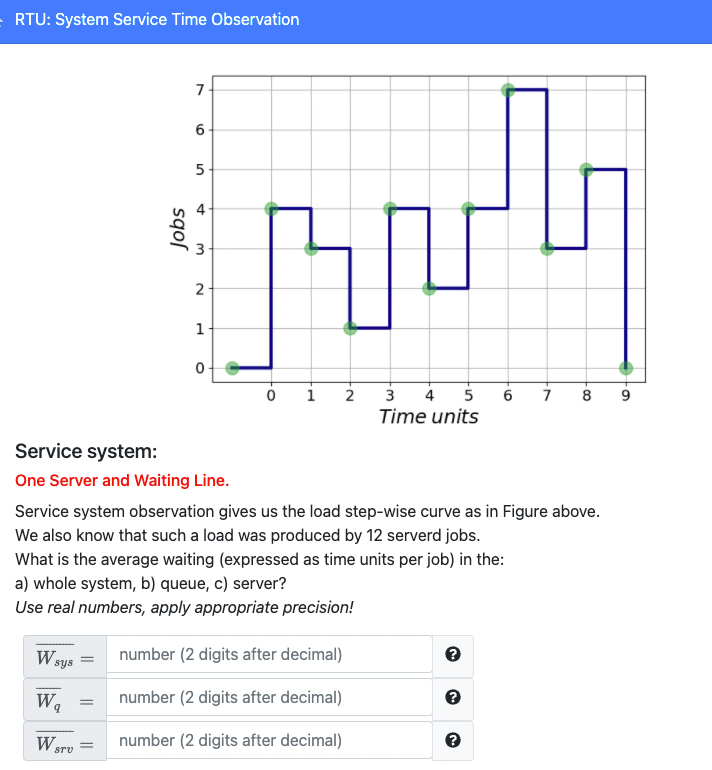

Questions
Fundamental Models


Course Book

https://www.amazon.com/Fundamentals-Queueing-Theory-Probability-Statistics/dp/111894352X/ref=sr_1_6?s=books&ie=UTF8&qid=1510840499&sr=1-6&keywords=fundamentals+of+queueing



Fundamental Models



TRAFFIC as a PROCESS over TIME
PROBLEM Nr9
RTU RAE555
Teletraffic Theory (Spring 2024)
Pre-Class for Week 3
- Choose any service-related Single Node System
- Observe the system for some time
- Analyse the system identifying primary traffic (load-related) characteristics
- Demonstrate results and understanding of the topic:
- Use slides on SLIDES.COM
- Make a Screencast on YouTube or Vimeo (make a short video about the topic)
- Publish the outcome on the course SLACK channel before the next meetup
The output is based on unique and individual experience
Output ( TODO )
Homework
Analysis of a Single Node Service system
(paying attention to the following characteristics)

Just be Active!
Q&A
2024.02.05
Week #3
From Observation to Models

Fundamental Models


Client
Server


Fundamental Models
Client
Server

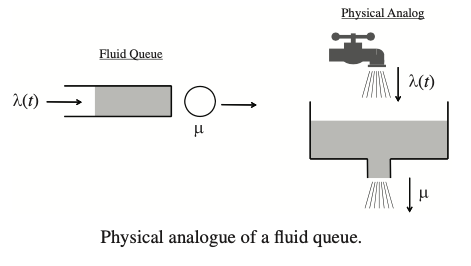
Fundamental Models


Fundamental Models
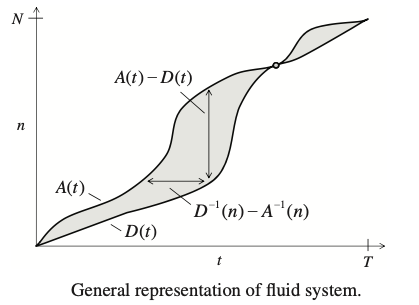

Fundamental Models
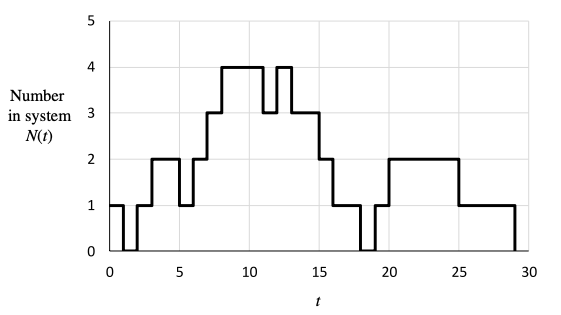

PROBLEM Nr10
Fundamental Models
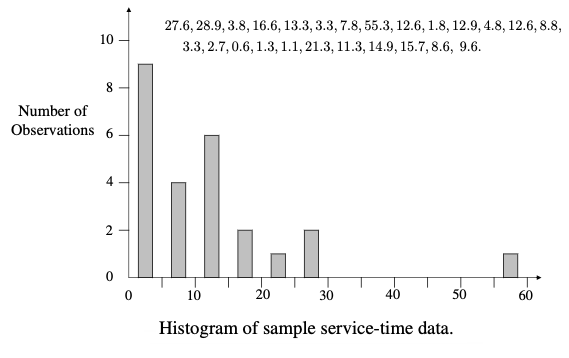

PROBLEM Nr11
Fundamental Models


Fundamental Models

In-Class problem

PROBLEM Nr12
RTU RAE555
Teletraffic Theory (Spring 2024)
In-Class for Week 4
- Analyse the given system identifying primary traffic characteristics
- Demonstrate results and the understanding of the topic:
- Use slides on SLIDES.COM and/or do handwriting + drawing
- Publish the outcome on the course SLACK channel Week-7 before the current Day (2024-xx-xx) ends
- Late submissions are allowed but not welcome.
The output is based on the given problem
Output ( TODO )
Homework
Analysis of a Single Node Service system
(paying attention to the following characteristics)

Week #4
From Observation to Models
2024-02-19

1st Module Exam
POSTPONED
RTU RAE555
Teletraffic Theory (Spring 2024)
Homework for Week 5
- Solve all the given problems related to HW1
- Demonstrate results and understanding of the topic
- Become ready for te Q1
The output is based on unique and individual variants
Output
Homework
Analysis of a Single Node Service system

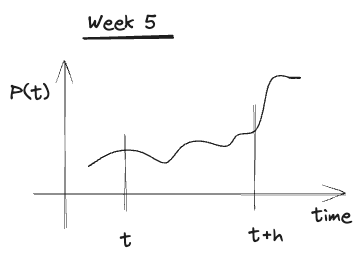
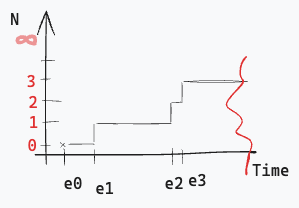
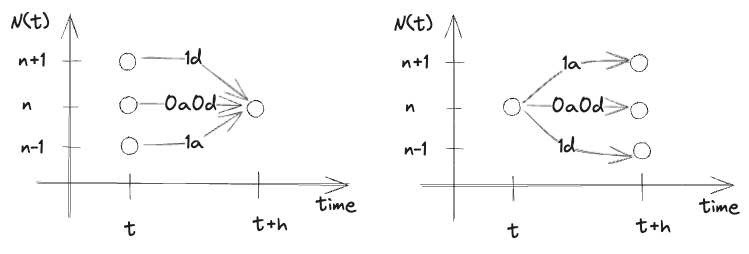
Week #5
From Observation to Models
2024-02-26

Week 5
Moving towards Reality


Books








Classwork Time

Week 5
Classwork
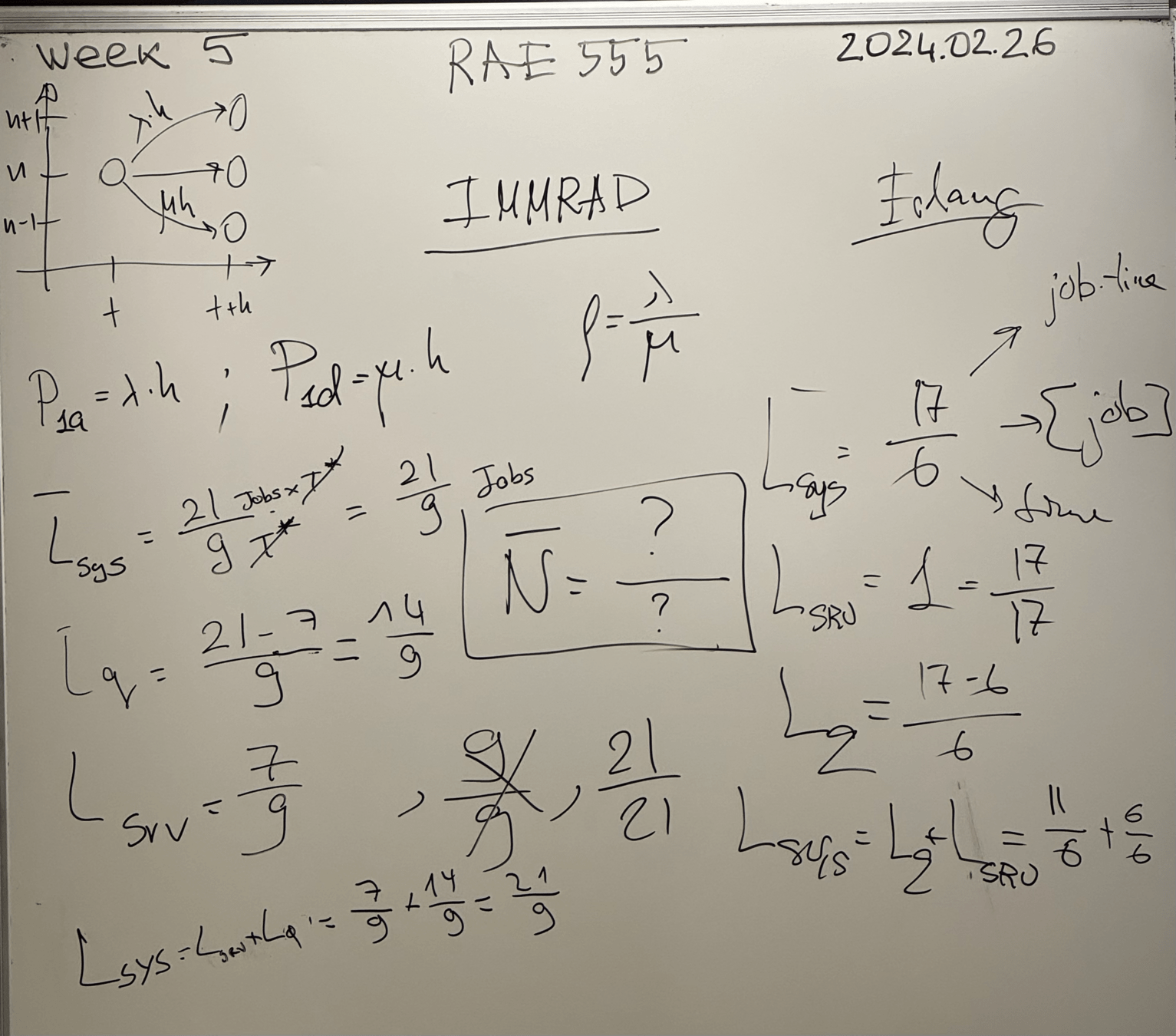
Week 5
Classwork
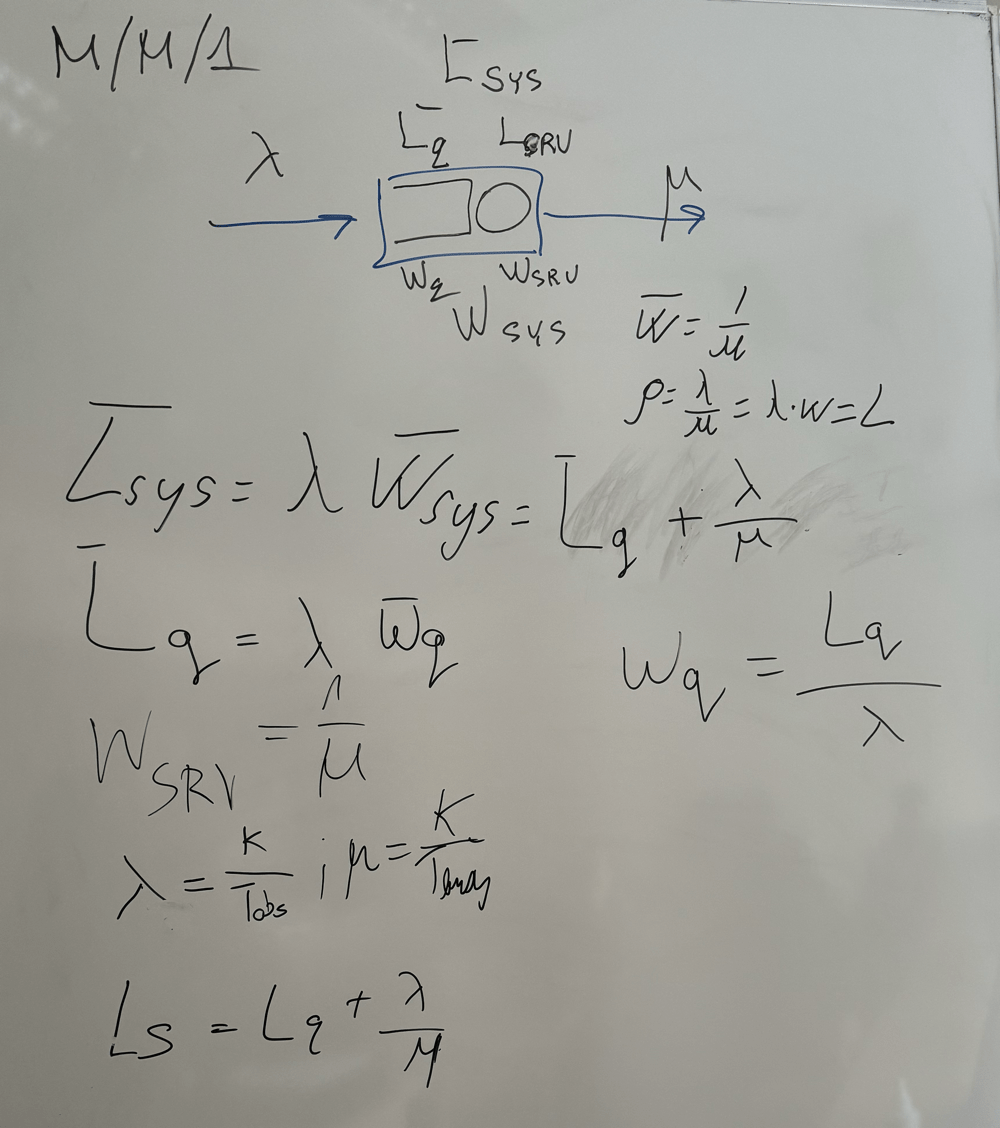
Moving towards Reality

RTU RAE555
Teletraffic Theory (Spring 2024)
Activities for Week 5 (HOMEWORK for Week 6)
- Participate in MADRAS UNI lectures Lec-30 and Lec-31
- Demonstrate understanding of the topic, and namely,
- Publish a recap of both lectures
The output can be complemented by unique and individual variants
Output
Homework
Theoretical Model of a Single Node Service system
TO DO that, proceed to

Week #6
From Observation to Models
2024-03-04

Week 6
Moving towards Reality


Week 6
FINITE SYSTEMS
Building Conceptual Understanding of
DTMC
(Discrete-Time Markov Chains)
Markov Chains

Week 6
FINITE SYSTEMS
DTMC
Markov Chains
CTMC

Books

Challenges
Markov Models


Books
https://www.wiley-vch.de/de/fachgebiete/mathematik-und-statistik/mathematik-16ma/diskrete-mathematik-16ma9/markov-chains-978-1-119-38755-8


Week 6
Homework
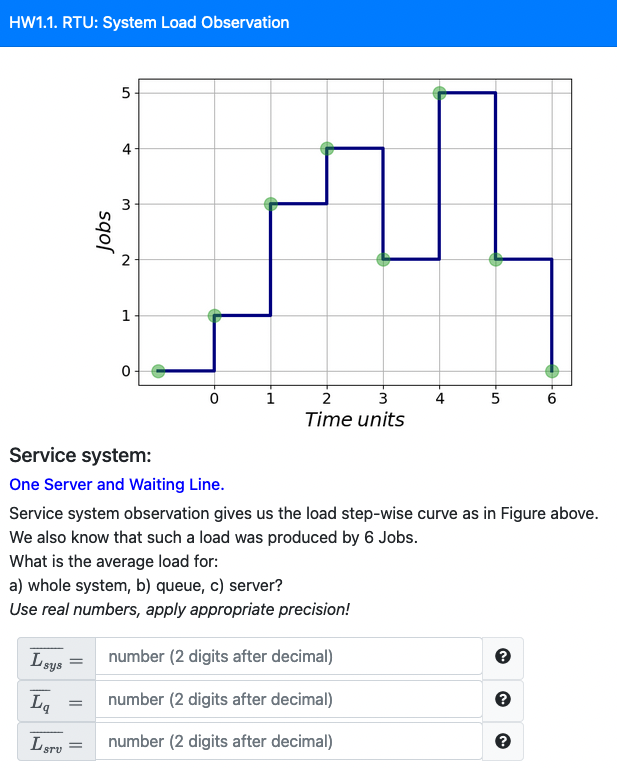
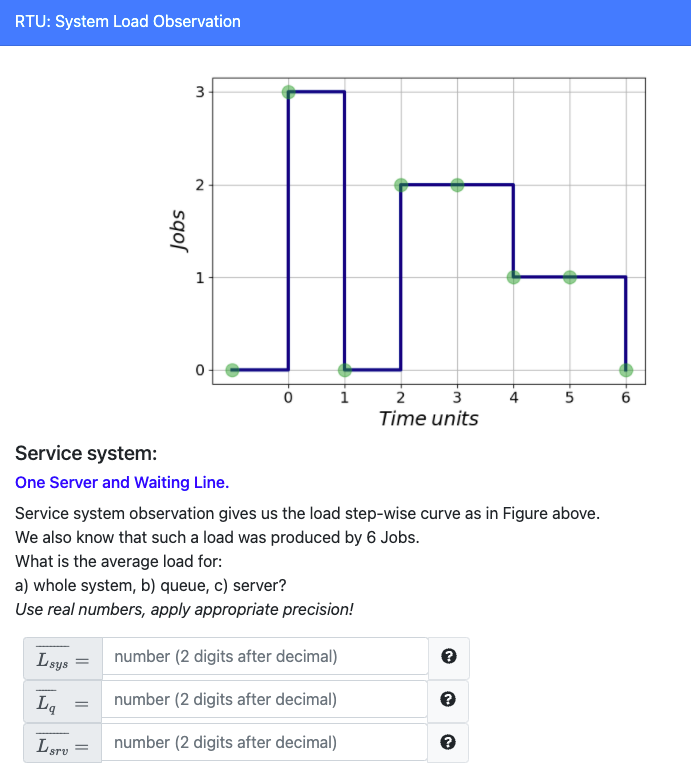
Another viewpoint on load-time model

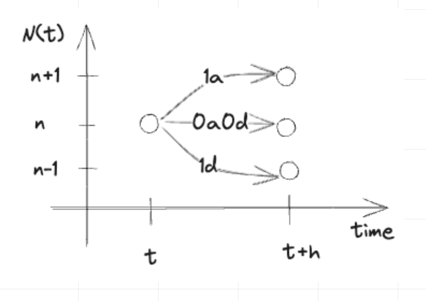
Theoretical Model of a Single Node Service system
In theory, what can you reveal from the model above?
Week 6
Classwork
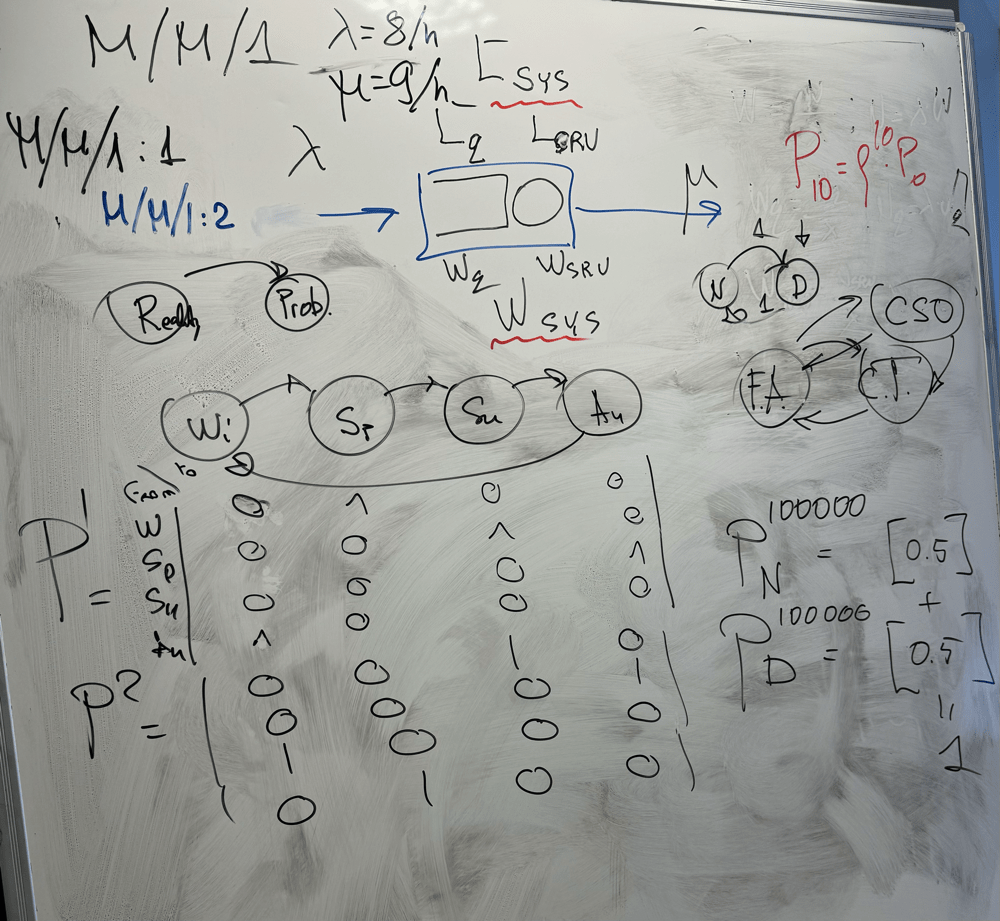
Week 6
Classwork
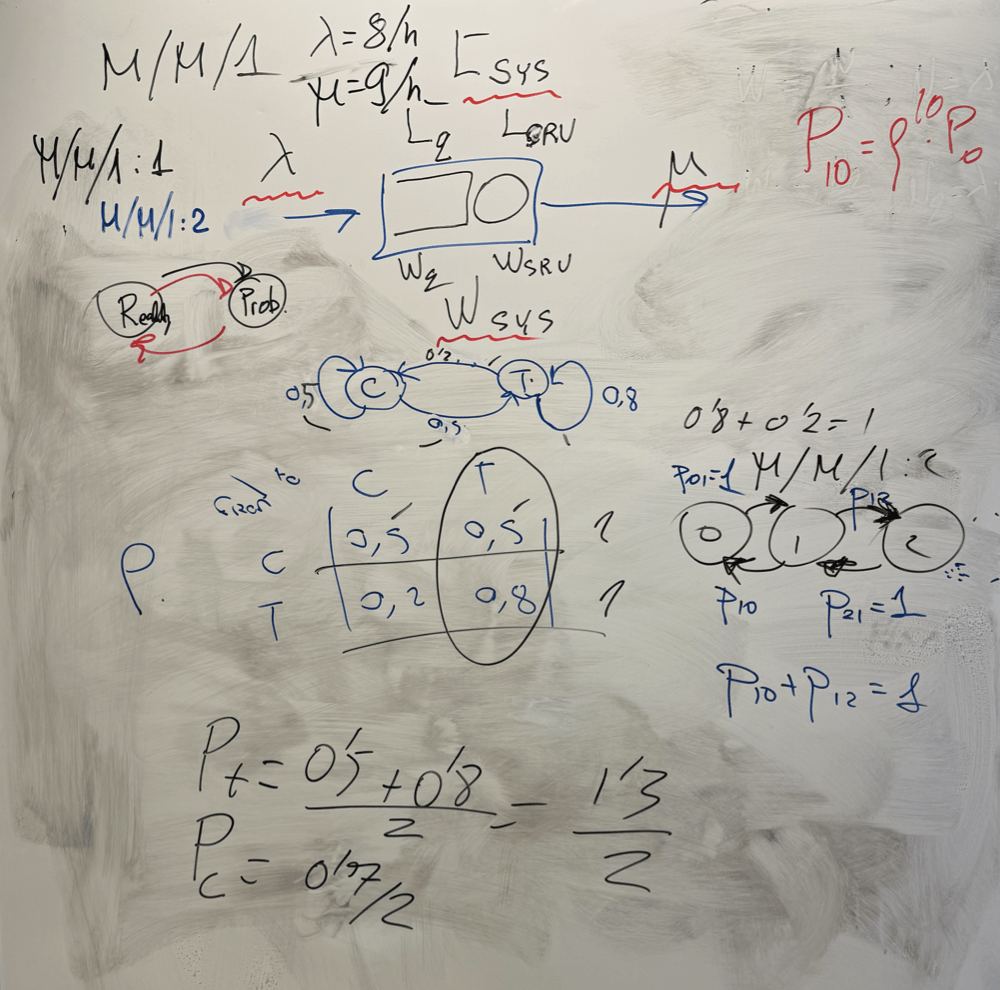
Classwork

Week 6
Week #7
From Observation to Models
2024-03-11


Classwork Time

Week 7
Classwork
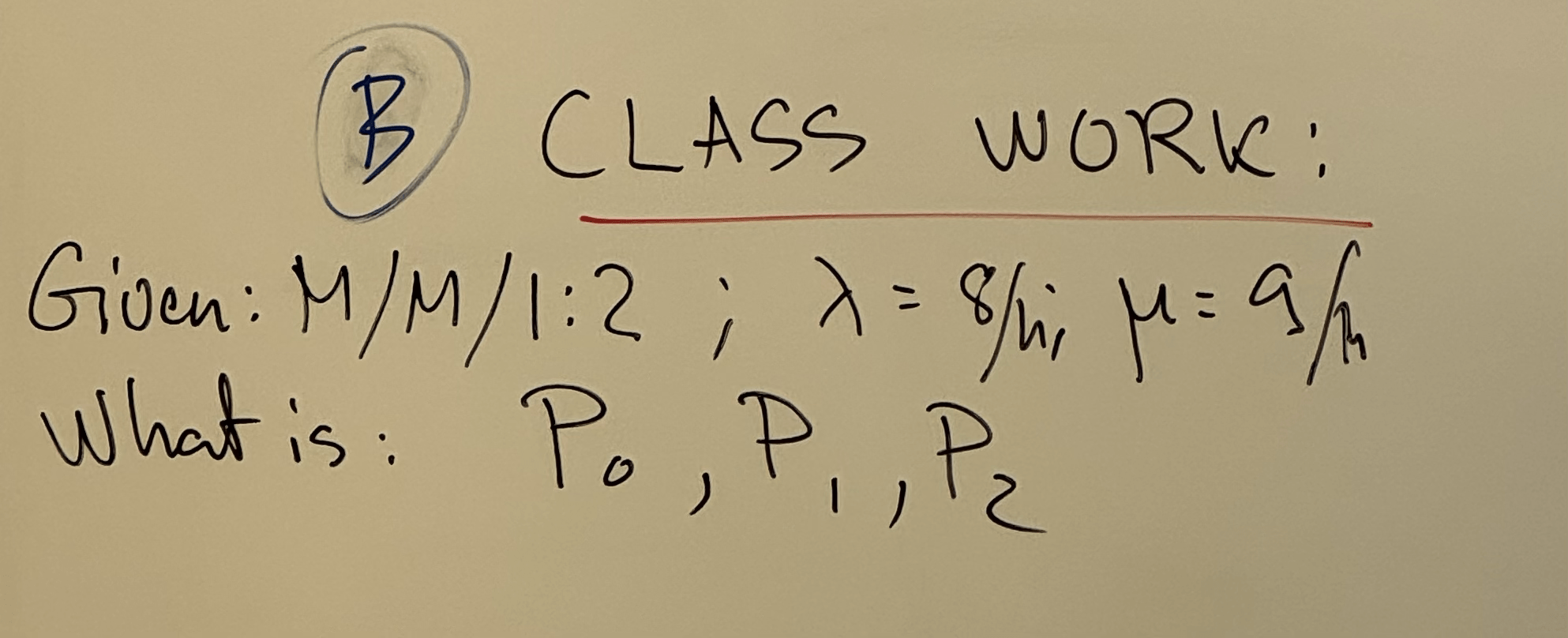
Week 7
Classwork
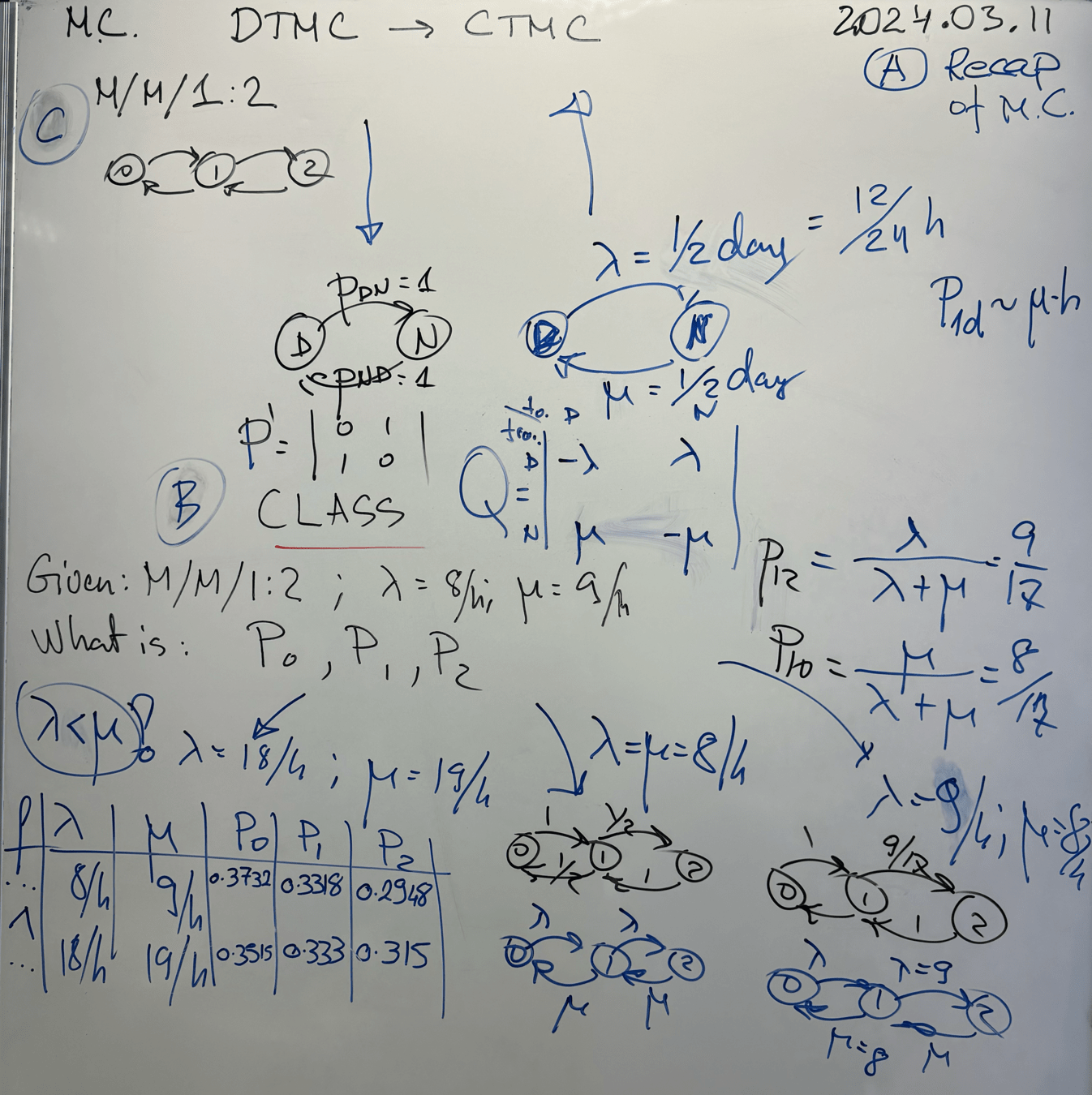
Week 7
Classwork
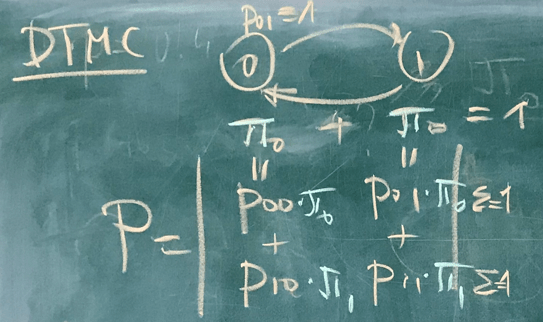
Week 7
Classwork
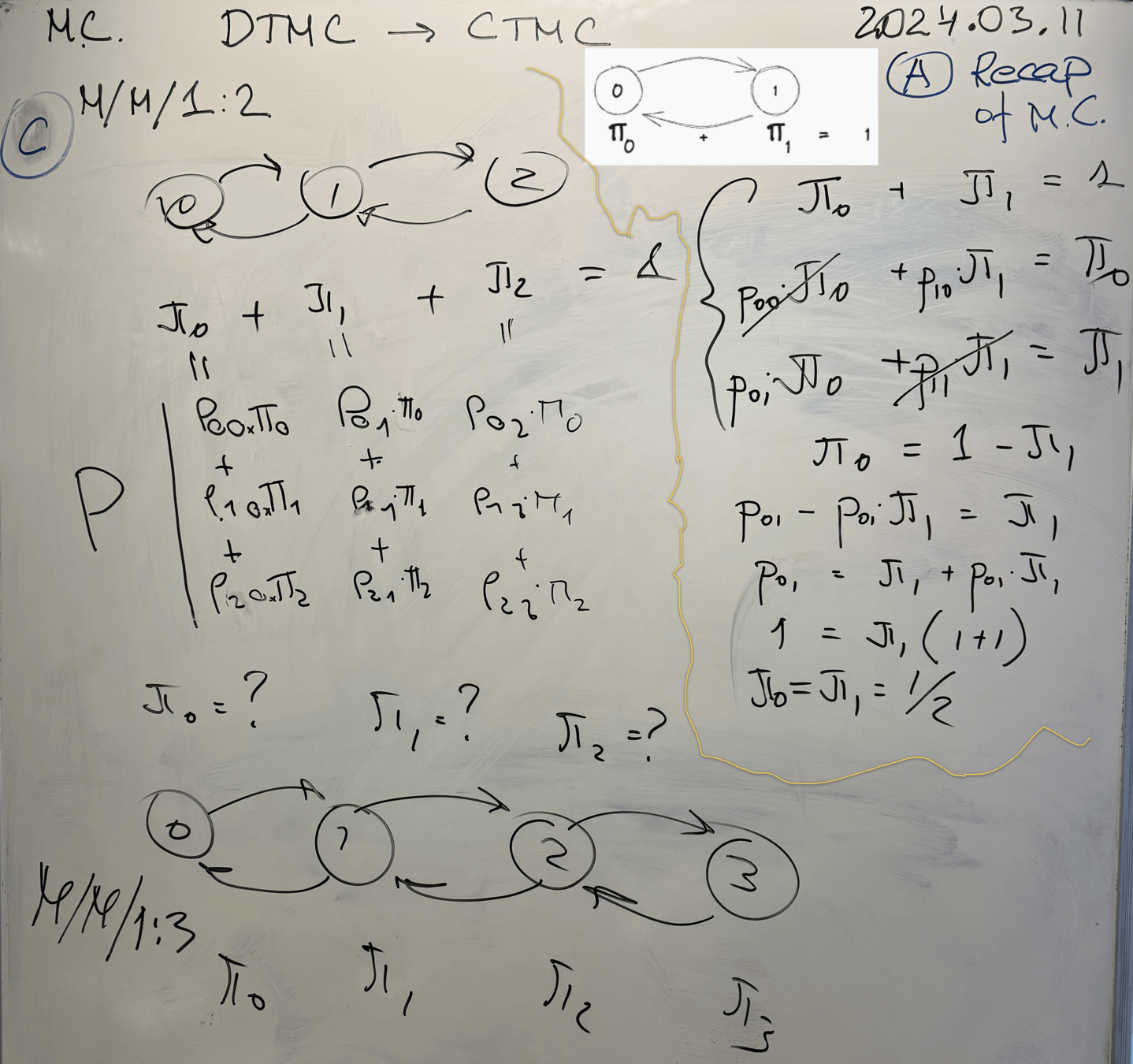
Pre-Class Week 8
Homework - Part 1
Learning Markov Chains


1. Record your voice in AUDIO format, explaining the terms used in the Equation system.
2. Use screen recording to point to the terms you are discussing.
3. Publish your record in the Slack HOMEWORK CHANNEL.
Week #8
Infinite and Finite
2024-03-18

2nd Module Exam
APPROACHING
Theoretical Models
Service Systems
Week #8
From Observation to Models


2024-03-18


https://towardsdatascience.com/sql-joins-a-brief-example-9d015868b56a
https://www.google.com/search?q=andrey+andreyevich+markov&rlz=1C5CHFA_enLV889LV889&sxsrf=APq-WBsyI88xAvtsq7nGDiBEw2fcxhf7gg:1646897947719&tbm=isch&source=iu&ictx=1&vet=1&fir=1mWzaoYlCdvr8M%252Cv3SWMCoFghWAVM%252C%252Fm%252F0kz0%253BfJgqZDzcP0pUaM%252Co_AQCFk0WdmyFM%252C_%253BmBXNaksaj7WQ0M%252C12KOCiPVrIPXPM%252C_%253BmTj0m0tPFcUyKM%252C80KAu9zJ0rx8jM%252C_%253B18svUHl8YhDi9M%252CSgL9fpTCX3B9zM%252C_%253BVplz4lXluhbLiM%252CC613xlUTf5RX7M%252C_%253BElZthqyswocQ-M%252COGOZlLA1jJicWM%252C_%253BWIPpos0yzSuwOM%252C8POXzH7gnQ6F0M%252C_%253BVeyJaCGraCGUDM%252C8POXzH7gnQ6F0M%252C_&usg=AI4_-kR2sk7mcGr3QPtmSzFvW1MvfgN3fA&sa=X&ved=2ahUKEwjp5p35hLv2AhUhR_EDHTAhBhoQ_B16BAgpEAE#imgrc=5hEhbQsA4C8tUM

Week 8
FINITE SYSTEMS
DTMC
(Discrete-Time Markov Chains)
Markov Chains
CTMC
(Continuous-Time Markov Chains)

Challenges




Markov Models


BOOKS

SLIDES
VIDEOS
STACKEXCHANGE

Week 8
FINITE SYSTEMS
DTMC
Markov Chains
CTMC

Week 8
CLASSWORK
DTMC
Learning Markov Chains
OVERVIEW on DTMC

Aperiodic irreducible DTMCs are ergodic since each
has at least one state i with

Demonstration Time

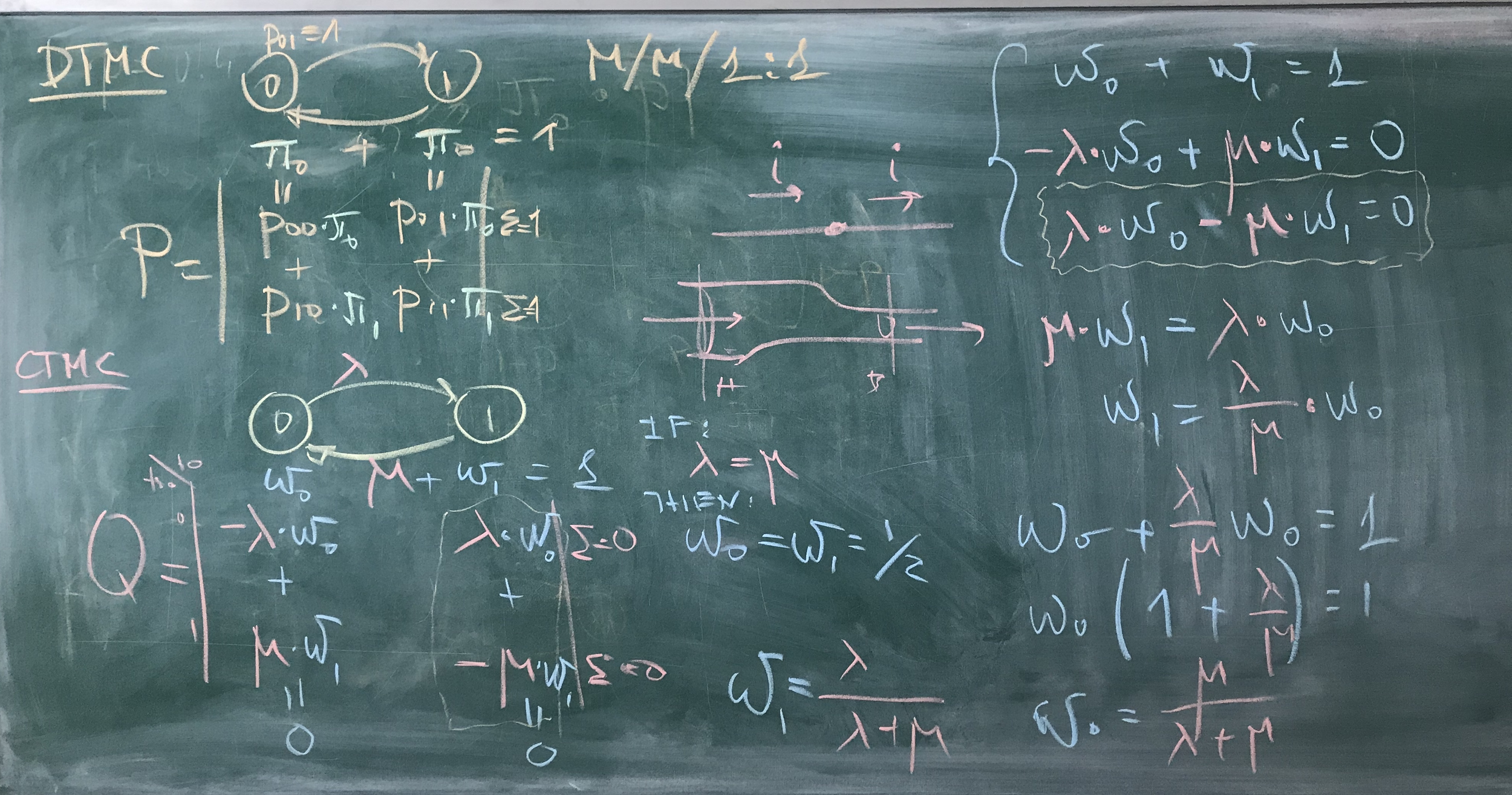
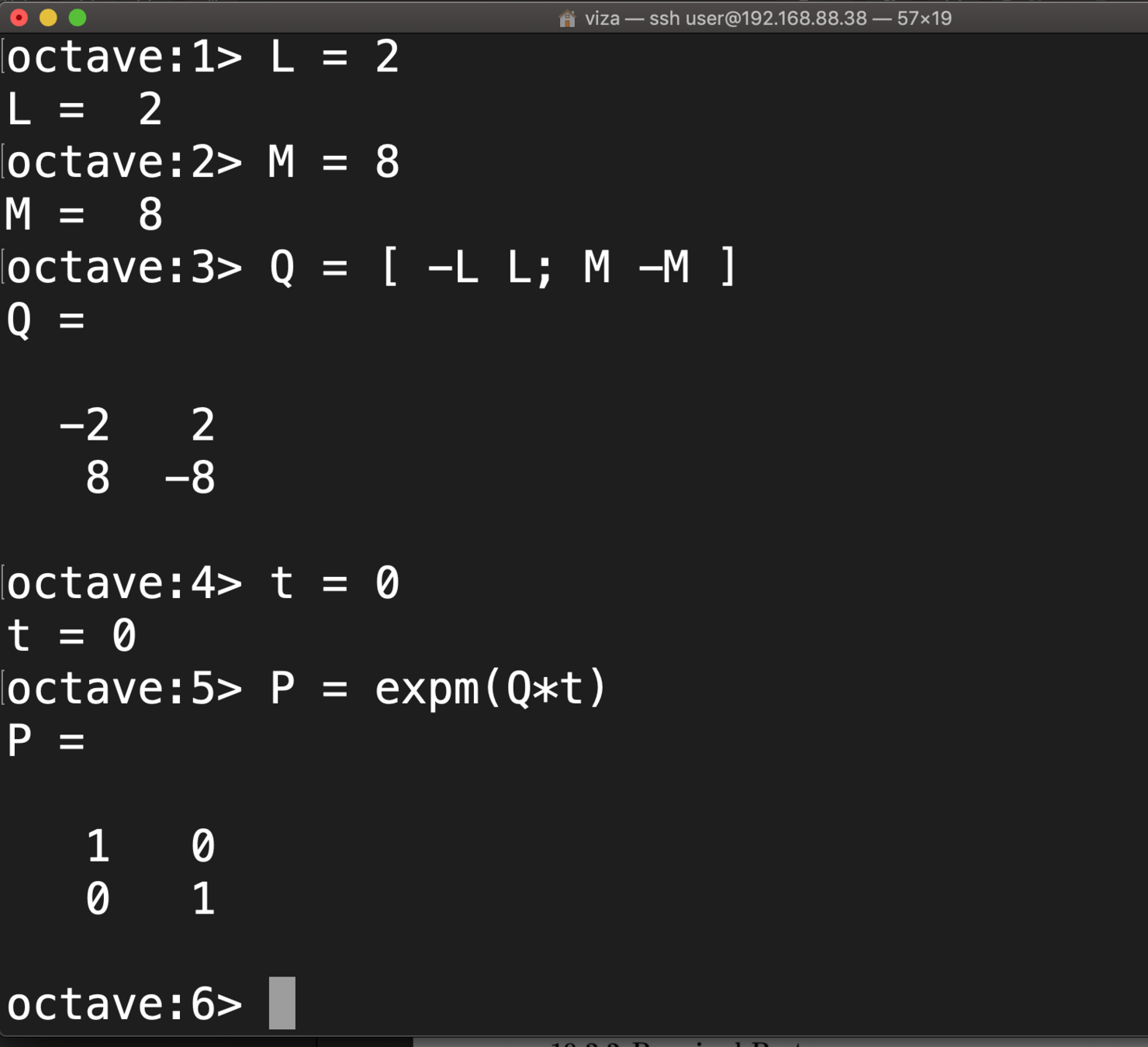
Week 8
DTMC
PROFESSOR-UMBRELLA MODEL
Learning Markov Chains
Classwork
Week 8
Classwork

Week 8
DTMC
Learning Markov Chains
- PROFESSOR has 2 UMBRELLAS
- For example, there is a chance of rain with one umbrella available at home, but even if the rain does, and the professor takes the umbrella to work, he/she will take it back if the precipitation occurs again. One can't take more than one umbrella, so the number of umbrellas varies from walk to walk AND from the weather conditions. But, if there is no rain occurring outdoors, the professor can forget to take an umbrella, like every one of us usually does. So, in the situation, if NO umbrellas are available, the bad (wet) things happen - you can easily guess what.
- Compute and sketch the function of the probability of "getting clothes sodden" in a long term process (let's say - 60 walks) depending on the rain probability

Classwork
Week #9
From Observation to Models
2024-04-08







F.A.S.T.
https://medium.com/big-self-society/jim-kwiks-fast-method-will-help-you-learn-faster-5d3d669dc3b5
method


Week 9
Moving towards Reality

Homework - Part I and II

Learning through Models

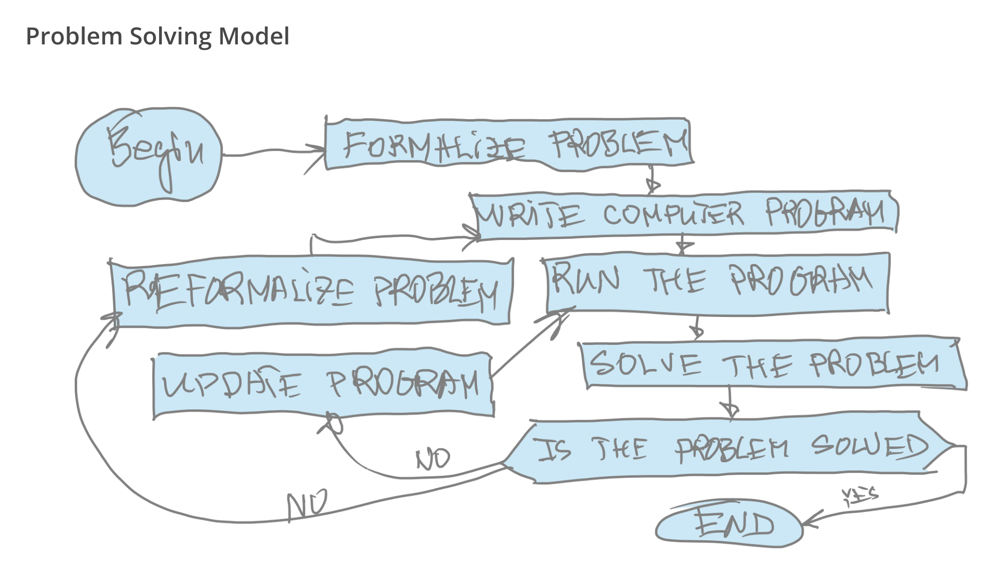
Where is the Key of Problem Solving?

quantitative-model-checking
Week 9
FINITE SYSTEMS
DTMC
(Discrete-Time Markov Chains)
Markov Chains
CTMC
(Continuous-Time Markov Chains)
quantitative-model-checking

Demonstration Time
CTMC
(Continuous-Time Markov Chains)

Quantitative Model Checking
Week 9
Homework - Part I
CTMC
Learning Markov Chains
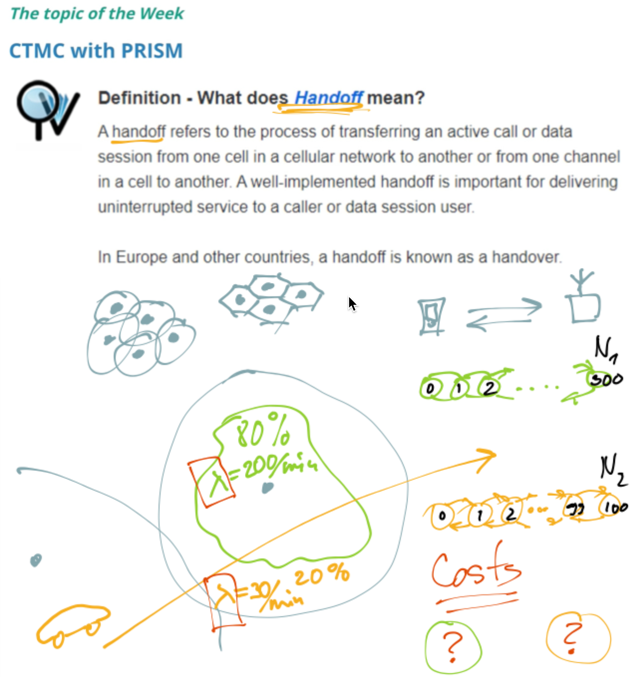
- BARBER-SHOP
- has 2 SEATS and 2 EXTRA WAITING SEATS
- Two BarBERS are operating
- If, ...

https://www.coursera.org/learn/quantitative-model-checking/lecture/DWlJz/definition-of-a-ctmc
quantitative-model-checking
Week 9
Homework - Part II
Demonstrate progress in the course:

https://www.coursera.org/learn/quantitative-model-checking/lecture/DWlJz/definition-of-a-ctmc
quantitative-model-checking

Week #10
From Observations to Models
2024-04-15

to PN
From

Week 9
Homework
Submit Matlab/Octave
code and plots related to BarberShop problem

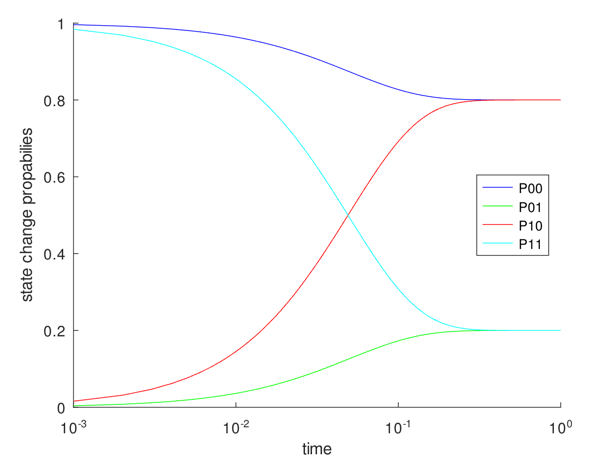
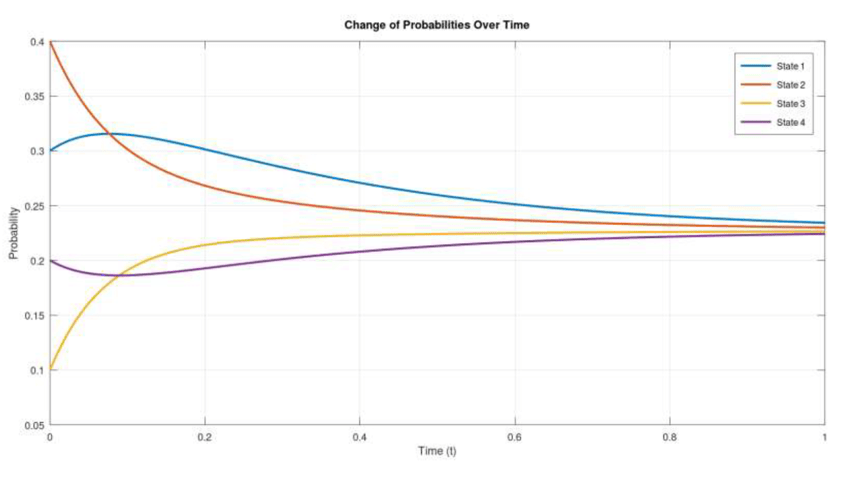
Week 10
Homework - Part I
Get and Install the Snoopy tool
from Cottbus Uni
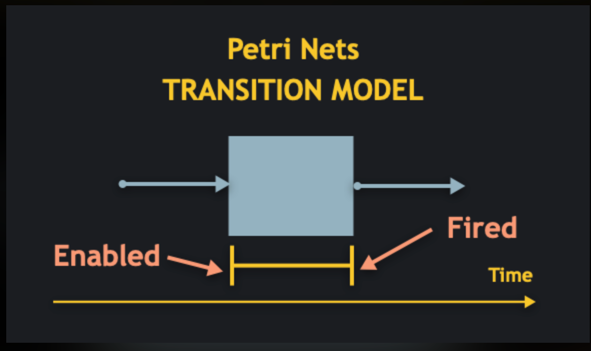
Learning Petri Nets

Demonstration Time
PN
(Petri Nets)

0
1
0
1
MarkovChain
Petri Net
Control Element
State
State
Place
Place
Transition
Transition
State Index
Number of
Tokens

Week 10
Homework - Part II
Using Snoopy
Learning Petri Nets
Transforming MC models
(e.g. BarberShop)
into simple but stochastic Petri Nets

Week #11
From Observations to Models
2024-04-15

to
From

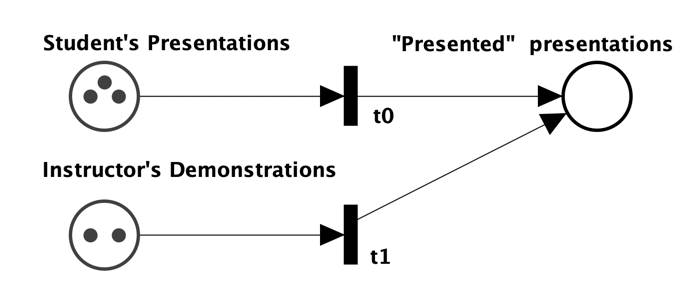

Week 11
Moving towards Reality

Including all Homework Fragments

Demonstration Time
Tokens are on the Students' Court
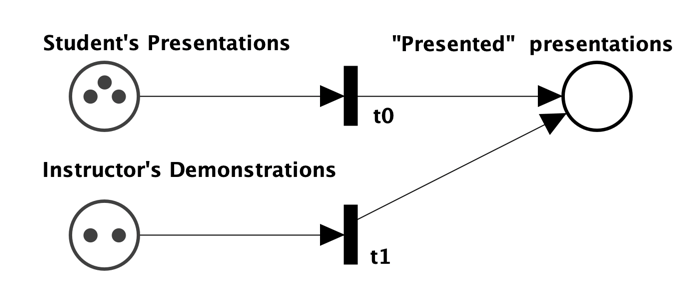

Demonstration Time
The token is on the Instructor's Court


Week 11
Homework - Part I
Learning Petri Nets
Output
- Demonstrate understanding of the topic, and namely,
- Publish a handwritten recap of the lecture examples {Ex.1 .. Ex. 6} with comments
Participate in DELHI UNI Lecture:
Mod-05 Lec-08 Stochastic Petri Nets

Week 11
Homework - Part II
Using Snoopy Tool and STPN Model,
Learning Petri Nets
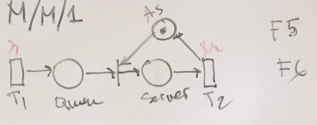
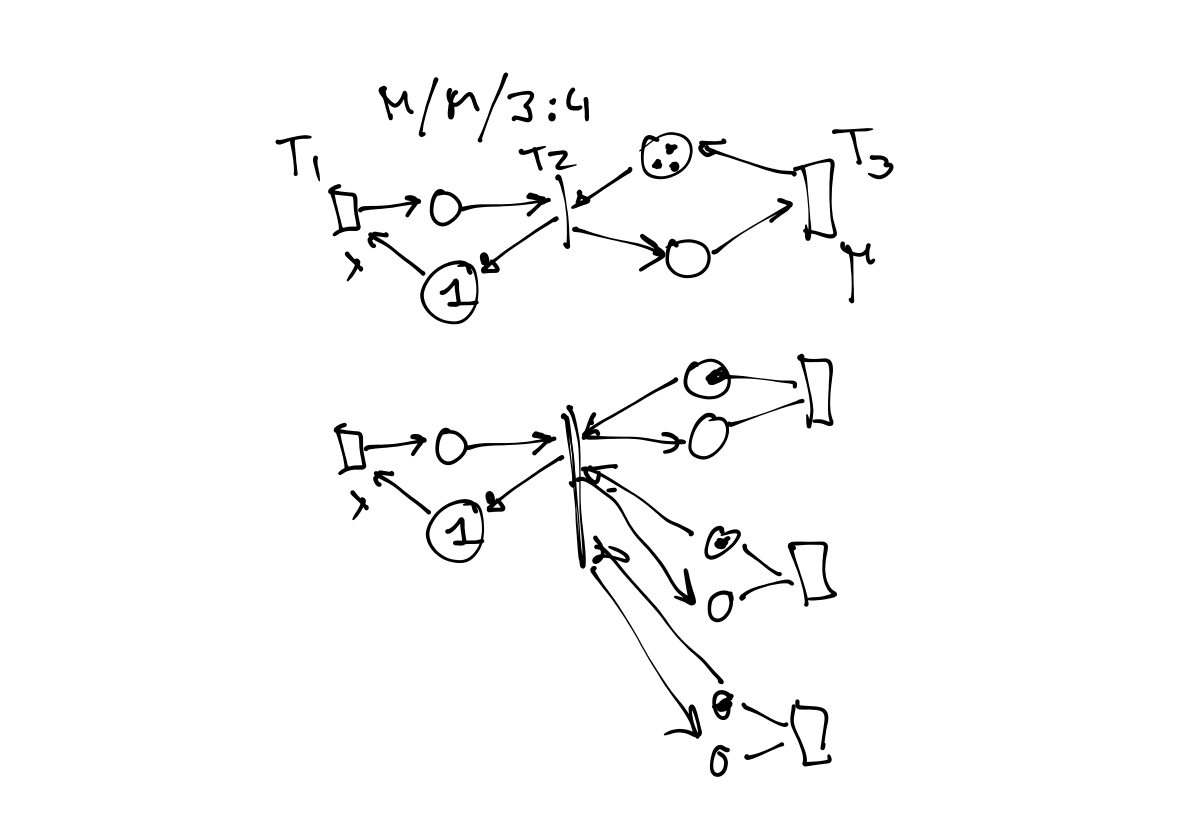
Verify an Algebraic Model for the System M/M/1
through Load and Waiting Time metrics
Output
- On YouTube published Video Report

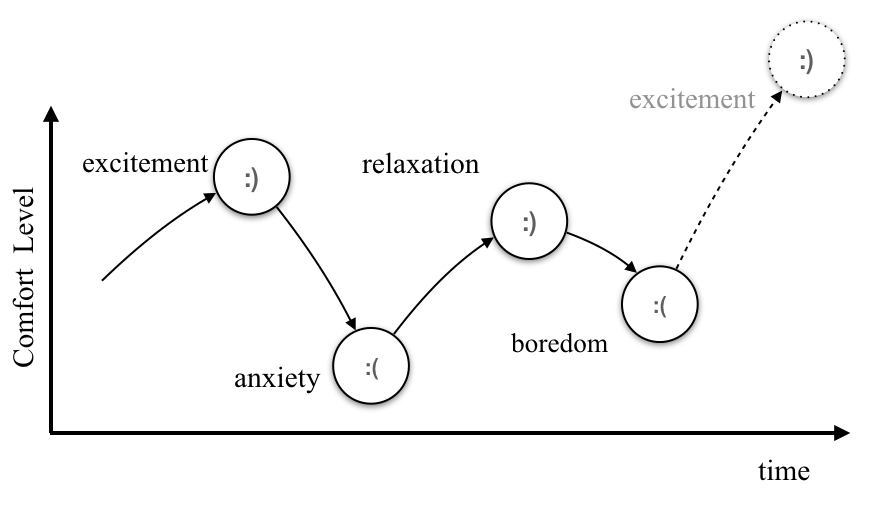
Emotional Cycles
Week 1
Week 2
...
Week13
.END

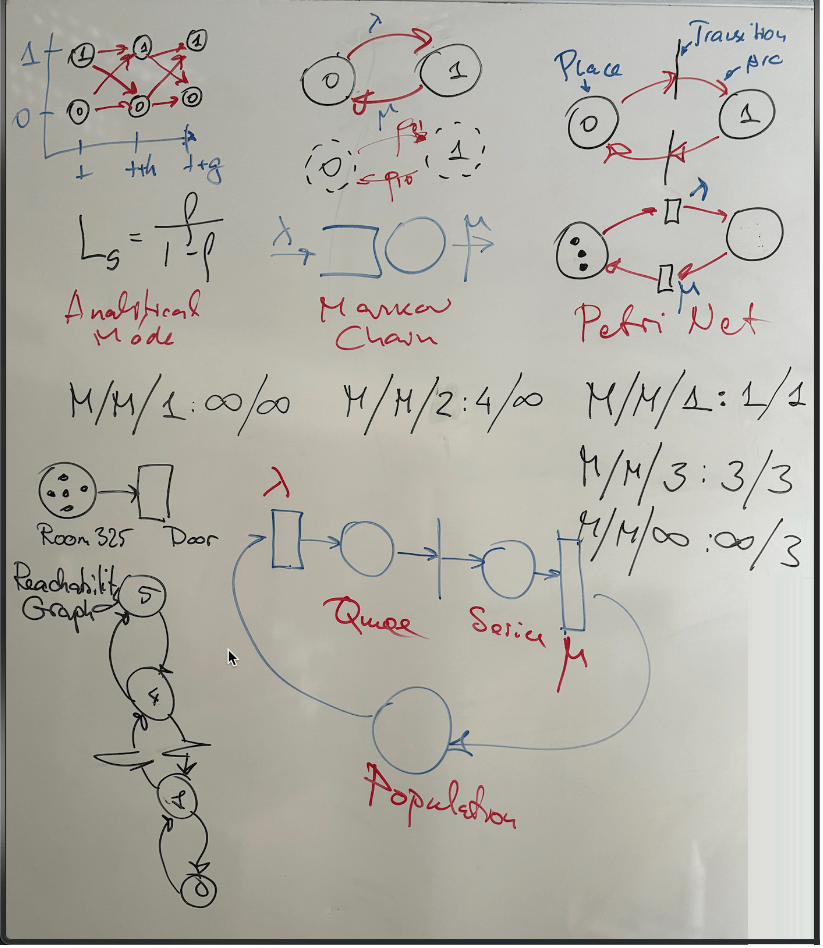
CLASS NOTES
Week #12
From Observations to Models
2024-04-22

to
From



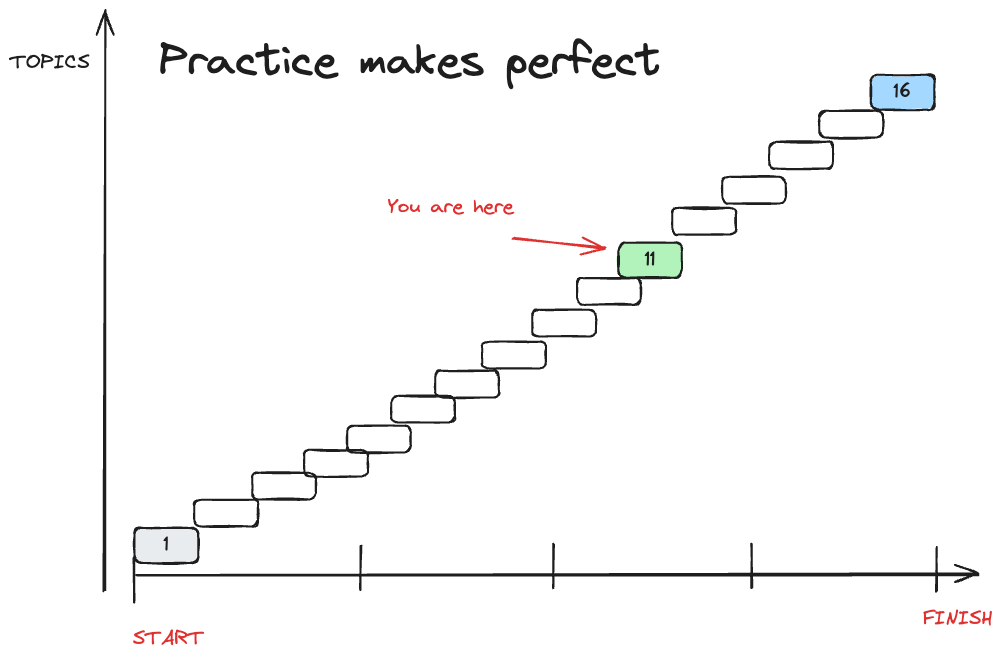
a SEMI-ULTIMATE Tool
Petri Nets in Modelling



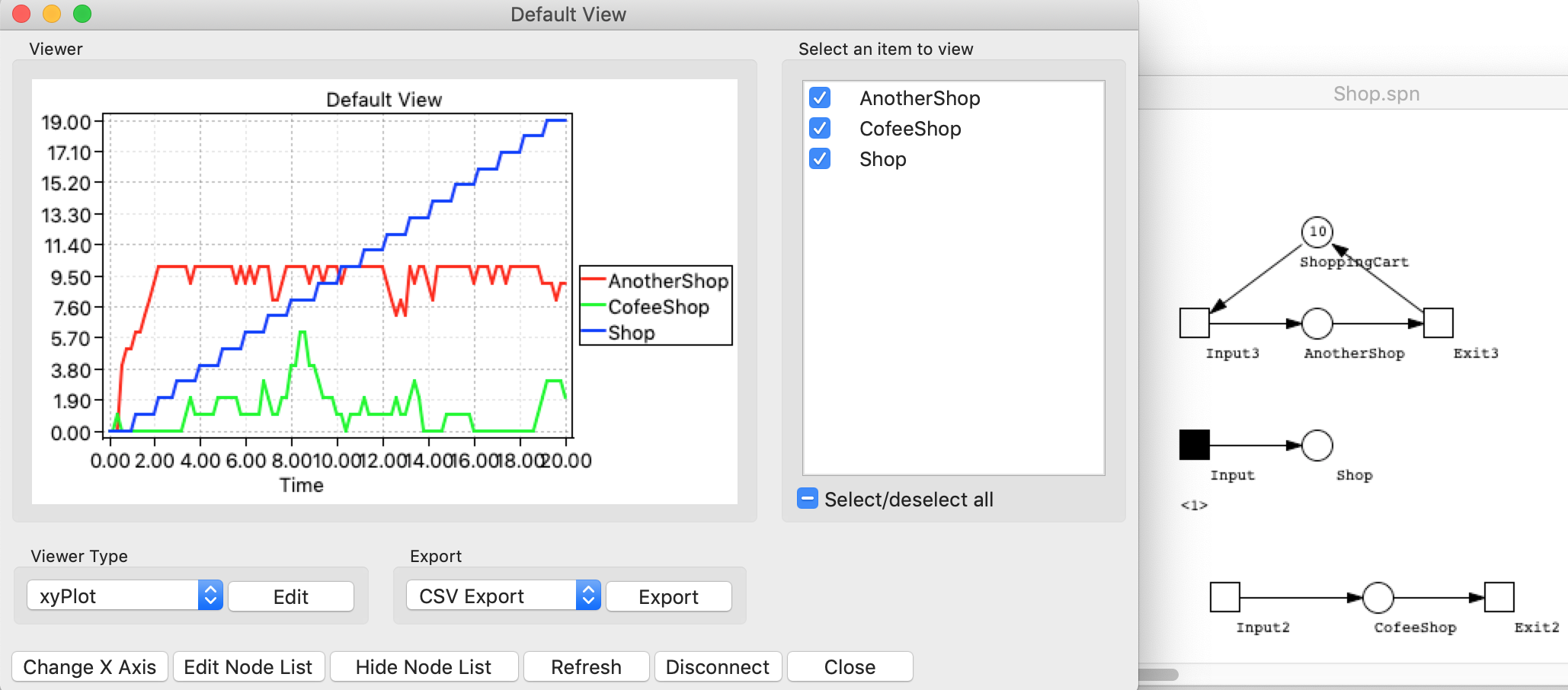






Week 12
TODO: start thinking about the model

BW = 10 Mbps
BW = 100 Mbps
BW = 100 Mbps
queue size?


Volume = {1..10} // Integer [Byte/Packet/Message]
Priority = {Low, High} // Integer
Origin = {1, 2} // Integer
Destination = {1 .. 6} // Integer
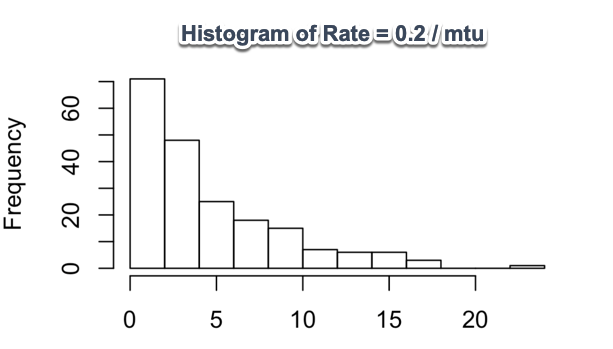
iat = { 12 .. } // Double [1/min]
lambda = { 5 .. } // Double [1/hr]
minQueueLength = {0...N}; // Integer
Server
Client 2
Client 1
Controller
Synchronous
Asynchronous
Asynchronous
Engineering Question: What is a value of








Scientific Research Topics
- e.g. "Verifying theoretical M/M/x:x/x/x models utilising Petri Nets".
- How to make queues, protocols and services better?
- e-mails, notifications, chats, bots, scheduling systems and apps
- authentication, authorisation, etc. protocols
- networking software/hardware, PLC controllers, etc.
- Modelling with Higher-Order Tools
- PRISM Model Checker (from OXFORD UNI),
- UUPAAL
- ns-3,
- Fuzzy Logic Systems,
- ...

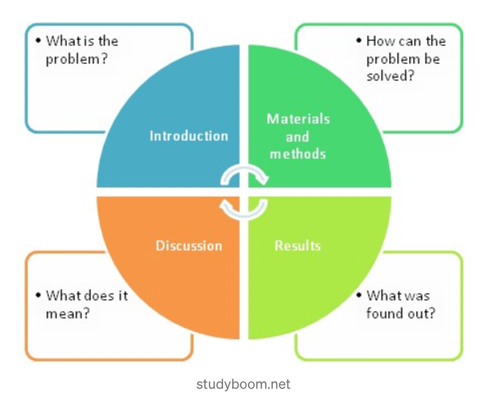
https://medium.com/literacy-discourse/what-does-imrad-reveal-about-science-7de7741ba987
Use IMRAD to demonstrate
Research Results


https://medium.com/literacy-discourse/what-does-imrad-reveal-about-science-7de7741ba987
Use IMRAD to demonstrate
Research Results
“Results are where the findings and the outcomes go.”


Week #13
From Observations to
Approved Models
2024-04-29

AND
VERIFIED BY



MODEL
CHECKER


MODEL
CHECKER

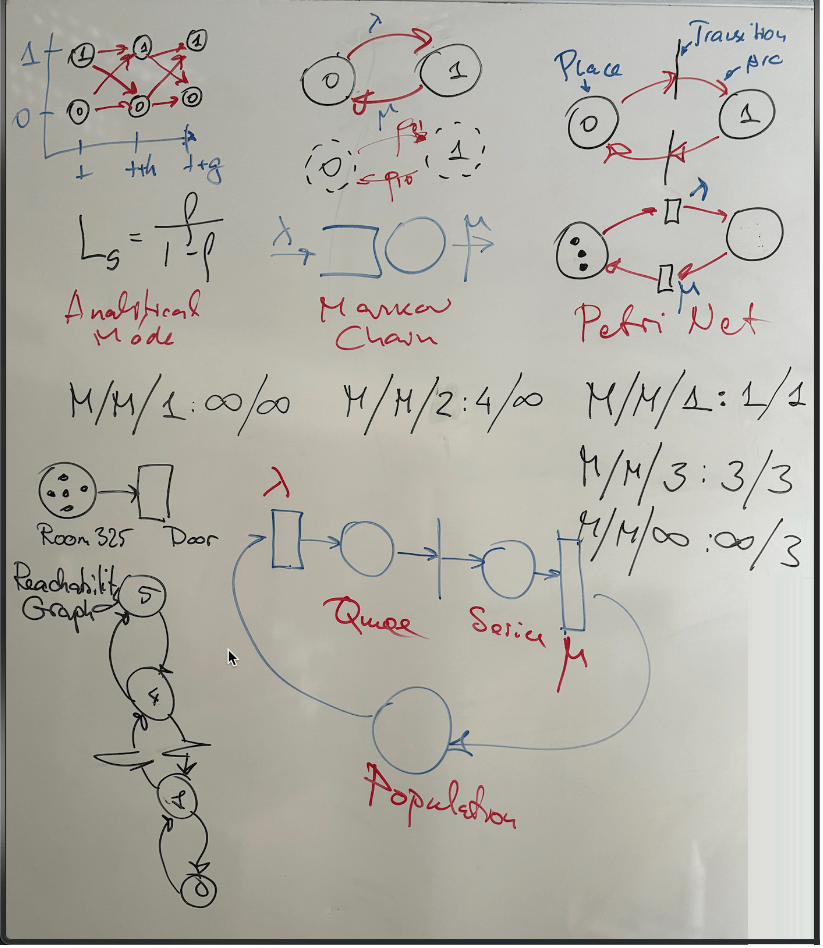
CLASS NOTES
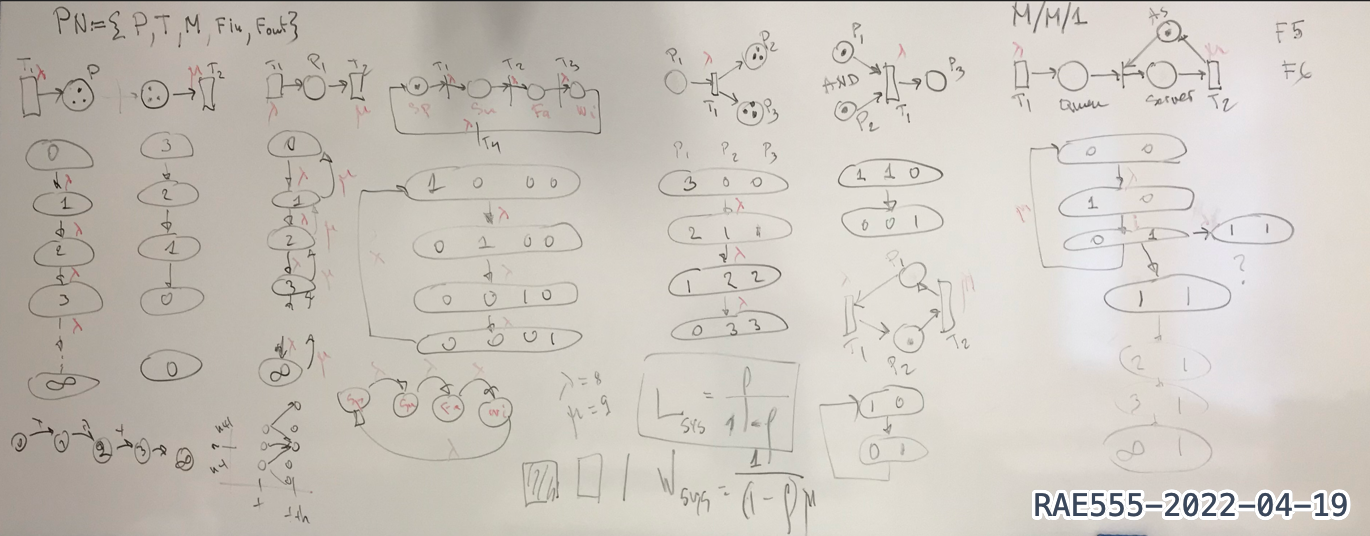

The problem


The problem

The problem
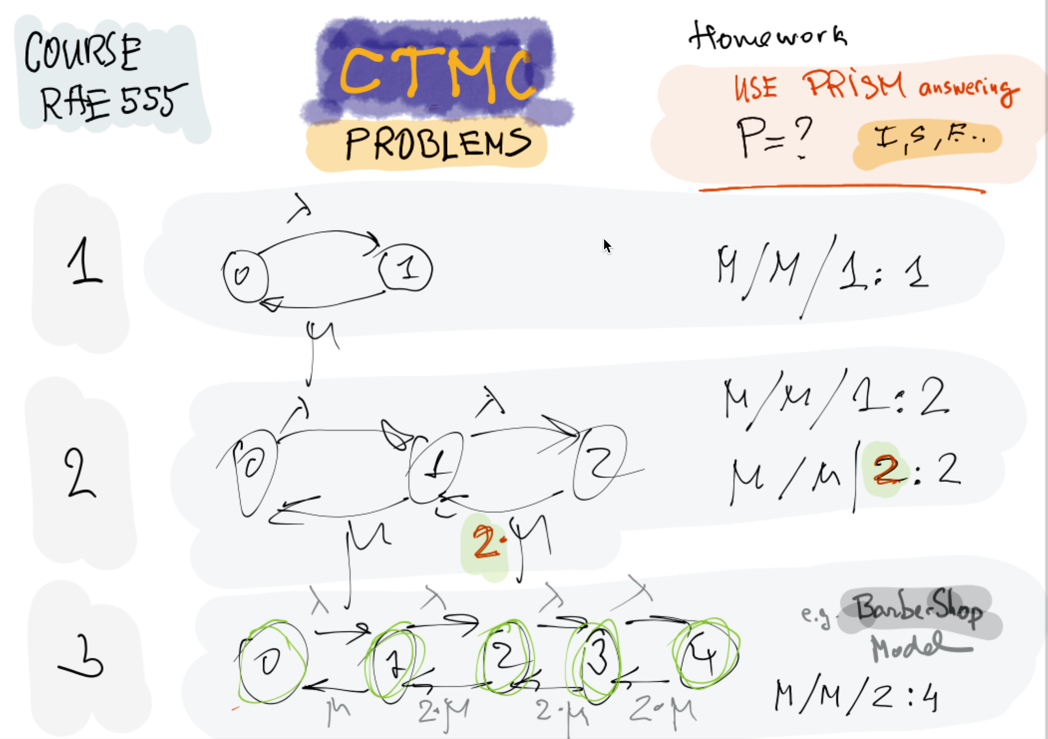

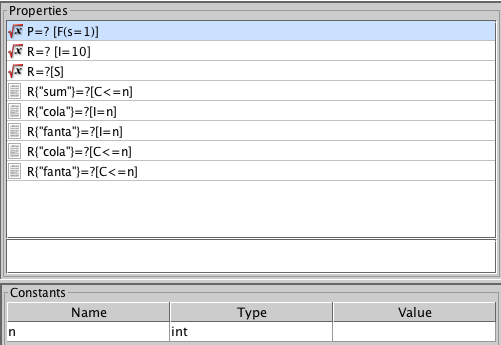
https://www.prismmodelchecker.org/


The problem

THE PROBLEM
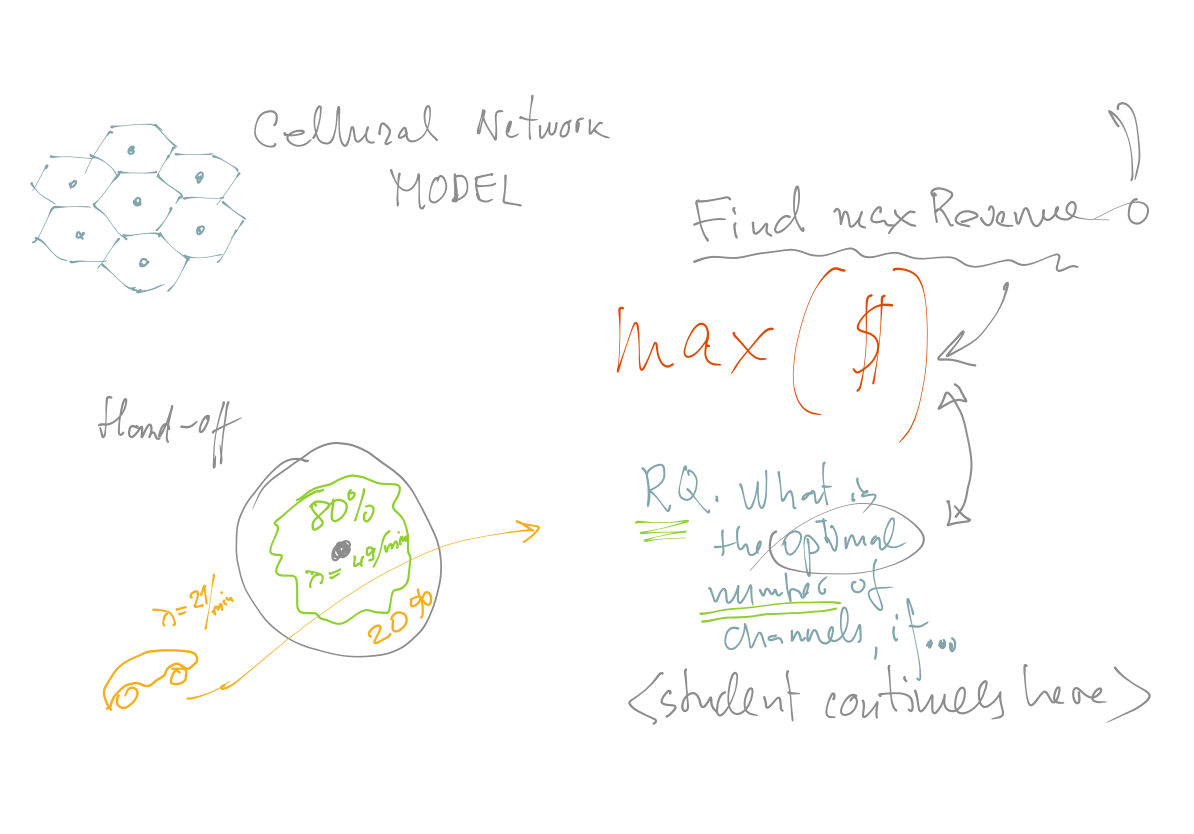
Week 13

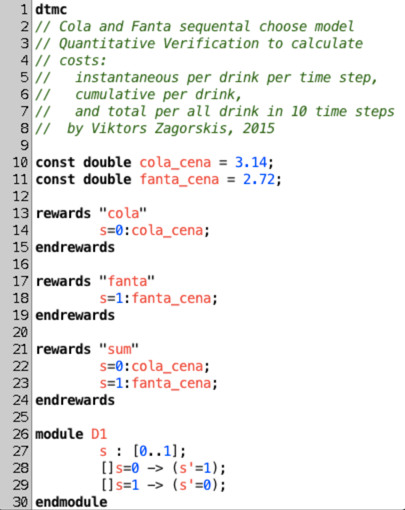
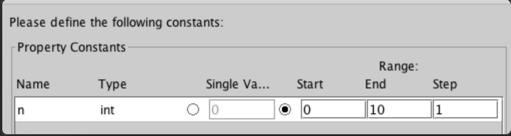
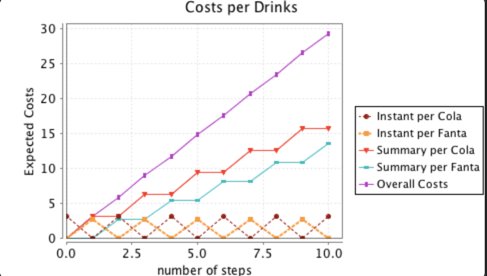
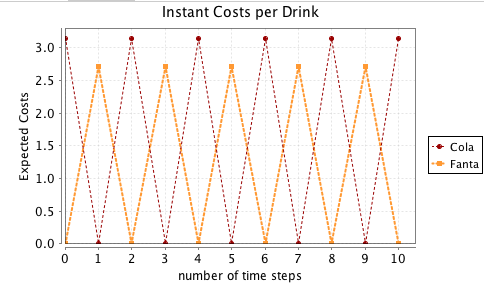

Week 13
Homework
using
PRISM MODEL CHECKER
Verifying Markov Chains
BARBER SHOP MODEL

Week #14
From Observations to
Reliable Models
2024-xx-xx

AND
VERIFIED BY



MODEL
CHECKER


From Observations to
Reliable Models


https://youtu.be/H6vSIM754X4


https://youtu.be/H6vSIM754X4


-
Focus
-
Fundamentals
-
Structure

That kick required is ...
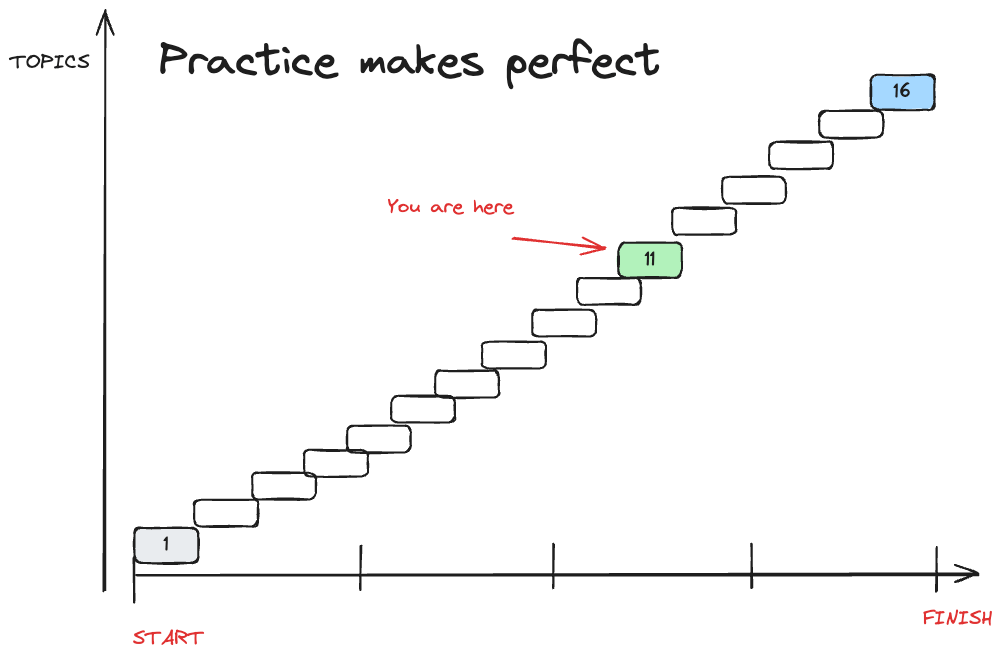
PRACTICE




Demonstration Time
The token is on the Students' Court







Demonstration Time
The token is on the Students' Court

The problem


Demonstration Time
The token is on the Students' Court


Demonstration Time
The token is on the Students' Court


https://www.prismmodelchecker.org/




TODO
Initiate Your Research
Week 16
TODO (PRE-CLASS)
Do research like masters do!

Week 16
TODO (PRE-CLASS)
Volume = {1..10} // Integer [Byte]
Priority = {1 .. 3} // Integer
Origin = {1.. 2} // Integer
Destination = {1 .. 6} // Integer
iat = { 12 .. } // Double [1/min]
lambda = { 5 .. } // Double [1/hr]
Integer minQueueLength = {0...N}; N_max = 1000
Server
Client 2
Client 1
Controller
Synchronous
Asynchronous
Asynchronous

- Studying principles of Traffic Models in Packet-based Network
- Mapping real network observations to empirical Theoretical Models
https://arxiv.org/pdf/1105.1347.pdf

http://www0.cs.ucl.ac.uk/staff/m.handley/slides/nnfn-tcp.pdf
Week 16
TODO (PRE-CLASS)

Demonstration Time
The token is on the Instructor's Court

- Studying principles of Traffic Models in Packet-based Network
- Mapping real network observations to empirical Theoretical Models
Experiments with TCP flow finding an approximating function representing a waiting time for varying amount of data;
e.g. 1KB ... 100MB transferred from Server Instance to Client using 100 Mbps link on local PC machine.
Repeat the experiment, utilizing UDP protocol with up to 8 simultaneous flows.
Prepare video report providing relevant experiment objectives, describing experiment, and presenting code, diagrams, and outcome discussion.
Week 16
TODO (PRE-CLASS)

- Studying principles of Traffic Models in Packet-based Network
- Mapping real network observations to empirical Theoretical Models

Week 16
TODO (PRE-CLASS)

- Studying principles of Traffic Models in Packet-based Network
- Mapping real network observations to empirical Theoretical Models


Week 16
TODO (PRE-CLASS)

- Studying principles of Traffic Models in Packet-based Network
- Mapping real network observations to empirical Theoretical Models



Week 16
TODO (PRE-CLASS)

Volume = {1..10} // Integer [Byte]
Priority = {1 .. 3} // Integer
Origin = {1.. 2} // Integer
Destination = {1 .. 6} // Integer
iat = { 12 .. } // Double [1/min]
lambda = { 5 .. } // Double [1/hr]
Integer minQueueLength = {0...N}; N_max = 1000
Server
Client 2
Client 1
Controller
Synchronous
Asynchronous
Asynchronous
Week 16
TODO (PRE-CLASS)


Volume = {1..10} // int [Byte]
Priority = {1 .. 3} // int
Origin = {1.. 6} // int
Destination = {1 .. 6} // int
iat = { 12 .. } // Double [1/min]
lambda = { 5 .. } // Double [1/hr]
BW = 1 bps
BW = 100 bps
BW = 100 bps
int minQueueLength = 0;
Week 16
TODO (PRE-CLASS)


BW = 10 Mbps
BW = 100 Mbps
BW = 100 Mbps
queue size?
ns-3
Week 16
TODO (PRE-CLASS)


queue size?
REAL NETWORK
Week 16
TODO (PRE-CLASS)

TODO
Week 16
TODO (PRE-CLASS)
Reflection on another Research


Week #15
From Passive Observation
to Wise Action
2024-05-13
F.A.S.T.

with

F.A.S.T.

do Forget
be Active
find the State
Teach the others
Jim Kwik

EXAM
time
It's about




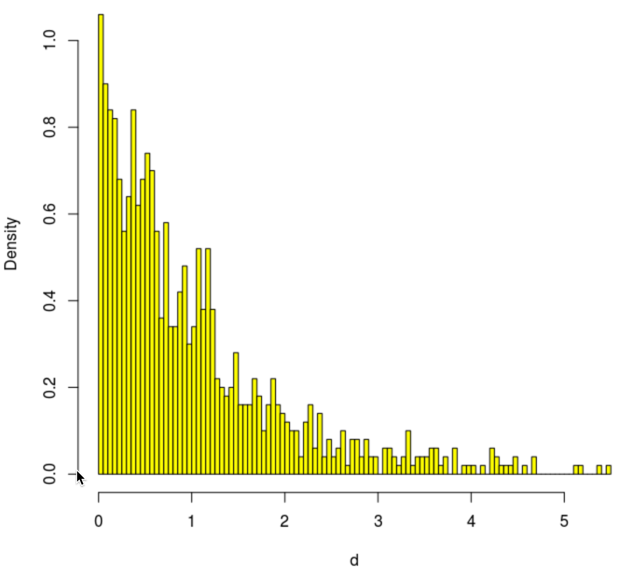

Week 15
Homework - part I
with
PRISM MODEL CHECKER
Verifying
ANY
Queueing Model

Week 15
Homework - part II
with
Rabbit-MQ
Running, Validating and Verifying
ANY
Queueing Model

That kick required to become FAST is ...
PRACTICE





PRACTICE PARADIGM
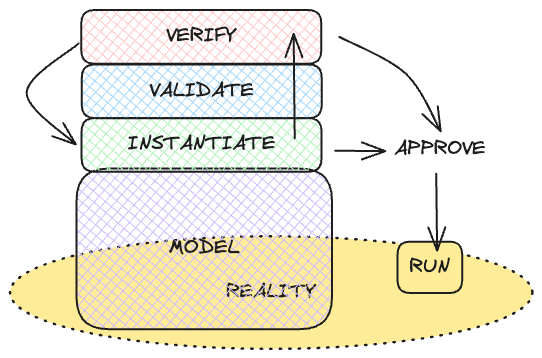
What is Rabbit-MQ ?
https://www.rabbitmq.com/
One broker to queue them all
What is Rabbit-MQ ?
https://www.rabbitmq.com/
One broker to queue them all

RabbitMQ is a reliable and mature messaging and streaming broker, which is easy to deploy on cloud environments, on-premises, and on your local machine. It is currently used by millions worldwide.
Simplest BROKER
WORK QUEUES
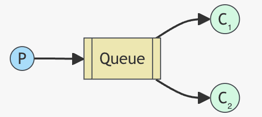
Competing Consumers pattern
WORK QUEUES
Publish/Subscribe pattern
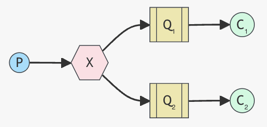
ROUTING
Receiving messages selectively
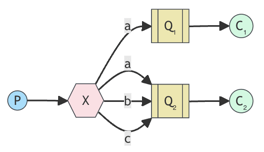
TOPICS
Receiving messages based on a pattern (topics)
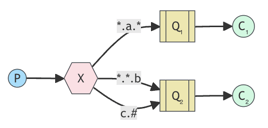
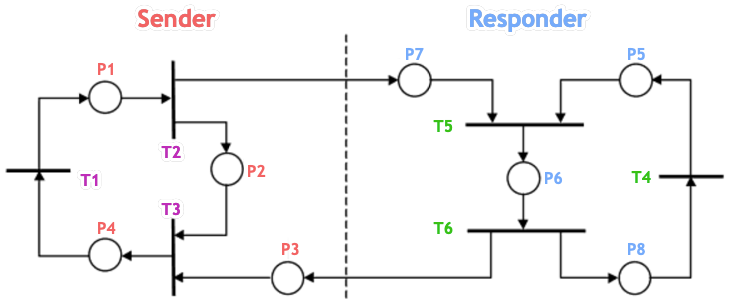
RPC
Request/Reply pattern
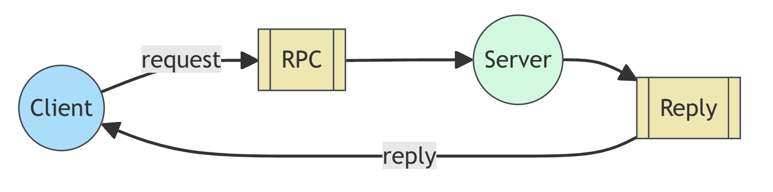
RPC
Request/Reply pattern
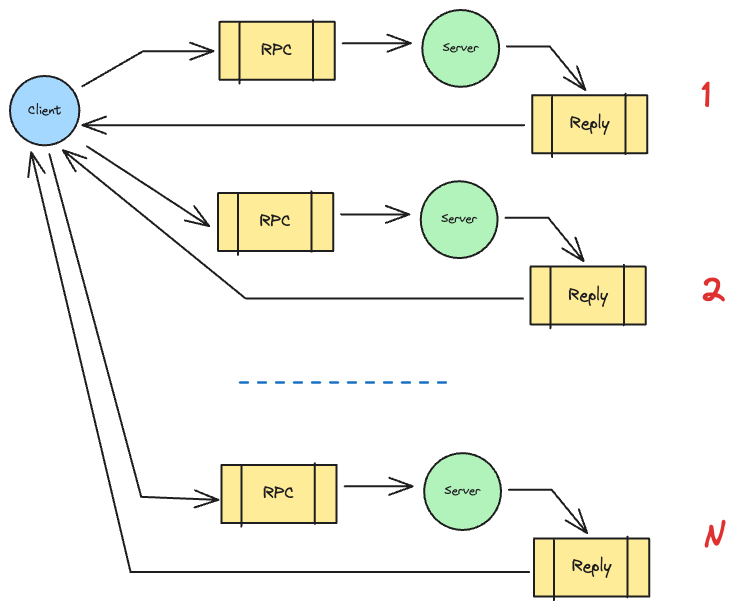
Week 15
Homework - part II
with Rabbit-MQ
Running, Validating and Verifying
ANY
Queueing Model

It's time to demonstrate your skills and competence in
PRACTICE






RABBIT MQ
EXAM TIME

Week 16
EXAM TIME

Week 17
EXAM TIME

Week 17
"What did you learn in RAE 555?"
The course staff would love to hear about what you learned this semester.
What were some highlights?
It would be best to publish your story and all personal materials produced during the course on a static WEB site on
VERCEL or NETLIFY.
End of EXAM TIME

Week 18
FINISH