Learning From Corrupt Data
Sept 11, 2025
Adam Wei
Agenda
- Book-keeping Items
- Improved performance
- Scaling Issues
- "Locality Experiment"
Book-Keeping Items
- Co-training paper was accepted to "Making Sense of Data in Robotics," CoRL
- Other projects
- Pushing for ICRA...
- Privacy project!
Part 1
Sweeps and Performance Improvements
Project Outline
North Star Goal: Train with internet scale data (Open-X, AgiBot, etc)
Stepping Stone Experiments:
- Motion planning
- Sim-and-real co-training (planar pushing)
- Cross-embodied data (Lu's data)
- Bin picking
Last Time: How to choose \(\sigma_{min}\)
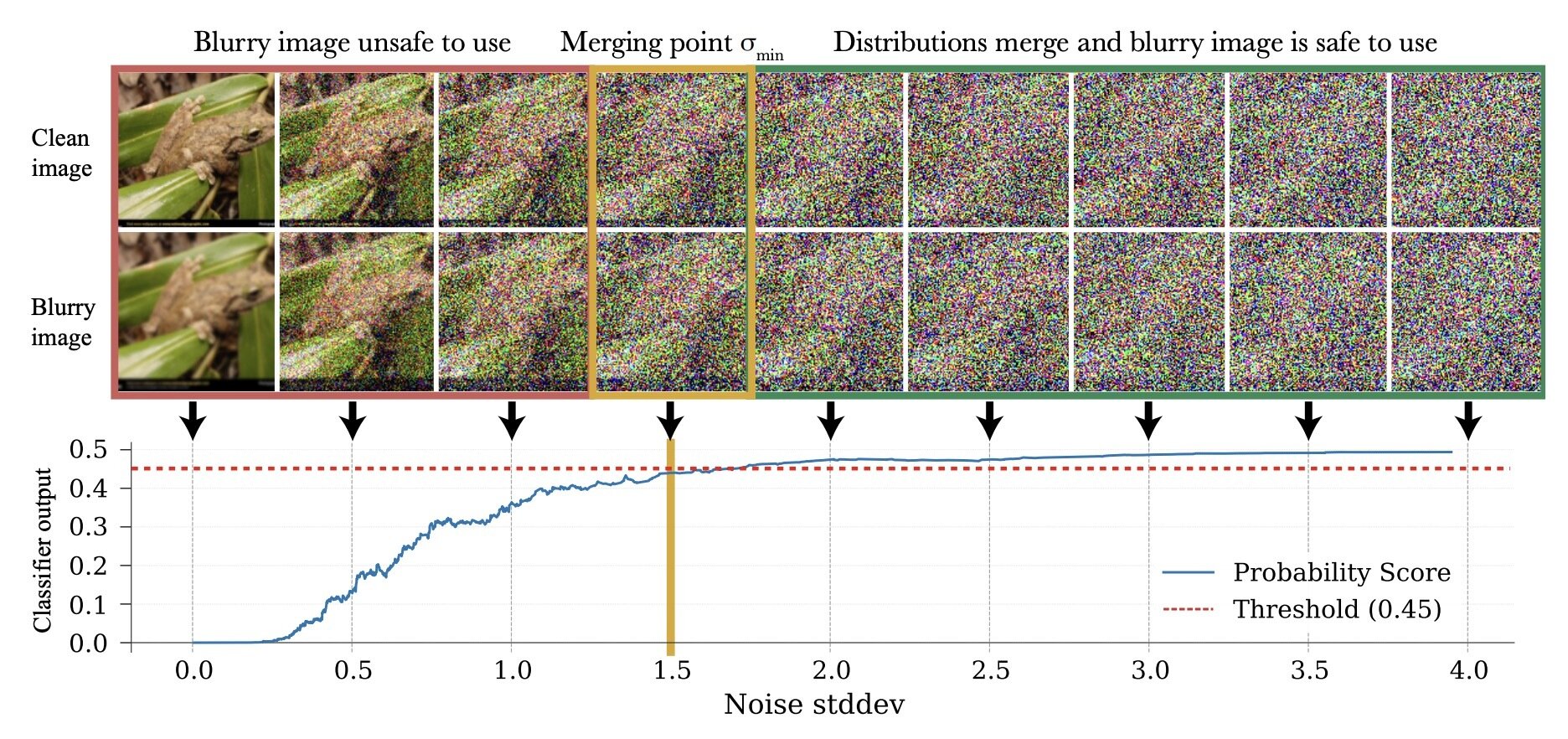
\(\sigma_{min}^i = \inf\{\sigma\in[0,1]: c_\theta (x_\sigma, \sigma) > 0.5-\epsilon\}\)
\(\implies \sigma_{min}^i = \inf\{\sigma\in[0,1]: d_\mathrm{TV}(p_\sigma, q_\sigma) < \epsilon\}\)*
* assuming \(c_\theta\) is perfectly trained
Last time: Which Classifier To Use?
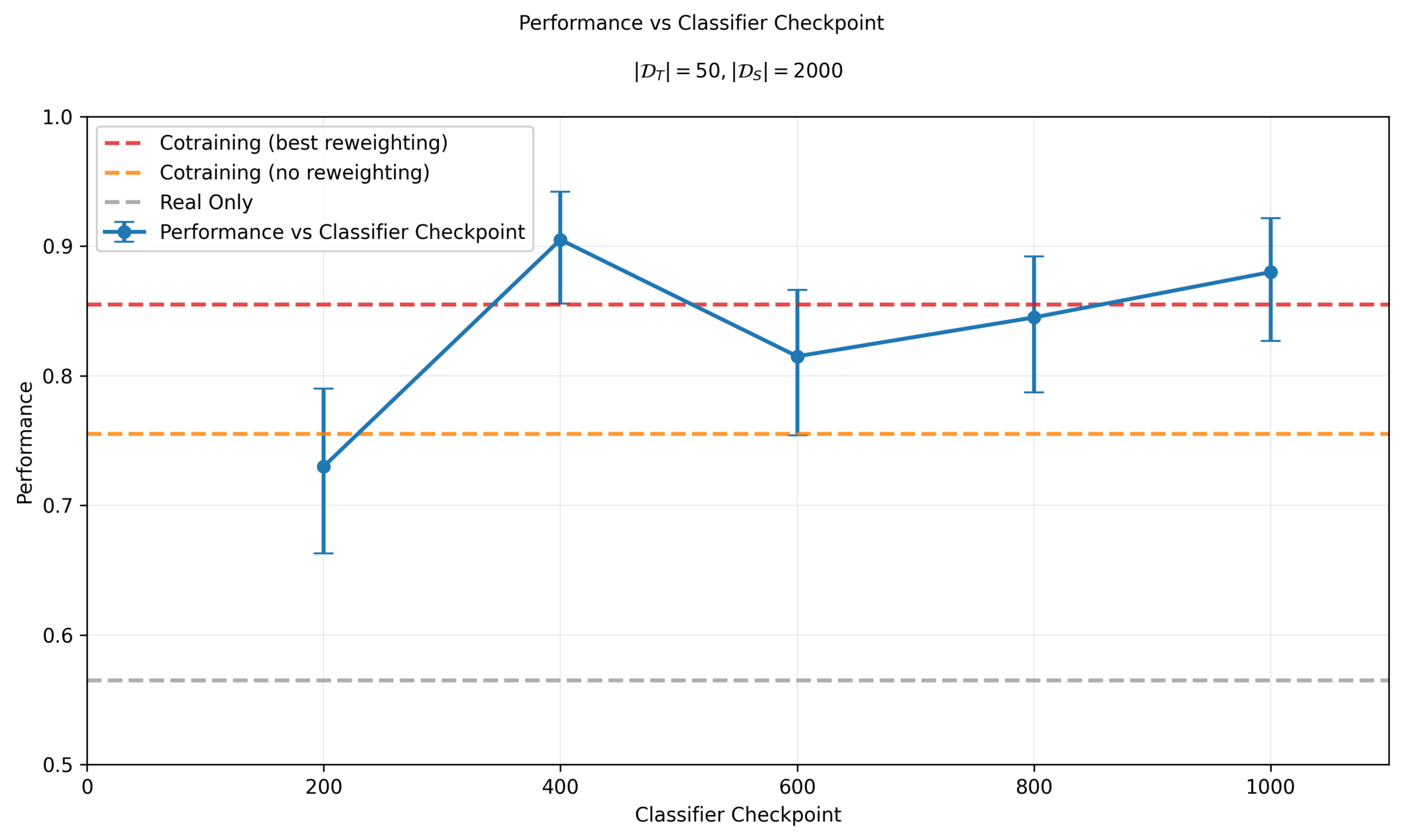
Performance is sensitive to classifier and \(\sigma_{min}\) choice!
Sim & Real Cotraining
Performance vs Classifier Epoch
Sim & Real Cotraining
Choosing \(\tau = 0.5-\epsilon\)

\(\sigma_{min}^i = \inf\{\sigma\in[0,1]: c_\theta (x_\sigma, \sigma) > 0.5-\epsilon\}\)
\(\implies \sigma_{min}^i = \inf\{\sigma\in[0,1]: d_\mathrm{TV}(p_\sigma, q_\sigma) < \epsilon\}\)*
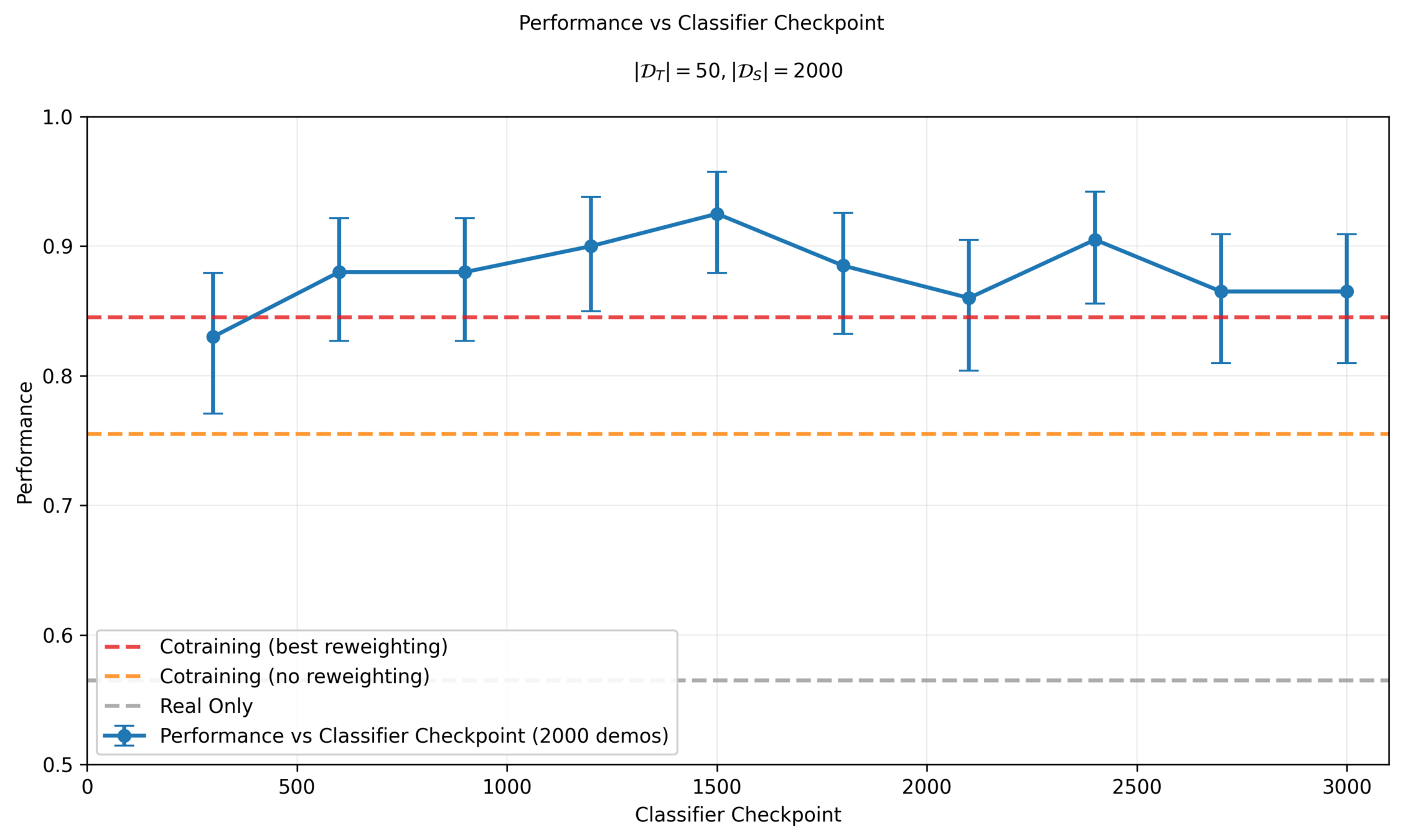
Sim & Real Cotraining
Performance vs Classifier Threshold
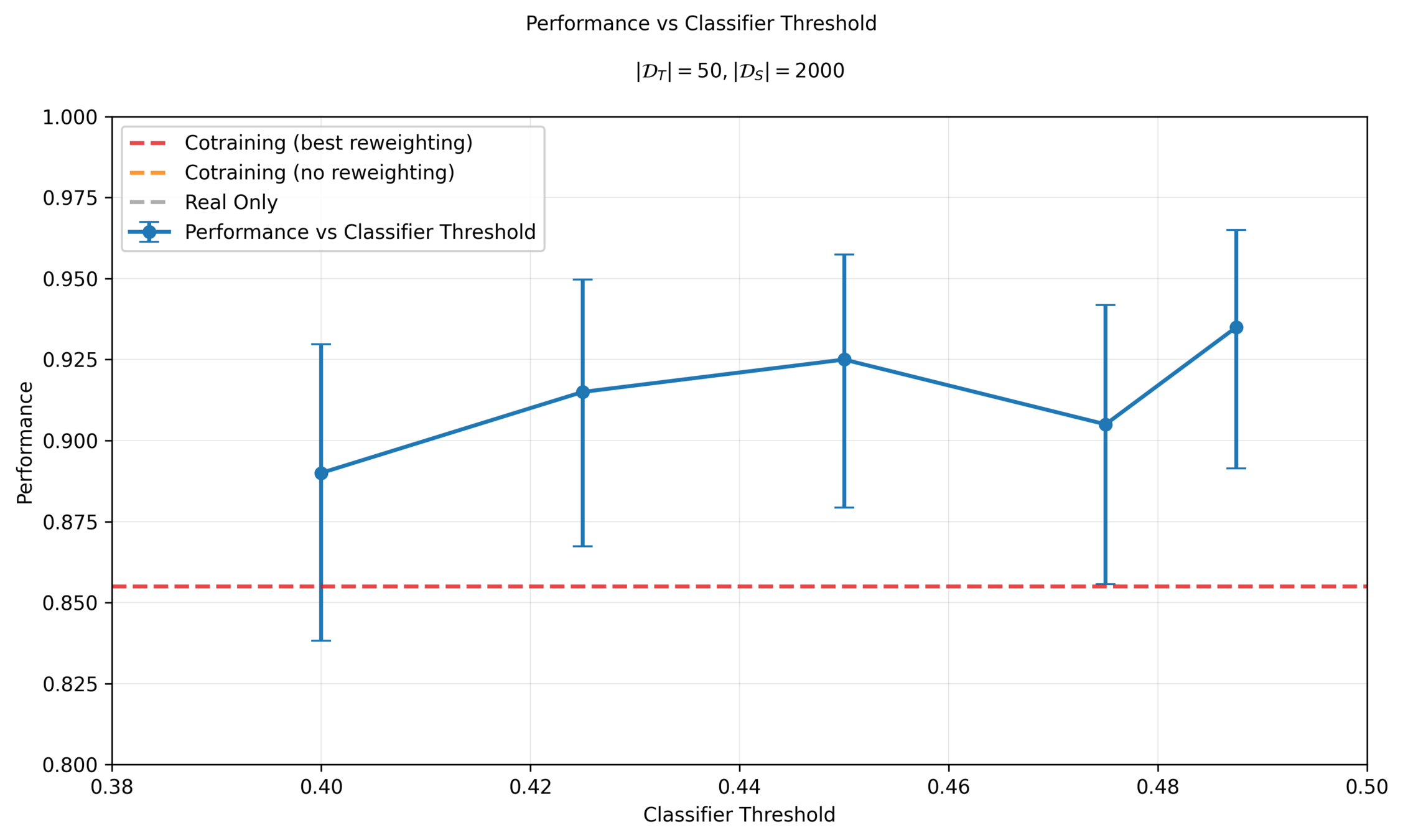
Sim & Real Cotraining
Performance vs Classifier Threshold
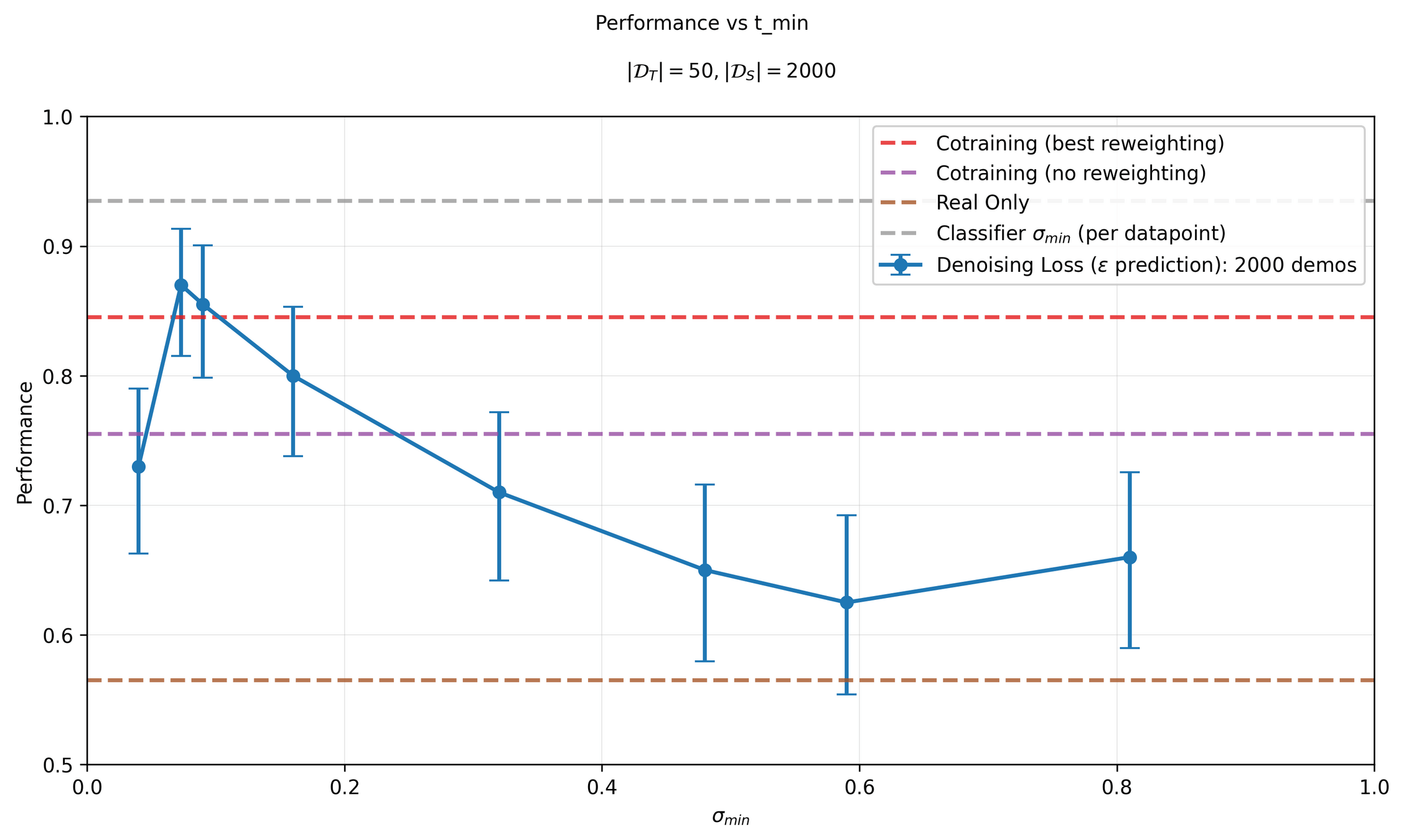
Sim & Real Cotraining
Performance vs Sim Demos: 10 Real Demos

Sim & Real Cotraining
Performance vs Sim Demos: 50 Real Demos

Part 2
Scaling and Algorithmic Issues
Denoising Loss vs Ambient Loss
Ambient Diffusion: Scaling \(|\mathcal{D}_S|\)
Hypothesis: As sim data increases, ambient diffusion approaches "sim-only" training, which harms performance.
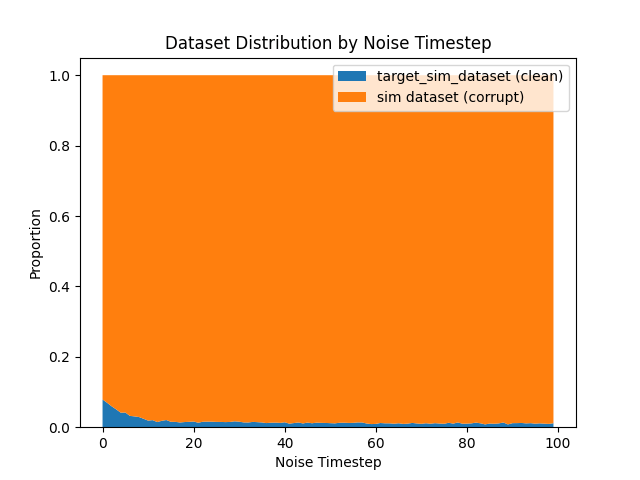
\(|\mathcal{D}_S|=500\)
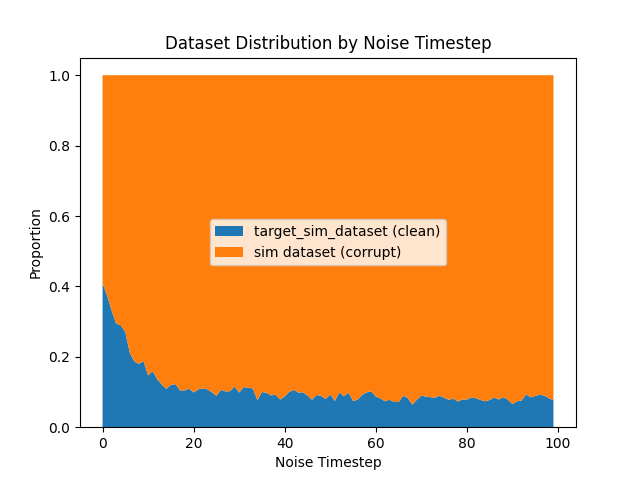
\(|\mathcal{D}_S|=4000\)
Denoising Loss vs Ambient Loss
Ambient Diffusion: Scaling \(|\mathcal{D}_S|\)
Thought experiment
\(\mathcal{X} = \{-1, 0, 1\}\)
Choosing \(\sigma_{min}\) per dataset
Classifier assigns some \(\sigma_{min}\) to all datapoints from \(q_0\)
\(p_0\) samples 0 and 1 w.p. 0.5
\(q_0\) samples -1 and 0 w.p. 0.5
Choosing \(\sigma_{min}\) per datapoint
Classifier assigns \(\sigma_{min}=0\) to all 0's in \(q_0\) and \(\sigma_{min}=1\) to all -1's
\(\implies\) model sees more 0's during training \(\implies\) heavily biased model!
Denoising Loss vs Ambient Loss
Possible Solutions
Choosing \(\sigma_{min}\) per "bucket"
- Split dataset into N buckets (ex. randomly)
- Assign \(\sigma_{min}\) per bucket
- "Can't do statistics with n=1" - Costis
"Soft" Ambient Diffusion
- Instead of having a hard \(\sigma_{min}\) cutoff, use a softer version
- Need to figure out what this soft "mixing" function looks like
- Some theoretical ideas here... WIP
Part 3
Locality and \(\sigma_{max}\)
Denoising Loss vs Ambient Loss
Locality Experiments
Ambient Diffusion: "use low-quality data at high noise levels"
Ambient Diffusion Omni: "use OOD with local similarity at low noise levels"
Intuition
- Real-world data exhibits "locality"
- At low-noise levels, diffusion uses a "small receptive field"
Therefore, we can use OOD data to learn local features at low noise levels
Denoising Loss vs Ambient Loss
Locality


Which photo is the cat?
Denoising Loss vs Ambient Loss
Locality


Which photos is the cat?

Denoising Loss vs Ambient Loss
Locality


Which photo is the cat?
Denoising Loss vs Ambient Loss
Locality



Denoising Loss vs Ambient Loss
Locality
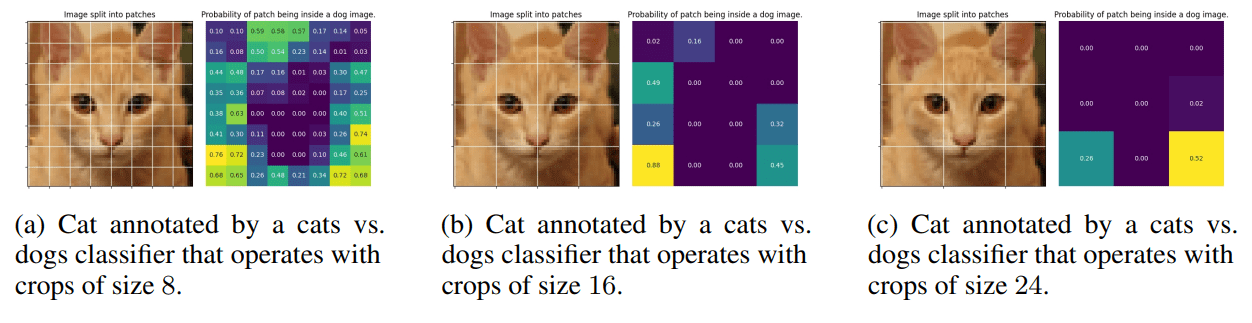
Denoising Loss vs Ambient Loss
Receptive Field
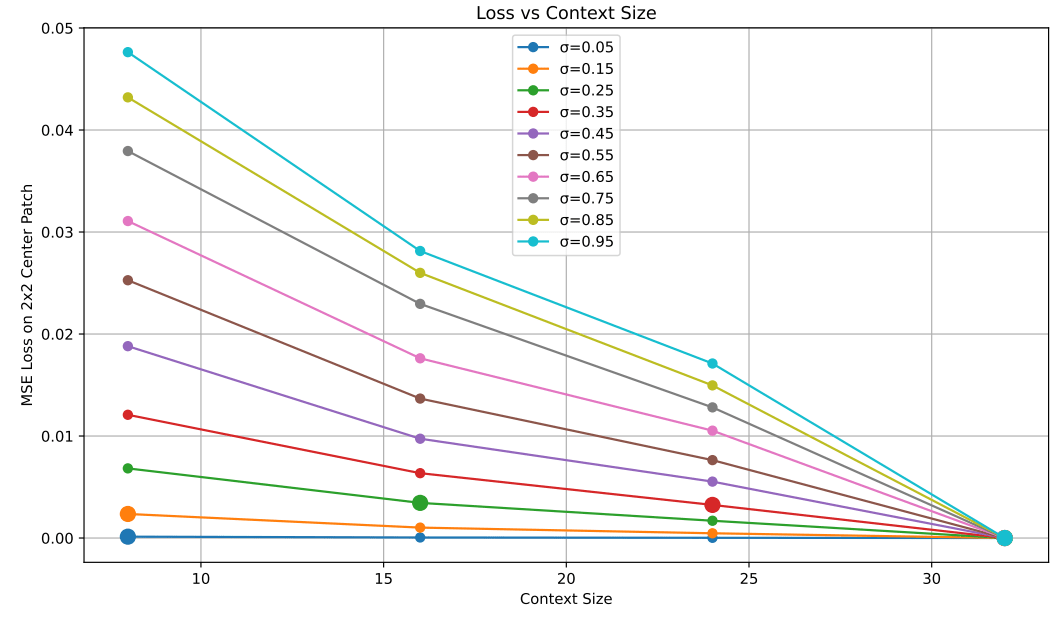
Denoising Loss vs Ambient Loss
Receptive Field
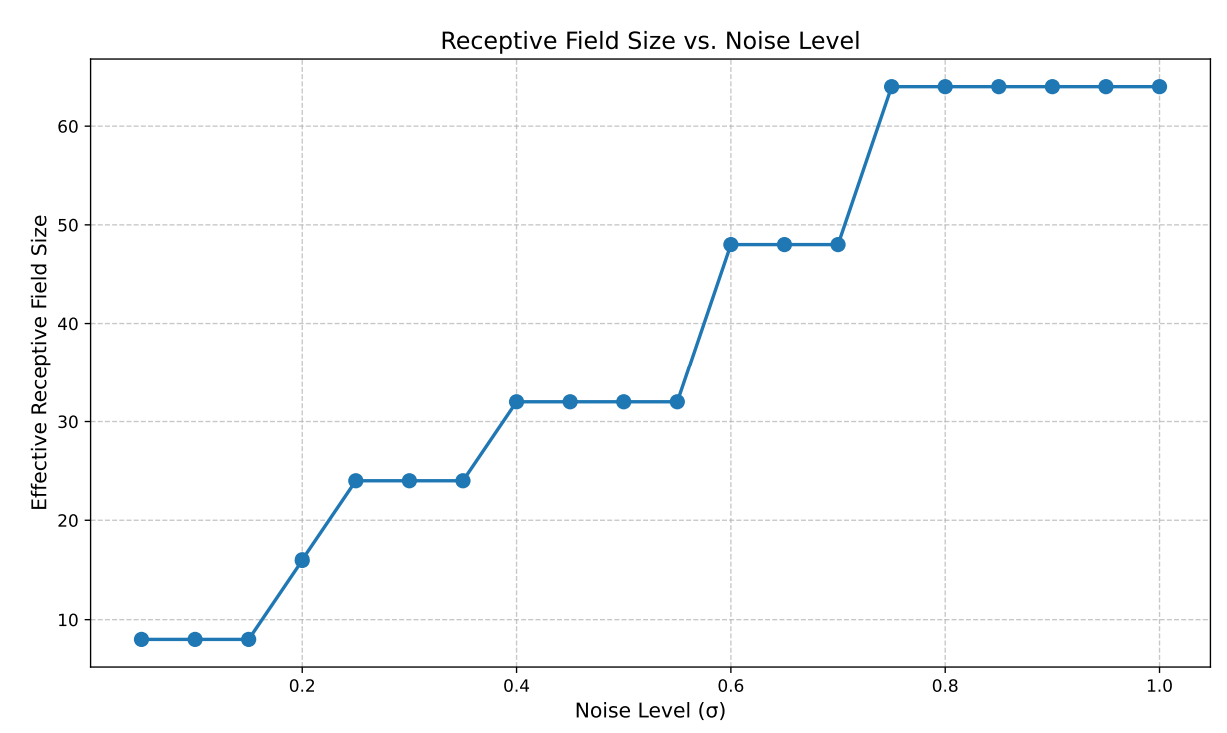
Denoising Loss vs Ambient Loss
Locality Experiments
Ambient Diffusion Omni: "use OOD with local similarity at low noise levels"
Intuition: If the receptive field at \(\sigma_{max}\) is sufficiently small that you cannot distinguish cats from dogs, then you can use cats to train a generator for dogs
Denoising Loss vs Ambient Loss
Ambient Diffusion Omni
Repeat:
- Sample (O, A, \(\sigma_{min}\), \(\sigma_{max}\)) ~ \(\mathcal{D}\)
- Choose noise level \(\sigma \in \{\sigma \in [0,1] : \sigma \geq \sigma_{min} \mathrm{\ or\ } \sigma \leq \sigma_{max}\}\)
- Optimize loss
\(\sigma=0\)
\(\sigma_{max}\)
Corrupt Data (\(\sigma\geq\sigma_{min}\))
Clean Data
Corrupt Data (\(\sigma\leq\sigma_{max}\))
\(\sigma_{min}\)
Denoising Loss vs Ambient Loss
Connection to Robotics
Locality in robotics:
- Smoothness
- Constraint satisfaction
- "Motion-level correctness"
Experiment:
(equivalent to cats vs dogs experiment in ambient diffusion omni)
- Clean data: sorts objects into bins
- Corrupt dataset 1: places objects into any bin
- Corrupt dataset 2: Open-X pick-and-place data