Amazon CoRo June Update

Jun 19, 2025

Adam Wei

Agenda

  1. IROS Paper Updates
  2. Cotraining plateau experiments
  3. MMD experiments
  4. Ambient Diffusion direction

IROS Updates: Accepted!

  • Submission was accepted to IROS
  • New website & code
  • New expermients

https://sim-and-real-cotraining.github.io/

Cotraining Plateau Experiments

Recall: Scaling up sim data improves performance up until a plateau...

Question: How much more real data would you need to collect to match the cotraining plateau?

Cotraining Plateau Experiments

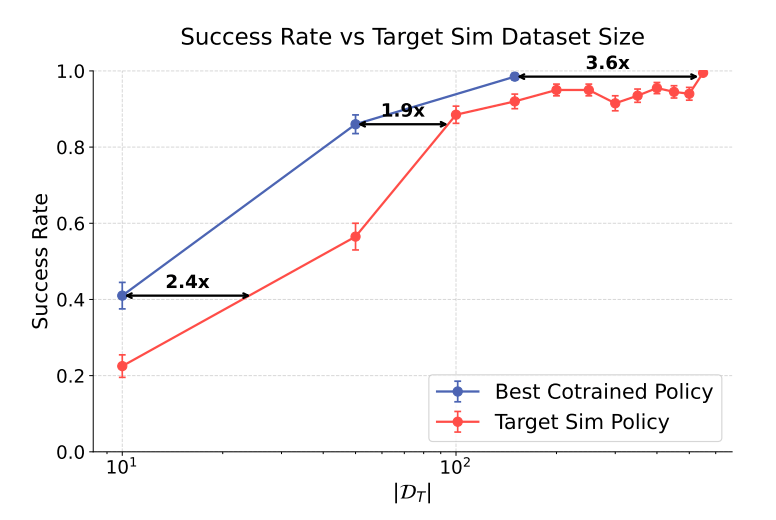
cotraining plateau \(\approx\) 2-3x more deal data

MMD Experiments

  • High-performing policies can discern sim from real
  • Overall, smaller sim2real gaps \(\implies\) better performance 

Recall that:

Questions:

1. Can/should we align the sim and real representations?

2. Can we improve performance by reducing the sim2real gap at the representation level?

MMD Experiments

\mathcal{L}_{\mathcal{D}^{\alpha}} = \alpha \mathcal{L}_{\mathcal D_R} + (1 - \alpha) \mathcal{L}_{\mathcal D_S}
\min_\theta \mathcal L_{\mathcal D^\alpha}(\theta) + \lambda\cdot\mathrm{dist}(p^S_\theta, p^R_\theta)

Denoising objective

Encourage aligned representations

  • Term 2 encourages the policy to ignore artifacts from sim2real (lighting, shadows, etc)
  • Term 1 encourages the policy to retain differences that are important for action prediction
  • Competing objectives are balanced by \(\lambda\)

MMD Experiments

\min_\theta \mathcal L_{\mathcal D^\alpha}(\theta) + \lambda\cdot\mathrm{dist}(p^S_\theta, p^R_\theta)

Denoising objective

Encourage aligned representations

\begin{aligned} \mathrm{Adversarial:\ }&\mathrm{dist}(p^S_\theta, p^R_\theta) = \max_\phi- \mathcal{L}_\mathrm{BCE}(\phi, \theta)\\ \mathrm{MMD:\ }& \mathrm{dist}(p^S_\theta, p^R_\theta) = \mathrm{MMD}(p^S_\theta, p^R_\theta) \end{aligned}

MMD Formulation

\min_\theta \mathcal L_{\mathcal D^\alpha}(\theta) + \lambda\cdot\max_\phi- \mathcal{L}_\mathrm{BCE}(\phi, \theta)\\

Goal: Learn a representation for sim and real that cannot be discerned by a classifier \(d_\phi\)

Issues: Adversarial training is unstable and challenging...

MMD Formulation

\min_\theta \mathcal L_{\mathcal D^\alpha}(\theta) + \lambda\cdot\mathrm{MMD}(p^S_\theta, p^R_\theta)
\mathrm{\hat{MMD}}(p^S_\theta, p^R_\theta) = \frac{1}{n^2}\sum_{i=1}^n \sum_{j=1}^n k(x_i, x_j) - \frac{2}{nm}\sum_{i=1}^n \sum_{j=1}^m k(x_i, y_j) \\ + \frac{1}{m^2}\sum_{i=1}^m \sum_{j=1}^m k(y_i, y_j)

Given samples \(x_i \sim p^S_\theta\) and \(y_i \sim p^R_\theta\):

Ex: \(k(x, y)=e^{-\frac{\lVert x-y\rVert_2^2}{\sigma^2}}\)

MMD Formulation

\min_\theta \mathcal L_{\mathcal D^\alpha}(\theta) + \lambda\cdot\mathrm{MMD}(p^S_\theta, p^R_\theta)
  • MMD is a common distance metric
  • Stable to train and differentiable

Results

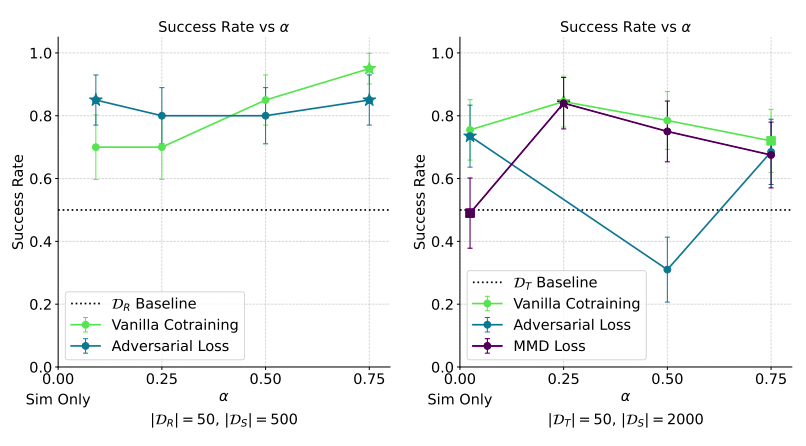
Adding an alignment objective does not improve performance and adds complexity

Ambient Diffusion

Learning from "clean" and "corrupt" data

Won't be going over the details of the algorithm...

... only the high-level ideas

High Frequency Corruption

\(t=0\)

\(t=T\)

\(t=t_n\)

\(\mathbb E[\lVert h_\theta(x_t, t) - x_0 \rVert_2^2]\)

\(\mathbb E[\lVert \frac{\sigma_t^2 - \sigma_{t_n}^2}{\sigma_t^2} h_\theta(x_t,t) + \frac{\sigma_{t_n}^2}{\sigma_t^2}x_t - x_{t_n} \rVert_2^2]\)

Use clean data to learn denoisers for \(t\in(0,T]\)

Use corrupt data to learn denoisers for \(t\in(t_n,T]\)

Initial Results

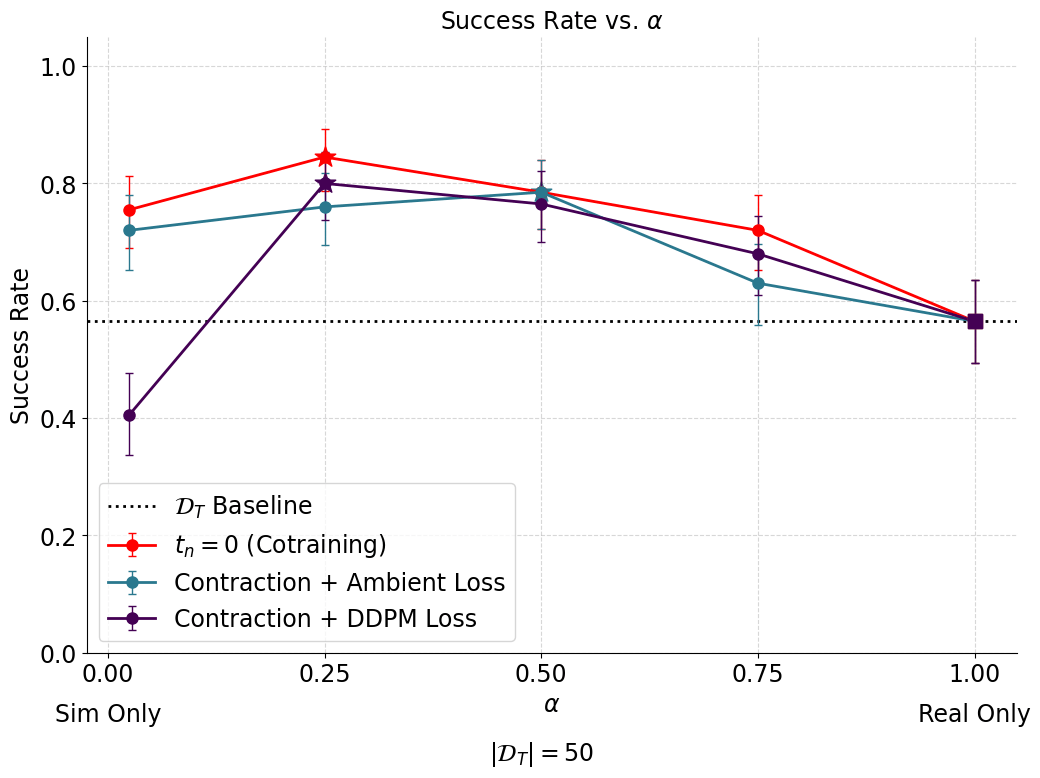
Current results are worse than mixing the data

  • Initial implementation was missing many key details
  • Baseline is very well-tuned
  • Sim-and-real cotraining may not be the right application?

Implementation Details

  • Sampler, noising once per data point, loss function scaling, classifier training process, etc...

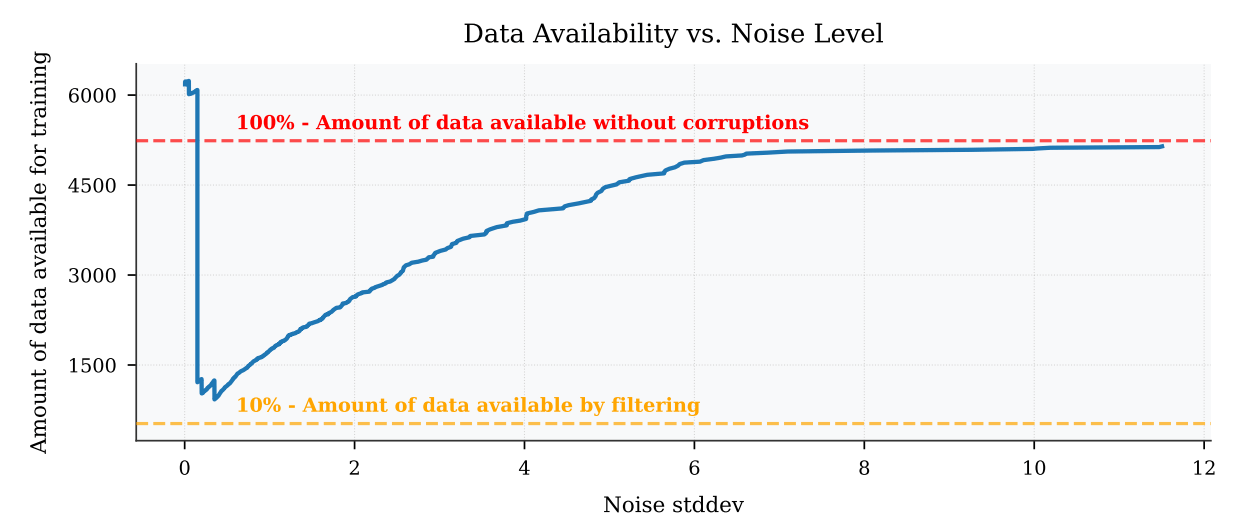
Low Frequency Corruptions

Intuition:

  • At low noise levels, only a small "patch" of the image is needed to diffuse optimally
  • Can use OOD samples at low noise levels so long as the local patches match the patches for the clean data

Future Directions

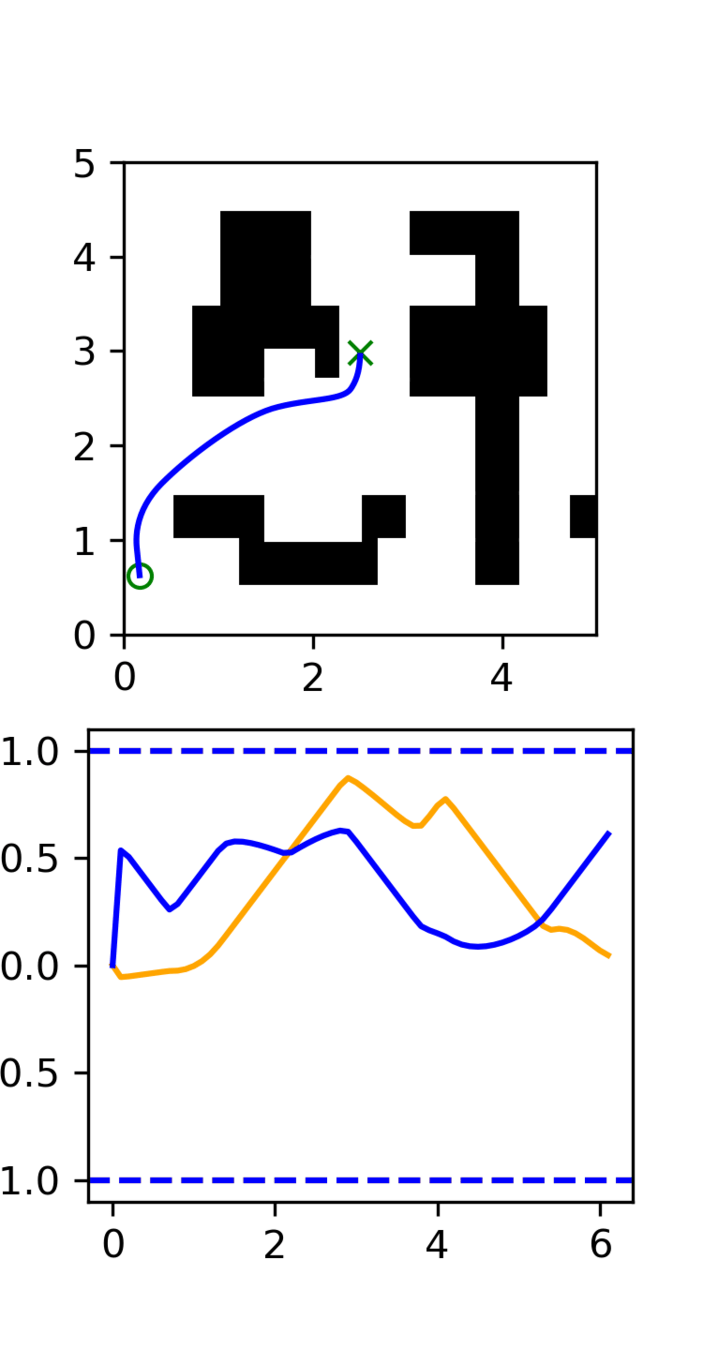
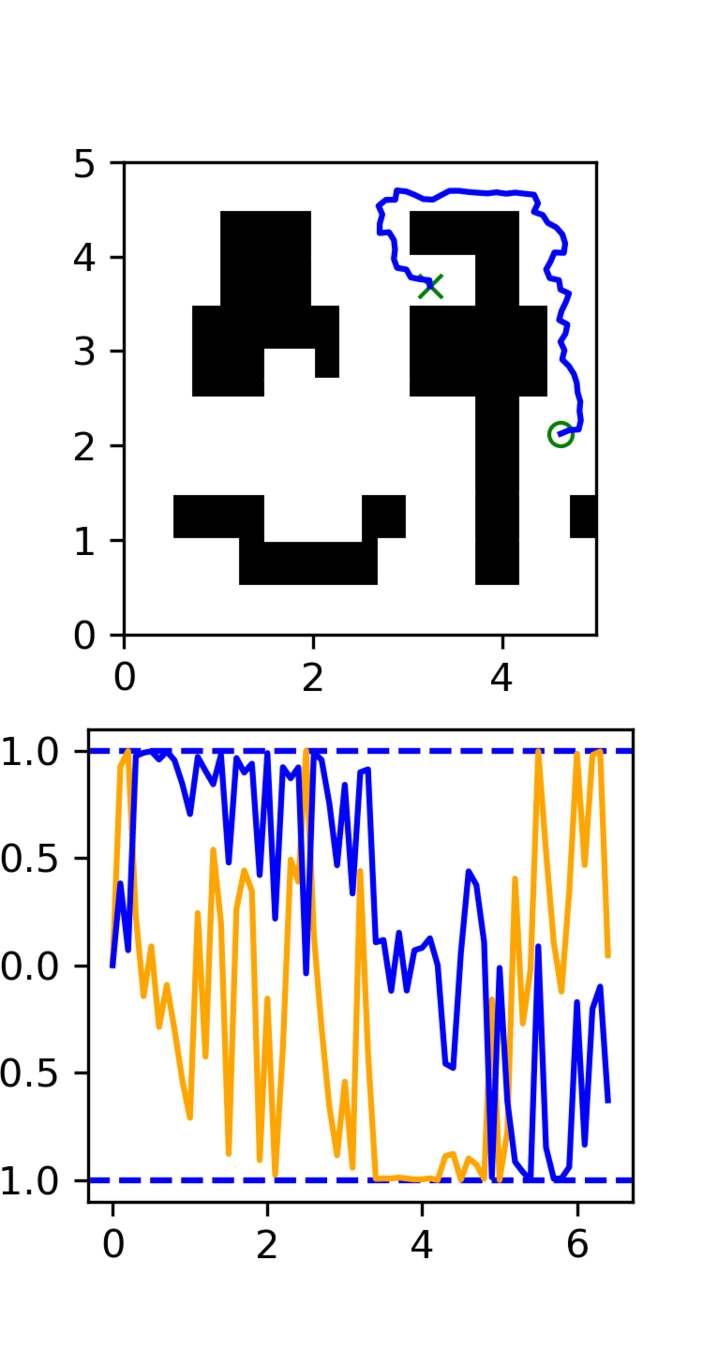
GCS

(clean)

RRT

(clean)

Task: Cotrain on GCS and RRT data

Goal: Sample clean and smooth GCS plans

  • Example of high frequency corruption
  • Common in robotics
  • Can be extended to 7DoF robot arm experiment