Learning From Out-of-Distribution Data in Robotics
Sept 24, 2025
Adam Wei


The Ingredients of Generative Modelling
Learning Algorithm
Data
Training Objective
Hypothesis Class
hyperparameters, etc ...

Model
The Ingredients of Generative Modelling
Learning Algorithm

Hypothesis Class
Data
hyperparameters, etc ...
Model
Training Objective
How can we train generative models when our data may be low quality or out-of-distribution (OOD)?
What can go wrong in [CV] data?
CC12M: 12M+ image + text captions


"Corrupt" Data:
Low quality images
"Clean" Data:
High quality images
Not just in CV: also in language, audio, robotics!

Distribution Shifts in Robot Data
- Sim2real gaps
- Noisy/low-quality teleop
- Task-level mismatch
- Changes in low-level controller
- Embodiment gap
- Camera models, poses, etc
- Different environment, objects, etc
robot teleop
simulation

Open-X

Training on OOD Data
robot teleop
simulation


Open-X

There is still value and utility in this data!
... we just aren't using it correctlty
Goal: to develop principled algorithms that change the way we use low-quality or OOD data
Ambient Diffusion

Giannis Daras

Diffusion


\(\sim p_0\)
\(\sim q_0\)
\(\sigma=0\)
Clean Data
Corrupt Data
\(\sigma=1\)
Ambient Diffusion


\(\sim p_0\)
\(\sim q_0\)
\(\sigma=0\)
Clean Data
Corrupt Data (\(\sigma > \sigma_{min}\))
\(\sigma_{min}\)
\(\sigma=1\)
Intuition: \(p_\sigma\) and \(q_\sigma\) Contract




\(p_0\)
\(q_0\)



\(\sigma=1\)
\(\sigma_{min}\)
\(\sigma=0\)
\(\mathrm{d}(p_\sigma, q_\sigma) \approx 0 < \epsilon\) for \(\sigma > \sigma_{min}\)
\(\implies\) can train with low-quality/OOD data at high noise levels
\(\sigma_{min}\) determines the utility of every data point
How to choose \(\sigma_{min}\)?
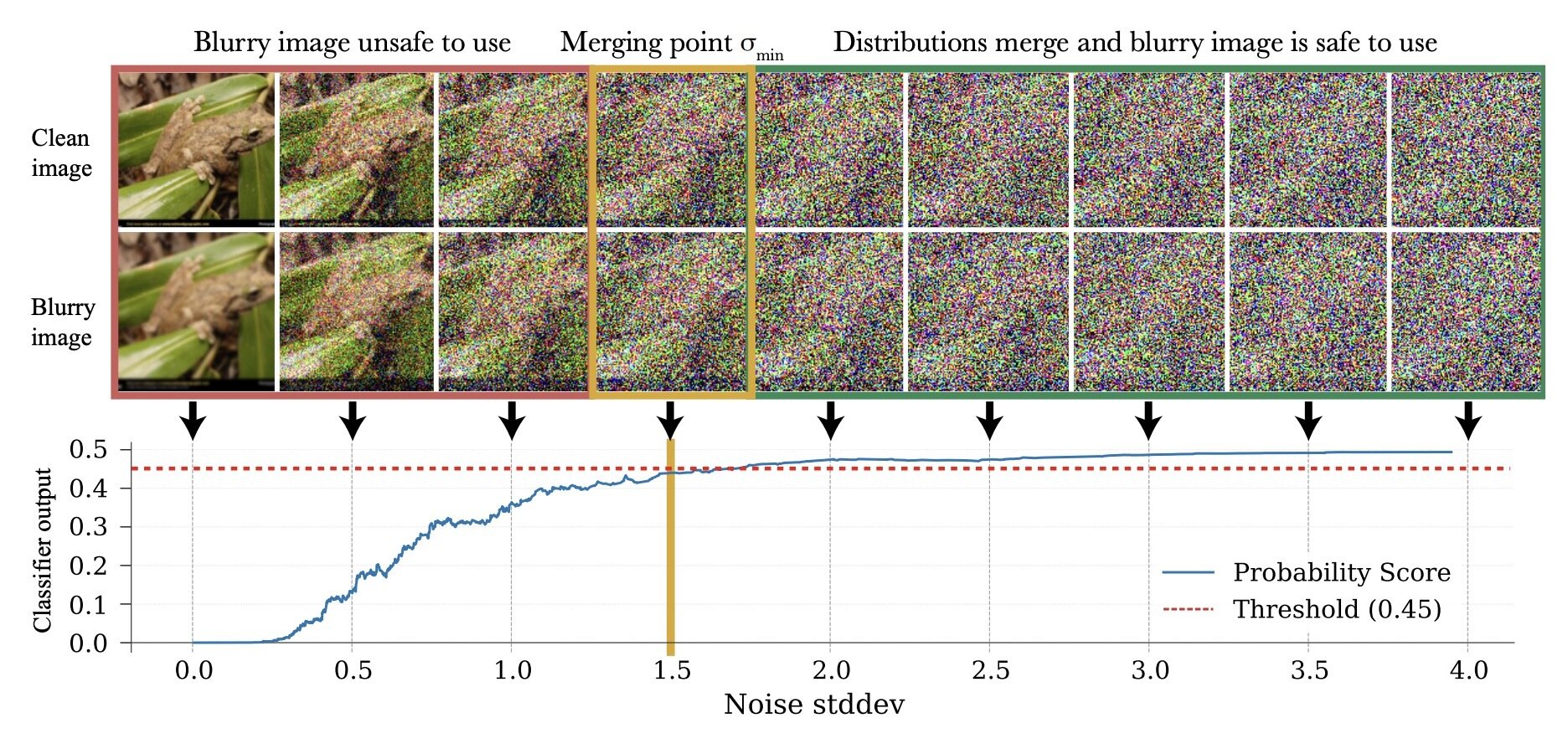
\(\sigma_{min}^i = \inf\{\sigma\in[0,1]: c_\theta (x_\sigma, \sigma) > 0.5-\epsilon\}\)
\(\implies \sigma_{min}^i = \inf\{\sigma\in[0,1]: d_\mathrm{TV}(p_\sigma, q_\sigma) < \epsilon\}\)*
* assuming \(c_\theta\) is perfectly trained
Loss Function
Loss Function (for \(x_0\sim q_0\))
\(\mathbb E[\lVert h_\theta(x_\sigma, \sigma) + \frac{\sigma_{min}^2\sqrt{1-\sigma^2}}{\sigma^2-\sigma_{min}^2}x_{\sigma} - \frac{\sigma^2\sqrt{1-\sigma_{min}^2}}{\sigma^2-\sigma_{min}^2} x_{\sigma_{min}} \rVert_2^2]\)
Ambient Loss
Denoising Loss
\(x_0\)-prediction
\(\epsilon\)-prediction
(assumes access to \(x_0\))
(assumes access to \(x_{\sigma_{min}}\))
\(\mathbb E[\lVert h_\theta(x_\sigma, \sigma) - x_0 \rVert_2^2]\)
\(\mathbb E[\lVert h_\theta(x_\sigma, \sigma) - \epsilon \rVert_2^2]\)
\(\mathbb E[\lVert h_\theta(x_\sigma, \sigma) - \frac{\sigma^2 (1-\sigma_{min}^2)}{(\sigma^2 - \sigma_{min}^2)\sqrt{1-\sigma^2}}x_t + \frac{\sigma \sqrt{1-\sigma^2}\sqrt{1-\sigma_{min}^2}}{\sigma^2 - \sigma_{min}^2}x_{\sigma_{min}}\rVert_2^2]\)
Derived using Tweedie's lemma:
\(\nabla \mathrm{log} p_{X_\sigma}(x_\sigma) = \frac{\mathbb E[X_0|X_\sigma=x_\sigma]-x_\sigma}{\sigma^2}\)
Loss Function
Loss Function (for \(x_0\sim q_0\))
Denoising Loss vs Ambient Loss
Ambient Diffusion
Repeat:
- Sample (O, A, \(\sigma_{min}\)) ~ \(\mathcal{D}\)*
- Choose noise level \(\sigma \in \{\sigma \in [0,1] : \sigma \geq \sigma_{min}\}\)
- Optimize denoising loss or ambient loss
\(\sigma=0\)
\(\sigma\geq\sigma_{min}\)
\(\sigma_{min}\)
*\(\sigma_{min} = 0\) for all clean samples
Loss Function
Loss Function (for \(x_0\sim q_0\))
Denoising Loss vs Ambient Loss
Ambient Diffusion Omni
\(\sigma=0\)
\(\sigma\geq\sigma_{min}\)
\(\sigma_{min}\)
*\(\sigma_{min} = 0\), \(\sigma_{max}=1\) for all clean samples
\(\sigma_{max}\)
\(\sigma\leq\sigma_{max}\)
Repeat:
- Sample (O, A, \(\sigma_{min}\), \(\sigma_{max}\)) ~ \(\mathcal{D}\)*
- Choose noise level \(\sigma \in \{\sigma \in [0,1] : \sigma \geq \sigma_{min} \ \mathrm{or} \ \sigma \leq \sigma_{max}\}\)
- Optimize denoising loss or ambient loss
Leverages locality structure in data...
Loss Function
Loss Function (for \(x_0\sim q_0\))
Denoising Loss vs Ambient Loss
2D Motion Planning Experiment
Distribution shift: Low-quality, noisy trajectories
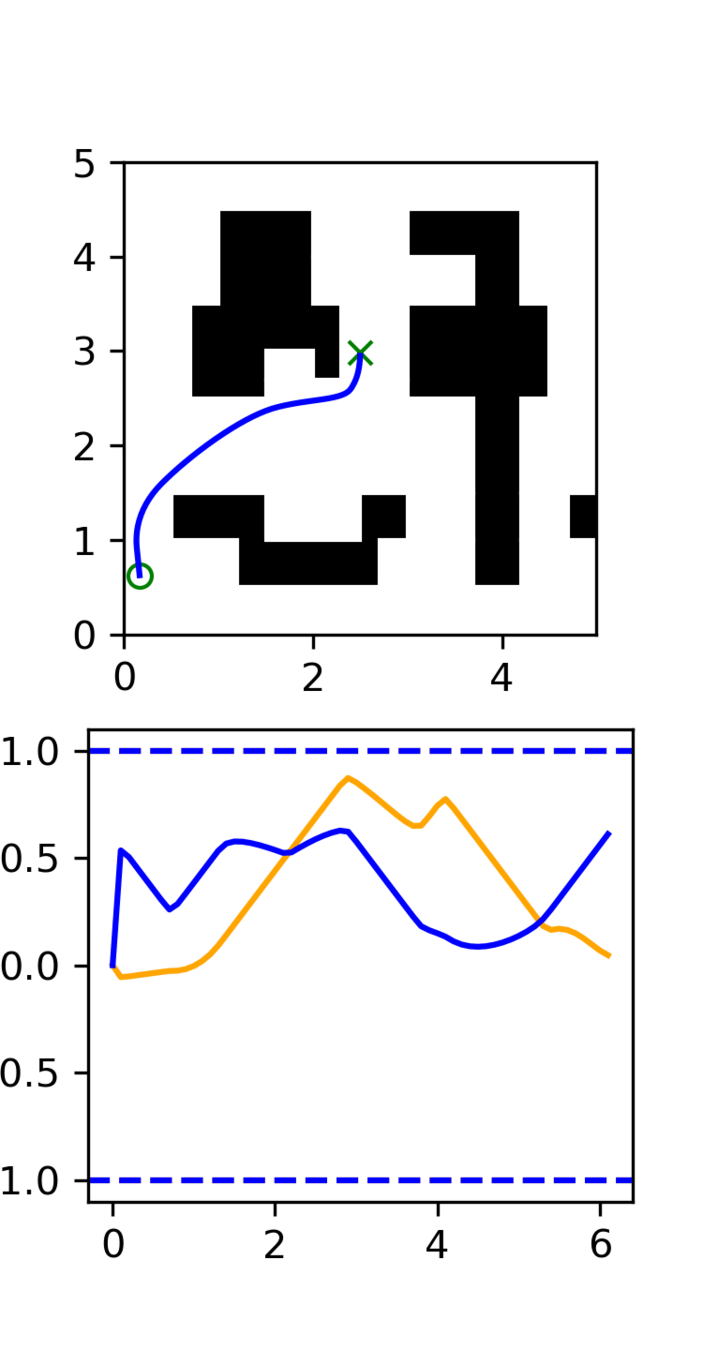
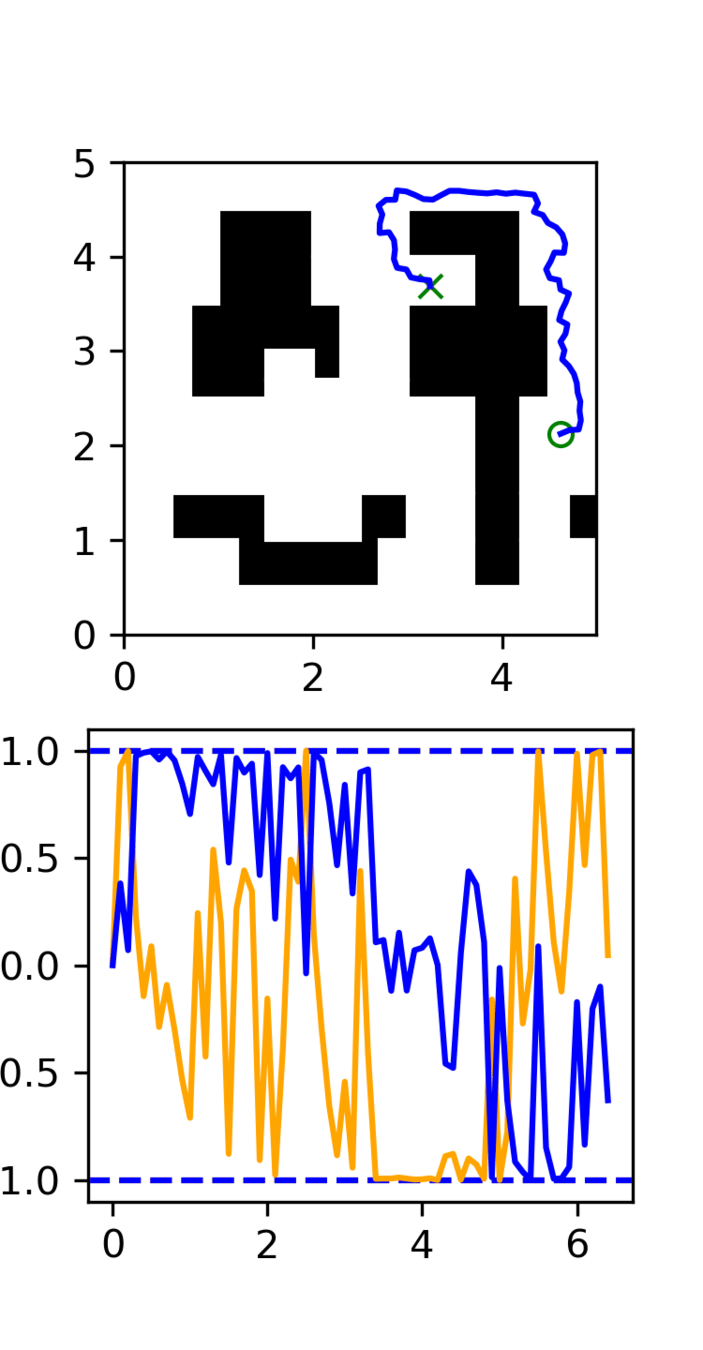
In-Distribution:
100 GCS trajectories
Out-of-Distribution:
5000 RRT trajectories
Loss Function
Loss Function (for \(x_0\sim q_0\))
Denoising Loss vs Ambient Loss
Results
Distribution shift: Low-quality, noisy trajectories
Diffusion
Ambient
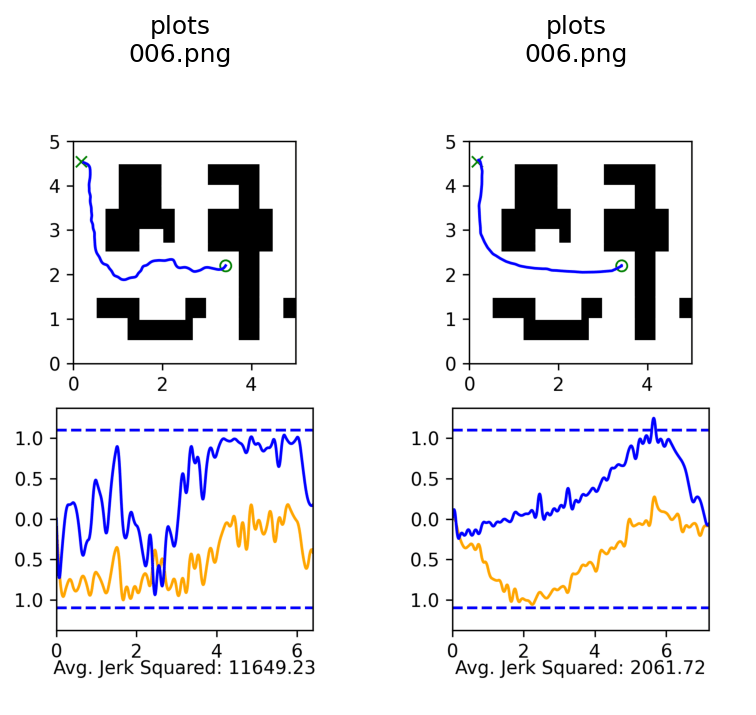

Success Rate: 98%
Average Jerk Squared: 5.5k
Success Rate: 91%
Average Jerk Squared: 14.5k
Loss Function
Loss Function (for \(x_0\sim q_0\))
Denoising Loss vs Ambient Loss
Sim-and-Real Cotraining
Distribution shift: sim2real gap
In-Distribution:
50 demos in "real" environment
Out-of-Distribution:
2000 demos in sim environment
Loss Function
Loss Function (for \(x_0\sim q_0\))
Denoising Loss vs Ambient Loss
Results
Distribution shift: sim2real gap
Diffusion*
Ambient
Diffusion w/ Reweighting*
75.5%
84.5%
93.5%
* From earlier work on sim-and-real cotraining
Loss Function
Loss Function (for \(x_0\sim q_0\))
Denoising Loss vs Ambient Loss
Bin Sorting
Distribution shift: task level mismatch, motion level correctness
In-Distribution:
50 demos with correct sorting logic
Out-of-Distribution:
200 demos with arbitrary sorting
2x
2x
Loss Function
Loss Function (for \(x_0\sim q_0\))
Denoising Loss vs Ambient Loss
Bin Sorting
Distribution shift: task level mismatch, motion level correctness
Diffusion
(50 correct demos)
Ambient
(50 correct, 200 OOD)
Cotrain
(50 correct, 200 OOD)
Score
(Correct logic)
Completion Rate
(Correct motions)
70.4%
48%
55.2%
88%
94.0%
88%
Loss Function
Loss Function (for \(x_0\sim q_0\))
Denoising Loss vs Ambient Loss
North Star Goal
North Star Goal: Train with internet scale data (Open-X, AgiBot, etc)
Plenty more experiments...
Happy to take questions or chat offline!