Privacy Attacks in Robotics

Nov 14, 2025

Adam Wei

Privacy in Robotics

Privacy Concerns (as the consumer...)

Data Protection

Data Misuse

Data Extraction

data!

Privacy Concerns

1. Are privacy attacks on robot models possible?

2. How can we defend against these attacks?

Easier direction

Harder direction

  • Proof by example
  • Empirics often insufficient
  • Need to clearly state assumptions for proofs, etc
  • People are clever ;)

Agenda

  1. Anatomy of a privacy attack
  2. Deep Leakage from Gradients
  3. Generative Model Inversion
  4. Robotics

Part 1

Anatomy of a Privacy Attack

Threat Model: Information Access

Black box: Access to

  • the model API

White box: Access to

  • model architecture
  • model parameters
  • previous checkpoints
  • training gradients

more access

\(\implies\)strong attacks

Threat Model: Information Access

Black box: Access to

  • the model API

White box: Access to

  • model architecture
  • model parameters
  • previous checkpoints
  • training gradients

more access

\(\implies\)strong attacks

Robotics?

Threat Model: Type of Attacks

Membership

Was the model trained on a specific datapoint?

Reconstruction

Can I reconstruct the training dataset?

Property

Given a partial datapoint, can I infer other properties?

Model Extraction

Can I extract the model parameters, etc?

Threat Model: Type of Attacks

Membership

Was the model trained on a specific datapoint?

Reconstruction

Can I reconstruct the training dataset?

Property

Given a partial datapoint, can I infer other properties?

Model Extraction

Can I extract the model parameters, etc?

Reconstruction Attacks

Black box: Access to

  • the model API

White box: Access to

  • model architecture
  • model parameters
  • previous checkpoints
  • training gradients

Deep Leakage from Gradients

Generative Model Inversion

Part 2

Deep Leakage from Gradients (DLG)

Federated Learning

Central Server

\(W_t\)

\(W_t\)

\(\nabla_{W_t} \mathcal{L}_{1}\)

\(\nabla_{W_t} \mathcal{L}_{2}\)

\(W_{t+1} = W_t -\frac{\eta}{N}\sum_i\nabla_{W_t} \mathcal L_i\)

Deep Leakage from Gradients

Goal: reconstruct datapoints that would produce the same gradient

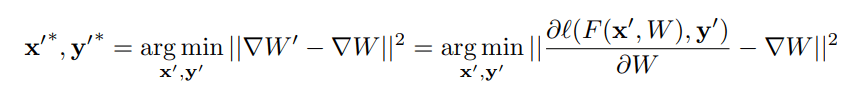
Deep Leakage from Gradients

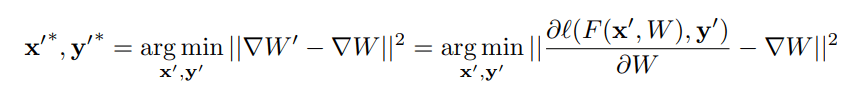
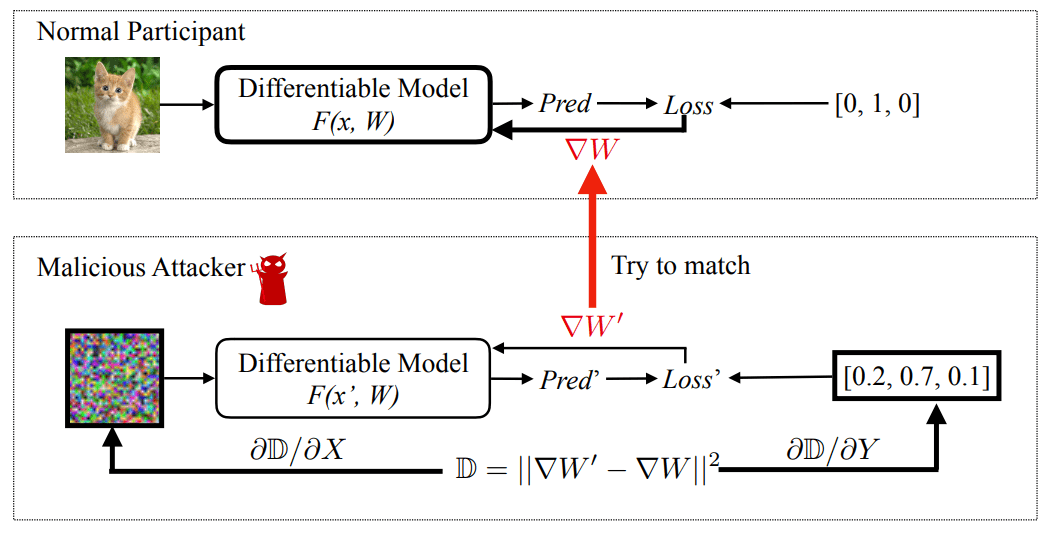
Deep Leakage from Gradients

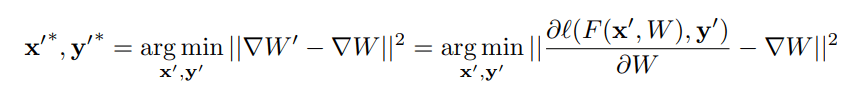
Algorithm: given \(W\), \(\nabla W\), \(f_W\):

Initialize \((x',y')\sim \mathcal N(0,I)\)

Repeat until convergence:

\((x', y') \leftarrow (x', y') - \eta \nabla_{(x', y')} D\)

Solve with L-BFGS

(avoids Hessian computation)

\(D = \lVert \nabla W' - \nabla W \rVert_2^2\)

\(\nabla W' = \nabla_W \mathcal L(f_W(x'), y')\)

Variations of DLG

iDLG: Exploit classification structure to find ground truth labels

Many other variants...

\begin{aligned} (x'^*, y'^*) = \argmin_{(x', y')} &\ \mathrm{dist}(\nabla W', \nabla W) + \mathrm{regularization}\\ s.t.& \quad\mathrm{constraints}\\ & \quad \mathrm{prior\ knowledge} \end{aligned}

ex. optimize \(z\) instead of \(x'\), where \(x' = G(z)\)

Results & Defense

Defense: Adding zero-mean noise to gradients

  • Gradients remain unbiased \(\implies\) still contribute to training, but much harder to reconstruct

Part 3

Generative Model Inversion

Assumptions

  1. Access to the weights of a model that maps inputs to labels
  2. Prior knowledge of the input distribution
  3. Known labels; the goal is to recover the inputs

Method

1. Train a WGAN (with some extra tricks...)

  • Discriminator (D): predicts probability that image is real
  • Generator (G): generates images from latents x

2. Let \(C(x)\) be the likelihood of the desired output given \(x\)

3. Solve

\hat z = \argmax_z D(G(z)) + \lambda \log(C(G(z)))

Realism

Likelihood of target output

4. \(\hat x = G(\hat z)\)

Results

Model Inversion Attacks

\begin{aligned} x^* = \argmax_{x} &\ \log p_f(y|x) + \lambda \log p_\mathrm{priori}(x)\\ \mathrm{s.t.}& \quad\mathrm{constraints}\\ & \quad \mathrm{prior\ knowledge} \end{aligned}
  • Solved with zeroth or first-order methods
  • Brittle!
  • Improves with generative modeling (ex. flows)

 

Part 4

Robotics & Generative Modeling

Attacks in Generative Modeling

Conditioning variables are known;

outputs are sensitive

Robotics

(subset) of conditioning variables are sensitive!

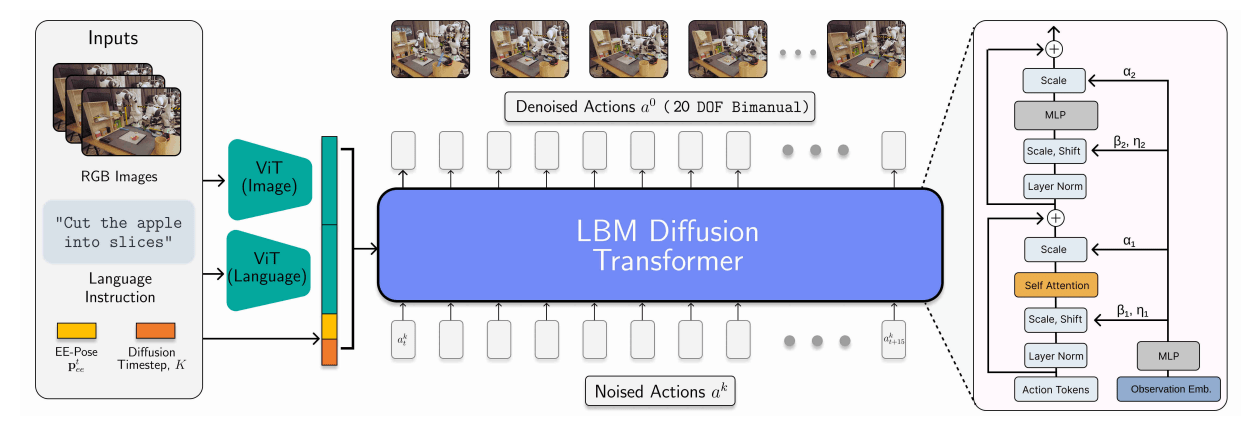
Outputs (may be) known;

Robotics

Approaches

  • Try existing attacks
  • Develop new attacks that leverage the structure in robotics

Thank You!

Thank You!