Unifying Perspectives on Diffusion

RLG Short Talk

May 3, 2024

Adam Wei

Interpretations of Diffusion

Goal: Show how the different interpretations of diffusion are connected.

Diffusion

Sohl-Dickstein et al

DDPM

Ho et al

SMLD

Song et al

SDE

Song et al

Projection

Permenter et al

2015

2019

2021

2023

Denoising

Score-based

Optimization

2020

What this presentation is not...

  • Not a deep dive into the papers
  • Not a rigorous mathematical presentation
  • Not about how to train diffusion policies or score-matching

Goal: Show how the different interpretations of diffusion are connected.

SDE Interpretation

Summary

\epsilon_\theta(x,t) \propto -\nabla_x \log p_t(x)

2. Score-based and denoiser approaches are discrete instantiations of the SDE approach

1. Both SMLD and DDPM learn the score function of the noisy distributions.

Interpretations of Diffusion Policy

Diffusion

Sohl-Dickstein et al

DDPM

Ho et al

SMLD

Song et al

SDE

Song et al

Projection

Permenter et al

2015

2019

2021

2023

Denoising

Score-based

Optimization

2020

Goal: Show how the different interpretations of diffusion are connected.

SMLD: Langevin Dynamics (1/6)

X_{t+h} = X_t + h\red{\nabla \log p(X_t)} + \sqrt{2h} \epsilon

Intuition: On each step..

Key Takeaway:                              ​     under regularity conditions

X_t \rightarrow X \sim p
  1. Move in a direction that increases log probability
  2. Add Gaussian noise (prevent collapse onto local maxima of p)

"Score Function"

Goal: Sample from some distribution p

SMLD: Langevin Dynamics (2/6)

"Gradient ascent with Gaussian noise"

https://www.peterholderrieth.com/blog/2023/Langevin-Dynamics-An-introduction-for-Machine-Learning-Engineers/

SMLD: Issues with Langevin Dyanmics (3/6)

Manifold Hypothesis: real world data lies along low-dimensional manifolds in high dimensional spaces.

Practical Implications

  1. \(\nabla\log p(X)\approx 0\) in most of the ambient space \(\implies\) Langevin dynamics converges slowly
  2. No samples \(X\sim p\) in most of ambient space \(\implies\) hard to accurately learn \(\nabla\log p(X) \  \forall X\)

 

Solution: noising! (increase support of p)

SMLD: Algorithm (4/6)

1. Construct sequence of noised distributions:

q_{\sigma_1},\ ... \ ,q_{\sigma_L}
\begin{aligned} &q_{\sigma_1} \approx p_{data} \\ &q_{\sigma_L} \approx \text{Gaussian} \end{aligned}

2. Learn scores for noised distributions \(q_{\sigma_i}\) :

s_\theta(X, \sigma_i) \approx \nabla \log q_{\sigma_i}(X) \ \forall i \in [L]

3. Sample from annealed Langevin Dynamics 

X_{i-1} = X_i + h\red{s_\theta(X_i,\sigma_i)} + \sqrt{2h} \epsilon

SMLD: Algorithm (5/6)

X_{i-1} = X_i + h\red{s_\theta(X_i,\sigma_i)} + \sqrt{2h} \epsilon
X_{t+s} = X_t + h\red{\nabla \log p(X_t)} + \sqrt{2h} \epsilon

Advantages

  1. Faster convergence
  2. Better learned scores
\approx \nabla \log q_{\sigma_i}(X)

replace \(\nabla \log p(X)\) with "noisy scores"

SMLD: Results (6/6)

SMLD: Connection to control... (Bonus)

1. Design a trajectory in distribution space

q_{\sigma_1},\ ... \ ,q_{\sigma_L}

2. Use Langevin Dynamics to track this trajectory

X_{i-1} = X_i + h\red{s_\theta(X_i,\sigma_i)} + \sqrt{2h} \epsilon

TODO: DRAW IMAGE

Interpretations of Diffusion Policy

Diffusion

Sohl-Dickstein et al

DDPM

Ho et al

SMLD

Song et al

SDE

Song et al

Projection

Permenter et al

2015

2019

2021

2023

Denoising

Score-based

Optimization

2020

Goal: Show how the different interpretations of diffusion are connected.

DDPM: Overview (1/6)

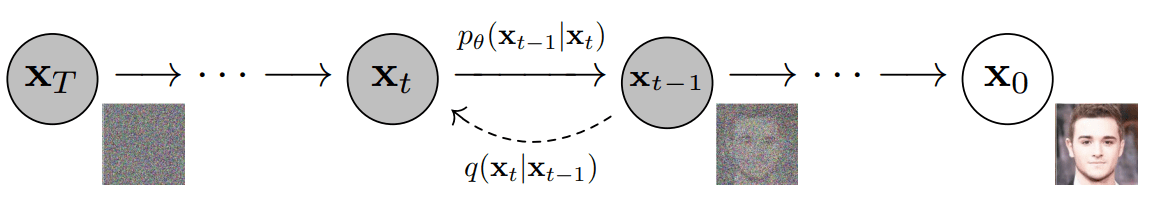
Forward Process: Noise the data

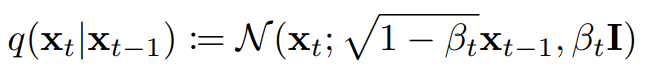
Backward Process: Denoising

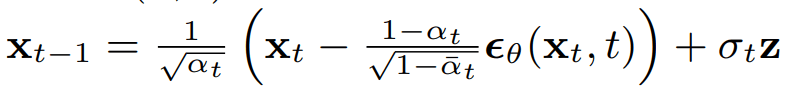
DDPM: Results (2/6)

DDPM vs SMLD (3/6)

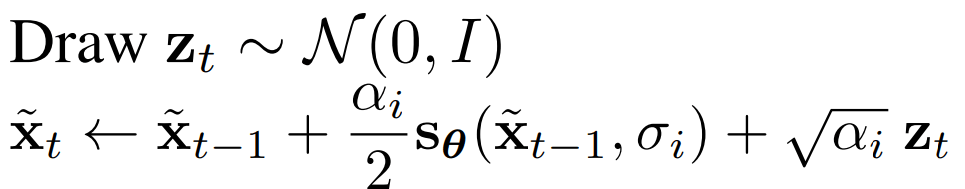
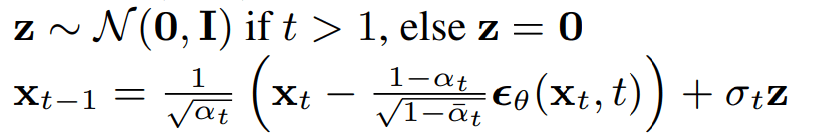
SMLD Sampling:

DDPM Sampling:

Screenshots from the papers. Notation is not same!!

DDPM vs SMLD (4/6)

SMLD Loss

DDPM Loss

Screenshots of original loss functions. Notation is not same!!

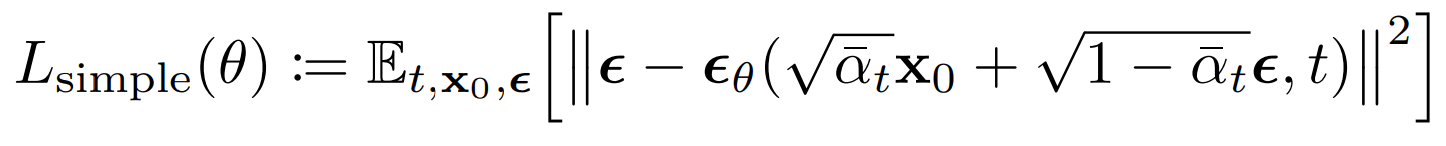
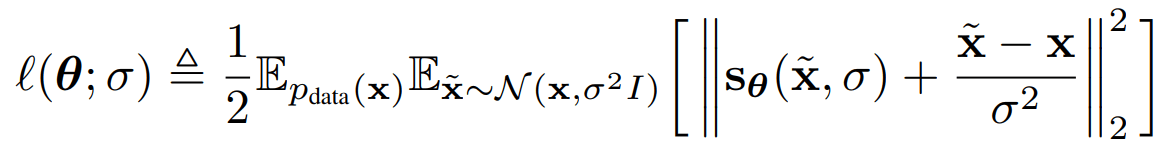
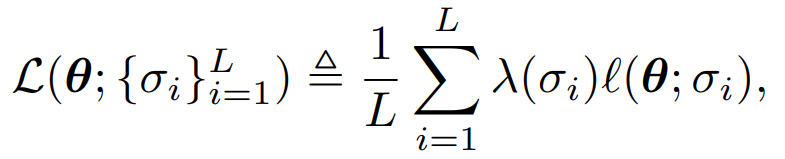
DDPM vs SMLD (5/6)

SMLD Loss*:

DDPM Loss*:

\mathbb{E}_{\blue{t,x_0,\epsilon}}[\lambda(t)\lVert \red{\epsilon_\theta(\sqrt{\bar{\alpha_t}}x_0 + \sigma_t\epsilon,\ t)} - \green{\epsilon} \rVert_2^2]

*Rewritten loss functions with severe abuse of notation to highlight similarities.

\mathbb{E}_{\blue{t,x_0,\epsilon}} [\lambda(\sigma_t)\lVert \red{s_\theta(x_0 + \sigma_t\epsilon,\ \sigma_t)} + \green{\frac{\epsilon}{\sigma_t}} \rVert_2^2]
x_t
x_t

DDPM: Connection to Score-Matching (6/6)

Key Takeaway

\nabla \log p_t(x_t) = -\frac{1}{\sqrt{1-\bar{\alpha_t}}}\epsilon_0 = -\frac{1}{\sqrt{\mathbb{V}[X_t | X_0]}}\epsilon_0
\implies \epsilon_\theta(x,t) \approx -\sqrt{\mathbb{V}[X_t | X_0]}\red{\nabla \log p_t(x)}

Proofs (via Tweedies, etc)

[1] Understanding Diffusion Models: A Unified Perspective

[2] Peter Holderrieth's Blog

SDE Interpretation

Interpretations of Diffusion Policy

Diffusion

Sohl-Dickstein et al

DDPM

Ho et al

SMLD

Song et al

SDE

Song et al

Projection

Permenter et al

2015

2019

2021

2023

Denoising

Score-based

Optimization

2020

Goal: Show how the different interpretations of diffusion are connected.

SDE Interpretation

SDE: Overview (1/8)

SMLD/DDPM: Noise and denoise in discrete steps.

 

SDE: Noise and denoise according to continuous SDEs

SDE Interpretation

SDE: Overview (2/8)

Key Takeaway: SMLD and DDPM are discrete instances of the SDE interpretation!

SDE Interpretation

SDE: Ito-SDE (3/8)

dX =f(X,t)dt+g(t)dW

[1] Bernt Øksendal, 2003 [2] Brian D O Anderson, 1982

1. If f and g are Lipschitz, the Ito-SDE has a unique solution [1].

2. The reverse-time SDE is [2]:

dX = [f(X,t)-g^2(t)\red{\nabla_x\log p_t(X)}]dt + g(t)d\bar{W}
\begin{aligned} &X(\cdot) \text{ is a stochastic process }\\ &X(t) \text{ is a random variable} \\ \end{aligned}

"Ito-SDE"

SDE Interpretation

SDE: Algorithm (4/8)

1. Define f and g s.t. X(0) ~ p transforms into a tractable distribution, X(T)

dX =f(X,t)dt+g(t)dW

2. Learn

s_\theta(x, t) \approx \nabla_x \log p_{X_t}(x)

3. To sample:

 - Draw sample x(T)

 - Reverse the SDE until t=0

SMLD/DDPM

dX = [f(X,t)-g^2(t)\red{s_\theta(X,t)}]dt + g(t)d\bar{W}

SDE Interpretation

SDE: SMLD (5/8)

x_i = x_{i-1} + \sqrt{\sigma_i^2 - \sigma_{i-1}^2}z_{i-1}

Forward (N-steps):

x(t+ \Delta t) = x(t) + \sqrt{\sigma^2(t + \Delta t) - \sigma^2(t)}z(t)

SMLD as an Ito SDE...

SDE Interpretation

SDE: SMLD (6/8)

x(t+ \Delta t) = x(t) + \sqrt{\sigma^2(t + \Delta t) - \sigma^2(t)}z(t)
\begin{aligned} &N \rightarrow \infty \\ &\Delta t = \frac{T}{N}\rightarrow 0 \end{aligned}
dX = \sqrt{\frac{d[\sigma^2(t)]}{dt}}dW
\implies
\begin{aligned} &f(x,t) = 0 \\ &g(t) = \sqrt{\frac{d[\sigma^2(t)]}{dt}} \end{aligned}

SDE Interpretation

SDE: DDPM (7/8)

x_i = \sqrt{1-\beta_i}x_{i-1} + \sqrt{\beta_i}z_{i-1}

Forward (N-steps):

x(t+ \Delta t) = \sqrt{1-\beta(t+\Delta t)\Delta t}x(t) + \sqrt{\beta(t+\Delta t)\Delta t}z(t)
\begin{aligned} &N \rightarrow \infty \\ &\Delta t = \frac{T}{N}\rightarrow 0 \\ \end{aligned}
dX = -\frac{1}{2}\beta(t)Xdt + \sqrt{\beta(t)}dW
\implies
\begin{aligned} &f(x,t) = -\frac{1}{2}\beta(t)x \\ &g(t) = \sqrt{\beta(t)} \end{aligned}

Similarly for DDPM...

SDE Interpretation

SDE: Summary (8/8)

\begin{aligned} &f(x,t) = 0 \\ &g(t) = \sqrt{\frac{d[\sigma^2(t)]}{dt}} \end{aligned}
dX =f(X,t)dt+g(t)dW
dX = [f(X,t)-g^2(t)\red{\nabla_x\log p_t(X)}]dt + g(t)d\bar{W}

SDE Interpretation:

Forward:

Reverse:

\begin{aligned} &f(x,t) = -\frac{1}{2}\beta(t)x \\ &g(t) = \sqrt{\beta(t)} \end{aligned}

SMLD

DDPM

SDE Interpretation

Summary

\epsilon_\theta(x,t) \propto -\nabla_x \log p_t(x)

2. Score-based and denoiser approaches are discrete instantiations of the SDE approach

1. Both SMLD and DDPM learn the score function of the noisy distributions.

SDE Interpretation

Resources

Papers: Sohl-Dickstein, SMLD, DDPM, SDE, Permenter, Understanding Diffusion Models

Blogs: Lillian Weng, Yang Song, Peter E. Holderrieth

Tutorials: Yang Song, "What are Diffusion Models"

Diffusion in Robotics: https://github.com/mbreuss/diffusion-literature-for-robotics

Thank you!