Learning From Corrupt/Noisy Data

RLG Long Talk

May 2, 2025

Adam Wei

Agenda

  1. Motivation
  2. Ambient Diffusion
  3. Interpretation
  4. Experiments

... works in progress

Part 1

Motivation

Sources of Robot Data

Open-X

 expert robot teleop

 robot teleop

simulation

Goal: sample "high-quality" trajectories for your task

Train on entire spectrum to learn "high-level" reasoning, semantics, etc

"corrupt"

"clean"

Corrupt Data

Corrupt Data

Clean Data

Computer Vision

Language

Poor writing, profanity, toxcity, grammar/spelling errors, etc

👀

Research Questions

  1. How can we learn from both clean and corrupt data?
  2. Can these algorithms be adapted for robotics?

Giannis Daras

Part 2a

Ambient Diffusion

Diffusion: Sample vs Epsilon Prediction

\mathbb E[\lVert h_\theta(x_t, t) - x_0 \rVert_2^2]
\mathbb E[\lVert \epsilon_\theta(x_t, t) - \epsilon \rVert_2^2]

Epsilon prediction:

Sample prediction:

affine transform

h^*(x_t, t) = \mathbb E_{p_{X_0|X_t=x_t}}[X_0 | X_t = x_t]

Diffusion: VP vs VE

X_t = \sqrt{1-\sigma_t^2}X_0 + \sigma_t Z

Variance preserving:

Variance exploding:

X_t = X_0 + \sigma_t Z

Variance exploding and sample-prediction simplify analysis

... analysis can be extended to DDPM

Ambient Diffusion

Assumptions

1. Each corrupt data point contains additive gaussian noise up to some noise level \(t_n\)

X_{t_n} = X_0 + \sigma_{t_n} Z
X_0\sim p_0,\ Z\sim \mathcal N(0, I)

\(t=0\)

\(t=T\)

\(t=t_n\)

Corrupt data: \(X_{t_n} = X_0 + \sigma_{t_n} Z\)

Ambient Diffusion

Assumptions

1. Each corrupt data point contains additive gaussian noise up to some noise level \(t_n\)

2. \(t_n\) is known for each dataset or datapoint

\(t=0\)

\(t=T\)

\(t=t_n\)

Corrupt data: \(X_{t_n} = X_0 + \sigma_{t_n} Z\)

Naive Diffusion

\(t=0\)

\(t=T\)

\(t=t_n\)

noise

denoise

\mathbb E[\lVert h_\theta(x_t, t) - x_{t_n} \rVert_2^2]
\implies h_\theta^*(x_t, t) = \mathbb E[X_{t_n} | X_t = x_t]
x_t = x_{t_n} + \sqrt{\sigma_t^2 - \sigma_{t_n}^2}Z

Forward Process

Backward Process

\implies h_\theta^*(x_t, t) = \mathbb E[X_{t_n} | X_t = x_t]

Can we do better?

\(t=0\)

\(t=T\)

\(t=t_n\)

noise

denoise

h_\theta^*(x_t, t) = \mathbb E[X_0 | X_t = x_t]
x_t = x_{t_n} + \sqrt{\sigma_t^2 - \sigma_{t_n}^2}Z

Forward Process

Backward Process

Can we do better?

\(t=0\)

\(t=T\)

\(t=t_n\)

noise

denoise

How can we learn \(h_\theta^*(x_t, t) = \mathbb E[X_0 | X_t = x_t]\) using noisy samples \(X_{t_n}\)?

Ambient Diffusion

\mathbb E[\lVert \frac{\sigma_t^2 - \sigma_{t_n}^2}{\sigma_t^2} h_\theta(x_t,t) + \frac{\sigma_{t_n}^2}{\sigma_t^2}x_t - x_{t_n} \rVert_2^2]
\implies h_\theta^*(x_t, t) = \mathbb E[X_0 | X_t = x_t]

Ambient Loss

Note that this loss does not require access to \(x_0\)

How can we learn \(h_\theta^*(x_t, t) = \mathbb E[X_0 | X_t = x_t]\) using noisy samples \(X_{t_n}\)?

\mathbb E[\lVert h_\theta(x_t,t) - x_0 \rVert_2^2]

Diffusion Loss

No access to \(x_0\)

Ambient Diffusion

We can learn \(\mathbb E[X_0 | X_t=x_t]\) using only corrupted data!

Remarks

  • From any given \(x_{t_n}\), you cannot recover \(x_0\)
  • Given \(p_{X_{t_n}}\), you can compute \(p_{X_0}\)
  • "No free lunch": learning \(p_{X_0}\) from \(X_{t_n}\) requires more samples than learning from clean data \(X_0\)
\mathbb E[\lVert \frac{\sigma_t^2 - \sigma_{t_n}^2}{\sigma_t^2} h_\theta(x_t,t) + \frac{\sigma_{t_n}^2}{\sigma_t^2}x_t - x_{t_n} \rVert_2^2]

Proof: "Double Tweedies"

\(X_{t} = X_0 + \sigma_{t}Z\)

\(X_{t} = X_{t_n} + \sqrt{\sigma_t^2 - \sigma_{t_n}^2}Z\)

\(\nabla \mathrm{log} p_t(x_t) = \frac{\mathbb E[X_0|X_t=x_t]-x_t}{\sigma_t^2}\)

\(\nabla \mathrm{log} p_t(x_t) = \frac{\mathbb E[X_{t_n}|X_t=x_t]-x_t}{\sigma_t^2-\sigma_{t_n}^2}\)

\mathbb E[X_0 | X_t=x_t] = \frac{\sigma_t^2}{\sigma_t^2 - \sigma_{t_n}^2}\mathbb E[X_{t_n} | X_t=x_t] - \frac{\sigma_{t_n}^2}{\sigma_t^2 - \sigma_{t_n}^2}x_t

(Tweedies)

(Tweedies)

Proof: "Double Tweedies"

\(g_\theta(x_t,t) := \frac{\sigma_t^2 - \sigma_{t_n}^2}{\sigma_t^2} h_\theta(x_t,t) + \frac{\sigma_{t_n}^2}{\sigma_t^2}x_t\).

\mathcal L = \mathbb E [\lVert \frac{\sigma_t^2 - \sigma_{t_n}^2}{\sigma_t^2} h_\theta(x_t,t) + \frac{\sigma_{t_n}^2}{\sigma_t^2}x_t - x_{t_n} \rVert_2^2]

Ambient loss:

\implies \mathcal L = \mathbb E [\lVert g_\theta(x_t, t) - x_{t_n} \rVert_2^2]
\implies g_{\theta}^*(x_t,t) = \mathbb E [X_{t_n} | X_t = x_t]

Proof: "Double Tweedies"

\implies g_{\theta}^*(x_t,t) = \mathbb E [X_{t_n} | X_t = x_t]

\(\frac{\sigma_t^2 - \sigma_{t_n}^2}{\sigma_t^2} h_\theta^*(x_t,t) + \frac{\sigma_{t_n}^2}{\sigma_t^2}x_t = \mathbb E [X_{t_n} | X_t = x_t]\)

\begin{aligned} h_\theta^*(x_t,t) &= \frac{\sigma_t^2}{\sigma_t^2 - \sigma_{t_n}^2}\mathbb E[X_{t_n} | X_t=x_t] - \frac{\sigma_{t_n}^2}{\sigma_t^2 - \sigma_{t_n}^2}x_t \\ &= \mathbb E[X_0 | X_t=x_t] \end{aligned}

(from double Tweedies)

\(\implies\)

\(\implies\)

(definition of \(g_\theta\))

Training Algorithm

For each data point:

Clean data: \(t\in (0, T]\)

\(x_t = x_0 + \sigma_t z\)

\(\mathbb E[\lVert h_\theta(x_t, t) - x_0 \rVert_2^2]\)

Forward process:

Backprop:

Corrupt data

\(t\in (t_n, T]\)

\(x_t = x_{t_n} + \sqrt{\sigma_t^2-\sigma_{t_n}^2} z_2\)

\(\mathbb E[\lVert \frac{\sigma_t^2 - \sigma_{t_n}^2}{\sigma_t^2} h_\theta(x_t,t) + \frac{\sigma_{t_n}^2}{\sigma_t^2} - x_{t_n} \rVert_2^2]\)

Ambient Diffusion

\(t=0\)

\(t=T\)

\(t=t_n\)

\(\mathbb E[\lVert h_\theta(x_t, t) - x_0 \rVert_2^2]\)

\(\mathbb E[\lVert \frac{\sigma_t^2 - \sigma_{t_n}^2}{\sigma_t^2} h_\theta(x_t,t) + \frac{\sigma_{t_n}^2}{\sigma_t^2}x_t - x_{t_n} \rVert_2^2]\)

Use clean data to learn denoisers for \(t\in(0,T]\)

Use corrupt data to learn denoisers for \(t\in(t_n,T]\)

Part 2b

Ambient Diffusion w/ Contraction

Protein Folding Case Study

Case Study: Protein Folding

Assumptions

1. Each corrupt data point contains additive gaussian noise up to some noise level \(t_n\)

2. \(t_n\) is known for each dataset or datapoint

\(t=0\)

\(t=T\)

\(t=t_n\)

Corrupt data: \(X_{t_n} = X_0 + \sigma_{t_n} Z\)

Case Study: Protein Folding

Corrupt Data

Clean Data

+  5 years

=

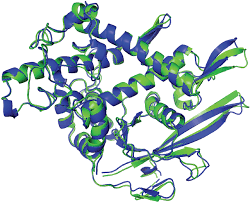
~100,000 solved protein structures

200M+ protein structures

Case Study: Protein Folding

Corrupt Data

Clean Data

\(X_0^{corrupt} \neq X_0^{clean} + \sigma_{t_n} Z\)

Breaks both assumptions:

  1. Corruption is not additive Gaussian noise
  2. Don't know \(t_n\) for each AlphaFold protein

\(X_0^{clean}\)

\(X_0^{corrupt}\)

Corrupt Data

Clean Data

Corrupt Data + Noise

For sufficiently high \(t_n\):   \(X_{t_n}^{corrupt} = X_0^{corrupt} + \sigma_{t_n} Z \approx X_0^{clean} + \sigma_{t_n} Z\)

\(X_{t_n}^{corrupt} = X_0^{corrupt} + \sigma_{t_n} Z\)

Key idea: Corrupt data further with Gaussian noise

Assumption 1: Contraction

\(X_0^{clean}\)

\(X_0^{corrupt}\)

\(X_{t_n}^{corrupt}\)

Key idea: Corrupt data further with Gaussian noise

For sufficiently high \(t_n\):   \(X_{t_n}^{corrupt} = X_0^{corrupt} + \sigma_{t_n} Z \approx X_0^{clean} + \sigma_{t_n} Z\)

\(x_0^{clean}\)

\(x_0^{corrupt}\)

\(t=0\)

\(t=T\)

\(t=t_n\)

Assumption 1: Contraction

For sufficiently high \(t_n\):   \(X_{t_n}^{corrupt} \approx X_0^{clean} + \sigma_{t_n} Z\)

\(P_{Y|X}\)

\(Y = X + \sigma_{t_n} Z\)

\(P_{X_0}^{clean}\)

\(Q_{X_0}^{corrupt}\)

\(P_{X_{t_n}}^{clean}\)

\(Q_{X_{t_n}}^{corrupt}\)

D(P_{X_0}^{clean}||Q_{X_0}^{corrupt}) \geq D(P_{X_{t_n}}^{clean}||Q_{X_{t_n}}^{corrupt})

Assumption 1: Contraction

\(\implies\) Adding noise makes the corruption appear Gaussian (Assumption 1)

  • Clean and corrupt data share coarse structure
  • Adding noise masks high-frequency differences, preserves low frequency similarities

\(x_0^{clean}\)

\(x_0^{corrupt}\)

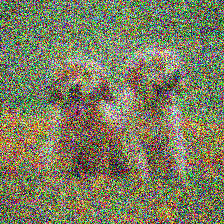
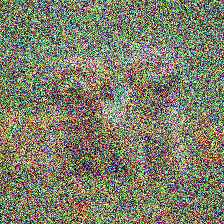
\(t=0\)

\(t=T\)

\(t=t_n\)

Assumption 1: Intuition

Assumption 2: Finding \(t_n\)

1. Train a "clean" vs "corrupt" classifier for all \(t \in [0, T]\)

2. For each corrupt data point, increase noise until the classification accuracy drops. This is \(t_n\).

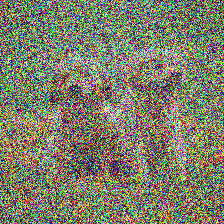
\(x_0^{clean}\)

\(x_0^{corrupt}\)

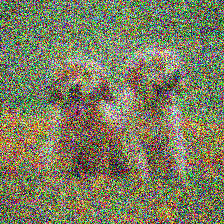
\(t=0\)

\(t=T\)

\(t=t_n\)

Training Algorithm

For each data point:

Clean data

\(x_t = x_0 + \sigma_t z\)

\(\mathbb E[\lVert h_\theta(x_t, t) - x_0 \rVert_2^2]\)

Forward process:

Backprop:

Corrupt data

\(x_t = x_{t_n} + \sqrt{\sigma_t^2-\sigma_{t_n}^2} z_2\)

\(x_{t_n} = x_0 + \sigma_{t_n} z_1\)

Contract data:

\(\mathbb E[\lVert \frac{\sigma_t^2 - \sigma_{t_n}^2}{\sigma_t^2} h_\theta(x_t,t) + \frac{\sigma_{t_n}^2}{\sigma_t^2} - x_{t_n} \rVert_2^2]\)

Part 3

Interpretations

Frequency Domain Interpretation

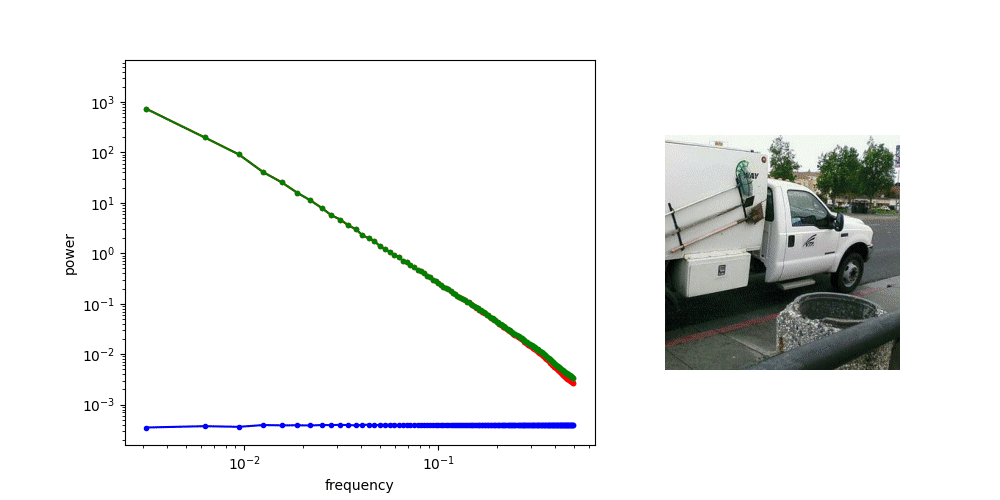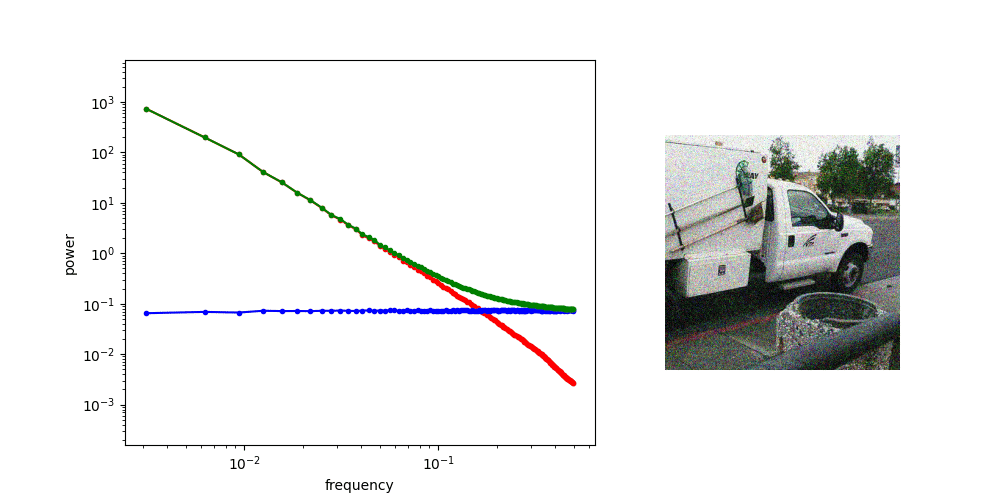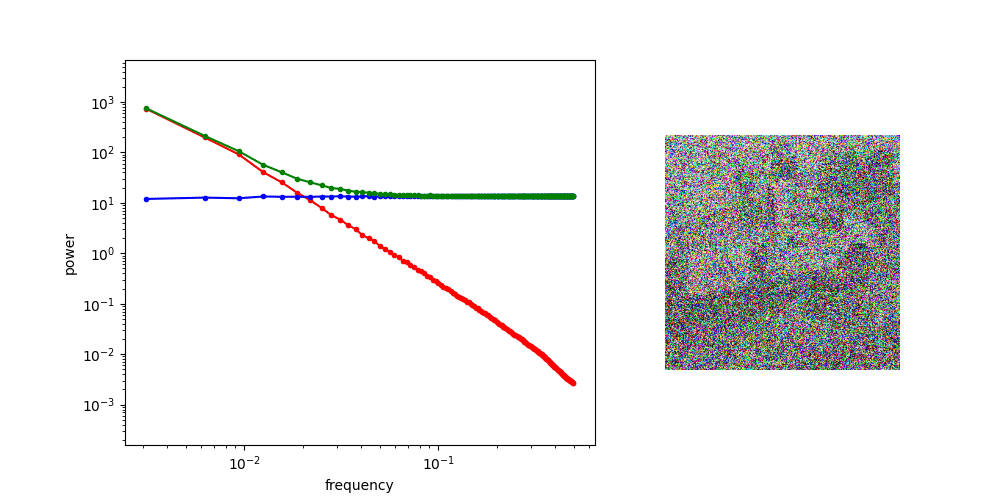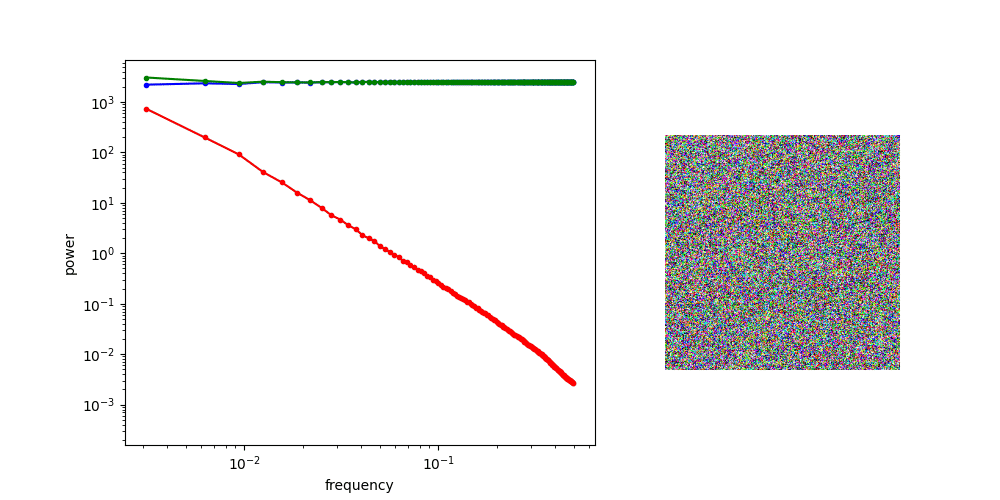
Diffusion is AR sampling in the frequency domain

https://sander.ai/2024/09/02/spectral-autoregression.html

Frequency Domain Interpretation*

\(t=0\)

\(t=T\)

\(t=t_n\)

Low Frequency

High Frequency

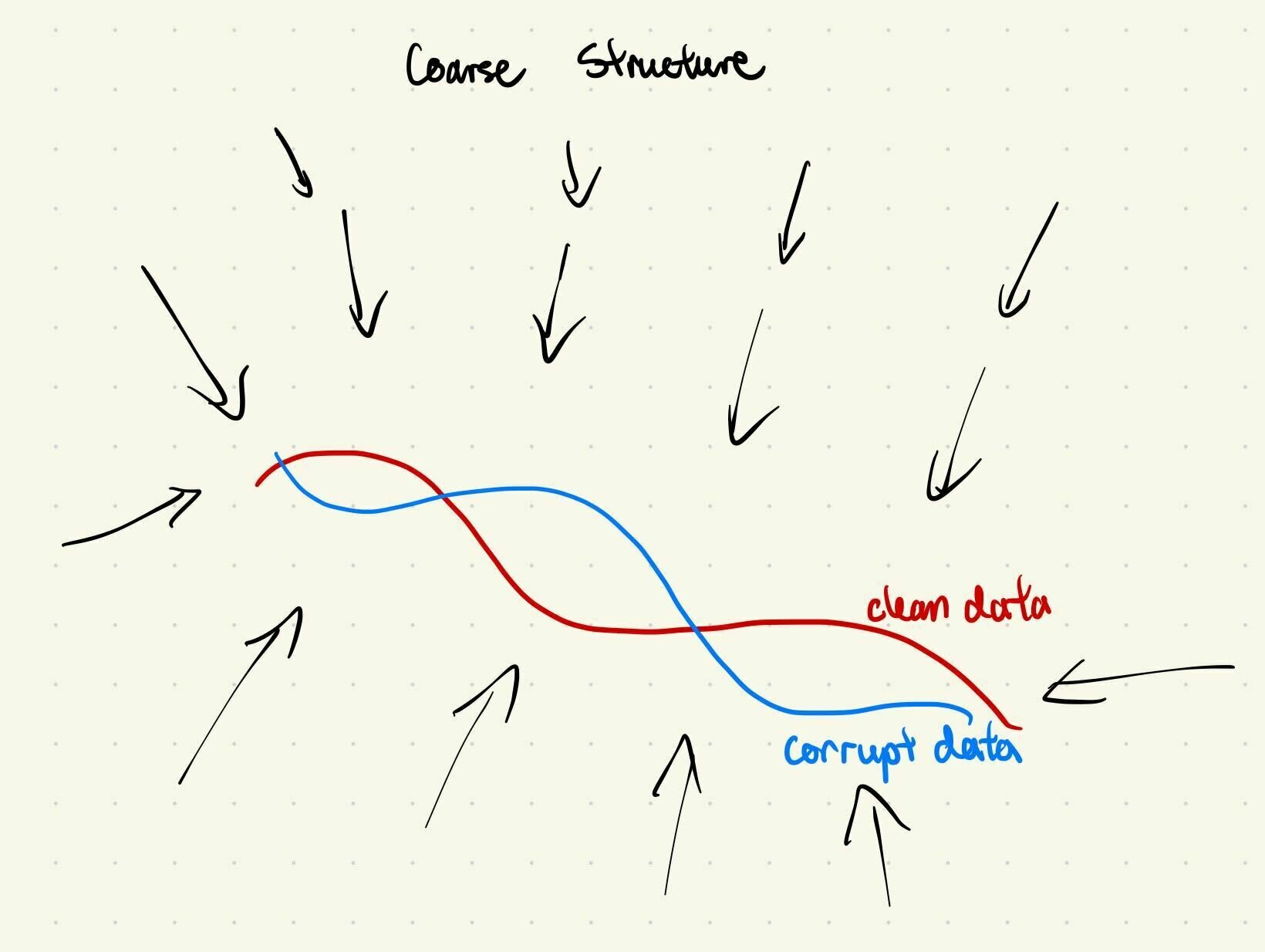
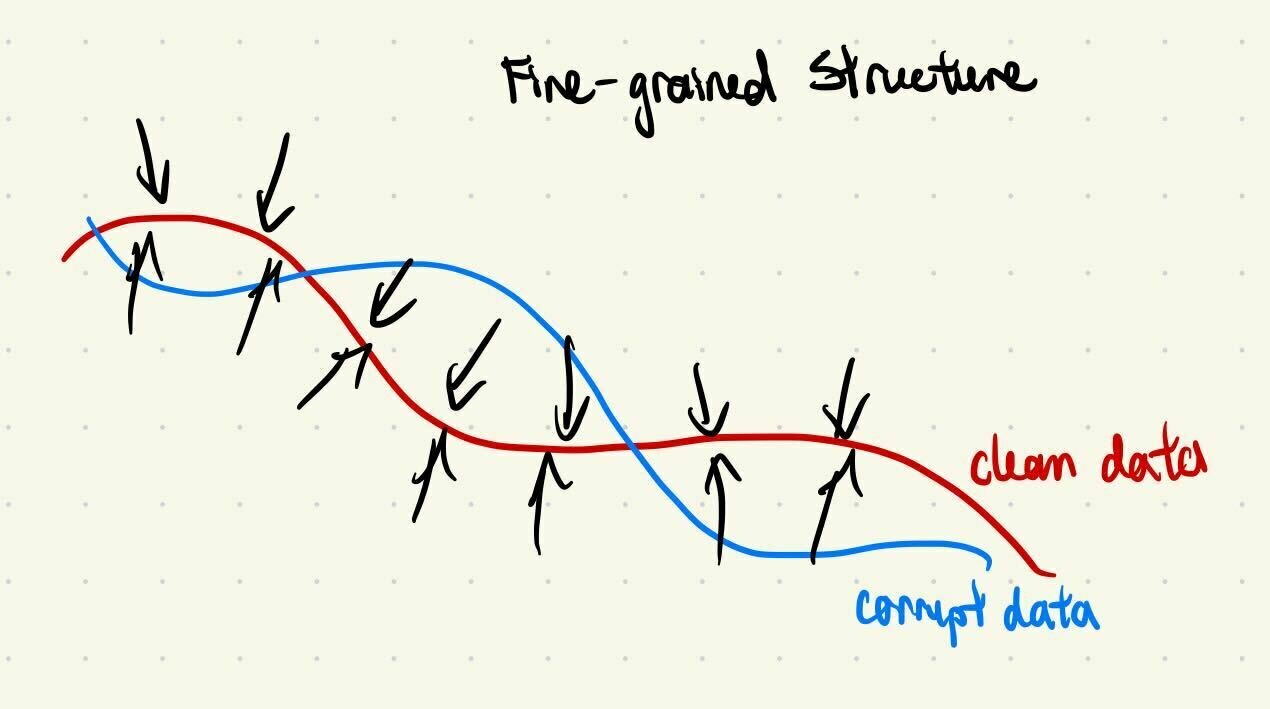
Coarse Structure

Fine-grained Details

* assuming power spectral density of data is decreasing

Frequency Domain Interpretation

\(t=0\)

\(t=T\)

\(t=t_n\)

\(\mathbb E[\lVert h_\theta(x_t, t) - x_0 \rVert_2^2]\)

\(\mathbb E[\lVert \frac{\sigma_t^2 - \sigma_{t_n}^2}{\sigma_t^2} h_\theta(x_t,t) + \frac{\sigma_{t_n}^2}{\sigma_t^2}x_t - x_{t_n} \rVert_2^2]\)

Low Freq

High Freq

Clean & corrupt data share the same "coarse structure"

Learn coarse structure from all data

Learn fine-grained details from clean data only

i.e. same low frequency features

Clean Data

Corrupt Data

Robotics Hypothesis

Hypothesis: Robot data shares low-frequency features, but differ in high frequency features

Clean & corrupt data share the same "coarse structure"

i.e. same low frequency features

Low Frequency

  • Move left or right
  • Semantics & language
  • High-level decision making

Learn with Open-X, AgiBot, sim, clean data, etc

High Frequency

  • Environment physics/controls
  • Task-specific movements
  • Specific embodiment

Learn from clean task-specific data

"Manifold" Interpretation

Diffusion is Euclidean projection onto the data manifold

Assumption: The clean and corrupt data manifolds lie in a similar part of space, but differ in shape

"Manifold" Interpretation

Diffusion is Euclidean projection onto the data manifold

Large \(\sigma_t\)

Both clean and corrupt data project to close to the clean data manifold

"Manifold" Interpretation

Diffusion is Euclidean projection onto the data manifold

Small \(\sigma_t\)

Use clean data to project onto the clean data manifold

Part 4

Robotics??

Robotics

Open-X

 expert robot teleop

 robot teleop

simulation

"corrupt"

"clean"

Start by exploring ideas inspired by Ambient Diffusion on sim-and-real cotraining

Robotics: Sim-and-Sim Cotraining

Corrupt Data (Sim): \(\mathcal D_S\)

Clean Data (Real): \(\mathcal D_T\)

Replayed GCS plans in Drake

Sources of corruption: (non-Gaussian...)

  • Physics gap
  • Visual gap
  • Action gap

Teleoperated demos in a target-sim environment

... sorry no video :(

Robotics Idea 1: Modified Diffusion

  • Assume all simulated data points in \(\mathcal D_S\) are corrupted with some fixed level \(t_n\)
  • For \(t > t_n\): train denoisers with clean and corrupt data
  • For \(t \leq t_n\): train denoisers with only clean data
  • Use regular DDPM loss (i.e. not ambient loss)
    • Since the sim_data \(\neq\) real_data + noise

Training:

Robotics Idea 1: Modified Diffusion

\(t=0\)

\(t=T\)

\(t=t_n\)

\(\mathbb E[\lVert h_\theta(x_t, t) - x_0^{clean} \rVert_2^2]\)

\(\mathbb E[\lVert h_\theta(x_t, t) - x_0^{corrupt} \rVert_2^2]\)

Low Freq

High Freq

Learn with all data

Learn with clean data

Clean Data

Corrupt Data

Intuition: mask out high-frequency components of "corrupt" data

Robotics Idea 1

Robotics Idea 2: Ambient w/o Contraction

\(t=0\)

\(t=T\)

\(t=t_n\)

\(\mathbb E[\lVert h_\theta(x_t, t) - x_0^{clean} \rVert_2^2]\)

Low Freq

High Freq

Learn with all data

Learn with clean data

Clean Data

Corrupt Data

Assume \(X_0^{corrupt} = X_{t_n}^{clean} = X_0^{clean} + \sigma_{t_n} Z\)

(NOT TRUE)

\(\mathbb E[\lVert \frac{\sigma_t^2 - \sigma_{t_n}^2}{\sigma_t^2} h_\theta(x_t,t) + \frac{\sigma_{t_n}^2}{\sigma_t^2}x_t - x_0^{corrupt} \rVert_2^2]\)

Robotics Idea 1

Results: Idea 1

  • 50 clean (real) demos
  • 2000 corrupt (sim) demos
  • 200 trials each

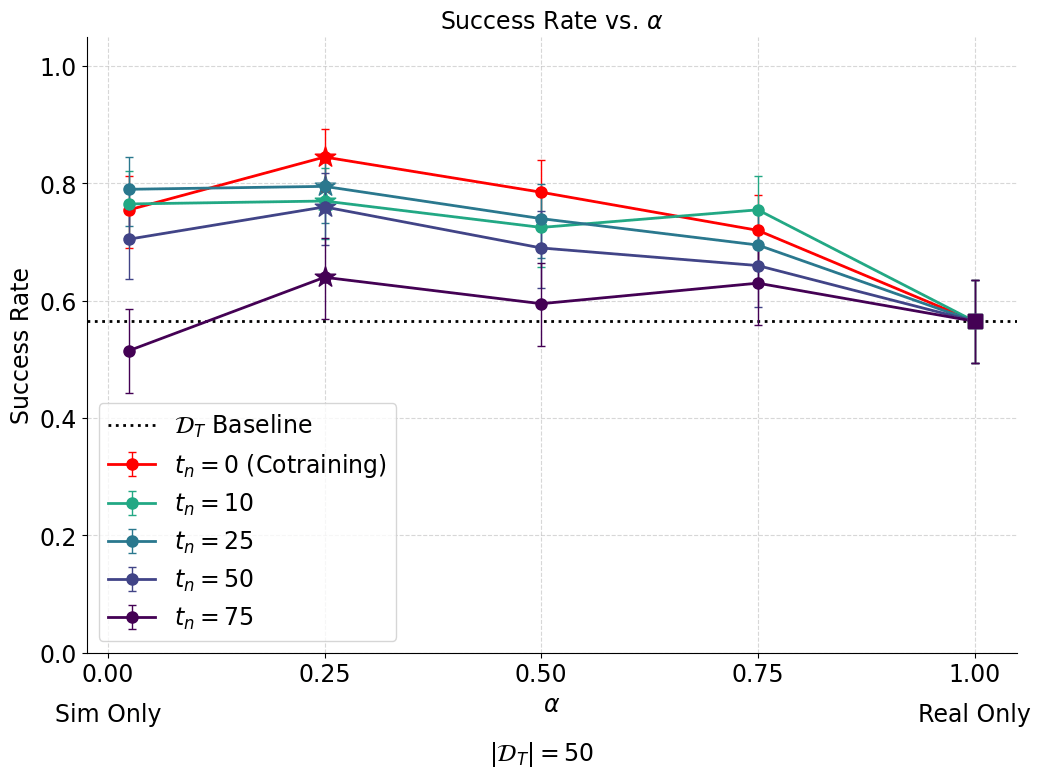
Results are currently worse than the cotraining baseline :(

Robotics Idea 1

Discussion: Idea 1

  • Ambient diffusion loss rescaling
  • Real and sim data are too similar at all noise levels
    • \(\implies\) no incentive to mask out high-frequency components of "corrupt" data
    • Will potentially find more success using Open-X, AgiBot, etc
  • Image conditioning is sufficient to disambiguate sampling from clean (real) vs corrupt (sim)

\(\mathbb E[\lVert \frac{\sigma_t^2 - \sigma_{t_n}^2}{\sigma_t^2} h_\theta(x_t,t) + \frac{\sigma_{t_n}^2}{\sigma_t^2}x_t - x_{t_n} \rVert_2^2]\)

\(\mathbb E[\lVert h_\theta(x_t,t) + \frac{\sigma_{t_n}^2}{\sigma_t^2-\sigma_{t_n}^2}x_t - \frac{\sigma_t^2}{\sigma_t^2 - \sigma_{t_n}^2}x_{t_n} \rVert_2^2]\)

Ambient Loss

"Rescaled" Ambient Loss

... blows up for small \(\sigma_t\)

Robotics Idea 1

Discussion: Idea 1

  • Ambient diffusion loss rescaling
  • Real and sim data are too similar at all noise levels
    • \(\implies\) no incentive to mask out high-frequency components of "corrupt" data
    • Will potentially find more success using Open-X, AgiBot, etc
  • Image conditioning is sufficient to disambiguate sampling from clean (real) vs corrupt (sim)
  • Hyperparameter sweep

Robotics Idea 1

Results: Idea 2

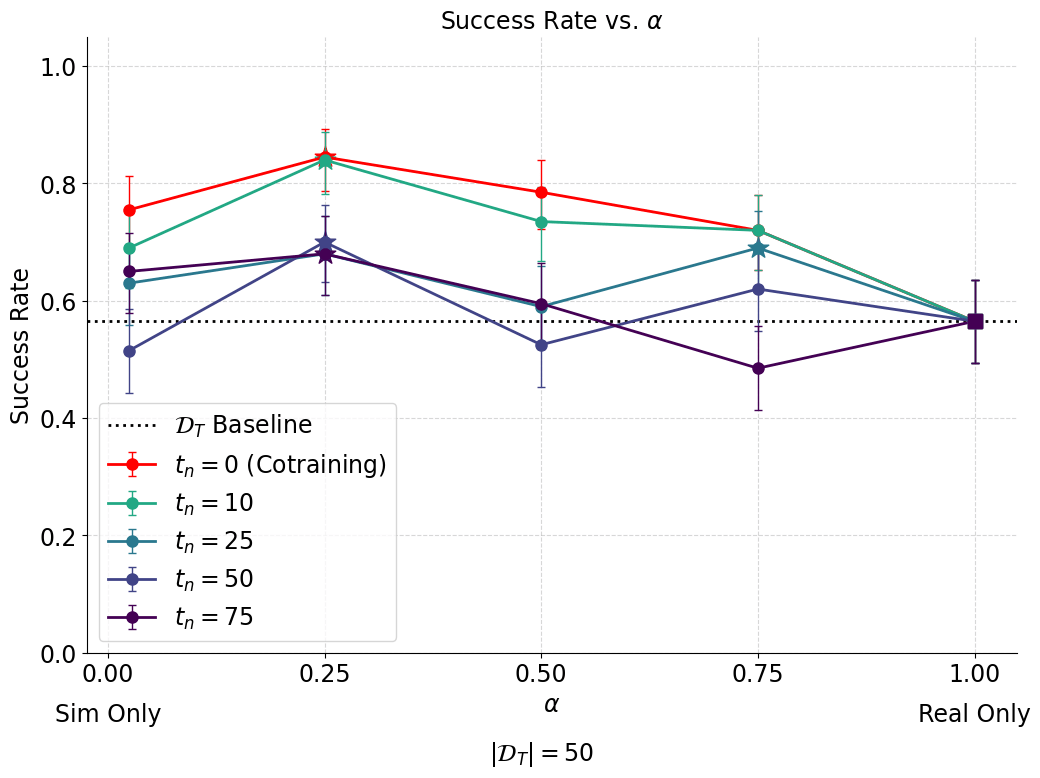
Worse than idea 1, but this was expected

Assume \(X_0^{corrupt} = X_{t_n}^{clean} = X_0^{clean} + \sigma_{t_n} Z\)

(NOT TRUE)

Robotics Idea 1

Idea 3: Ambient w/ Contraction

1. Train a binary classifier to distinguish sim vs real actions

2. Use the classifier to find \(t_n\) for all sim actions in \(\mathcal D_S\)

3. Noise all sim actions to \(t_n\):

\(X_{t_n}^{corrupt} = X_0^{corrupt} + \sigma_{t_n} Z\)

\(\approx X_0^{clean} + \sigma_{t_n} Z\)

4. Train with ambient diffusion and \(t_n\) per datapoint

*same algorithm as SOTA protein folding

Robotics Idea 1

Idea 3: Ambient w/ Contraction

1. Train a binary classifier to distinguish sim vs real actions

2. Use the classifier to find \(t_n\) for all sim actions in \(\mathcal D_S\)

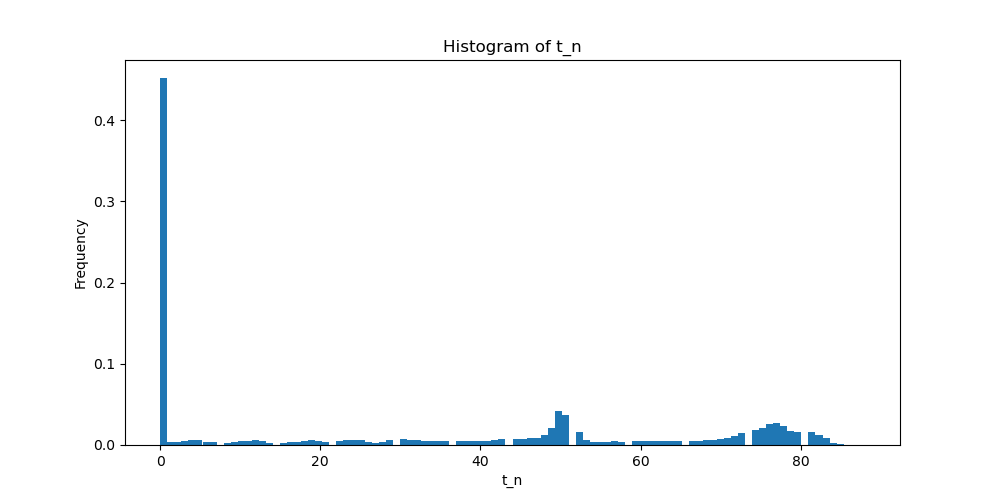
\(t_n\) = 0 for 40%+ of action sequences... \(\implies\) sim data is barely corrupt

Robotics Idea 1

Idea 3: Ambient w/ Contraction

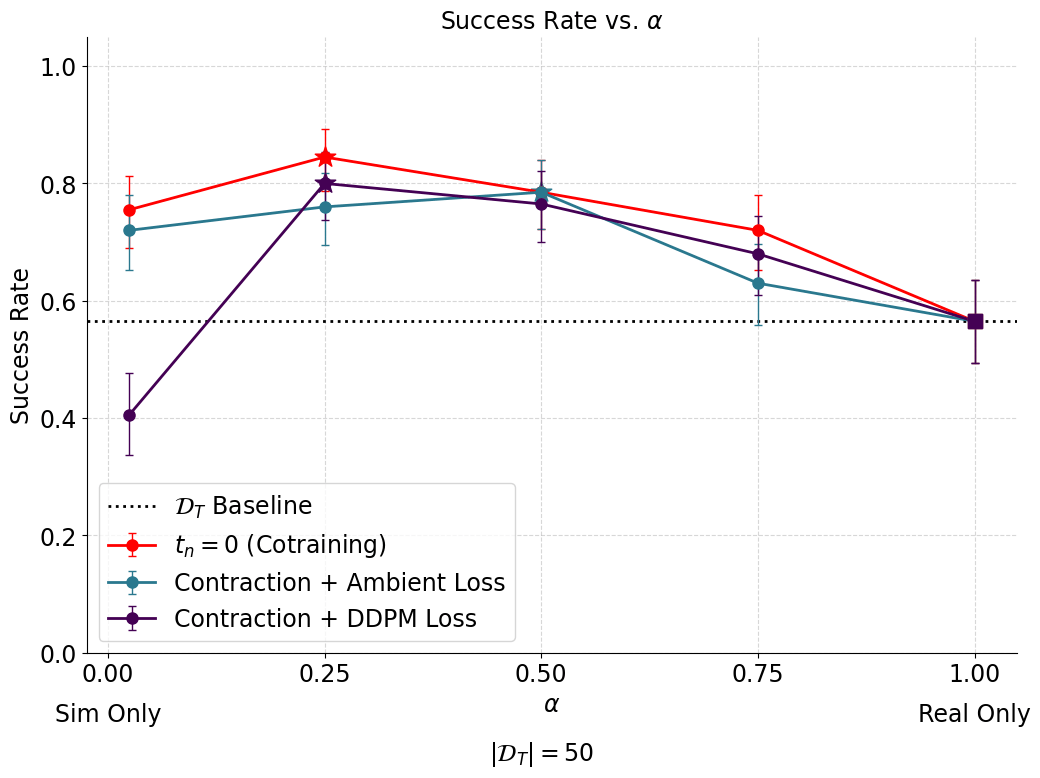
Robotics Idea 1

Idea 4: ... but first recall idea 1

\(t=0\)

\(t=T\)

\(t=t_n\)

\(\mathbb E[\lVert h_\theta(x_t, t) - x_0^{clean} \rVert_2^2]\)

\(\mathbb E[\lVert h_\theta(x_t, t) - x_0^{corrupt} \rVert_2^2]\)

Low Freq

High Freq

Learn with all data

Learn with clean data

Clean Data

Corrupt Data

Robotics Idea 1

Idea 4: Different \(\alpha_t\) per \(t\in (0, T]\)

\(t=0\)

\(t=T\)

Low Freq

High Freq

Clean Data

Corrupt Data

  • Train with different data mixtures \(\alpha_t\) at different noise levels

\(\mathbb E[\lVert h_\theta(x_t, t) - x_0^{clean} \rVert_2^2]\)

\(\mathbb E[\lVert h_\theta(x_t, t) - x_0^{corrupt} \rVert_2^2]\)

\(\alpha_T\)

\(\alpha_0\)

Robotics Idea 1

Idea 4: Different \(\alpha_t\) per \(t\in (0, T]\)

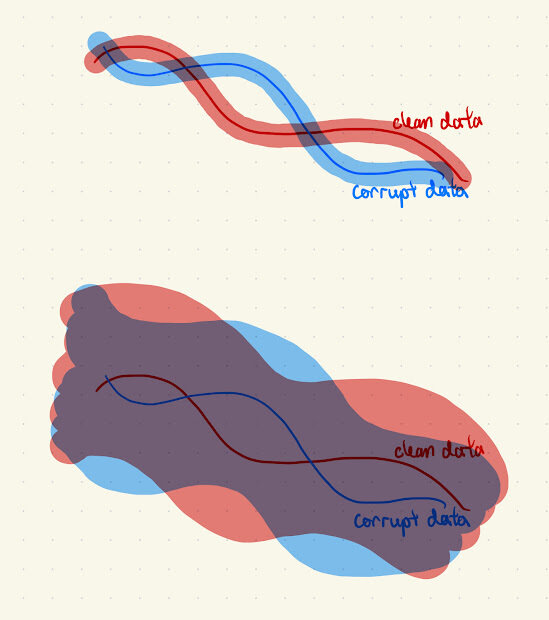
\(D(\red{p^{clean}_{\sigma_t}}||\blue{p^{corrupt}_{\sigma_t}})\) is large

\(\implies\) sample more clean data

Low noise levels

(small \(\sigma_t\))

High noise levels

(large \(\sigma_t\))

\(D(\red{p^{clean}_{\sigma_t}}||\blue{p^{corrupt}_{\sigma_t}})\) is small

\(\implies\) sample more corrupt data

Robotics Idea 1

Next Directions

  • Try to improve results for all 4 ideas on planar pushing

 

  • Try ambient diffusion related ideas for cotraining from Open-X or AgiBot

Robotics Idea 1

Thoughts

Motivating ideas for ambient diffusion

  • Noise as partial masking (mask out high frequency corruption)
  • Clean and corrupt distributions are more similar at high noise levels

 

Motivating ideas could be useful for robotics, but the exact Ambient Diffusion algorithm might not??

Thank you!