Unifying Perspectives on Diffusion

RLG Short Talk

May 3, 2024

Adam Wei

Interpretations of Diffusion

Goal: Show how the different interpretations of diffusion are connected.

Diffusion

Sohl-Dickstein et al

DDPM

Ho et al

SMLD

Song et al

SDE

Song et al

Projection

Permenter et al

2015

2019

2021

2023

Denoising

Score-based

Optimization

2020

What this presentation is not...

  • Not a deep dive into the papers
  • Not a rigorous mathematical presentation
  • Not about how to train diffusion policies or score-matching

Goal: Show how the different interpretations of diffusion are connected.

SDE Interpretation

Summary

\epsilon_\theta(x,t) \propto -\nabla_x \log p_t(x)

2. Score-based and denoiser approaches are discrete instantiations of the SDE approach

1. Both SMLD and DDPM learn the score function of the noisy distributions.

Interpretations of Diffusion Policy

Diffusion

Sohl-Dickstein et al

DDPM

Ho et al

SMLD

Song et al

SDE

Song et al

Projection

Permenter et al

2015

2019

2021

2023

Denoising

Score-based

Optimization

2020

Goal: Show how the different interpretations of diffusion are connected.

SMLD: Langevin Dynamics (1/5)

X_{t+h} = X_t + h\red{\nabla \log p(X_t)} + \sqrt{2h} \epsilon

Intuition: On each step..

Key Takeaway:                              ​     under regularity conditions

X_t \rightarrow X \sim p
  1. Move in a direction that increases log probability
  2. Add Gaussian noise (prevent collapse onto peaks of p)

"Score Function"

Goal: Sample from some distribution p

SMLD: Langevin Dynamics (2/5)

"Gradient ascent with Gaussian noise"

https://www.peterholderrieth.com/blog/2023/Langevin-Dynamics-An-introduction-for-Machine-Learning-Engineers/

SMLD: Algorithm (3/5)

1. Construct sequence of noised distributions:

q_{\sigma_1},\ ... \ ,q_{\sigma_L}
\begin{aligned} &q_{\sigma_L} \approx p_{data} \\ &q_{\sigma_L} \approx \text{Gaussian} \end{aligned}

2. Learn 

s_\theta(X, \sigma_i) \approx \nabla \log q_{\sigma_i}(X) \ \forall i

3. Sample from annealed Langevin Dynamics 

X_{i-1} = X_i + h\red{s_\theta(X_i,\sigma_i)} + \sqrt{2h} \epsilon

SMLD: Algorithm (4/5)

X_{i-1} = X_i + h\red{s_\theta(X_i,\sigma_i)} + \sqrt{2h} \epsilon
X_{t+s} = X_t + h\red{\nabla \log p(X_t)} + \sqrt{2h} \epsilon

Advantages

  1. Faster convergence
  2. Better learned scores
\approx \nabla \log q_{\sigma_i}(X)

SMLD: Results (5/5)

SMLD: Connection to control... (Bonus)

1. Design a trajectory in distribution space

q_{\sigma_1},\ ... \ ,q_{\sigma_L}

2. Use Langevin Dynamics to track this trajectory

X_{i-1} = X_i + h\red{s_\theta(X_i,\sigma_i)} + \sqrt{2h} \epsilon

TODO: DRAW IMAGE

Interpretations of Diffusion Policy

Diffusion

Sohl-Dickstein et al

DDPM

Ho et al

SMLD

Song et al

SDE

Song et al

Projection

Permenter et al

2015

2019

2021

2023

Denoising

Score-based

Optimization

2020

Goal: Show how the different interpretations of diffusion are connected.

DDPM: Overview (1/6)

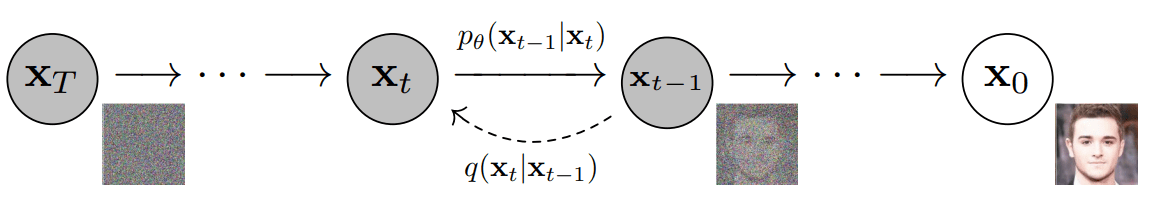
Forward Process: Noise the data

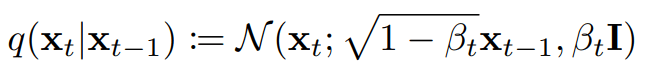
Backward Process: Denoising

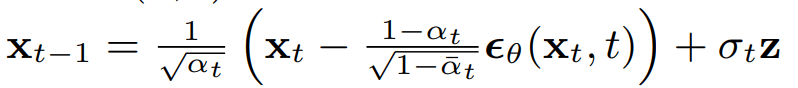
DDPM: Results (2/6)

DDPM vs SMLD (3/6)

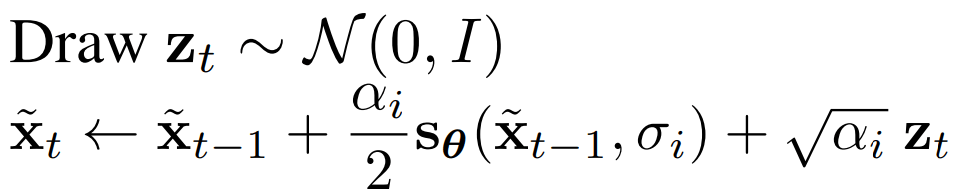
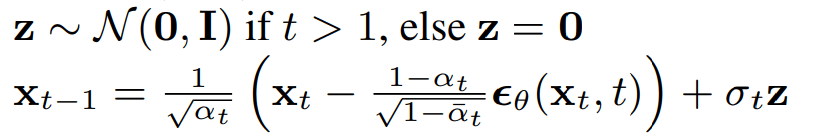
SMLD Sampling:

DDPM Sampling:

Screenshots from the papers. Notation is not same!!

DDPM vs SMLD (4/6)

SMLD Loss

DDPM Loss

Screenshots of original loss functions. Notation is not same!!

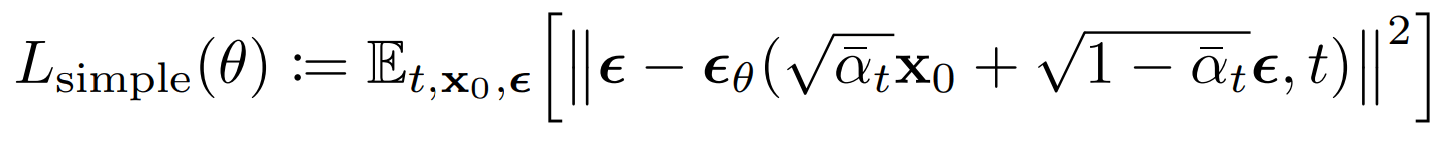
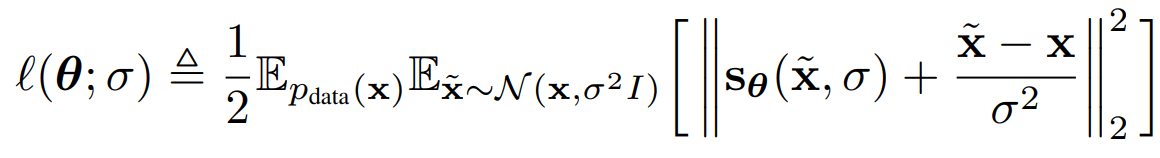
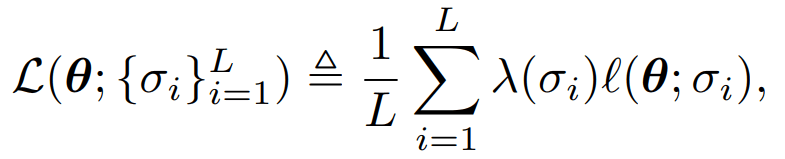
DDPM vs SMLD (5/6)

SMLD Loss*:

DDPM Loss*:

\mathbb{E}_{\blue{t,x_0,\epsilon}}[\lambda(t)\lVert \red{\epsilon_\theta(\sqrt{\bar{\alpha_t}}x_0 + \sigma_t\epsilon,\ t)} - \green{\epsilon} \rVert_2^2]

*Rewritten loss functions with severe abuse of notation to highlight similarities.

\mathbb{E}_{\blue{t,x_0,\epsilon}} [\lambda(\sigma_t)\lVert \red{s_\theta(x_0 + \sigma_t\epsilon,\ \sigma_t)} + \green{\frac{\epsilon}{\sigma_t}} \rVert_2^2]
x_t
x_t

DDPM: Connection to Score-Matching (6/6)

Key Takeaway

\nabla \log p_t(x_t) = -\frac{1}{\sqrt{1-\bar{\alpha_t}}}\epsilon_0 = -\frac{1}{\sqrt{\mathbb{V}[X_t | X_0]}}\epsilon_0
\implies \epsilon_\theta(x,t) \approx -\sqrt{\mathbb{V}[X_t | X_0]}\red{\nabla \log p_t(x)}

Proofs...

[1] Understanding Diffusion Models: A Unified Perspective

[2] Peter Holderrieth's Blog

SDE Interpretation

Interpretations of Diffusion Policy

Diffusion

Sohl-Dickstein et al

DDPM

Ho et al

SMLD

Song et al

SDE

Song et al

Projection

Permenter et al

2015

2019

2021

2023

Denoising

Score-based

Optimization

2020

Goal: Show how the different interpretations of diffusion are connected.

SDE Interpretation

SDE: Overview (1/8)

SMLD/DDPM: Noise and denoise in discrete steps.

 

SDE: Noise and denoise according to continuous SDEs

SDE Interpretation

SDE: Overview (2/8)

Key Takeaway: SMLD and DDPM are discrete instances of the SDE interpretation!

SDE Interpretation

SDE: Ito-SDE (3/8)

dX =f(X,t)dt+g(t)dW

[1] Bernt Øksendal, 2003 [2] Brian D O Anderson, 1982

1. If f and g are Lipschitz, the Ito-SDE has a unique solution [1].

2. The reverse-time SDE is [2]:

dX = [f(X,t)-g^2(t)\red{\nabla_x\log p_t(X)}]dt + g(t)d\bar{W}
\begin{aligned} &X(\cdot) \text{ is a stochastic process }\\ &X(t) \text{ is a random variable} \\ \end{aligned}

"Ito-SDE"

SDE Interpretation

SDE: Algorithm (4/8)

1. Define f and g s.t. X(0) ~ p transforms into a tractable distribution, X(T)

dX =f(X,t)dt+g(t)dW

2. Learn

s_\theta(x, t) \approx \nabla_x \log p_{X_t}(x)

3. To sample:

 - Draw sample x(T)

 - Reverse the SDE until t=0

SMLD/DDPM

dX = [f(X,t)-g^2(t)\red{s_\theta(X,t)}]dt + g(t)d\bar{W}

SDE Interpretation

SDE: SMLD (5/8)

x_i = x_{i-1} + \sqrt{\sigma_i^2 - \sigma_{i-1}^2}z_{i-1}

Forward (N-steps):

x(t+ \Delta t) = x(t) + \sqrt{\sigma^2(t + \Delta t) - \sigma^2(t)}z(t)

SDE Interpretation

SDE: SMLD (6/8)

x(t+ \Delta t) = x(t) + \sqrt{\sigma^2(t + \Delta t) - \sigma^2(t)}z(t)
\begin{aligned} &N \rightarrow \infty \\ &\Delta t \rightarrow 0 \end{aligned}
dX = \sqrt{\frac{d[\sigma^2(t)]}{dt}}dW
\implies
\begin{aligned} &f(x,t) = 0 \\ &g(t) = \sqrt{\frac{d[\sigma^2(t)]}{dt}} \end{aligned}

SDE Interpretation

SDE: DDPM (7/8)

x_i = \sqrt{1-\beta_i}x_{i-1} + \sqrt{\beta_i}z_{i-1}

Forward (N-steps):

x(t+ \Delta t) = \sqrt{1-\beta(t+\Delta t)\Delta t}x(t) + \sqrt{\beta(t+\Delta t)\Delta t}z(t)
\begin{aligned} &N \rightarrow \infty \\ &\Delta t \rightarrow 0 \\ \end{aligned}
dX = -\frac{1}{2}\beta(t)Xdt + \sqrt{\beta(t)}dW
\implies
\begin{aligned} &f(x,t) = -\frac{1}{2}\beta(t)x \\ &g(t) = \sqrt{\beta(t)} \end{aligned}

SDE Interpretation

SDE: Summary (8/8)

\begin{aligned} &f(x,t) = 0 \\ &g(t) = \sqrt{\frac{d[\sigma^2(t)]}{dt}} \end{aligned}
dX =f(X,t)dt+g(t)dW
dX = [f(X,t)-g^2(t)\red{\nabla_x\log p_t(X)}]dt + g(t)d\bar{W}

SDE Interpretation:

Forward:

Reverse:

\begin{aligned} &f(x,t) = -\frac{1}{2}\beta(t)x \\ &g(t) = \sqrt{\beta(t)} \end{aligned}

SMLD

DDPM

SDE Interpretation

Summary

\epsilon_\theta(x,t) \propto -\nabla_x \log p_t(x)

2. Score-based and denoiser approaches are discrete instantiations of the SDE approach

1. Both SMLD and DDPM learn the score function of the noisy distributions.

SDE Interpretation

Resources

Papers: Sohl-Dickstein, SMLD, DDPM, SDE, Permenter, Understanding Diffusion Models

Blogs: Lillian Weng, Yang Song, Peter E. Holderrieth

Tutorials: Yang Song, "What are Diffusion Models"

Diffusion in Robotics: https://github.com/mbreuss/diffusion-literature-for-robotics

Thank you!