A Solution, a Clicker, and the Zero Product Property Walk into a Bar...
Anurag Katyal
Professor I, Mathematics
Palm Beach State College, FL
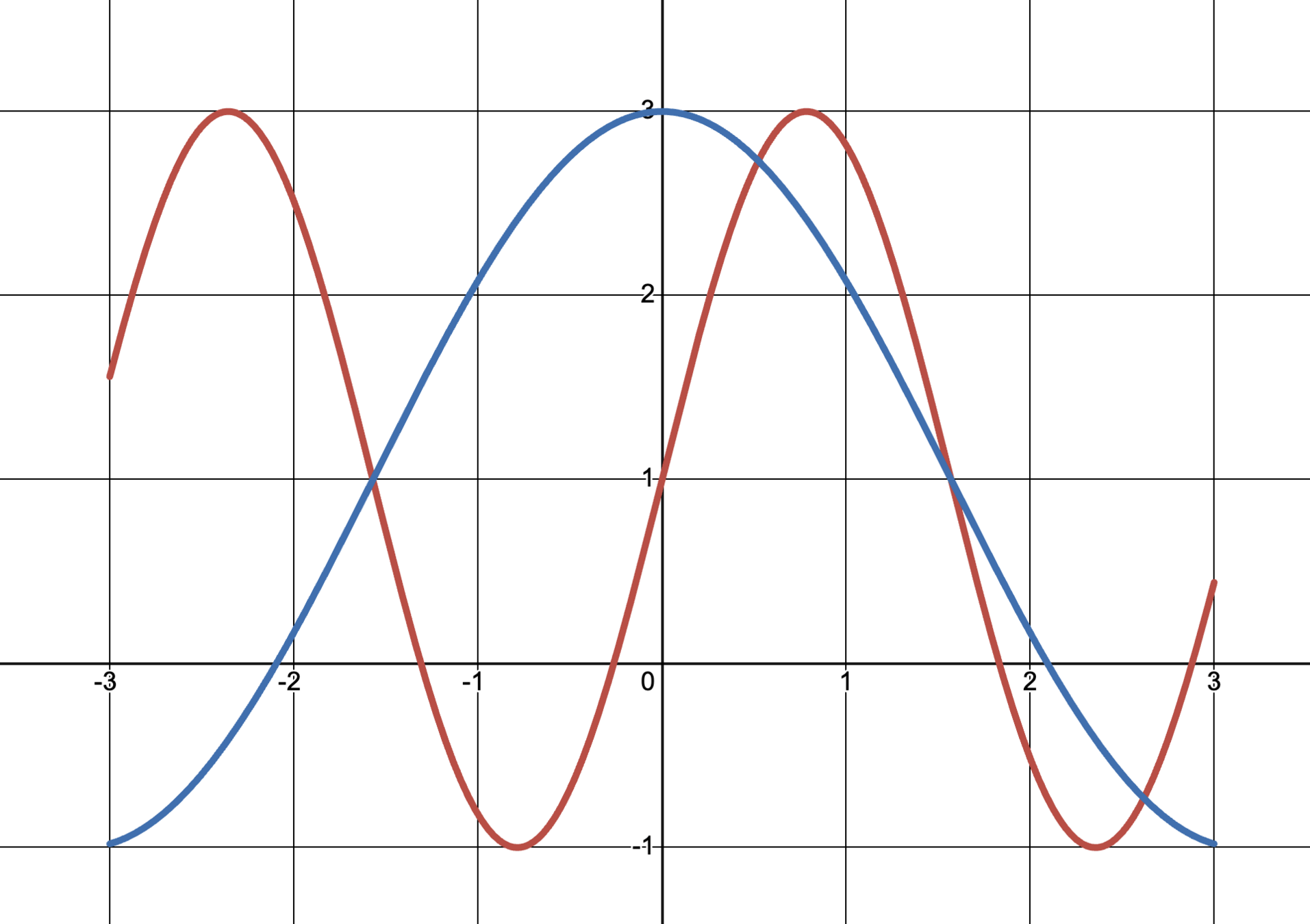
Q1. How many solutions does the above system of equations have in \([-3,3]\)?
Q2. Find the value(s) of \(k\) such that the line \(5 x+y=-9\) is tangent to the graph of \(f(x)=2 x^2+k x-1\).

The problem
My students don't yet understand <y>, deeply, because they don't <do x> first.
-Anonymous Faculty
My students don't yet deeply understand what a solution is because don't verify their answers to see if they are solutions.
– Anurag

Heat
Oxygen
Team Based Inquiry Learning
A (Potential) Solution
The Serendipitous Fire Triangle of Math™
(circa Summer 2023)
Active Learning Studios
Doenet
Fuel
Head
Head
Body
Tail
Body
Tail
Tail
Body
Tail
Reorder content and Delivery

Week 1, Day 2

Week 15, Day 1

1
Students don't check to see if their answers are solutions.
2
Students don't deeply understand what a solution is.
3
Students favor memorizing different algorithms for seemingly different types of problems.
5
Bad things happen on quizzes.
4
Students miss the modularity of the solution pathways.
6
Very bad things happen on tests/in following courses.
The Problem(s)
- (Tail)Verify solutions
- (Body and Tail) Solve equations and verify solutions
- (Head, Body and Tail) Translate English to Math, solve equations, and verify solutions
The New way
- (Head) Translate English to Math
- (Body) Solve equations
- (Tail) Verify Solutions
- (!!!) At the start of the course, all answers are solutions.
The Old Way
Head
Head
Body
Tail
Body
Tail
Tail
Body
Tail
Reorder content and Delivery
Team BAsed Inquiry Learning
-
Permanent teams selected by the instructor
-
Students held accountable through Readiness Assurance Process
-
Students receive frequent and immediate feedback
-
Teams work collaboratively on activities.
Students Collaborate
(while i listen)




Hands must remain in pockets (As much as possible)
TBIL Activities
Significant Problem
Same Problem
Simultaneous Report
Specific Choice
-
Free and open-source interactive activities
-
Immediate feedback in class
-
Open-ended response
-
Try different approaches
Collaborative Research: Empowering faculty to run online learning experiments


So...what exactly is a solution?

The Activity
What do students think?
- 4 Intermediate Algebra sections (76 students)
- Week 1, Fall 2023 - "What do you think it means for a number to be a solution to an equation?"
- 8 out of 72 (~11%): "If you substitute a solution into an equation, it satisfies the equation, making the equation true."
- 12 out of 72 students (~17%) alluded to substituting a solution into an equation but did not expand further.
Intro/Test 1
- Week 1 - Students engage with Doenet activity and scored an average of 87.13%.
- Week 4 - Solve \(\color{blue}\frac{41}{9}=\frac{5}{2}\left(x+\frac{2}{3}\right)-\frac{1}{3} x\) for \(x\). Explain whether the number you found for \(x\) was a solution to the equation.
- 17 out of 74 students (~23%) were awarded at least half credit.
Test 2
-
Week 7 - Which of the following values are solutions to the inequality \(\color{blue}9 \leq 3 x+4\) ?
I. \(\color{blue}-7\) II. \(\color{blue}8\) III. \(\color{blue}2\) - Students encouraged but not required to revisit the activity from the start of the course.
- 59 out of 74 students (~80%) were awarded at least half credit.
Test 3
- Week 11 - Solve \(\color{blue}\frac{n}{n+3}+\frac{1}{n-4}=\frac{6-5 n}{n^2-n-12}\) for \(n\).
- Initially asked to work on this problem independently.
- Without being prompted, 36 out of 51 students (~71%) verified \(n=1\) was the only solution to the equation and also wrote an explanation.
Final Exam
- Week 15 - Solve \(\color{blue}\sqrt{2 x+2}=3+\sqrt{2 x-1}\) for \(x\).
- 33 out of 50 students (66%) correctly identified the equation has no solutions. 4 more students solved the question correctly and verified the candidates but did not explain their findings.
- Historically, maximum of ~25% with semesters with at least 65 students and average of ~19%.
- Passing rates went up 20% from 35% to 55%.
〞
I personally liked Doenet activities because it helped me get hands on learning as a group. The way the course was set up allowed me to open up in ways I haven’t before and also hear my peers talk. It also broke down steps that helped answer complex questions later in the semester.
– Intermediate Algebra student
〞
I hate this man so much. He could have just taught in a normal way.
– Intermediate and College Algebra student
I'll see him in College Algebra.
He tricked me into liking math.

\(100\%\)
(n=6)
Let's take a walk...

Acknowledgements
- Doenet (NSF Award # 1915363)
- PI - Duane Nykamp, Uni. of Minnesota
- Doenet Learning Experiment Mini-Grant
- www.doenet.org
- Team Based Inquiry Learning (NSF Award # 2011807)
- PI - Steven Clontz, Uni. of South Alabama
- www.tbil.org
Sabbatical until May 2025.
Please reach out if you have ideas or suggestions!

