微積分
presenter: fan of Aaw
DISCLAIMER:
本次課程切入的角度並非嚴謹的數學證明
有一個* 在旁邊的話表示唬爛這個說法技術上來說不對
而是為了有一個整個領域的大尺度Overview
目的是讓你們能夠在看研究或新東西時
有ㄧ點常識讓你們能夠更好理解酷東西
極限
微積分
- 微分+積分*
- 研究連續性的東西
- 在自然科學和數學本身都很有用
很小的東西
圓型面積?
抓住這個直覺
把一個東西逼近到無限大(小)
\lim\limits_{x \to \infty} f(x)
把他想像成一個非常靠近c的數
嚴謹的定義利用 Epsilon-Delta Definition
\lim\limits_{x \to c} f(x)
例子
\lim\limits_{x\to 0} \frac{\sin{x}}{x}
\space\space\space
\\
\lim\limits_{x\to 0}\frac{1}{x} \space\space\space\space\space\space\space
\\
\lim\limits_{x\to \infty}\frac{1}{x}\space\space\space\space\space\space\space
\\
\lim\limits_{x\to \infty}\frac{x^2+7122}{2x^2}
微分
將一個函數變成另一個函數
\frac{d}{dx}f(x) = f^{'}(x) = \frac{df}{dx} =
\\ \\ \\ \lim\limits_{h\to 0}{\frac{f(x+h)-f(x)}{h}}
幾何意義
f(x)在x處切線的斜率
運算性質
\frac{d}{dx}(f(x)+g(x)) = \frac{d}{dx}f(x)+\frac{d}{dx}g(x)
\frac{d}{dx}(f(x)g(x)) = f(x)\frac{dg}{dx}+g(x)\frac{df}{dx}
\frac{d}{dx}f(g(x)) = g^{'}(x)f^{'}(g(x))
\frac{d}{dx}k\cdot f(x) = k\cdot \frac{d}{dx}f(x)
同學~
微積分對我來說就是九九乘法表

積分
函數底下的面積*
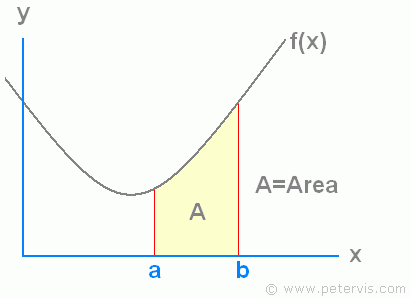
\int_{a}^{b} f(x) dx =
計算
分很多塊加起來?
可以阿

聰明一點呢?
微積分基本定理*
\int_{a}^{b}f(x) = F(b)-F(a) \\
其中\frac{d}{dx}F(x) =f(x)
證明*:
例子
\int_{-\pi}^{\pi}{-x^2}{dx}
\\
\int_{1}^{\infty}{\frac{1}{x}}{dx}
\\\int_{0}^{\infty}{e^{-x}}{dx}
\\
\int_{0}^{\frac{\pi}{2}}{\sin{(x)}} {dx}
\\
\int {\frac{1}{x^2-1}} dx
\\
\int xe^x dx
多維度函數
就是變數不只一個的函數
f:\reals^n\mapsto \reals^m
多維函數的微分
f(x,y,z,w,k,n,g,m,orz)
哪一個?
指定要那一個變數:偏微分
\frac{\partial f}{\partial x}
其他的變數當常數看
why?
例子
f(x,y,z) = \sin(2x+y^2)e^z\\
f(x,y,z) = \begin{bmatrix}x^2y\\ln(z+x)\end{bmatrix}
\\
\frac{\partial f}{\partial x} = ?\\\\
\frac{\partial f}{\partial y} = ?\\\\
\frac{\partial f}{\partial z} = ?\\\\
多維度的積分
一個多維空間是不是有更多可以積的東西
點?線?面?體?更高維度的空間?

在線上積分(線積分)
\int_c f
在面積分(曲面積分)
\iint_s f

在體上積分
\iiint_{v} f

小知識
what is this?
\oint \oiint \oiiint
富比尼定理*
\int_{a_1}^{b_1} \int_{a_2}^{b_2} f(x,y)\,dx\,dy =\int_{a_2}^{b_2} \int_{a_1}^{b_1} f(x,y)\,dy\,dx
梯度 旋度 散度
向量場和純量場
場?
其實只是一個函數
回想之前的定義
F:\reals^n\mapsto \reals^m
純量場: m = 1
向量場: m>=2
直觀上來說

梯度
從一個純量場變成一個向量
F:\reals^n \mapsto \reals 的話,產生n維向量
\begin{bmatrix}
\frac{\partial f}{ \partial x}\\\\
\frac{\partial f}{ \partial y}\\\\
\frac{\partial f}{ \partial z}\\
\end{bmatrix}
意義


指向最大值的方向
散度
向量場上一個點發散的程度
\frac{\partial f_x}{\partial x}+\frac{\partial f_y}{\partial y}+\frac{\partial f_z}{\partial z}
看圖

旋度
向量場上旋轉的程度
(用一向量表示)
\begin{bmatrix}{\frac {\partial F_{z}}{\partial y}}-{\frac {\partial F_{y}}{\partial z}}\\\\{\frac {\partial F_{x}}{\partial z}}-{\frac {\partial F_{z}}{\partial x}}\\\\{\frac {\partial F_{y}}{\partial x}}-{\frac {\partial F_{x}}{\partial y}}\end{bmatrix}
圖片上

統合
Nabla算子
\nabla = \begin{bmatrix}
\frac{\partial}{\partial x}\\
\frac{\partial}{\partial y}\\\frac{\partial}{\partial z}
\end{bmatrix}

一些酷酷的級數和轉換
Taylor Series
把一個函數用多項式表示
怎麼作
微分
f(x) = a_0x^0+a_1x^1+a_2x^2...
f(x) = \sum\limits_{n=0}^{\infty}{\frac{f^{(n)}(a)}{n!}}(x-a)^n
一些名詞
- 可微性 連續性
- 解析函數
複數拓展
Fourier series
&
Fourier Transfrom
用sin 和cos表示一個函數
怎麼作
積分
f(x) = a_0+a_1cos(1x)+a_2cos(2x).... + b_1sin(1x)
f(x)={\frac {a_{0}}2}+\sum \limits_{n=1}^{\infty }\left[a_{n}\cos \left(nx\right)+b_{n}\sin \left(nx\right)\right]
a_{n}={\frac {1}{\pi}}\int\limits_{-\pi}^{\pi}f(x)\cos(nx)\,dx \\
b_{n}={\frac {1}{\pi}}\int\limits_{-\pi}^{\pi}f(x)\sin(nx)\,dx
連續版的
\hat{f}(\xi) = \int\limits_{-\infty}^{\infty} f(x)e^{i2\pi x\xi} \,dx

應該講不到的
- 拉普拉斯轉換
- z轉換
FFT