cog sci 131 section

week 04/18/22

by yuan meng

agenda

  • weber's w (piantadosi, 2016)
  • implement metropolis-hastings
  • hw9 prompt walkthrough

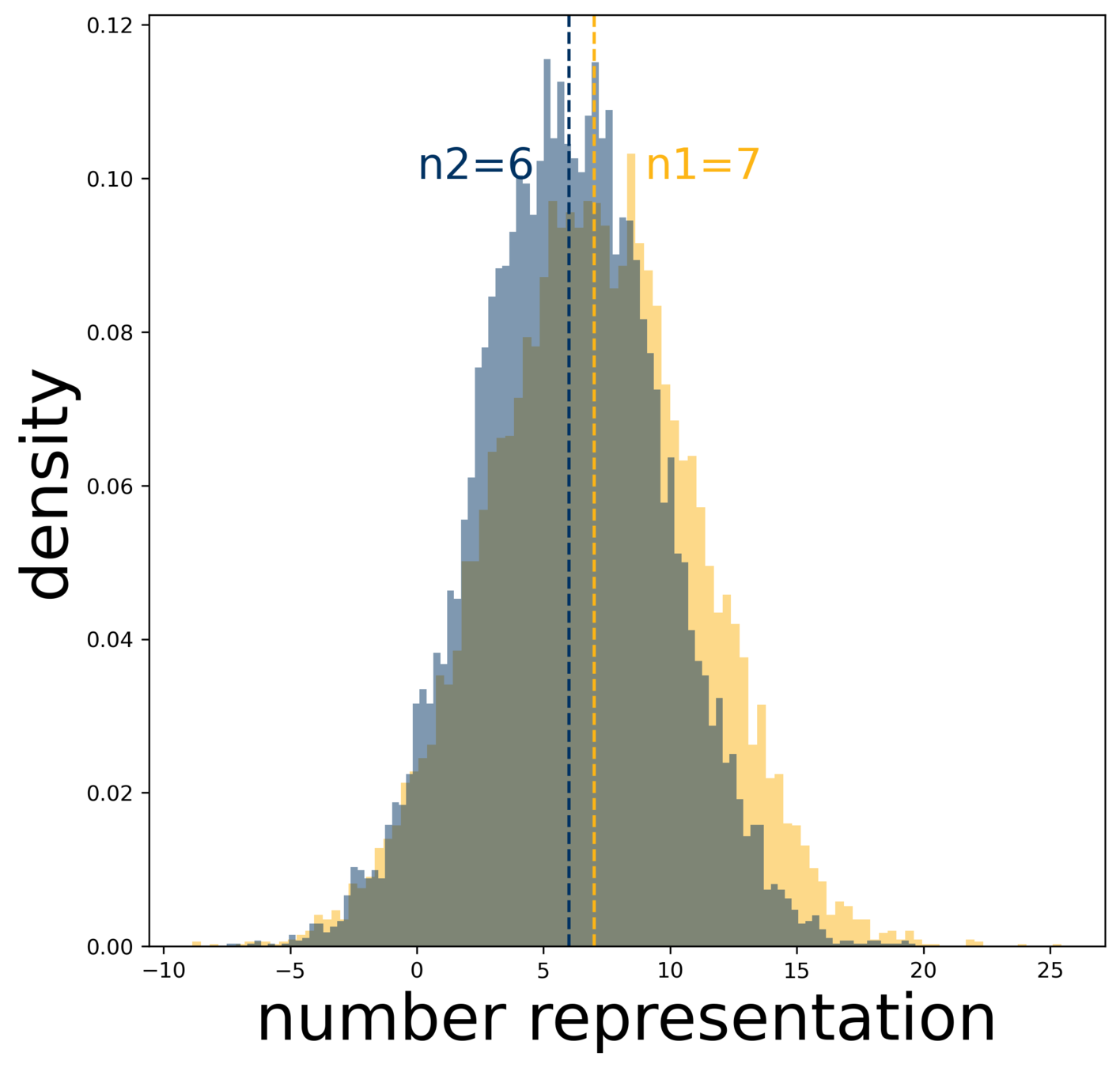
weber ratio W

measures the acuity of the approximate number system (ans)

  • a large number n is represented as a normal distribution centered at n

 

  • the probability that we say n1 ≥ n2 when it's indeed the case is a function of n1, n2, and W

two packs of extremely dangerous dogs 👉 which pack has more?

\mathcal{N}(n,\, W\cdot n)
P(\mathrm{correct}|W, n_1, n_2) = \Phi \left[ \frac{ |n_1 - n_2| } { W \cdot \sqrt{n_1^2 + n_2^2} } \right]

probability of getting it right 👉 this small area

weber ratio W

infer W from response data 

  • prior of W (prior is 0 if W < 0):

 

  • likelihood given k data points:

 

 

  • unstandardized posterior of W:

 

P(W) = e^{-W}
\displaystyle{P(a|W,n_1, n_2) = \prod_{i}^{k} P(a_i|W, n_{1i}, n_{2i})}
\displaystyle{P(W|a, n_1, n_2) = P(W) \cdot \prod_{i}^{k} P(a_i|W, n_{1i}, n_{2i})}
\displaystyle{\log P(W|a, n_1, n_2) = \log P(W) + \sum_{i}^{k} \log P(a_i|W, n_{1i}, n_{2i})}

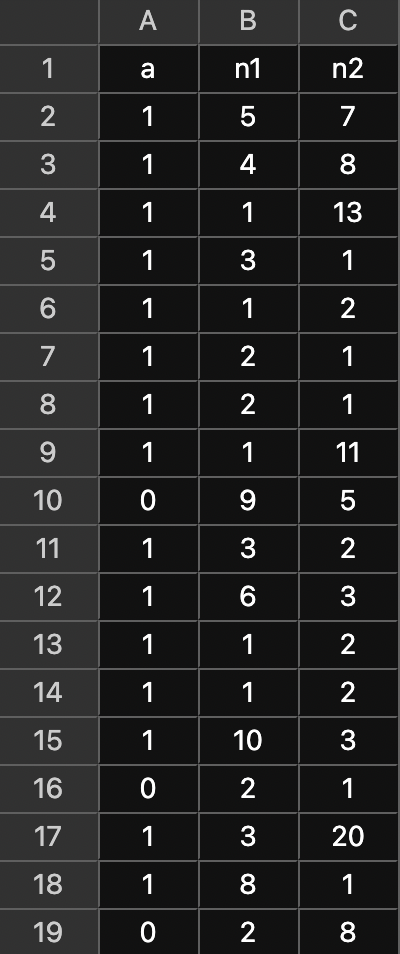
data:

  • each trial is a judgment (do you think n1 > n2?);
  • a = 1: answered correctly; a = 0: answered incorrectly

be sure to take log!

implement metropolis-hastings

  • goal: collect representative samples from the posterior distribution of W
  • the sampling algorithm
    1. initialize: pick a random W
    2. propose: W' = W + noise
    3. decide whether to accept W'
      • ​​​if P(W'|D) > P(W|D), definitely accept
      • even if P(W'|D) ≤ P(W|D), accept W' with a P(W'|D)/P(W|D) probability
    4. iterate over 1-3, each time starting with the last accepted W
  • sampling vs. optimization: a sampler doesn't alter the value of W, but an optimizer (e.g., gradient descent) does
  • burn-in: people usually discard the first bunch of samples which may not be good
def metropolis_hastings(n1, n2, a, n_iters):
    # generate a random W 
    W = # sample a value from some distribution
   
    # log posterior of initial W
    log_p = log_posterior(n1, n2, a, W)
    # arrays to collect samples and log posteriors
    Ws, log_ps = np.zeros(n_iters), np.zeros(n_iters)

    # collect samples from posterior
    for iter in range(n_iters):
        # propose a new W
        W_new = # add a noise from Normal(0, 0.1)
        # calculate new log posterior
        log_p_new = log_posterior(n1, n2, a, W_new)
        # log ratio of new and old log posteriors
        log_ratio = # what should this be?
        # decide whether to accept W_new
        if # write your own condition:
            W = W_new
            log_post = log_post_new

        # collect sample from this iteration
        Ws[iter], log_ps[iter] = W, log_post

    # return samples
    return {"W": Ws, "log_posteriors": log_ps}

most challenging bit

  1. need to adapt original criteria to log-transformation
  2. if cleverly written, can use one simple if-statement to catch both acceptance conditions

(ofc, critical parts commented out)

hw9 prompts

samples from posterior

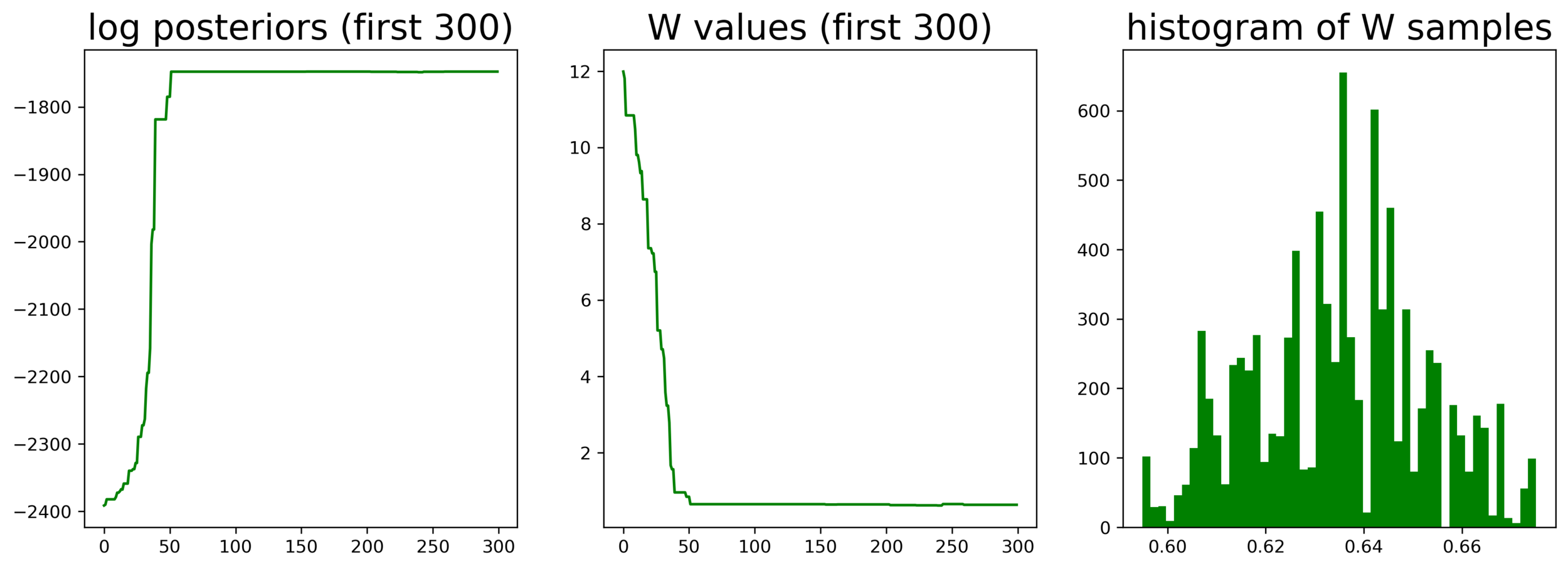
homework 9, q5

samples from prior

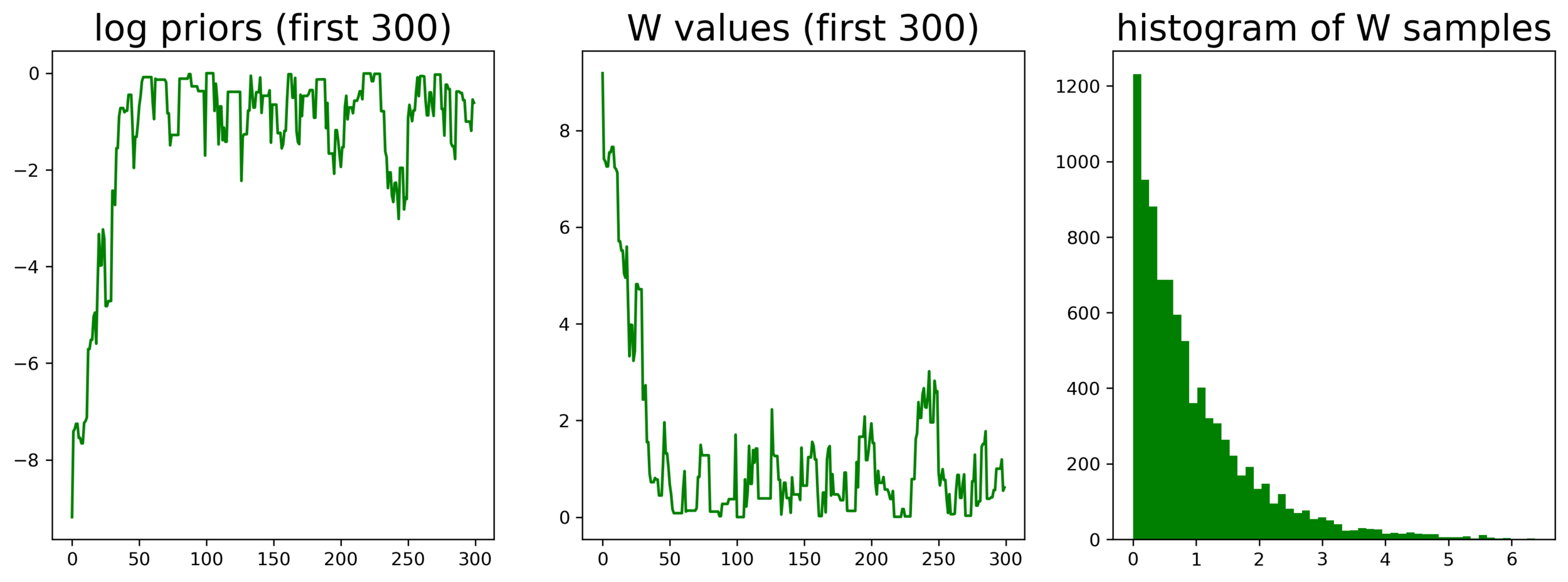
homework 9, q7

bayesian cognitive model

vs. bayesian data analysis 

bayes as a model of cognition: a normative model that dictates what an ideal learner should do given data and prior 

bayes as a data analysis tool: a descriptive model that captures what a real learner did do given data and prior

the same prior and data lead to the same inference 👉 if prior is optimal, then inference is optimal

e.g., seeing 100 heads in a row, the probability that the tosser is a psychic? 

different people may discount observations differently 👉 can learn each person's "discount rate" from data

tauber et al. (2017)