微分方程式の数値解析 と データサイエンス
宮武 勇登 (大阪大学)

京都大学理学部数学特別講義(応用数学 II)
自己紹介
略歴
2018 -
大阪大学サイバーメディアセンター
准教授
2015 - 2017
名古屋大学工学研究科 助教
2015
日本応用数理学会・日本数学会・SIAM
(理学部数学科・情報科学研究科情報基礎数学専攻)
所属学会
- 微分方程式の 数値解析
- 数値線形代数
- 数値計算の不確実性定量化
- 地震分野などとの協働
応用数学の一分野としての 数値解析 とは
問題を数値的に解析するための
- アルゴリズムの開発,および
- その数学解析
連立一次方程式や行列関数など
行列に関連する計算アルゴリズムの研究
応用数学の一分野としての 数値解析 とは
博士 (情報理工学) 東京大学
集中講義のスケジュール等の情報
月 15:00 - 17:00
火 15:00 - 17:00
水 10:00 - 12:00
木 15:00 - 16:45
金 10:00 - 12:00
オーバービュー,モデル縮減
動的低ランク近似
最適化
アジョイント法
計算の不確実性定量化
(今日の後半〜アジョイント法は板書の予定)
講義ノート,レポート課題(木曜日に出題予定):
微分方程式
時空間に 連続的 に変化する現象のモデル方程式
ニュートンの運動方程式
ナビエ・ストークス方程式
\( \displaystyle m\frac{\mathrm d^2 \bm{r}}{\mathrm d t^2} =F\)
\( \displaystyle \frac{\partial \bm{v}}{\partial t} + (\bm{v}\cdot \nabla)\bm{v} = -\frac{1}{\rho}\nabla p + \nu \nabla^2 \bm{v} + \bm{g}\)
時間連続な現象のモデル
時空間連続な現象のモデル
常微分方程式
ODE (ordinary differential equation)
偏微分方程式
PDE (partial differential equation)
通常は 物理的な現象 や 経済 のモデル
微分方程式 と データサイエンス
行列
ODE Net

(Chen et al. 2018)
動的低ランク近似
最適化

画像処理

?
集中講義でお伝えしたいこと
- 近年,データサイエンスにおいて微分方程式が活用されている
- 最終的には,離散化して数値計算することがほとんど
- 数値解析の入門書に書いてある手法では多くの場合不十分
- データサイエンスの応用を意識した新しい数値解析
数値解析の入門書に書いてある内容
とはいえ,まずは...
超ダイジェスト版!!
常微分方程式の数値計算とは
基本的には 離散変数法
\( \displaystyle \frac{\mathrm d}{\mathrm dt} \bm{u}(t) = \bm{f} (\bm{u}(t)), \quad \bm{u}(0)=\bm{u}_0 \in \mathbb{R}^d\)
離散時刻 \(t=t_1,t_2,\dots\) 上の近似解を求める
(刻み幅が等間隔ならば \(t_n=nh\))
\(\bm{u}_1\approx \bm{u}(t_1)\)
\(\bm{u}_2\approx \bm{u}(t_2)\)
\(\vdots\)

time
刻み幅:\(h\) or \(\Delta t\)
常微分方程式の数値解法の分類
離散変数法の代表的解法
一段解法
多値法
\(\bm{u}_n\) から \(\bm{u}_{n+1}\) を計算
\(\bm{u}_{n-k},\dots,\bm{u}_n\) から \(\bm{u}_{n+1}\) を計算
- Runge–Kutta法
- 分離型Runge–Kutta法
- splitting法 など
- 線形多段階法
- 一般線形法 など
- Runge–Kutta法
注意:公式を表すとき
\(\bm{u}_n\mapsto\bm{u}_{n+1}\) で表現したり
\(\bm{u}_0\mapsto \bm{u}_1\) で表現したりします
Euler法(オイラー法)
\( \displaystyle \frac{\bm{u}_{n+1}-\bm{u}_n}{h} = \bm{f}(\bm{u}_n)\)
\( \displaystyle \frac{\mathrm d}{\mathrm dt} \bm{u}(t) = \bm{f} (\bm{u}(t)), \quad \bm{u}(0)=\bm{u}_0 \in \mathbb{R}^d\)
\( \displaystyle \lim_{h\to 0}\frac{\bm{u}(t_n+h)-\bm{u}(t_n)}{h} = \bm{f}(\bm{u}(t_n))\)
\( \displaystyle \frac{\bm{u}(t_n+h)-\bm{u}(t_n)}{h} \approx \bm{f}(\bm{u}(t_n))\)
微分を近似
「微分を近似する」という考え方はシンプルだけど、
この視点でできることは限られる
積分の近似
\(0\)
\(h\)
\( \displaystyle \frac{\mathrm d}{\mathrm dt} \bm{u}(t) = \bm{f} (\bm{u}(t)), \quad \bm{u}(0)=\bm{u}_0 \in \mathbb{R}^d\)
\( \displaystyle \bm{u}(t_n+h) = \bm{u}(t_n) + \int_0^h \bm{f}(\bm{u}(t_n + s))\,\mathrm ds\)
\( \displaystyle \approx \bm{u}(t_n) + h \bm{f}(\bm{u}(t_n ))\)
\( \displaystyle \bm{u}_{n+1}= \bm{u}_n + h \bm{f}(\bm{u}_n)\)

\( \bm{f}(\bm{u}(t_n +s)) \)
\(s\)
厳密解の積分表現
積分を近似
右辺ベクトルの近似

\(\bm{u}(t)\)
\(\bm{f}(\bm{u}_0)\)
\(\bm{u}(0)=\bm{u}_0\)
Euler法の数値解
傾きの平均をとってみる
\(\bm{u}(t)\)
\(\bm{k}_1=\bm{f}(\bm{u}_0)\)
\(\bm{u}(0)=\bm{u}_0\)
Heun法の数値解
\(\bm{k}_2=\bm{f}(\bm{u}_{\text{Euler}})\)

\(\displaystyle \frac{\bm{k}_1+\bm{k}_2}{2}\)
(注意) Heun(ホイン)法は Heun ではなく Runge が発見した公式 (1895)
(Improved Euler法と呼ばれることも)
(入門書に載っている)Runge–Kutta法
4段4次の陽的RK法
\(\bm{k}_1 =\bm{f}(\bm{u}_0) \)
\(\bm{k}_2 =\bm{f}(\bm{u}_0+\frac{h}{2}\bm{k}_1) \)
\(\bm{k}_3 =\bm{f}(\bm{u}_0+\frac{h}{2}\bm{k}_2) \)
\(\bm{k}_4 =\bm{f}(\bm{u}_0+h\bm{k}_3) \)
\(\bm{u}_1 = \bm{u}_0 + h \big( \frac{1}{6}\bm{k}_1 + \frac{2}{6}\bm{k}_2 + \frac{2}{6}\bm{k}_3 + \frac{1}{6}\bm{k}_4 \big) \)
Butcher配列
(こんなふうに表現することも)

- Kuttaは右の公式も発見している
- 実はこの公式の方が誤差は小さいが、
上の公式の方が覚えやすいため広く利用されている
(注意)
発見したのはKutta (1901)
Runge–Kutta法
\( \displaystyle \frac{\mathrm d}{\mathrm dt} \bm{u}(t) = \bm{f} (\bm{u}(t),t), \quad \bm{u}(0)=\bm{u}_0 \in \mathbb{R}^d\) に対する一般の \(s\) 段 RK法
\(\displaystyle \bm{k}_i =\bm{f}\big(\bm{u}_n+h\sum_{j=1}^s a_{ij} \bm{k}_j,t_n + c_j h\big) \) (\(i=1,\dots,s\))
\(\displaystyle \bm{u}_{n+1} = \bm{u}_n + h \sum_{i=1}^s b_i \bm{k}_i \)
Butcher配列

\(A\) が「下三角行列(対角は 0 )」ならば陽解法 → 陽的RK法
有名な公式
陽的Euler法
Rungeの公式
Rungeの公式
陰的Euler法
中点則
Gauss公式
陽解法
陰解法
数値解法の精度
常微分方程式の数値解法の精度
以下のように評価できる数値解法を 「\({\color{magenta}p}\) 次精度解法」 と呼ぶ
\(\|\bm{u}(h)-\bm{u}_1\|= \mathrm{O}(h^{{\color{magenta}p}+1})\)
これは 1ステップ毎 に混入する「局所誤差」
大域誤差は...
とてもラフに議論すれば、目標時刻を \(T\) としたとき、
\(t_N = T(=Nh)\) における大域誤差は
\(Ch^{p+1}\times N = CNhh^p = CTh^p = \mathrm{O}(h^{\color{magenta}p})\)
次数が異なると...
- 次数 と 傾き がほぼ同じ
- 誤差の小さい数値解を得るためには
次数の高い解法の方が効率的なことが多い - 刻み幅を変えると誤差が今と比べて
相対的にどう変わるか予想できる - テスト問題を除いて,実際の誤差の大きさは
よく分からないことが多い
異なる刻み幅で計算したときの大域誤差

陽的RK法で \(p\) 次精度を達成する最小段数
- \(p=1\) : 陽的Euler法
- \(p=2\) : Runge (1895)
- \(p=3\) : Heun (1900)
- \(p=4,5\) : Kutta (1901)
ただし、\(5\) 次精度解法にはミスあり
Nyström (1925) で修正
\(5\) 段 \(5\) 次が可能かどうかは当時不明
→ 不可能 by Butcher (1963頃)
最小段数
\(p\)
\(1\)
\(1\)
\(2\)
\(2\)
\(3\)
\(3\)
\(4\)
\(4\)
\(5\)
\(6\)
\(6\)
\(7\)
\(7\)
\(9\)
\(8\)
\(11\)
\(\cdots\)
\(\cdots\)
\(10\)
\(17\)
- \(p=6\) : Butcher (1964)
- \(p=7\) : \(8\) 段では不可能 by Butcher (1965)
\(9\) 段公式は複数の研究者が1968年頃発見 - \(p=8\) : Curtis (1970)
\(10\) 段では不可能 by Butcher (1985) - \(p=10\) : Hairer (1978) ← ギネス記録
2019年に,\(16\) 段で可能という報告あり
陰的RK法は \(s\) 段 \(2s\) 次 が可能

数値解法の安定性
安定性の評価基準はたくさんあるが、最も基本的なものを紹介
安定性の評価基準はたくさんあるが、最も基本的なものを紹介
(複素数値のスカラーODE)
テスト方程式
\( \displaystyle \frac{\mathrm d}{\mathrm dt} u(t) = \lambda u(t),\)
\( \displaystyle u(0) = u_0 \in \mathbb{C}\)
\( \lambda\) は複素数で、その実部は 負 とする
解は \( \displaystyle u(t) = \mathrm{e}^{\lambda t} u_0 \) なので、\( |u(t)| = |\mathrm{e}^{\lambda t}u_0|<|u_0|\) \((t>0)\) が成り立つが、
RK法による近似解に対してもこの性質は成り立つだろうか?
Euler法の場合
\(u_1 = (1+h\lambda)u_0\) より \(|u_1|<|u_0|\) となるには
陽的Euler法
陰的Euler法
\(|1+h\lambda|<1\)
\(u_1 = u_0 + h\lambda u_1\) より \(\displaystyle u_1 = \frac{1}{1-h\lambda}u_0\)
\(h>0\) ならば必ず \(|u_1|<|u_0|\)
無条件に安定
\(h\) が大きいとこの不等式は成り立たない


Runge–Kutta法の場合
RK法の時間発展の一表現
\(u_1 = \underbrace{R(z)}_{}u_0\) (\(z=h\lambda\))
\(\displaystyle R(z) = \frac{\mathrm{det}(I-zA + z\bm{e}\bm{b}^\top)}{\mathrm{det}(I-zA)}\) \((\bm{e}=[1,\dots,1]^\top)\)
RK法の安定性因子
A安定性
- 安定性領域: \(\mathcal{R} := \{z\in\mathbb{C} \mid |R(z)|<1\}\)
- \(\mathcal{R} \supset \mathbb{C}^{-} =\{z\in\mathbb{C} \mid \mathrm{Re}(z)<0\}\) を満たすRK法を
「A安定」な解法という
(\(\mathbb{C}^{-}\):複素平面の左半分)
陽的Runge–Kutta法の安定性領域
- \(p\) 段 \(p \) 次の陽的RK法の安定性領域は同一
(例:4段4次の陽的RK法は複数存在するが、
その安定性領域はどれも同じ) - \(p=5\) (6段) の図は一例
- どれも \(\mathbb{C}^{-}\) (=左半平面) からは程遠い
\(\lambda\) の実部が負の方に大きいと
\(h\) はものすごく小さくとらないといけない - Gauss–Runge–Kutta法 (陰的RK法) は A安定

硬い系(stiffness)
硬い系
陽的RK法で計算する場合に、
刻み幅を極めて小さくとらないと、数値的に不安定になってしまう系
RK法の場合
- 陰解法を用いる
- 安定性領域ができる限り実軸の左の方を覆うように設計された
RK法を用いる
例題
\( \displaystyle \frac{\mathrm d}{\mathrm dt} \bm{u}(t) = \begin{bmatrix} -1& 1\\2 & -3\end{bmatrix} \bm{u}(t) + \begin{bmatrix}\cos t \\ 3\cos t - \sin t \end{bmatrix} ,\quad \bm{u}(0) = \begin{bmatrix} 1\\ 2\end{bmatrix}\)
例 1
\( \displaystyle \frac{\mathrm d}{\mathrm dt} \bm{u}(t) = \begin{bmatrix} -2& 1\\1998 & -1999\end{bmatrix} \bm{u}(t) + \begin{bmatrix}-\cos t \\ 1999\cos t - \sin t \end{bmatrix} ,\quad \bm{u}(0) = \begin{bmatrix} 1\\ 2\end{bmatrix}\)
例 2
実はどちらも厳密解は \( \displaystyle \bm{u}(t) = \mathrm{e}^{-t} \begin{bmatrix} 1 \\ 1\end{bmatrix} + \begin{bmatrix}0 \\ \cos t\end{bmatrix}\)
微分方程式もなんとなく似通っているし、
RK法で計算した近似解も似ているはず...?
(「三井, 常微分方程式の数値解法」 の例)
陽的Runge–Kutta法 と 中点則
4段4次の陽的RK法


中点則(陰解法)
例 1
例 2
例 1 と 例 2 はほとんど同じ
(刻み幅はどちらも \(h=0.01\))
例 2 は 2 ステップ目 で発散...
違いは何か?
固有値:\(-1, -4\)
\( \displaystyle \frac{\mathrm d}{\mathrm dt} \bm{u}(t) = \underbrace{\begin{bmatrix} -1& 1\\2 & -3\end{bmatrix}}_{} \bm{u}(t) + \begin{bmatrix}\cos t \\ 3\cos t - \sin t \end{bmatrix} \)
例 1
\( \displaystyle \frac{\mathrm d}{\mathrm dt} \bm{u}(t) = \underbrace{\begin{bmatrix} -2& 1\\1998 & -1999\end{bmatrix}}_{} \bm{u}(t) + \begin{bmatrix}-\cos t \\ 1999\cos t - \sin t \end{bmatrix} \)
例 2
固有値:\(-1, -2000\)

だいたい、\(-3 < -4h \, (h<3/4)\) くらいで安定に計算できる!

- RK法を使うなら \(h<3/2000\) くらい小さくとらないといけない
- 中点則なら特に制限なし (ただし精度の問題はある)
改めて「硬い系」とは?
- 行列 \(A\) について絶対値が大きな固有値を持つ問題は
「硬い系」になる - 硬度比が大きな問題も「硬い系」になりうる
- 硬度比が大きくても硬い系ではないかもしれないが、
初期値の変動に対しては不安定
線形系:\( \displaystyle \frac{\mathrm d}{\mathrm dt}\bm{u}(t) = A\bm{u}(t) + \bm{\phi}(t) \) に対して...
硬度比 \(\displaystyle =\)
| \(A\) の絶対値最大固有値 |
| \(A\) の絶対値最小固有値 |
例 2 は「硬い系」とまでは言えず、「硬い系に近い」という程度の問題
(注) 非線形問題の場合は、線形化してあらわれるJacobi行列の固有値に着目する
硬い系に対する数値解法
安定性領域が、(特に左方向に) 広い解法を使う!
- A安定な解法
- 「硬い系専用」の解法
- 陽解法ならば、安定性領域が実軸左方向に広がっている解法

(引用:Hairer, Wanner, Solving Ordinary Differential Equations II, 1996)
数値解析の入門書に書いてない現代的な内容
Störmer法
Newtonの運動方程式: \(\displaystyle \frac{\mathrm d^2}{\mathrm dt^2} \bm{q} = -\nabla V(\bm{q}) \) \(\Leftrightarrow\) \(\displaystyle \frac{\mathrm d}{\mathrm dt} \begin{bmatrix} \bm{q} \\ \bm{p} \end{bmatrix} = \begin{bmatrix} \bm{p} \\ -\nabla V(\bm{q}) \end{bmatrix}\)
Störmer法 (1907)
\( \displaystyle \bm{q}_{n+1/2} = \bm{q}_n + \frac{h}{2}\bm{p}_n\)
\( \displaystyle \bm{p}_{n+1} = \bm{p}_n - h \nabla V(\bm{q}_{n+1/2})\)
\( \displaystyle \bm{q}_{n+1} = \bm{q}_{n+1/2} + \frac{h}{2}\bm{p}_{n+1}\)
- Verlet法 (1967; 分子動力学) も本質的に同じ
- 数値解析学者は Störmer–Verlet法 と呼んだりする
あるいは、Newton–Störmer–Verlet法
位置 \(\bm{q}\) を陽的Euler法で半ステップ更新
運動量 \(\bm{p}\) を1ステップ更新
位置 \(\bm{q}\) を残りの半ステップ更新

Keplerの二体問題の数値計算
約1周期分の計算

約10周期分の計算
計算する時間が長くなるとStörmer法が有利

エネルギー保存則

太陽系のシミュレーション
陽的Euler法

陰的Euler法
Störmer法
Symplectic Euler法
Störmer法の
親戚(こども)解法
Störmer–Verlet法はなぜ優れている?
Newtonの運動方程式は Hamilton系
→ 解の時間発展写像は シンプレクティック (symplectic)

SV法による近似解の離散的な時間発展写像もシンプレクティック
→ もとの系に非常によく似たHamilton系を厳密に解いている
\(\mathbb{R}^2\) の場合:
シンプレクティック性 = 位相空間内の面積保存性
(引用:Hairer, Lubich, Wanner, Geometric Numerical Integration, 2006)
幾何学的数値積分法 ・ 構造保存数値解法
(Geometric Numerical Integration)
(Structure-preserving numerical methods)
問題 (微分方程式) の数理構造を離散化後も厳密に再現する数値解法
- シンプレクティック解法
- エネルギー保存解法 (シンプレクティック解法とは両立しない)
- エネルギー散逸解法
- 多様体上の微分方程式に対する数値解法
- 高振動系やマルチスケール問題に対する数値解法
研究者の主なタスク
- どのように構造保存アルゴリズムを設計すればよいか?
- 恩恵は何か?
Störmer法はシンプレクティックだが、さらに...
Keplerの第2法則 (角運動量保存則)
双線形形式の保存!
実は Störmer法 を含む「分離型Runge–Kutta法」という解法クラスに対して
Hamilton系に対してシンプレクティック \(\Leftrightarrow\) 任意の双線形形式を保存 \({}^\ast\)
\(\displaystyle \frac{\mathrm d}{\mathrm dt} \begin{bmatrix} \bm{q} \\ \bm{p} \end{bmatrix} = \begin{bmatrix} \bm{p} \\ -\nabla V(\bm{q}) \end{bmatrix}\), \(\displaystyle V(\bm{q}) = \frac{1}{q_1^2 + q_2^2} \)
\(q_1 p_2 - q_2 p_1=\text{const.}\)
(\({}^\ast\) 双線形形式の保存量があるとき自動的に保存性を再現)
なお、RK法に関しては
Hamilton系に対してシンプレクティック \(\Leftrightarrow\) 任意の2次の保存量を保存
ODE Net の誤差逆伝播法
問題設定
\(\displaystyle \frac{\mathrm d}{\mathrm dt} \bm{u} = \bm{f} (\bm{u},t,\bm{\theta})\), \(\bm{u}(0)=\bm{u}_0\)

Loss: \(\displaystyle \mathcal{L}(\bm{u}(T;\bm{\theta})) \)
小さくしたい
現実には... \( \mathcal{L}(\bm{u}_N (\bm{\theta}))\) を小さくしたい

\(\displaystyle \nabla_{\bm{\theta}}\mathcal{L}(\bm{u}(T;\bm{\theta})) \) や \(\displaystyle \nabla_{\bm{\theta}}\mathcal{L}(\bm{u}_N(\bm{\theta})) \) の計算が重要!
(注意) \(\mathcal{L}\) の具体形などを限定しなければ、
データ同化 (特に4次元変分法) と本質的に同じ設定
特にこれが問題
連続の場合:アジョイント (随伴) 法
\(\dot{\bm{\lambda}} = -\big(\nabla_{\bm{u}} \bm{f}(\bm{u})\big)^\top \bm{\lambda}\)
\(\displaystyle \dot{\bm{u}} = \bm{f} (\bm{u})\), \(\bm{u}(0)=\bm{\theta}\)
対象の方程式 :
アジョイント方程式 :
\(\displaystyle \nabla_{\bm{\theta}}\mathcal{L}(\bm{u}(T;\bm{\theta})) \) の評価
\(\displaystyle \bm{\lambda}(T)=\nabla_{\bm{u}}\mathcal{L}(\bm{u}(T;\bm{\theta})) \) を満たす解 \(\bm{\lambda}(t)\) に対して \(\displaystyle \bm{\lambda}(0)=\nabla_{\bm{\theta}}\mathcal{L}(\bm{u}(T;\bm{\theta})) \)
簡単のため初期値を \(\bm{\theta}\) とする
アジョイント方程式は時間逆向きに解く!
上の方程式の解
変分方程式を用いた証明
\(\dot{\bm{\lambda}} = -\big(\nabla_{\bm{u}} \bm{f}(\bm{u})\big)^\top \bm{\lambda}\)
\(\displaystyle \dot{\bm{u}} = \bm{f} (\bm{u})\), \(\bm{u}(0)=\bm{\theta}\)
対象の方程式 :
アジョイント方程式 :
\(\dot{\bm{\delta}} = \big(\nabla_{\bm{u}} \bm{f}(\bm{u})\big) \bm{\delta}\)
変分方程式 :
補題 : \(\displaystyle \frac{\mathrm d}{\mathrm dt} \big( \bm{\lambda}^\top \bm{\delta}\big) = 0\)
双線形形式の保存!
\(\displaystyle \because \frac{\mathrm d}{\mathrm dt} \big( \bm{\lambda}^\top \bm{\delta}\big) =\dot{\bm{\lambda}}^\top \bm{\delta} + \bm{\lambda}^\top \dot{\bm{\delta}}= 0\)
特に \(\bm{\lambda}(T)^\top \bm{\delta}(T)=\bm{\lambda}(0)^\top \bm{\delta}(0)\)
連鎖律 \(\displaystyle \nabla_{\bm{\theta}}\mathcal{L}(\bm{u}(T;\bm{\theta})) = (\nabla_{\bm{\theta}}\bm{u}(T;\bm{\theta}))^\top \nabla_{\bm{u}}\mathcal{L}(\bm{u}(T;\bm{\theta})) \) と
変分方程式の性質 \(\displaystyle \bm{\delta}(T)= (\nabla_{\bm{\theta}}\bm{u}(T;\bm{\theta})) \bm{\delta}(0) \) より
\(\displaystyle \big(\nabla_{\bm{u}}\mathcal{L}(\bm{u}(T;\bm{\theta})))^\top \bm{\delta}(T) = \big(\nabla_{\bm{\theta}}\mathcal{L}(\bm{u}(T;\bm{\theta})))^\top \bm{\delta}(0)\)
(\(\ast\))
(\(\ast\)) と比べると、\(\displaystyle \bm{\lambda}(T)=\nabla_{\bm{u}}\mathcal{L}(\bm{u}(T;\bm{\theta})) \) を満たす解 \(\bm{\lambda}(t)\) に対して \(\displaystyle \bm{\lambda}(0)=\nabla_{\bm{\theta}}\mathcal{L}(\bm{u}(T;\bm{\theta})) \)

双線形形式の保存!
離散の場合
\(\displaystyle \dot{\bm{u}} = \bm{f} (\bm{u})\), \(\bm{u}(0)=\bm{\theta}\)
対象の方程式 :
\(\displaystyle \nabla_{\bm{\theta}}\mathcal{L}(\bm{u}_N(\bm{\theta})) \) の評価
近似計算して \(\bm{u}_N(\bm{\theta}) \approx \bm{u}(T;\bm{\theta})\)
\(\dot{\bm{\lambda}} = -\big(\nabla_{\bm{u}} \bm{f}(\bm{u})\big)^\top \bm{\lambda}\)
アジョイント方程式 :
\(\dot{\bm{\delta}} = \big(\nabla_{\bm{u}} \bm{f}(\bm{u})\big) \bm{\delta}\)
変分方程式 :
近似計算して \(\bm{u}_N(\bm{\theta}) \approx \bm{u}(T;\bm{\theta})\)
対象の方程式と同じ手法で離散化
(実際に計算する必要はない)
\(\bm{\lambda}_n^\top \bm{\delta}_n =\text{const.}\) となるように離散化
双線形形式の保存!
終端条件 \(\displaystyle \bm{\lambda}_N=\nabla_{\bm{u}}\mathcal{L}(\bm{u}_N(\bm{\theta})) \) を課し、時間逆向きに計算すると \(\displaystyle \bm{\lambda}_0=\nabla_{\bm{\theta}}\mathcal{L}(\bm{u}_N(\bm{\theta})) \)
アジョイント方程式の離散化 (RK法の場合)
\(\dot{\bm{\lambda}} = -\big(\nabla_{\bm{u}} \bm{f}(\bm{u})\big)^\top \bm{\lambda}\)
\(\displaystyle \dot{\bm{u}} = \bm{f} (\bm{u})\), \(\bm{u}(0)=\bm{\theta}\)
対象の方程式 :
アジョイント方程式 :
\(\dot{\bm{\delta}} = \big(\nabla_{\bm{u}} \bm{f}(\bm{u})\big) \bm{\delta}\)
変分方程式 :
「対象の方程式」と「変分方程式」を \(s\) 段RK法 \((A,\bm{b},\bm{c})\) で離散化した場合
「アジョイント方程式」は \(s\) 段RK法 \((\widehat{A},\widehat{\bm{b}},\widehat{\bm{c}})\) で離散化すればよい
ただし、
\(b_i \widehat{a}_{ij} + \widehat{b}_ja_{ji} = b_i \widehat{b}_j,\)
\(i,j=1,\dots,s\)
\(\widehat{b}_i=b_i,\) \(\widehat{c}_i = c_i,\)
\(i=1,\dots,s\)
- 分離型RK法が双線形形式の保存量を自動的に再現する条件
- Newton–Störmer–Verlet法は一例
Newton–Störmer–Verlet法 再考
分離型ODE系
に対する 分離型RK法
\(\displaystyle \bm{k}_i = \bm{f}\big(\bm{y}_0 + h\sum_{j=1}^s a_{ij}\bm{k}_j, \bm{z}_0 + h\sum_{j=1}^s \widehat{a}_{ij} \bm{l}_j\big) \)
\(\displaystyle \bm{l}_i = \bm{g}\big(\bm{y}_0 + h\sum_{j=1}^s a_{ij}\bm{k}_j, \bm{z}_0 + h\sum_{j=1}^s \widehat{a}_{ij} \bm{l}_j\big) \)
\(\displaystyle \bm{y}_1 = \bm{y}_0 + h\sum_{i=1}^s b_i \bm{k}_i\)
\(\displaystyle \bm{z}_1 = \bm{y}_0 + h\sum_{i=1}^s \widehat{b}_i \bm{l}_i\)
NSV法の場合
(注意) 一般には陰解法
前頁の条件を満たす
補足 : 2階微分も計算できます!
2階微分 = ヘッシアン \(H\)
\(H \bm{x} = \bm{b}\) のような連立一次方程式を解きたいことがほとんど
- \(H\) は通常、大規模・密行列なので、\(H\) の計算は非現実的
- CG法 (共役勾配法 : Krylov部分空間法の一種) など を用いるなら
「ヘッシアン \(\times\) ベクトル」 の計算ができれば十分
通常のネットワークの場合
動的低ランク近似
行列の低ランク近似
\(A\in\mathbb{R}^{m\times n}\) に対し、ランクが \(k\) 以下の \(m\times n\) 型行列の中で
\(\displaystyle \min_{\text{rank}(X)\leq k}\| X - A\|_{\mathrm{F}}^2\)
フロベニウスノルムの意味で \(A\) との距離が最小になるものを求めよ
(注) \(\displaystyle \|A\|_{\mathrm{F}}^2 := \sum_{i=1}^m \sum_{j=1}^n a_{ij}^2\)

特異値分解で解ける!
特異値分解
ランク \( r\) の実行列 \(A\in\mathbb{R}^{m\times n}\) は
適当な \(m\) 次直交行列 \(V\) と \(n\) 次直交行列 \(U\) と用いて
\(A = U\Sigma V^\top\)
の形に分解される
ここで、\(\Sigma\) は
の形の \(m\times n\) 型行列
\(\sigma_1,\dots,\sigma_r\) : 「特異値」という

左上から大きい順に並んでいるとする
低ランク近似問題の解
\(A=\)
\(U\)
\(\Sigma\)
\(V^\top\)
\(A_k=\)
\(U_k\)
\(\Sigma_k\)
\(V_k^\top\)
最適解!
注意 : \(U_k^\top U_k = V_k^\top V_k = I_k\) (単位行列)
Eckart–Young–Mirskyの定理
最適解 \(=A_k\)
この事実は非常に有名だが、「初等的な証明」を与えている文献は少ない
スペクトルノルム (\(l^2\)ノルム) とフロベニウスノルムの場合に限定して
初等的証明
ユニタリ不変ノルム (フロベニウスノルムも含む) に対して
初等的証明
問題設定
\(A(t)\in\mathbb{R}^{m\times n}\) : 変数 \(t\) に関して連続な行列 に対して
\(\| X(t) - A(t)\|_{\mathrm{F}}\) を最小にする ランク \(k\) 行列 \(X(t)\) を求めよ
あるいは、連続的に変化する行列の列 \(A_1,A_2,\dots\) に対して
\(\| X_i - A_i\|_{\mathrm{F}}\) を最小にする ランク \(k\) 行列 \(X_1,X_2,\dots\) を求めよ
当然、各 \(t\) や 各 \(i\) で低ランク近似したものが最適解だが
それなりに高コスト...
∵ 大規模行列の特異値分解の計算は大変...

問題を近似
\(\mathcal{M}_k\) : ランク \(k\) の \(m\times n\) 行列の集合 (多様体)
\(T_Y \mathcal{M}\) : \(Y\) における \(\mathcal{M}_k\) の接空間
\(\| X(t) - A(t)\|_{\mathrm{F}}\) を最小にする 行列 \(X(t)\in\mathcal{M}_k\) を求めよ
\(\| \dot{Y}(t) - \dot{A}(t)\|_{\mathrm{F}}\) を最小にする 行列 \(\dot{Y}(t) \in T_{Y(t)}\mathcal{M}_k\) を求めよ
- \(Y(t)\) は多様体 \(\mathcal{M}_k\) 上のある種の微分方程式の解
- \(X(0)\) を \(Y(t)\) の初期値とし、
初期値問題としての微分方程式を近似的に解く
準最適性
ある条件のもとで
\(\displaystyle \| Y(t) - X(t)\|_\mathrm{F} \leq C(t) \int_0^t \| X(s) - A(s)\|_\mathrm{F}\,\mathrm ds\)
近似解と最適解の差 \(\leq \) 定数 \(\times\) 最適解の誤差の蓄積
(Koch, Lubich, 2007)
どの程度よく近似するか?
(引用 : Koch, Lubich, 2007)

各時刻で特異値分解したときの誤差
動的低ランク近似の解の誤差
動的低ランク近似と最適近似の差
悪くなさそう!
失敗する例
\(\displaystyle A(t) = \begin{bmatrix} \mathrm{e}^{-t} & 0 \\ 0 & \mathrm{e}^t\end{bmatrix}\) に対して
- \(\displaystyle X(t) = \begin{bmatrix} \mathrm{e}^{-t} & 0 \\ 0 & 0\end{bmatrix}\) (\(t<0\)), \(\displaystyle X(t) = \begin{bmatrix} 0 & 0 \\ 0 & \mathrm{e}^{t} \end{bmatrix}\) (\(t>0\))
- \(\displaystyle Y(t) = \begin{bmatrix} \mathrm{e}^{-t} & 0 \\ 0 & 0\end{bmatrix}\) (\(t>t_0\))
\(t_0<0\) のときに \(Y(t_0)=X(t_0)\) として
近似問題を解いた解
このとき、\(t>0\) で \(X(t)\) と \(Y(t)\) の乖離は指数的に大きくなる
\(A(t)\) の特異値が \(t=0\) で交差するのが原因
微分方程式表現
(\(X(0) = U_0 S_0 V_0^\top\))
\(\dot{S} = U^\top \dot{A} V\)
\(\dot{U} = (I-UU^\top) \dot{A} V S^{-1}\)
\(\dot{V} = (I-VV^\top) \dot{A}^\top U S^{-\top}\)
\(S(0)=S_0\)
\(U(0) = U_0\)
\(V(0) = V_0\)
\(Y(t) = U(t) S(t) V(t)^\top\) は、近似問題の解を与える
- \(U(t)\) と \(V(t)\) は自動的に \(U(t)^\top U(t) = I\), \(V(t)^\top V(t) = I\)、
\(S(t)\) はランク \(k\) 行列となる - その帰結として、\(Y(t)=U(t)S(t)V(t)^\top\) もランク \(k\)
離散化の際の要点
(\(X(0) = U_0 S_0 V_0^\top\))
\(\dot{S} = U^\top \dot{A} V\)
\(\dot{U} = (I-UU^\top) \dot{A} V S^{-1}\)
\(\dot{V} = (I-VV^\top) \dot{A}^\top U S^{-\top}\)
\(S(0)=S_0\)
\(U(0) = U_0\)
\(V(0) = V_0\)
- \(U_n\) と \(V_n\) が \(U_n^\top U_n = I\), \(V_n^\top V_n = I\) をみたすように
離散化しなければならない - いろいろな方法が提案されている
最適化
最急降下法?
\(\bm{x}_{n+1} = \bm{x}_n - h_n \nabla f(\bm{x}_n)\)
最適化
数値解析
\(\displaystyle \min_{\bm{x}\in\mathbb{R}^d} f(\bm{x})\)
に対する最急降下法
\(\displaystyle \frac{\mathrm d}{\mathrm dt} \bm{x}(t) = - \nabla f(\bm{x}(t))\)
に対する陽的Euler法
\(h_n\) の決め方
目的
最適解の発見
関数値を基準に選ぶ
誤差を基準に選ぶ
厳密解フローの再現
連続最適化と微分方程式の数値解析
最適化問題
最適化問題
例:無制約最適化
\(\displaystyle \min_{\bm{x}\in\mathbb{R}^d} f(\bm{x})\)
最適化問題
微分方程式
例:勾配流
\(\dot{\bm{x}} = -\nabla f(\bm{x})\)
最適化問題
最適化手法
例:最急降下法
数値解法
例:陽的Euler法
\(\bm{x}_{n+1} = \bm{x}_n - h_n \nabla f(\bm{x}_n)\)
\(\bm{x}_{n+1} = \bm{x}_n - h_n \nabla f(\bm{x}_n)\)
他の例: Runge–Kutta法、線形多段解法
他の例: Nesterovの加速法、Newton法
最適解の探索
離散化
連 続 極 限
最適化に適した離散化手法?
適切なダイナミクス?
安定な陽解法の活用 1/5
目的関数 \(f\) についての仮定
- \(f\) が \(L\)-平滑 : 勾配 \(\nabla f\) が \(L\)-Lipschitz 連続
- \(\text{argmin}\ f \neq \emptyset\) : 最適解 \( \bm{x}^*\) が存在
- \(\mu\)-強凸 : \(\displaystyle f(\bm{x}) - \frac{\mu}{2}\|\bm{x}\|^2\) が凸関数
最急降下法の収束条件 (cf. Nesterov 2004)
\(h_n < 2/L\) のとき \( f(\bm{x}_n) \to f^*\)
安定な陽解法の活用 2/5
- 勾配流 \(\dot{\bm{x}} = -\nabla f(\bm{x})\) の線形化 : \(\dot{\bm{\delta}}=-\nabla^2 f(\bm{x})\bm{\delta}\)
- \(f\) が \(L\)-平滑な凸関数 \(\Rightarrow\) \(-\nabla^2 f(\bm{x})\) の固有値 \(\in [-L,2]\)

\(-2 < -Lh < 0\) ならば 陽的Euler法は安定
\(\Leftrightarrow 0<h<2/L\) : 最急降下法の収束条件と同じ!
安定性領域が実軸左方向に広がっている陽的RK法を使うと
より大きな刻み幅を使って安定に最適化問題を解けそう!
安定な陽解法の活用 3/5

(引用:Hairer, Wanner, Solving Ordinary Differential Equations II)
Text
こういう点は避けたい

左端 \(\approx 2s^2\)
安定な陽解法の活用 4/5
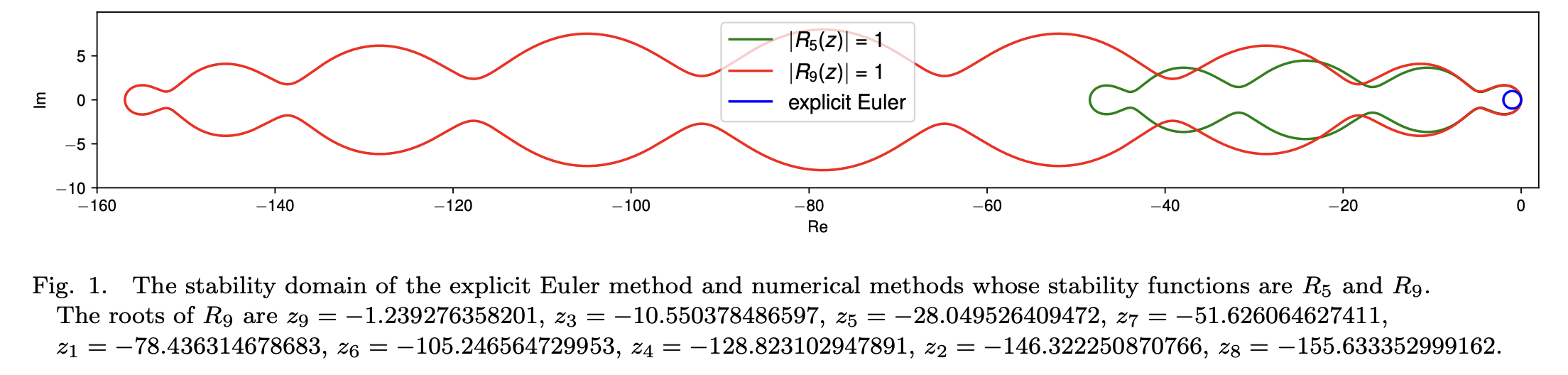
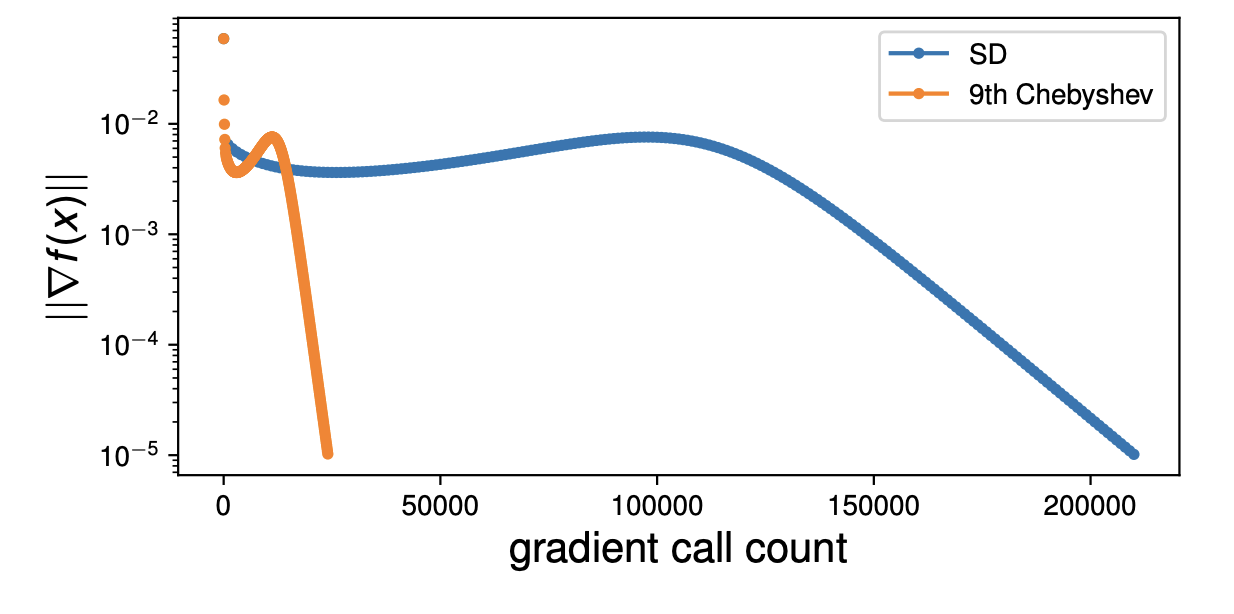
安定な陽解法の活用 5/5

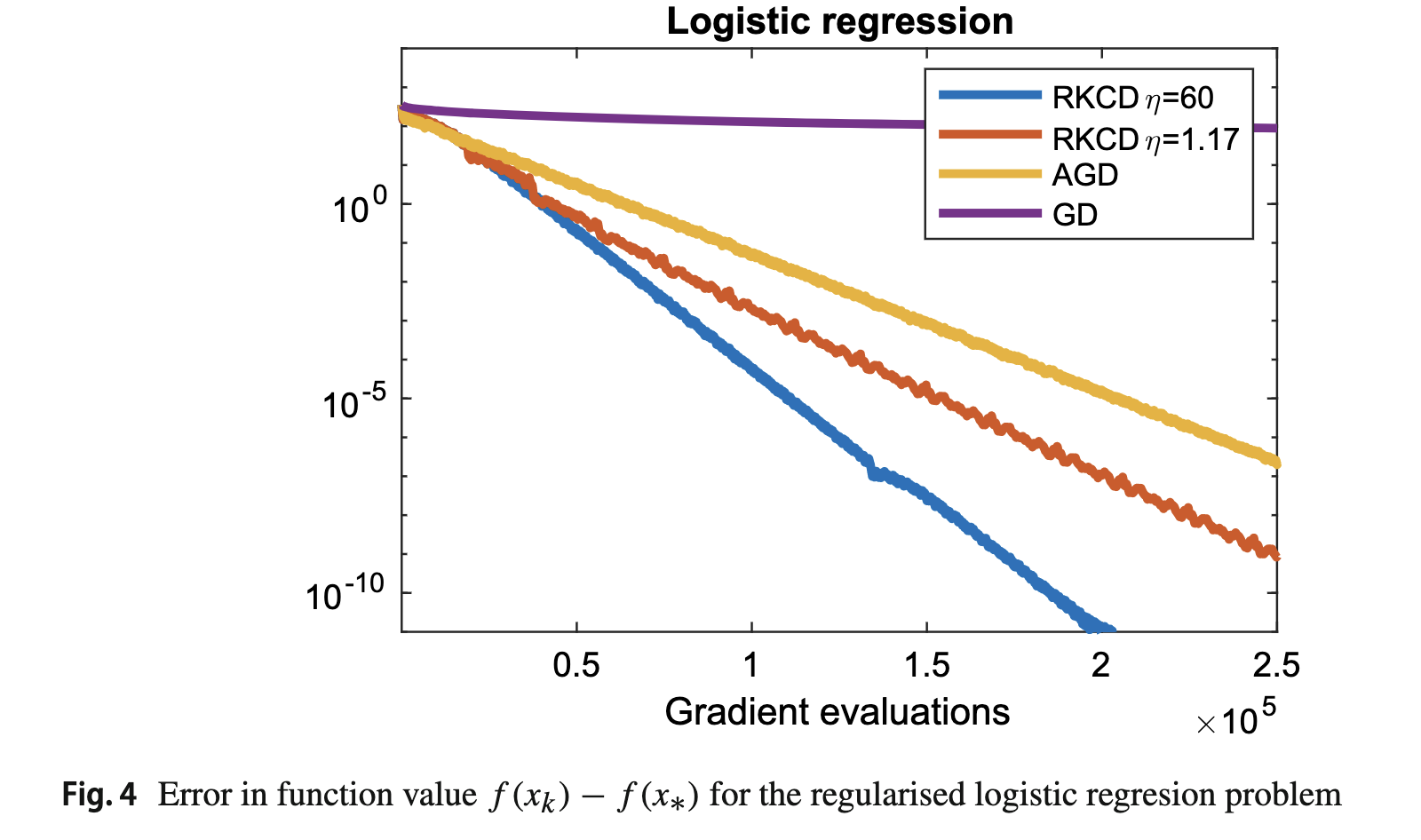
離散勾配法の活用 1/4
ところで、刻み幅の制約を受けない陽的な解法は作れないだろうか?
A. 可能!
観察:勾配系 \(\dot{\bm{x}} = -\nabla f(\bm{x})\) に対して \(f(\bm{x}(t))\) は単調減少
\( \displaystyle \frac{\mathrm d}{\mathrm dt} f(\bm{x}) = \nabla f(\bm{x}) ^\top \dot{\bm{x}} = - \| \nabla f(\bm{x})\|^2 \leq 0\)
方程式の代入 (自明)
連鎖律 (本質)
離散勾配法の活用 2/4
連鎖律 \( \displaystyle \frac{\mathrm d}{\mathrm dt} f(\bm{x}) = \nabla f(\bm{x}) ^\top \dot{\bm{x}}\) を模倣して
- \( \displaystyle f(\bm{y})-f(\bm{x}) = \nabla_\text{d} f(\bm{x},\bm{y}) ^\top ( \bm{y} - \bm{x})\)
- \( \nabla_\text{d}f(\bm{x},\bm{x}) = \nabla f(\bm{x})\)
を満たす離散量 \( \nabla_\text{d} f(\bm{x},\bm{y})\) を用いて
勾配流 \(\dot{\bm{x}} = -\nabla f(\bm{x})\) を
\(\displaystyle \frac{\bm{x}_{n+1}-\bm{x}_n}{h} = -\nabla_\text{d} f(\bm{x}_n,\bm{x}_{n+1})\)
と離散化すると
\(\displaystyle f(\bm{x}_{n+1})-f(\bm{x}_n)=\big(\nabla_\text{d} f(\bm{x}_n,\bm{x}_{n+1})\big)^\top (\bm{x}_{n+1}-\bm{x}_n) = -h \| \nabla_\text{d}\bm{f}\|^2 \leq 0\)
\(0<h\) でありさえすれば、\(f\) は単調減少

離散勾配法
離散勾配法の活用 3/4
- 一般に離散勾配は無数に存在する
ほとんどの場合、陰解法になる

脱線??
SOR法 (Successive Over-Relaxation法、逐次加速緩和法)
- 連立一次方程式 \( A \bm{x} = \bm{b}, \ \ A \in \mathbb{R}^{m\times m}, \ \bm{b} \in \mathbb{R}^m\) に対する代表的な定常反復法
- \(\bm{x}^{(n+1)} \mapsto \bm{x}^{(n)}\) の定義:
\(\displaystyle \bm{x}_i^{(m+1)}=(1-\omega)\bm{x}_i^{(n)} + \omega \frac{1}{a_{ii}} \big( b_i - \sum_{j=1}^{i-1}a_{ij}\bm{x}_j^{(k+1)} - \sum_{j=i}^{m}a_{ij}\bm{x}_j^{(k)} \big),\) \(i=1,\dots,m\)
- \(\omega=1\) のとき、Gauss–Seidel法; \(\omega\):緩和パラメータ
- \(A\) が正定値対称行列のとき、
SOR法が任意の初期ベクトル \(\bm{x}^{(0)}\) に対して収束 \(\Leftrightarrow\) \(\omega\in (0,2)\)
離散勾配法の活用 4/4
- \(\dot{\bm{x}} = - D^{-1} \nabla f(\bm{x}) (= -D^{-1} (A\bm{x}-\bm{b}) ) \)
を Itoh–Abeの離散勾配 を用いて離散化すると
\(A\) が正定値対称ならば、\(0<h_n\) でありさえすれば収束する - \(\displaystyle h=\frac{2\omega}{2-\omega}\) と変換すれば、SOR法と一致!

SOR法の連続極限
画像処理
(ちょっとだけ)
画像処理に微分方程式?
- ODE Net を使うと自然に微分方程式が登場
- 離散勾配法を用いるなど、微分方程式を介して
最適化アルゴリズムを導出
- 画像処理の過程そのものを微分方程式でモデル化
例 : Inpainting (画像修復)
最後に...重要そうな文献をいくつか
常微分方程式の数値解析の基礎
和書で、入門書よりは深く、
一方で専門的過ぎない
定番の教科書:1990年代半ばくらいまでの研究内容が
網羅的に整理されている
常微分方程式の数値解析の基礎
(第3版は) より最先端の内容も含んでいる
PDEも扱っている
構造保存数値解法
対象はHamilton系が中心
(やや古く、対象が限定的)
数学的にはHLWほど高度ではない
定番中の定番
数学的難易度はやや高め
一番新しい
対象はやや限定的だが読みやすい
まとめ
- 微分方程式を扱う際は、ほとんどの場合、離散化が必須
数値解析のいろいろな手法が (数値解析で忘れられているような手法も) 役立つ!

数値解析学者として嬉しい!
- これまでの数値解析学の知見では不十分なことも多い
(例)
近年、「低精度演算」の需要が大きかったりする
新しい数値解析学的研究テーマ

数値解析学者として嬉しい!

阪大での講義資料










