Safety and Efficiency in Autonomous Vehicles through Planning with Uncertainty

Zachary Sunberg

May 25, 2018

image/svg+xml

Introduction

UAV Collision Avoidance

Lane Changing with Internal States

Solving Continuous POMDPs

POMDPs.jl

Controlling an Autonomous Vehicle is inherently a multi-objective problem

EFFICIENCY

SAFETY

Minimize resource use

(especially time)

Minimize the risk of harm to oneself and others

Increasing safety can only decrease efficiency

Two extremes:

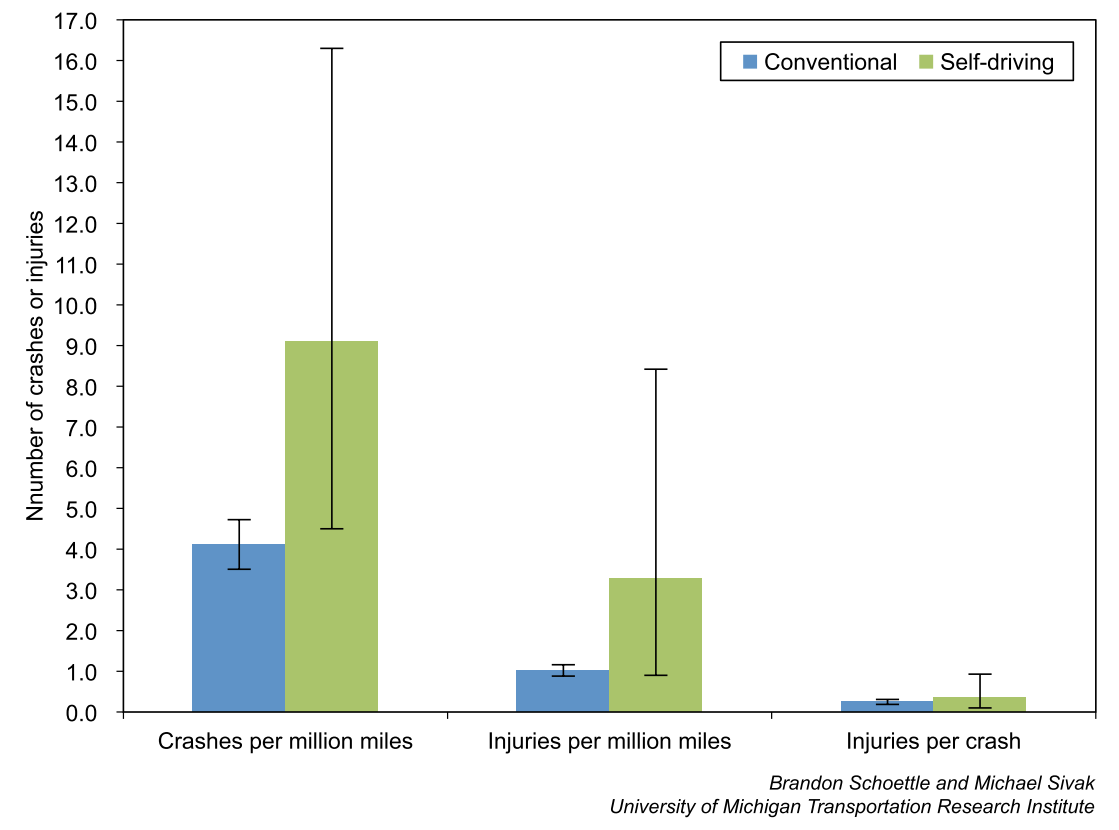
XXX Credit

“self-driving vehicles were not at fault in any crashes they were involved in.”

XXX Credit

PLANNING UNDER UNCERTAINTY

HARD SAFETY CONSTRAINTS

  1. Objective
  2. Dynamic Model
  3. Optimization Algorithm

A systematic approach:

Objective: maximize future reward

$$\mathop{\text{maximize}} E\left[\sum_{t=0}^{\infty} \gamma^t r_t\right]$$

$$r_t = R(s_t, a_t, s_{t+1})$$

How do we optimize both safety and efficiency?

Objective Function

$$R(s_t, a_t, s_{t+1}) = R_\text{E}(s_t, a_t, s_{t+1}) + \lambda R_\text{S}(s_t, a_t, s_{t+1})$$

Safety

Weight

Efficiency

Safety

Better Performance

Model \(M_2\), Algorithm \(A_2\)

Model \(M_1\), Algorithm \(A_1\)

Efficiency

Dynamic Model: Types of Uncertainty

Outcome

Model

State

State Transitions

Observations

State Transition Distribution

Observation Distribution

Reward

Markov Model

  • \(\mathcal{S}\) - State space
  • \(T:\mathcal{S}\times\mathcal{S} \to \mathbb{R}\) - Transition probability distributions

Markov Decision Process (MDP)

  • \(\mathcal{S}\) - State space
  • \(T:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Transition probability distribution
  • \(\mathcal{A}\) - Action space
  • \(R:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Reward Function

Partially Observable Markov Decision Process (POMDP)

  • \(\mathcal{S}\) - State space
  • \(T:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Transition probability distribution
  • \(\mathcal{A}\) - Action space
  • \(R:\mathcal{S}\times \mathcal{A} \times\mathcal{S} \to \mathbb{R}\) - Reward Function
  • \(\mathcal{O}\) - Observation space
  • \(Z:\mathcal{S} \times \mathcal{A}\times \mathcal{S} \times \mathcal{O} \to \mathbb{R}\) - Observation probability distribution

Belief

\[b'(s') = \frac{\int_{s\in\mathcal{S}} Z(o \mid s, a, s') T(s' \mid s, a) b(s) ds}{\int_{s'\in\mathcal{S}} \int_{s\in\mathcal{S}} Z(o \mid s, a, s') T(s' \mid s, a) b(s) ds ds'}\]

History: all previous actions and observations

\[h_t = (b_0, a_0, o_1, a_1, o_2, ..., a_{t-1}, o_t)\]

Belief: probability distribution over \(\mathcal{S}\) encoding everything learned about the state from the history

\[b_t(s) = P(s_t=s \mid h_t)\]

A POMDP is an MDP on the belief space.

Solving MDPs and POMDPs - The Value Function

$$\mathop{\text{maximize}} V_\pi(s) = E\left[\sum_{t=0}^{\infty} \gamma^t r_t \bigm| s_0 = s, a_t = \pi(s_t) \right]$$

$$V^*(s) = \max \left\{R(s, \pi(s)) + \gamma E\Big[V^*\left(s_{t+1}\right) \mid s_t=s, a_t=\pi(s)\Big]\right\}$$

\pi: \mathcal{S} \to \mathcal{A}
π:S→A\pi: \mathcal{S} \to \mathcal{A}

Involves all future time

Involves only \(t\) and \(t+1\)

$$Q_\pi(s, a) = E\left[\sum_{t=0}^{\infty} \gamma^t r_t \bigm| s_0 = s, a_0 = a, a_t = \pi(s_t)\right]$$

$$V^*(s) = \max_{a \in \mathcal{A}} Q^*(s,a)$$

Solving MDPs and POMDPs - Offline vs Online

Offline

(Value Iteration)

Online

(Sequential Decision Tree)

QMDP

\[Q_{MDP}(b, a) = \sum_{s \in \mathcal{S}} Q_{MDP}(s,a) b(s) \geq Q^*(b,a)\]

Equivalent to assuming full observability on the next step.

Will not take costly exploratory actions.

image/svg+xml

Introduction

UAV Collision Avoidance

Lane Changing with Internal States

Solving Continuous POMDPs

POMDPs.jl

Trusted and Optimized UAV Collision Avoidance

Challenge 1: Horizontal maneuvers

Traditional Solution: Altitude Separation

UAVs Require Horizontal Maneuvers

Challenge 2: Certification

  • Government agencies and vehicle operators often seek certification that a control system will never command a dangerous action.
  • Simple, deterministic algorithms are much easier to certify.

Bach, R., Farrell, C., & Erzberger, H. (2009). An Algorithm for Level-Aircraft Conflict Resolution.

Additional buffer compensates for uncertainty

1.0

1.5

2.0

3.0

4.0

MDP Formulation

\(s=\left(x^{(o)}, y^{(o)}, \psi^{(o)}, x^{(i)}, y^{(i)}, \psi^{(i)}, \text{dev}\right)\)

\(a = \phi^{(o)}\), \(\mathcal{A} = \{-45^\circ, -22.5^\circ, 0^\circ, 22.5^\circ, 45^\circ\}\)

\(R(s, a) = -c_\text{step} + r_\text{goal} \, \text{in\_goal}(s) - c_\text{dev} \, \text{dev}(s,a) - \lambda \,\text{nmac}(s) \)

Transition: \(\quad \dot{\psi}^{(o)}_t = \frac{g \, \tan \phi^{(o)}_t}{v^{(o)}}\), \(\quad \dot{\psi}^{(i)}_t \sim \mathcal{N}(0, 10^\circ/s)\)

Ownship State

Intruder State

Bank Angle

Approximate Value Iteration

\[\tilde{V}(s) = \beta(s)^\top \theta\]

 

\[\tilde{V}_{k+1}(s) = \Pi \mathcal{B}[\tilde{V}_k](s)\]

 

At each iteration, sample \(N_\text{state}\) states and estimate the value with

\[v_{k+1}[n] \gets \max_{a \in \mathcal{A}} \left\{R(s^{[n]},a) + \frac{1}{N_{\text{EV}}}\sum_{m=1}^{N_{\text{EV}}} \beta(F(s^{[n]}, a, w_m))^\top \theta_k \right\} \text{,}\]

then, project onto the linear subspace with

\[\theta_{k+1} = \text{argmin} \sum_{n=1}^{N_\text{state}} \left( \beta\left(s^{[n]}\right)^\top \theta - v_{k+1}[n] \right) ^2 \text{.}\]

Features

Value Function and Policy

\(45^\circ\)

\(-45^\circ\)

\(\phi=0^\circ\)

Price of certifiability

Trusted Resolution Logic

Directly Optimized Turn Rate

Maintaining certifiability

\[\tilde{\mathcal{A}}(s) = \left\{a \in \mathcal{A} \mid \text{mindist}(s, a) \geq D_\text{NMAC} \right\}\]

Price of certifiability

Trusted Resolution Logic

Directly Optimized Turn Rate

Trusted Optimized Turn Rate

image/svg+xml

Introduction

UAV Collision Avoidance

Lane Changing with Internal States

Solving Continuous POMDPs

POMDPs.jl

Tweet by Nitin Gupta

29 April 2018

https://twitter.com/nitguptaa/status/990683818825736192

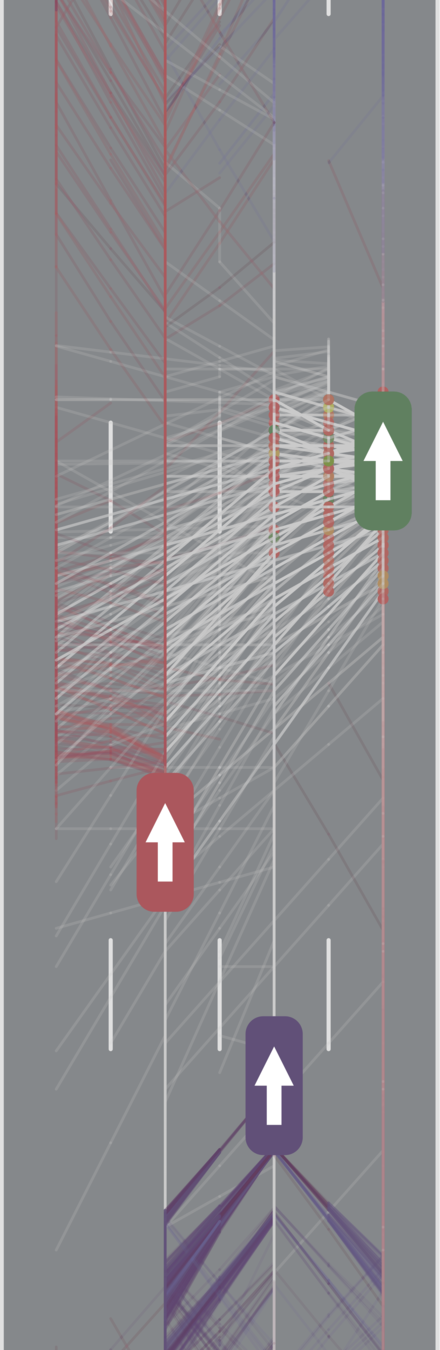
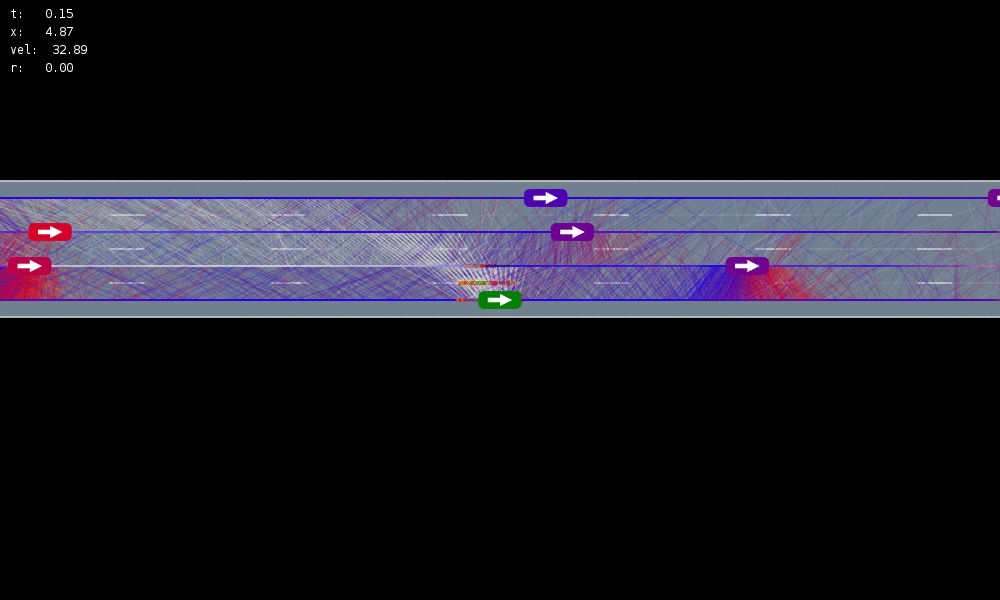
Human Behavior Model: IDM and MOBIL

\ddot{x}_\text{IDM} = a \left[ 1 - \left( \frac{\dot{x}}{\dot{x}_0} \right)^{\delta} - \left(\frac{g^*(\dot{x}, \Delta \dot{x})}{g}\right)^2 \right]
x¨IDM=a[1−(x˙x˙0)δ−(g∗(x˙,Δx˙)g)2] \ddot{x}_\text{IDM} = a \left[ 1 - \left( \frac{\dot{x}}{\dot{x}_0} \right)^{\delta} - \left(\frac{g^*(\dot{x}, \Delta \dot{x})}{g}\right)^2 \right]
g^*(\dot{x}, \Delta \dot{x}) = g_0 + T \dot{x} + \frac{\dot{x}\Delta \dot{x}}{2 \sqrt{a b}}
g∗(x˙,Δx˙)=g0+Tx˙+x˙Δx˙2abg^*(\dot{x}, \Delta \dot{x}) = g_0 + T \dot{x} + \frac{\dot{x}\Delta \dot{x}}{2 \sqrt{a b}}

POMDP Formulation

\(s=\left(x, y, \dot{x}, \left\{(x_c,y_c,\dot{x}_c,l_c,\theta_c)\right\}_{c=1}^{n}\right)\)

\(o=\left\{(x_c,y_c,\dot{x}_c,l_c)\right\}_{c=1}^{n}\)

\(a = (\ddot{x}, \dot{y})\), \(\ddot{x} \in \{0, \pm 1m/s^2\}, \dot{y} \in \{0, \pm 0.67 m/s^2\}\)

R(s, a, s') = \text{in\_goal}(s') - \lambda \, \text{any\_hard\_brakes}(s, s') - \lambda \, \text{any\_too\_slow}(s')
R(s,a,s′)=in_goal(s′)−λany_hard_brakes(s,s′)−λany_too_slow(s′)R(s, a, s') = \text{in\_goal}(s') - \lambda \, \text{any\_hard\_brakes}(s, s') - \lambda \, \text{any\_too\_slow}(s')

Ego physical state

Physical states of other cars

Internal states of other cars

Physical states of other cars

  • Actions filtered so they can never cause crashes
  • Braking action always available

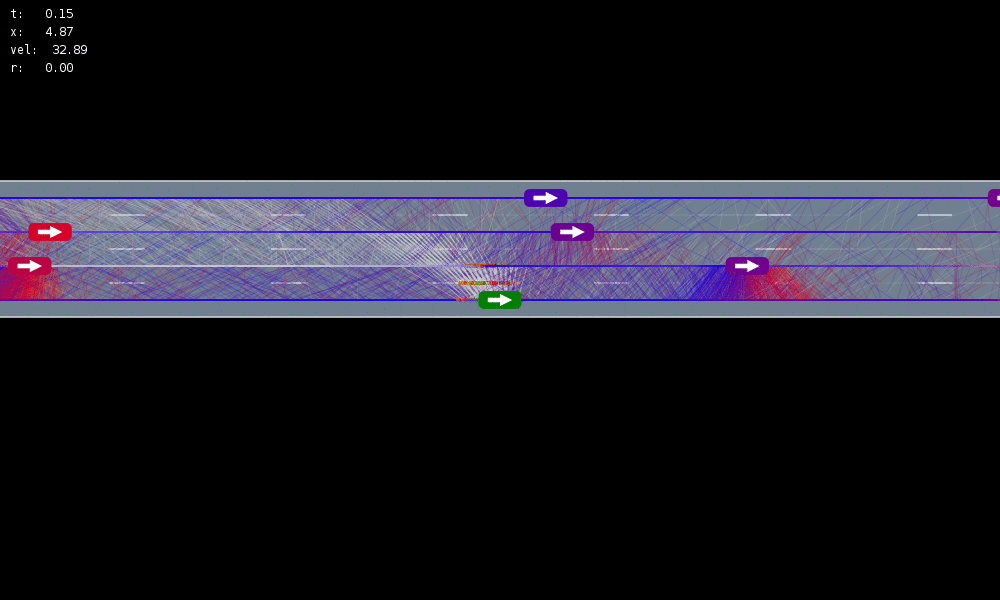
Assume normal

Outcome only

Omniscient

Mean MPC

QMDP

POMCPOW

Simulation results

Assume normal

Outcome only

Omniscient

Mean MPC

QMDP

POMCPOW

Assume normal

Omniscient

Mean MPC

QMDP

POMCPOW

image/svg+xml

Introduction

UAV Collision Avoidance

Lane Changing with Internal States

Solving Continuous POMDPs

POMDPs.jl

Monte Carlo Tree Search

POMCP

  • Uses simulations of histories instead of full belief updates

 

  • Each belief is implicitly represented by a collection of unweighted particles

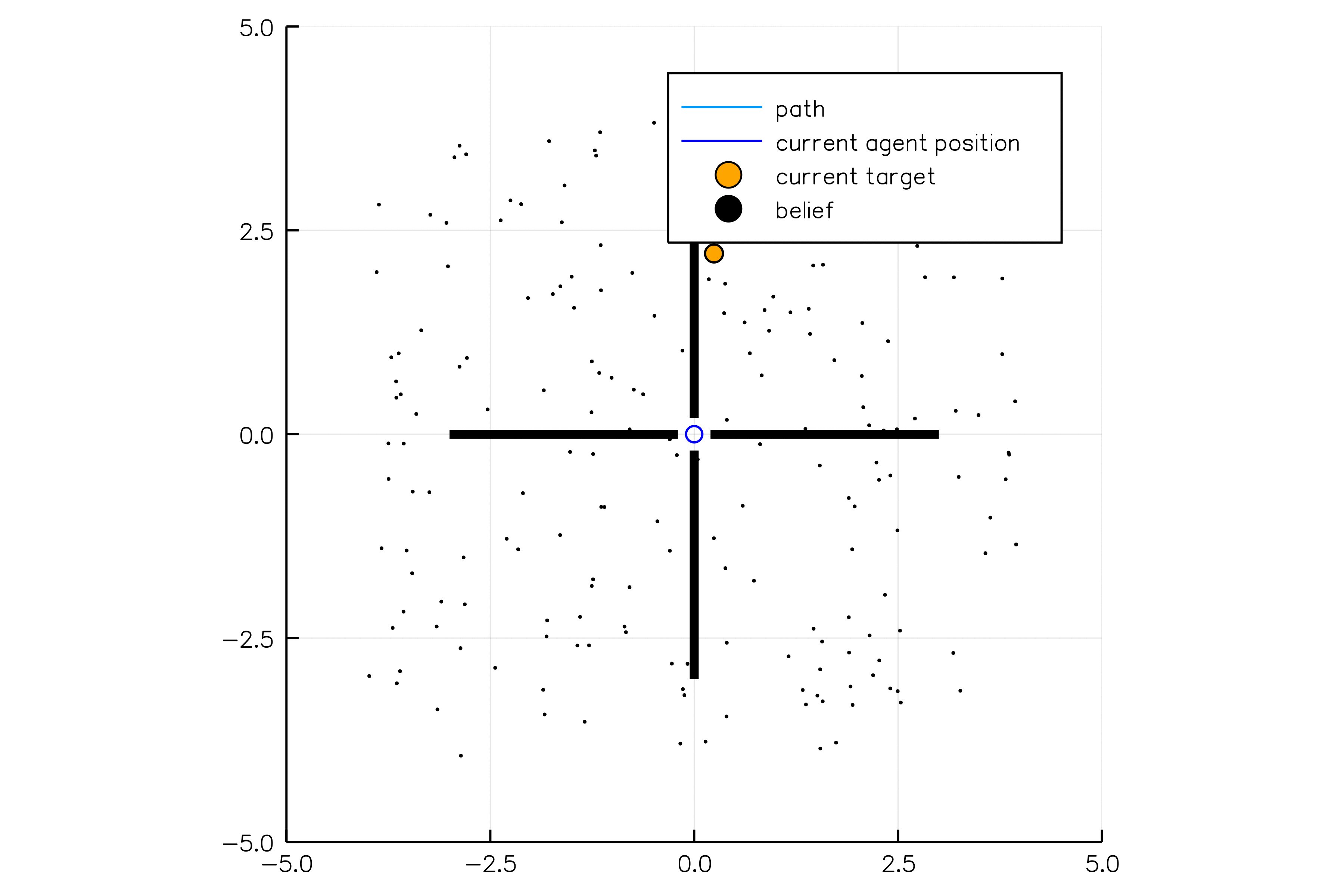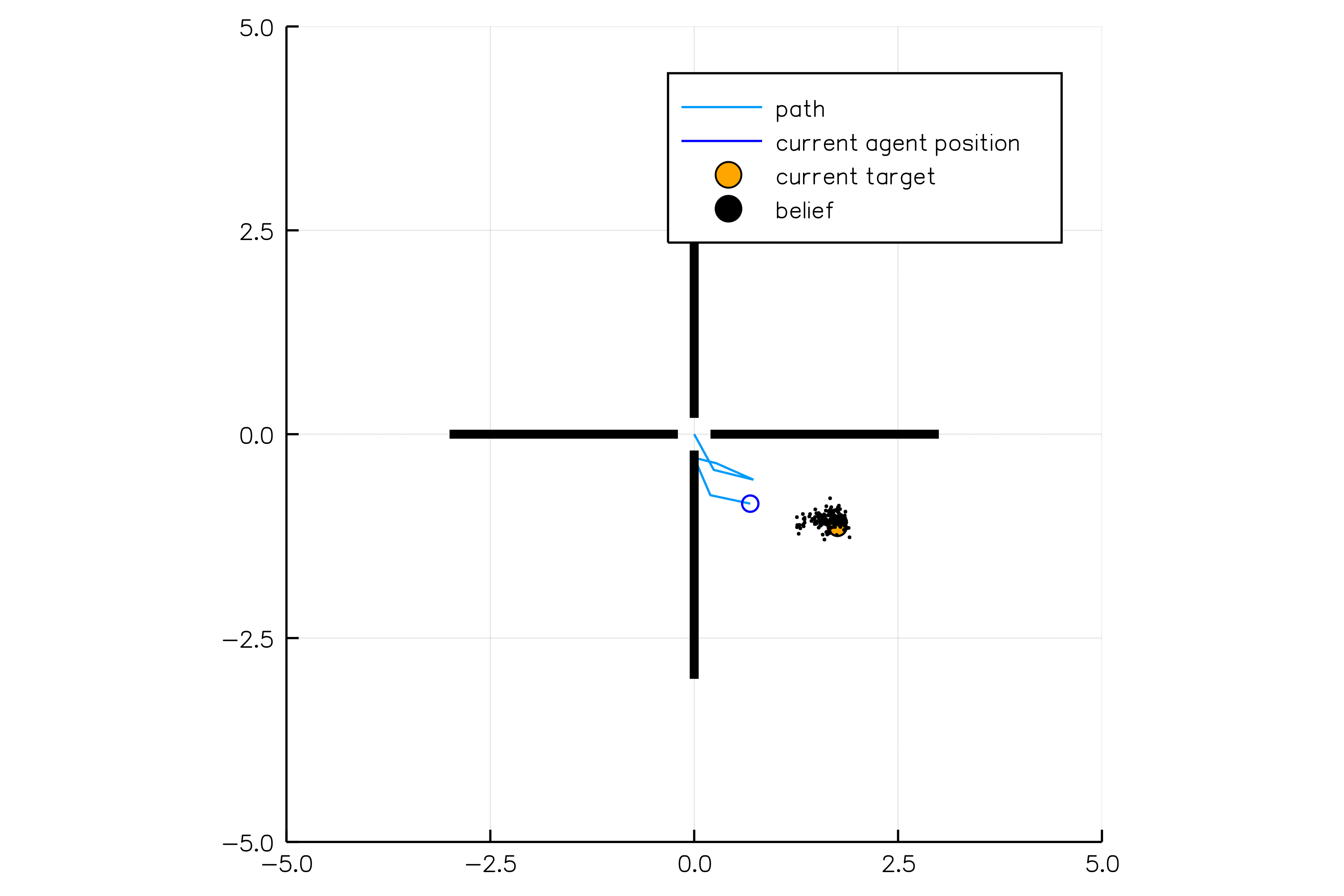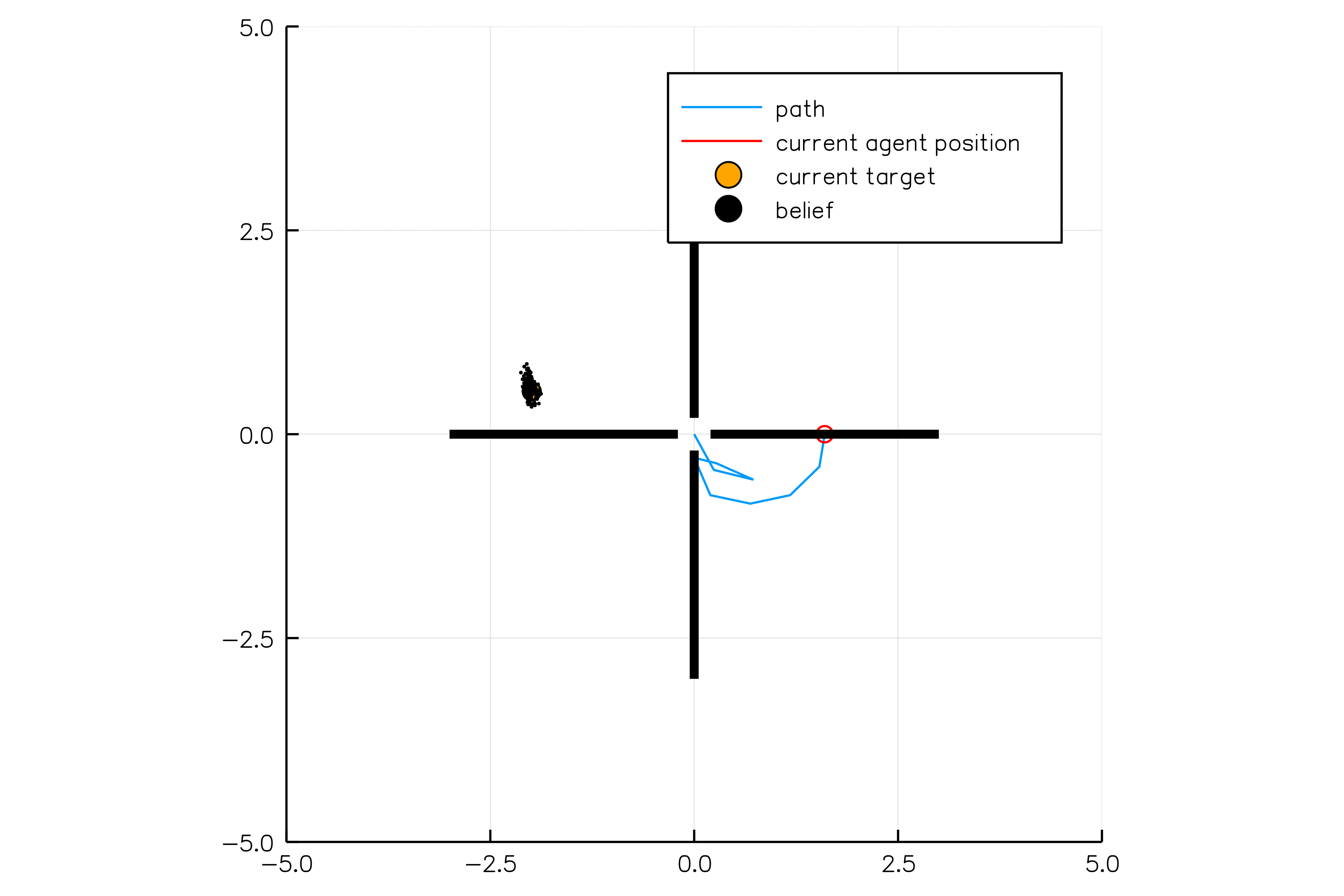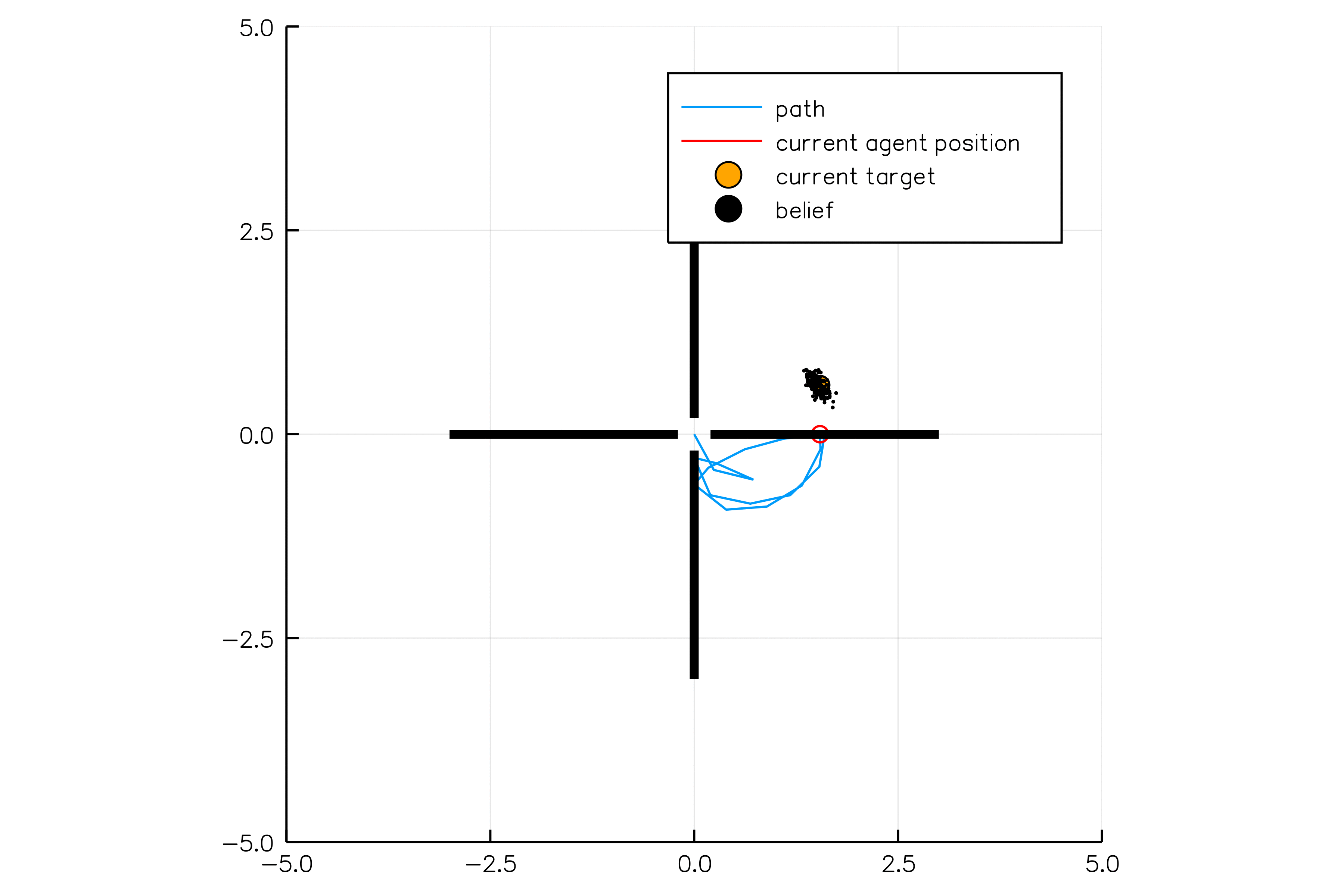
Light-Dark Problem

\begin{aligned} & \mathcal{S} = \mathbb{Z} \quad \quad \quad ~~ \mathcal{O} = \mathbb{R} \\ & s' = s+a \quad \quad o \sim \mathcal{N}(s, s-10) \\ & \mathcal{A} = \{-10, -1, 0, 1, 10\} \\ & R(s, a) = \begin{cases} 100 & \text{ if } a = 0, s = 0 \\ -100 & \text{ if } a = 0, s \neq 0 \\ -1 & \text{ otherwise} \end{cases} & \\ \end{aligned}
S=Z  O=Rs′=s+ao∼N(s,s−10)A={−10,−1,0,1,10}R(s,a)={100 if a=0,s=0−100 if a=0,s≠0−1 otherwise\begin{aligned} & \mathcal{S} = \mathbb{Z} \quad \quad \quad ~~ \mathcal{O} = \mathbb{R} \\ & s' = s+a \quad \quad o \sim \mathcal{N}(s, s-10) \\ & \mathcal{A} = \{-10, -1, 0, 1, 10\} \\ & R(s, a) = \begin{cases} 100 & \text{ if } a = 0, s = 0 \\ -100 & \text{ if } a = 0, s \neq 0 \\ -1 & \text{ otherwise} \end{cases} & \\ \end{aligned}

State

Timestep

Accurate Observations

Goal: \(a=0\) at \(s=0\)

Optimal Policy

Localize

\(a=0\)

Necessary Conditions for Consistency [1]

 

[  ] An infinite number of child nodes must be visited

[  ] Each node must be visited an infinite number of times

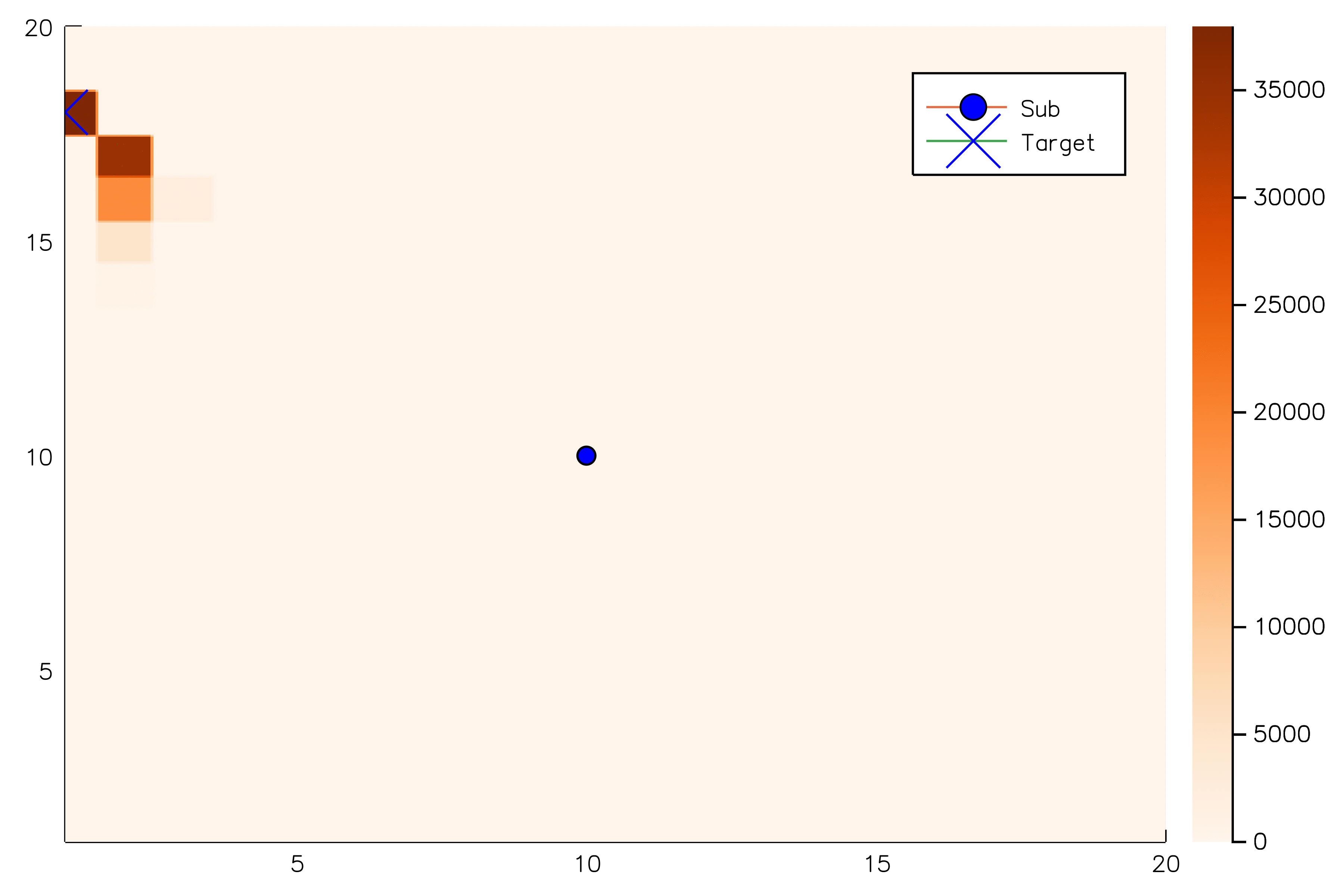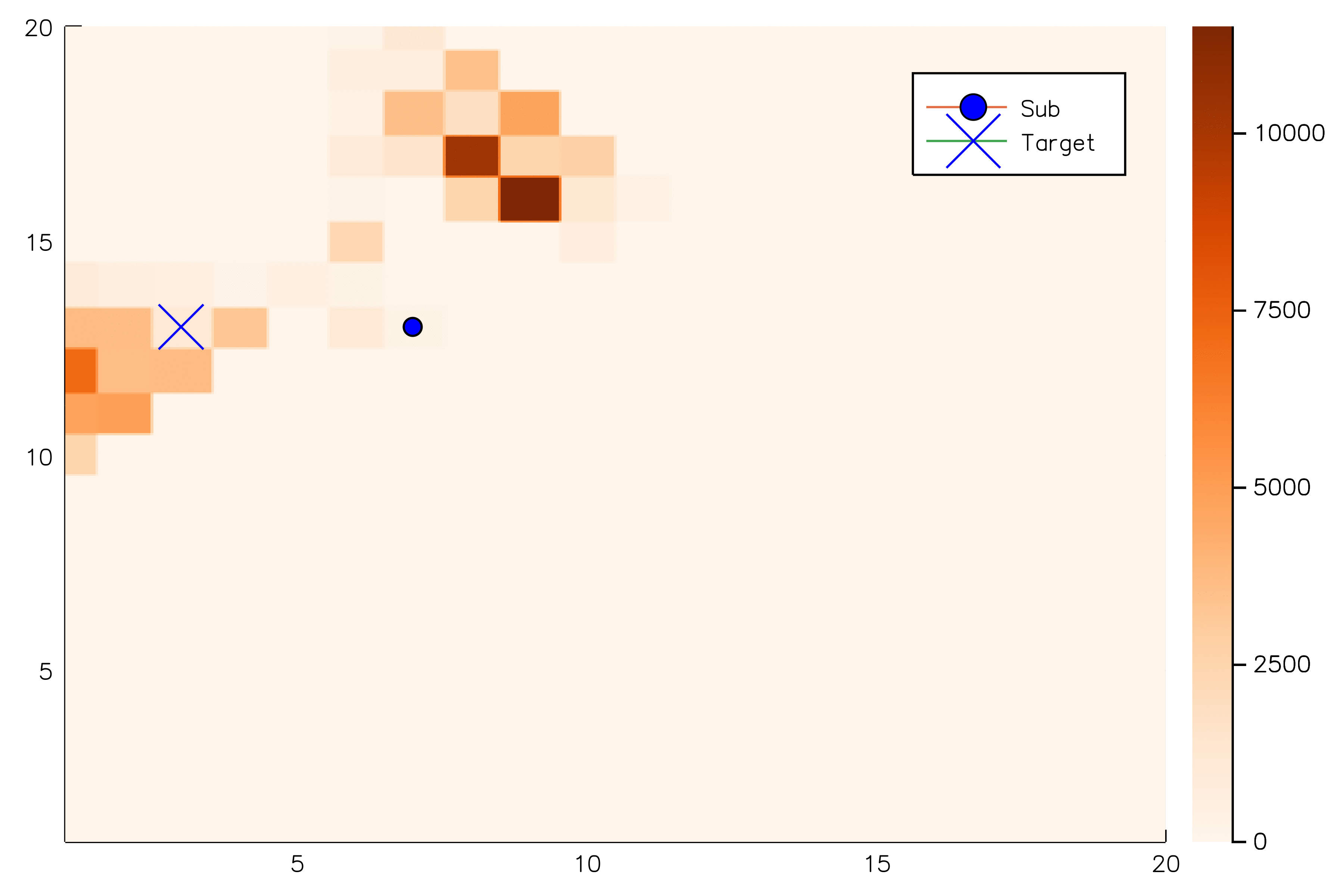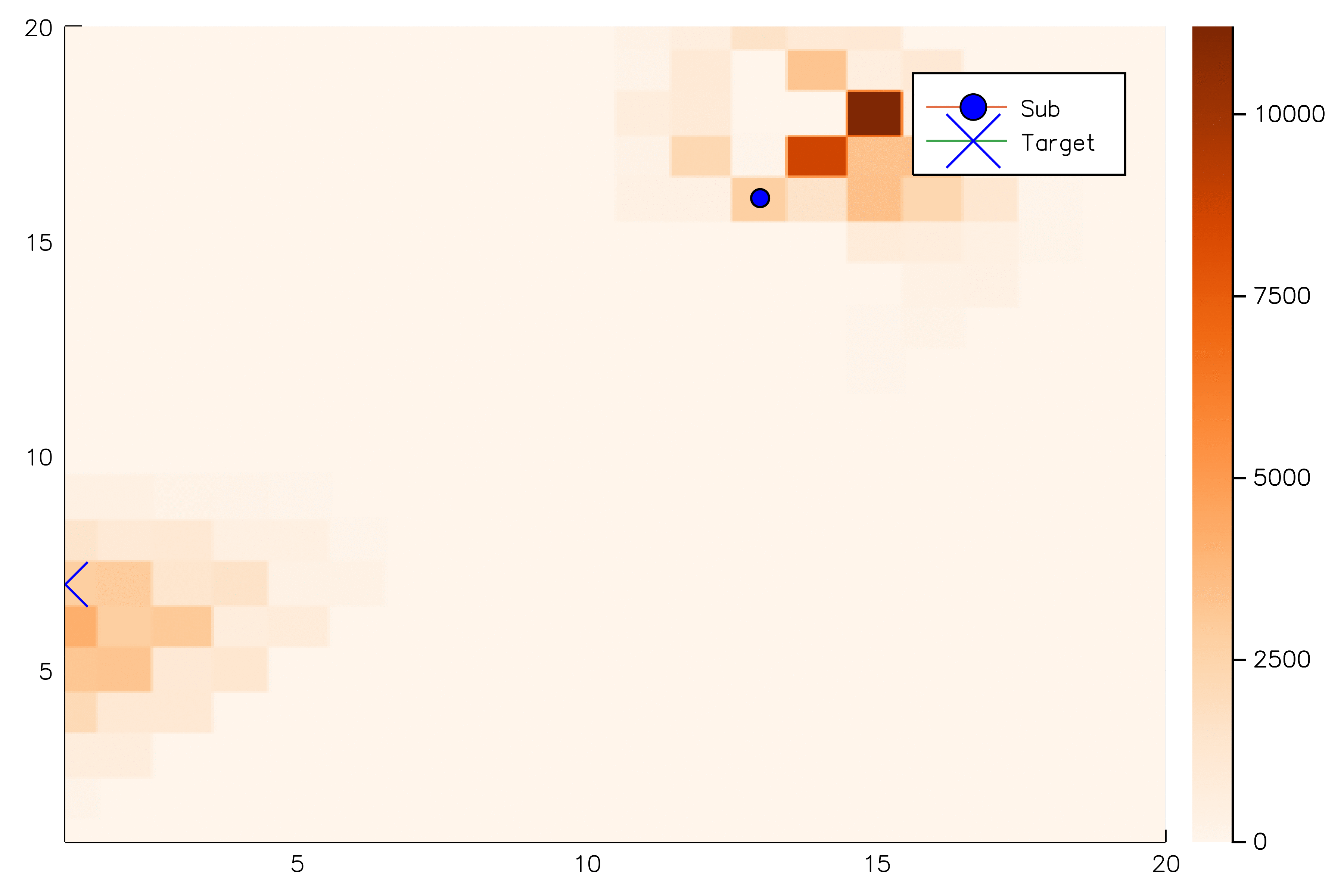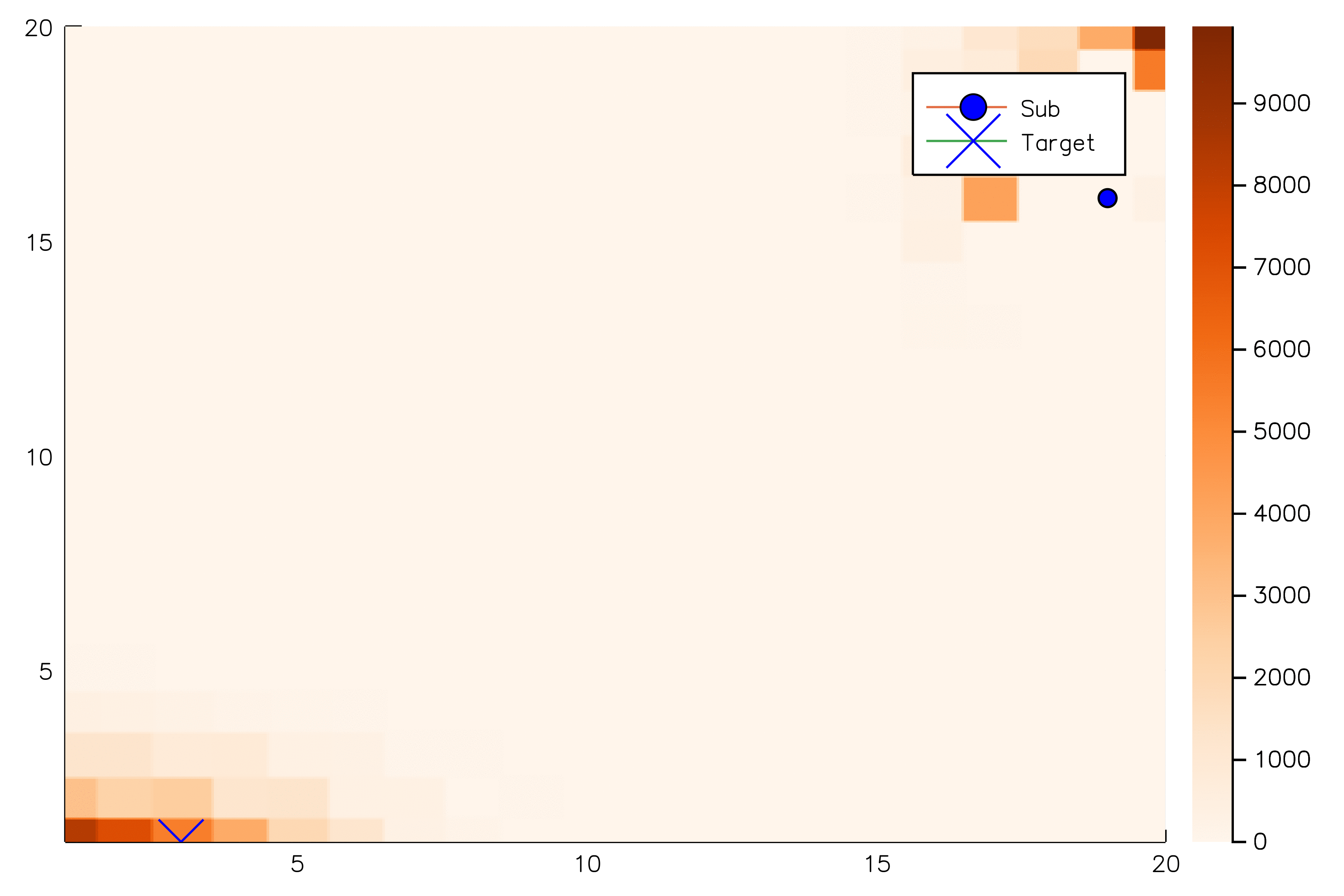
Solving continuous POMDPs - POMCP fails

[1] Adrien Coutoux, Jean-Baptiste Hoock, Nataliya Sokolovska, Olivier Teytaud, Nicolas Bonnard. Continuous Upper Confidence Trees. LION’11: Proceedings of the 5th International Conference on Learning and Intelligent OptimizatioN, Jan 2011, Italy. pp.TBA. <hal-00542673v2>

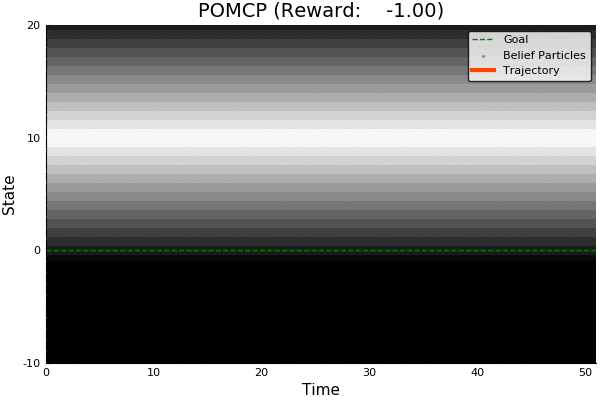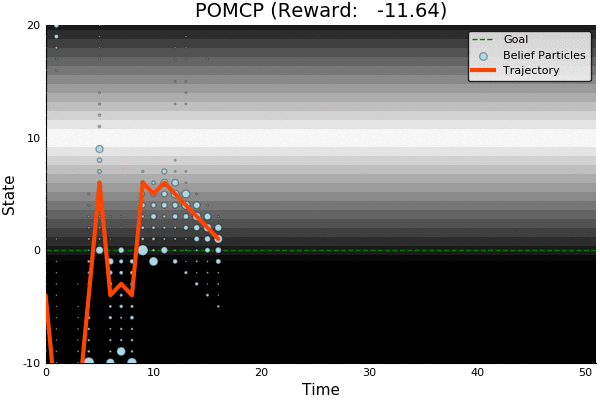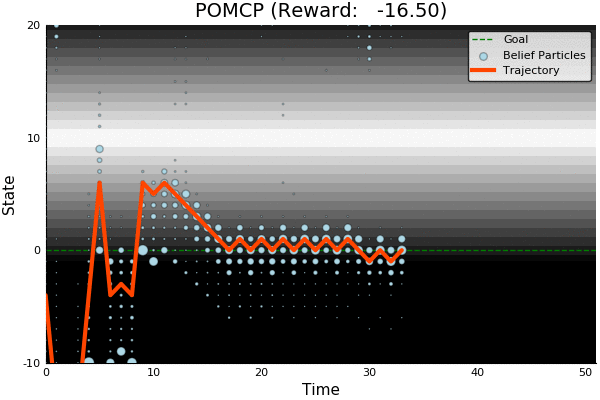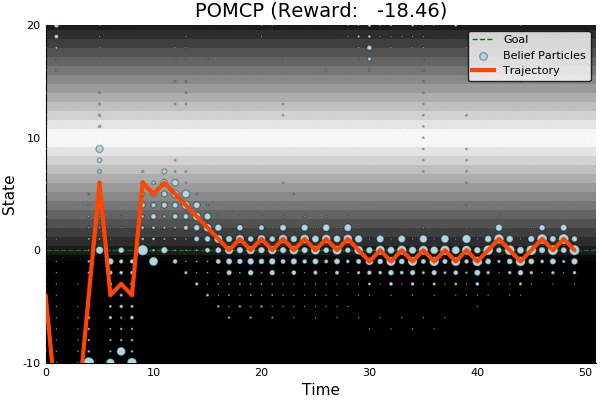
POMCP

✔

✔

Limit number of children to

\[k N^\alpha\]

POMCP

POMCP-DPW

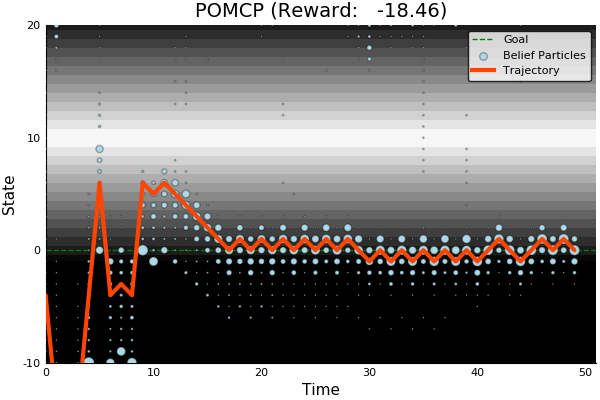
POMCP-DPW converges to QMDP

Proof Outline:

  1. Observation space is continuous → observations unique w.p. 1.

  2. (1) → One state particle in each belief, so each belief is merely an alias for a that state

  3. (2) → POMCP-DPW = MCTS-DPW applied to fully observable MDP + root belief state

  4. Solving this MDP is equivalent to finding the QMDP solution → POMCP-DPW converges to QMDP

POMCP-DPW

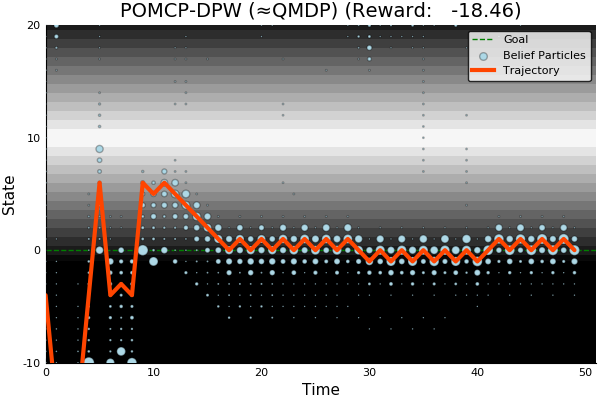
Necessary Conditions for Consistency

 

[  ] An infinite number of child nodes must be visited

[  ] Each node must be visited an infinite number of times

[  ] An infinite number of particles must be added to each belief node

✔

✔

✔

Use \(Z\) to insert weighted particles

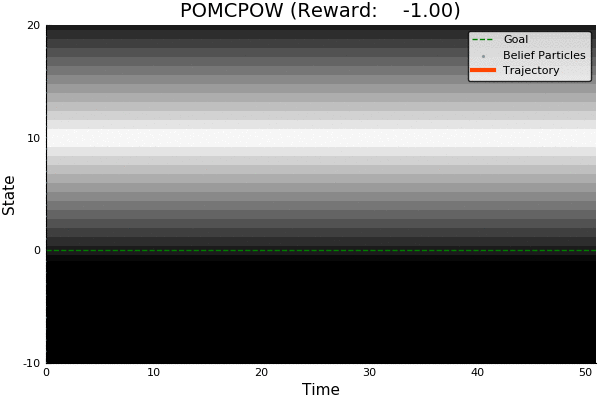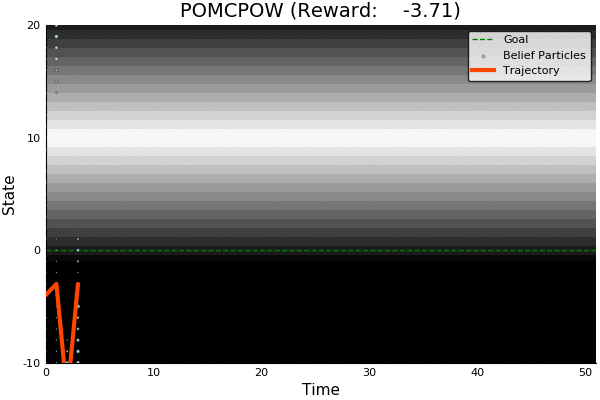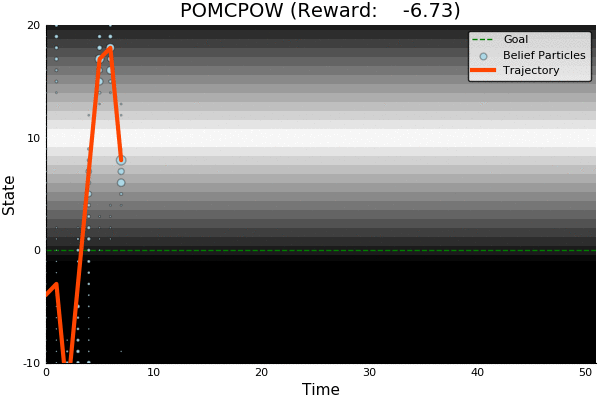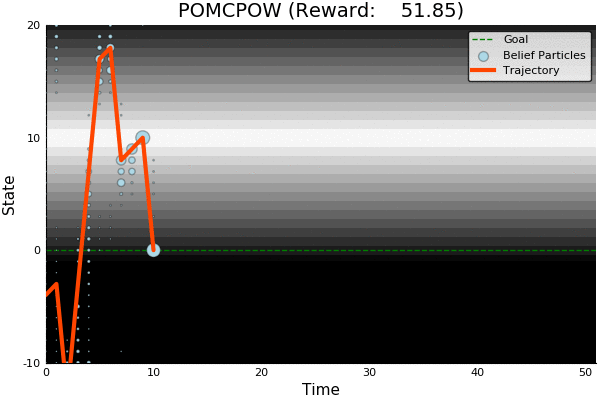
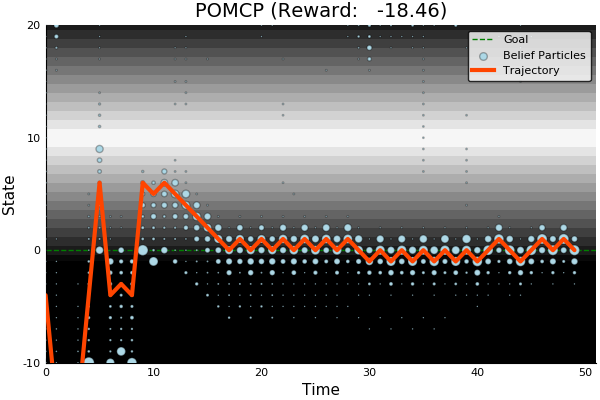
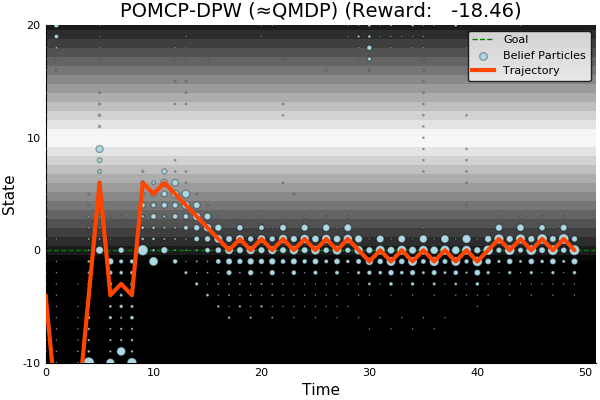
POMCP

POMCP-DPW

POMCPOW

image/svg+xml

Introduction

UAV Collision Avoidance

Lane Changing with Internal States

Solving Continuous POMDPs

POMDPs.jl

Previous C++ framework: APPL

"At the moment, the three packages are independent. Maybe one day they will be merged in a single coherent framework."

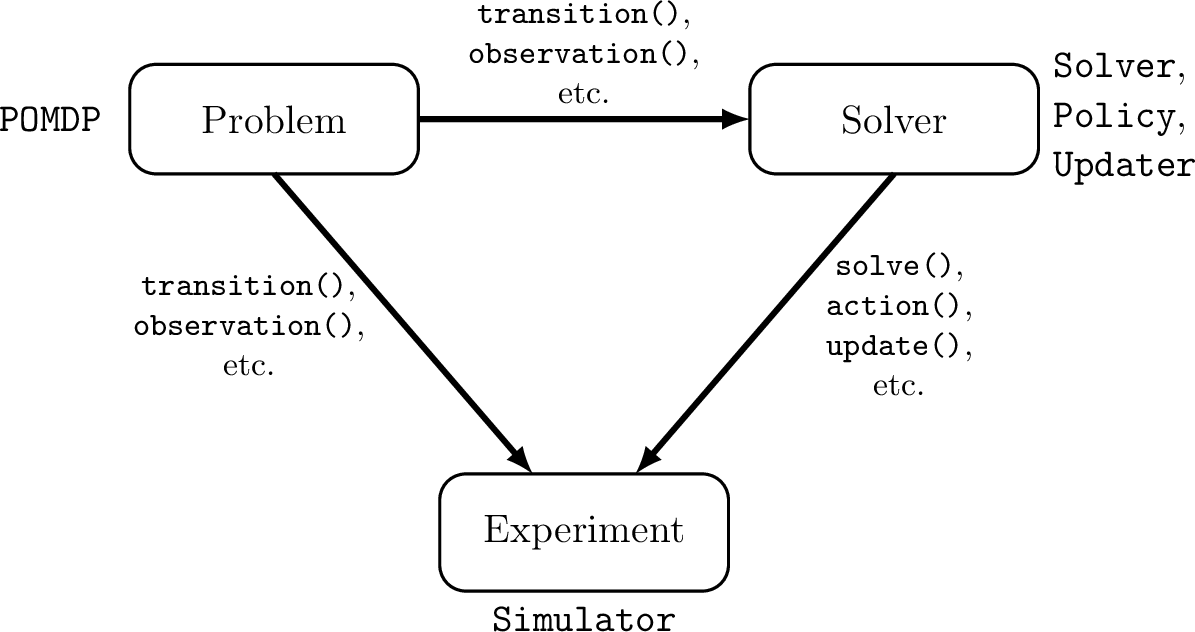
POMDPs.jl - An interface for defining and solving MDPs and POMDPs in Julia

Contributions

  1. Quantified the price of certifiability for a UAV collision avoidance system and showed how to reduce it.
  2. Quantified the safety and efficiency advantage of planning with internal states.
  3. Developed online algorithms for continuous POMDPs.
    1. Showed that current solvers and naive double progressive widening are suboptimal.
    2. Used weighted particle filtering to achieve first performance better than QMDP.
  4. Led development of POMDPs.jl
image/svg+xml

Acknowledgements

Thesis Defense v1

By Zachary Sunberg

Thesis Defense v1

  • 454

More from Zachary Sunberg