Safety and Efficiency in Autonomous Vehicles through Online Learning
Zachary Sunberg
Postdoctoral Scholar
University of California
Map with Contributions
Map with Autorotation
Autorotation
"Expert System" Autorotation Controller
Example Controller: Flare
\[\alpha \equiv \frac{KE_{\text{available}} - KE_{\text{flare exit}}}{KE_{\text{flare entry}} - KE_{\text{flare exit}}}\]
\[TTLE = TTLE_{max} \times \alpha\]
\[\ddot{h}_{des} = -\frac{2}{TTI_F^2}h - \frac{2}{TTI_F}\dot{h}\]
Problems with this approach:
- No optimality justification
- Controller must be adjusted by hand to accommodate any changes
- Difficult to communicate about
- Parameters not intuitive
Autorotation Simulation Results
Autonomy
Two Objectives for Autonomy
EFFICIENCY
SAFETY
Minimize resource use
(especially time)
Minimize the risk of harm to oneself and others
Hard Safety: Guaranteeing that there will be no harm
Soft Safety: Reducing the risk of harm
Proper Uncertainty Modeling Can Improve Both
Tweet by Nitin Gupta
29 April 2018
https://twitter.com/nitguptaa/status/990683818825736192
Sadigh, Dorsa, et al. "Information gathering actions over human internal state." Intelligent Robots and Systems (IROS), 2016 IEEE/RSJ International Conference on. IEEE, 2016.
Schmerling, Edward, et al. "Multimodal Probabilistic Model-Based Planning for Human-Robot Interaction." arXiv preprint arXiv:1710.09483 (2017).
Sadigh, Dorsa, et al. "Planning for Autonomous Cars that Leverage Effects on Human Actions." Robotics: Science and Systems. 2016.
Human Behavior Model: IDM and MOBIL
\ddot{x}_\text{IDM} = a \left[ 1 - \left( \frac{\dot{x}}{\dot{x}_0} \right)^{\delta} - \left(\frac{g^*(\dot{x}, \Delta \dot{x})}{g}\right)^2 \right]
g^*(\dot{x}, \Delta \dot{x}) = g_0 + T \dot{x} + \frac{\dot{x}\Delta \dot{x}}{2 \sqrt{a b}}
M. Treiber, et al., “Congested traffic states in empirical observations and microscopic simulations,” Physical Review E, vol. 62, no. 2 (2000).
A. Kesting, et al., “General lane-changing model MOBIL for car-following models,” Transportation Research Record, vol. 1999 (2007).
A. Kesting, et al., "Agents for Traffic Simulation." Multi-Agent Systems: Simulation and Applications. CRC Press (2009).
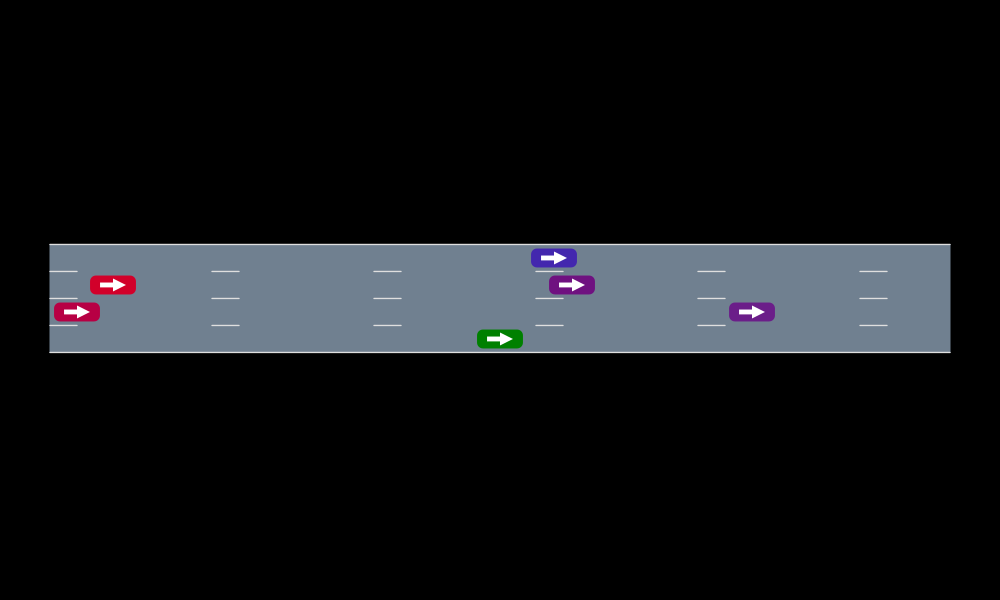
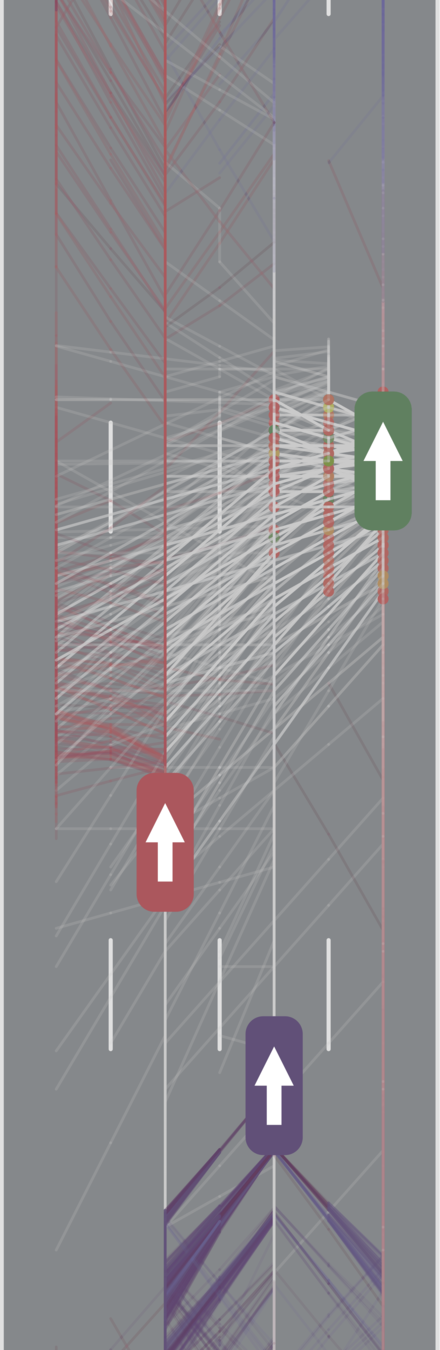
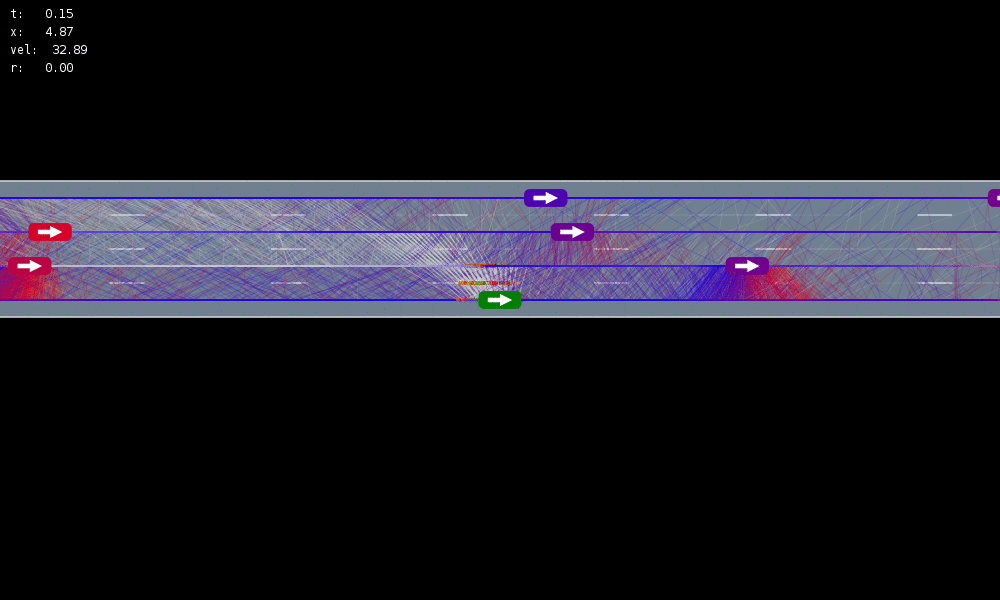
Objective: Safely Change 3 Lanes within 1000m
All drivers normal
Omniscient
Simulation results
All drivers normal
MDP
Omniscient
Mean MPC
QMDP
POMCPOW (Ours)
Simulation results
Monte Carlo Tree Search
Image by Dicksonlaw583 (CC 4.0)
All drivers normal
MDP
Omniscient
Mean MPC
QMDP
POMCPOW (Ours)
Simulation results
All drivers normal
MDP
Omniscient
Mean MPC
QMDP
POMCPOW (Ours)
Simulation results
Conditional Parameter Distributions
Assume normal
Outcome only
Omniscient
Mean MPC
QMDP
POMCPOW
MAP
References
Acknowledgements
The content of my research reflects my opinions and conclusions, and is not necessarily endorsed by my funding organizations.
TODO: HSL PICTURE
Thank You!
Job Talk II
By Zachary Sunberg
