Downloading many-body continuous variable entanglement to qubits

Zhihua Han, Kero Lau

Simon Fraser University

CAP Congress

May 28, 2024

Imagine I have some qubits:

|+\rangle

Qubit cluster state

and now I entangle the edges with the (qubit) CZ gate.

\hat{C}_Z
|+\rangle

Qubit cluster state

\hat{C}_Z = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 &-1 \end{bmatrix}
\begin{aligned} &= |G\rangle \end{aligned}

The quantum state specified by \(G\) is called a qubit cluster state.

\begin{aligned} &= |G\rangle\\ &= \prod_{i, j \in E}\hat{C}_{Z_{ij}} |+\rangle^{\otimes N} \end{aligned}
\hat{C}_Z
|+\rangle

Qubit cluster state

Qubit cluster state

+

Single qubit measurements

Fault tolerant universal quantum computation

(Raussendorf 2001)

Why we need qubit cluster state

Superconducting qubits: 51

Photonic qubits: 14

Trapped ion: 32

Qubit cluster state

Why we need qubit cluster state

Goal: Make many body entanglement in physical qubits

How do we make scalable qubit cluster states?

"Downloading entanglement from a CV cluster state"

Continuous variable (CV) cluster state

Physical qubits

|0, \sigma_p \rangle_p
\hat{C}_Z^\mathrm{CV}

Entanglement Transfer Protocol

How do we make scalable qubit cluster states?

Entanglement Transfer Protocol

Continuous variable (CV) cluster state

Qubit cluster state

|0, \sigma_p \rangle_p
\hat{C}_Z^\mathrm{CV}

Entanglement Transfer Protocol

Now if I have some bosons:

|0, \sigma_p \rangle_p

CV cluster state

Squeezed state

and entangle them with CV CZ gate:

|0, \sigma_p \rangle_p
\hat{C}_Z^\mathrm{CV} = e^{i\hat{q}_1 \hat{q}_2}

CV cluster state

We say it is a CV cluster state.

|0, \sigma_p \rangle_p
\hat{C}_Z^\mathrm{CV} = e^{i\hat{q}_1 \hat{q}_2}
\begin{aligned} &= |G\rangle^\mathrm{CV} \end{aligned}
\begin{aligned} &= |G\rangle^\mathrm{CV}\\ &= \prod_{i, j \in E}\hat{C}_{Z_{ij}}^\mathrm{CV} |0, \sigma_p \rangle_p^{\otimes N} \end{aligned}

CV cluster state

\(\sigma_p\) represents the variance of the squeezed state. 

|0, \sigma_p \rangle_p

When \(\sigma_p \to 0\), the CV cluster state is an ideal CV cluster state.

\(p\)

|0, \sigma_p \rangle_p

Finite vs Ideal CV cluster state

\(\sigma_p\) represents the variance of the squeezed state. 

|0, \sigma_p \rangle_p

When \(\sigma_p \to 0\), the CV cluster state is an ideal CV cluster state.

\(p\)

|0\rangle_p

Finite vs Ideal CV cluster state

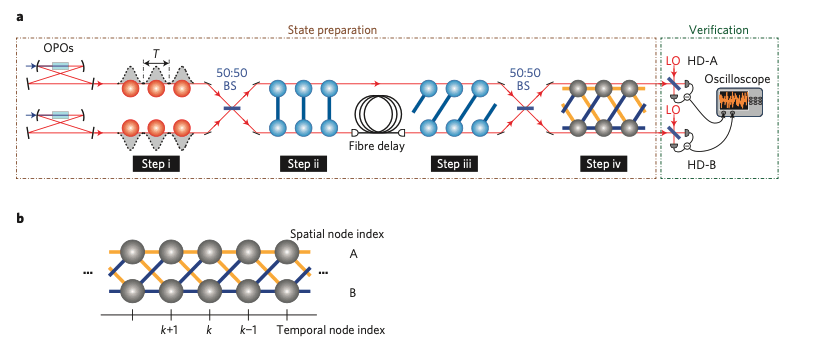
10000 modes! 1D, (Furusawa 2013)

How to make CV cluster state

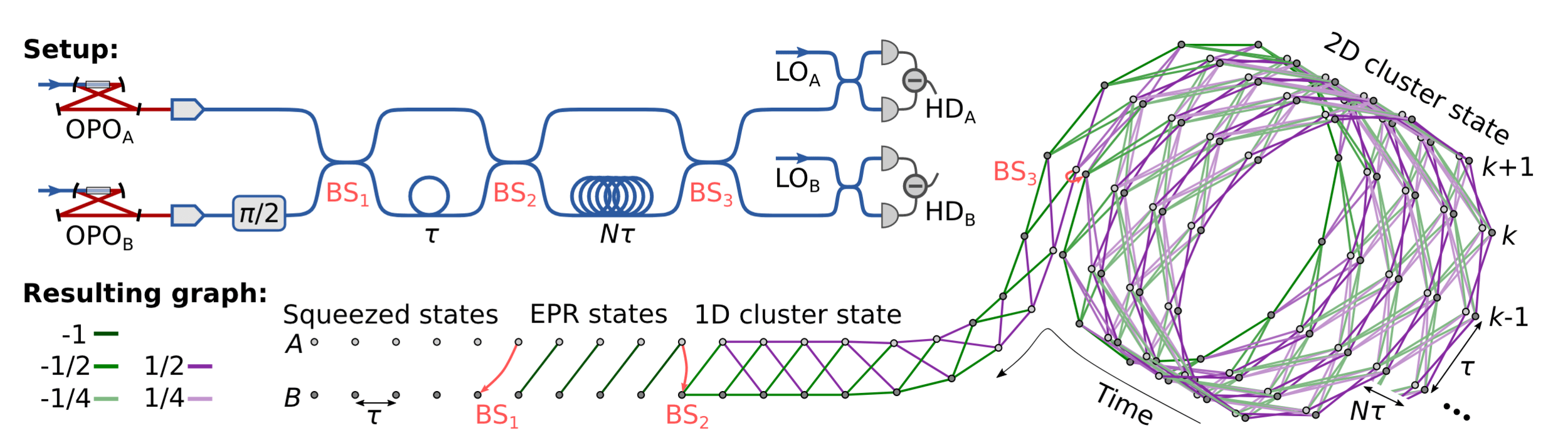
1 million modes, 1D, (Furusawa 2016)

How to make CV cluster state

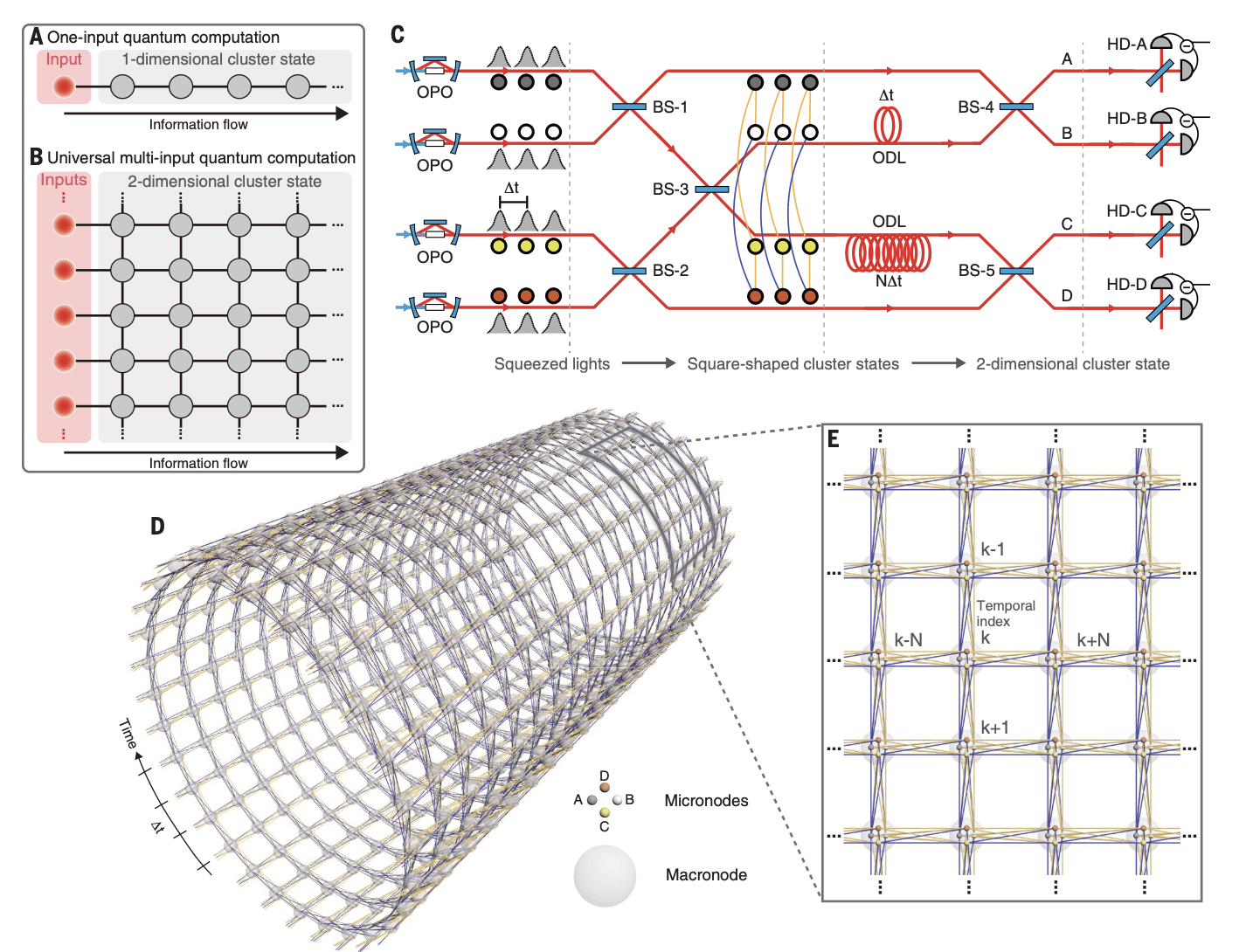
 5x1240 modes, 2D, (Furusawa 2019)

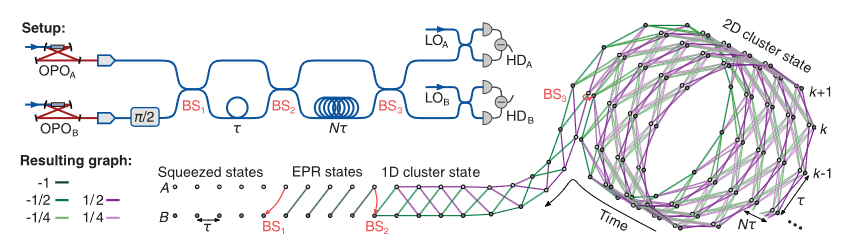
24x1250, 2D (Andersen 2019)

How to make CV cluster state

Ideal CV cluster state

|G\rangle^\mathrm{CV} = \prod_{i, j \in E}\hat{C}_{Z_{ij}}^\mathrm{CV} |0\rangle_p^{\otimes N}
|0\rangle_p
\hat{C}_Z^\mathrm{CV} = e^{i\hat{q}_1 \hat{q}_2}

Qubit cluster state

\begin{aligned} |G\rangle= \prod_{i, j \in E}\hat{C}_{Z_{ij}} |+\rangle^{\otimes N} \end{aligned}
|+\rangle
\hat{C}_Z = \text{diag}(1, 1, 1, -1)

CV vs qubit cluster state

Continuous variable (CV) cluster state

Physical qubits

|0\rangle_p
\hat{C}_Z^\mathrm{CV}

How to perform entanglement transfer?

\hat{C}_Z^\mathrm{CV} = e^{i\hat{q}_1 \hat{q}_2}
\hat{C}_Z = \text{diag}(1, 1, 1, -1)

Entanglement transfer protocol

How to perform entanglement transfer?

Continuous variable (CV) cluster state

Qubit cluster state

|0\rangle_p
\hat{C}_Z
\hat{C}_Z^\mathrm{CV} = e^{i\hat{q}_1 \hat{q}_2}
\hat{C}_Z = \text{diag}(1, 1, 1, -1)

Entanglement transfer protocol

 We need: 

  • A CV cluster state*
  • \(\hat{q}\) quadrature homodyne detection
  • Conditional displacement gate \( \hat{C}_D\)
\hat{C}_D = |0\rangle \langle 0| \hat I + |1\rangle \langle 1| \hat{D}_q({\sqrt{\pi}})

How to perform entanglement transfer?

Entanglement transfer protocol

x

\(\psi (x)\)

\(e^{-ia\hat p}\psi (x)\)

Displacement gate of strength \(a\) shifts the state.

\(a\)

ETP: Displacement Gate

\hat D_q(a) |x\rangle:= |x + a\rangle
\hat D_q(a) |x\rangle:= |x + a\rangle

\(q\)

\(p\)

ETP: Displacement Gate

Displacement gate of strength \(a\) shifts the state.

\(q\)

\(p\)

\(a\)

ETP: Displacement Gate

\hat D_q(a) |x\rangle:= |x + a\rangle

Displacement gate of strength \(a\) shifts the state.

1. Initialize all qubits to \(|+\rangle\).

(These are physical qubits)

|+\rangle

ETP: Overview

Step 2: Get a CV cluster state.

|0\rangle_p
\hat{C}_Z^\mathrm{CV}

ETP: Overview

Step 3. Apply conditional displacement to each pair:

\(\hat{C}_D = |0\rangle \langle 0| \hat I + |1\rangle \langle 1| \hat{D}_q({\sqrt{\pi}})\)

|0\rangle_p
\hat{C}_Z^\mathrm{CV}

ETP: Overview

Step 3. Apply conditional displacement to each pair:

\(\hat{C}_D = |0\rangle \langle 0| \hat I + |1\rangle \langle 1| \hat{D}_q({\sqrt{\pi}})\)

\hat{C}_D

ETP: Overview

Step 4. Measure \(q\) quadrature.

ETP: Overview

You now have a qubit cluster state!

But why does it work?

ETP: Overview

We show there is a hidden qubit cluster  state inside a CV cluster state! 

|0\rangle_p
\hat{C}_Z^\mathrm{CV}

\(q\)

\(q\)

\(q\)

\(q\)

CV cluster state

Qubit cluster inside CV cluster

|0\rangle_\mathrm{GKP} = \sum_{n=-\infty}^{\infty} |2n\sqrt{\pi}\rangle_q

Gottesman-Kitaev-Preskill (GKP state)

\(q\)

\(|2n\sqrt{\pi}\rangle\)

\(0\)

\(2\sqrt \pi\)

\(4\sqrt \pi\)

\(6\sqrt \pi\)

GKP Background

|1\rangle_\mathrm{GKP} = \sum_{n=-\infty}^{\infty} |(2n+1)\sqrt{\pi}\rangle_q

\(q\)

\(|(2n+1)\sqrt{\pi}\rangle\)

\(0\)

\(2\sqrt \pi\)

\(4\sqrt \pi\)

\(6\sqrt \pi\)

\(\sqrt \pi\)

\(3\sqrt \pi\)

\(5\sqrt \pi\)

\hat{X}^{\mathrm{GKP}} = e^{-i \sqrt \pi \hat p} = \hat{D}_q(\sqrt{\pi})

GKP Background

|1\rangle_\mathrm{GKP} = \sum_{n=-\infty}^{\infty} |(2n+1)\sqrt{\pi}\rangle_q

\(q\)

\(|(2n+1)\sqrt{\pi}\rangle\)

\(0\)

\(2\sqrt \pi\)

\(4\sqrt \pi\)

\(6\sqrt \pi\)

\(\sqrt \pi\)

\(3\sqrt \pi\)

\(5\sqrt \pi\)

\(|2n\sqrt{\pi}\rangle\)

|0\rangle_\mathrm{GKP} = \sum_{n=-\infty}^{\infty} |2n\sqrt{\pi}\rangle_q

GKP Background

|+\rangle_\mathrm{GKP} = \sum_{n=-\infty}^{\infty} |n\sqrt{\pi}\rangle_q = \frac{1}{\sqrt{2}}(|0\rangle_\mathrm{GKP} + |1\rangle_\mathrm{GKP})

\(|2n\sqrt{\pi}\rangle\)

\(q\)

\(|(2n+1)\sqrt{\pi}\rangle\)

\(0\)

\(2\sqrt \pi\)

\(4\sqrt \pi\)

\(6\sqrt \pi\)

\(\sqrt \pi\)

\(3\sqrt \pi\)

\(5\sqrt \pi\)

GKP Background

\(p\)

|0\rangle_p

Node of ideal CV cluster

\(q\)

|0\rangle_p

Node of ideal CV cluster

\(q\)

|0\rangle_p
|+\rangle_\mathrm{GKP}

GKP state

Node of ideal CV cluster

\(q\)

|0\rangle_p

\(\mu_q\)

\mu_q \in [-\frac{\sqrt{\pi}}{2}, -\frac{\sqrt{\pi}}{2})
\hat{D}_q(\mu_q)|+\rangle_\mathrm{GKP}

Displaced GKP state

|+_{\mu_q, 0} \rangle_\mathrm{GKP} \equiv \hat{D}_q(\mu_q)|+\rangle_\mathrm{GKP}

(Glancy 2006)

Displaced GKP

\(q\)

|0\rangle_p
|+_{\mu_q, 0} \rangle_\mathrm{GKP} \equiv \hat{D}_q(\mu_q)|+\rangle_\mathrm{GKP}

So if we integrate over \(\mu_q\), we should form an ideal \(|0\rangle_p\) state.

Node of ideal CV cluster is superposition of displaced GKP

Displaced GKP Basis

 

(Glancy 2006)

\(q\)

|0\rangle_p
+
+
+
+
= \int d\mu_q

Node of ideal CV cluster is superposition of displaced GKP

=

Displaced GKP Basis

CV Basis

\(q\)

|0\rangle_p

Edges of ideal CV cluster

\(q\)

|0\rangle_p
\hat{C}_Z^\mathrm{CV}
=

CV Basis

\(q\)

|0\rangle_p

Edges of ideal CV cluster

+
+
+
+
+
+
+
+

\(q\)

|0\rangle_p
\hat{C}_Z^\mathrm{CV}
=
=

\(q\)

|0\rangle_p
+
+
+
+
+
+
+
+

\(q\)

|0\rangle_p
\hat{C}_Z^\mathrm{CV}
= \iint d \mu_{q_1} d \mu_{q_2}
\hat{C}_Z^\mathrm{CV}
\hat{C}_Z^\mathrm{CV}
\hat{C}_Z^\mathrm{CV}

Edges of ideal CV cluster

\hat{C}_Z^\mathrm{CV}

Displaced GKP Basis

CV Basis

\(q\)

|0\rangle_p
+
+
+
+
+
+
+
+

\(q\)

|0\rangle_p
\hat{C}_Z^\mathrm{CV}
\hat{C}_Z^\mathrm{CV}
\hat{C}_Z^\mathrm{CV}
\hat{C}_Z^\mathrm{CV}

Edges of ideal CV cluster

= \iint d \mu_{q_1} d \mu_{q_2}
\hat{C}_Z^\mathrm{CV}
\hat{C}_Z^\mathrm{CV}

\(q\)

|+_{\mu_q, 0} \rangle_\mathrm{GKP}

is a superposition of 

Nodes of a ideal CV cluster state

Displaced GKP states

\hat{C}_Z^\mathrm{CV}
|0\rangle_p

\(q\)

\(q\)

\(q\)

Node of ideal CV cluster is displaced GKP

The edges of the CV cluster state?

GKP CZ gate

|0\rangle_p
\hat{C}_Z^\mathrm{CV}

\(q\)

\(q\)

\(q\)

\(q\)

|+_{\mu_q, 0} \rangle_\mathrm{GKP}

Edge of ideal CV cluster is GKP CZ

\hat{C}_Z^\mathrm{CV} = e^{i\hat{q}_1\hat{q}_2}
|+\rangle_\mathrm{GKP} = \sum_{n=-\infty}^{\infty} |n\sqrt{\pi}\rangle_q
\hat{C}_Z^\mathrm{CV} \ket{++}_{\mathrm{GKP}} = ?

Substitute definition

|+\rangle_\mathrm{GKP} = \sum_{n=-\infty}^{\infty} |n\sqrt{\pi}\rangle_q
e^{i \hat{q}_1 \hat{q}_2} \sum_{n_1, n_2} |n_1\sqrt{\pi}\rangle_q |n_2\sqrt{\pi}\rangle_q = ?
\hat{C}_Z^\mathrm{CV} = e^{i\hat{q}_1\hat{q}_2}

Apply \(\hat q\)

|+\rangle_\mathrm{GKP} = \sum_{n=-\infty}^{\infty} |n\sqrt{\pi}\rangle_q
e^{i \pi n_1 n_2} \sum_{n_1, n_2} |n_1\sqrt{\pi}\rangle_q |n_2\sqrt{\pi}\rangle_q = ?
\hat{C}_Z^\mathrm{CV} = e^{i\hat{q}_1\hat{q}_2}

Expand into even and odd sums

e^{i \pi n_1 n_2} \sum_{n_1, n_2} |n_1\sqrt{\pi}\rangle_q |n_2\sqrt{\pi}\rangle_q = ?

\(n_1\) or \( n_2\) even \(\implies n_1n_2\) is even

\sum_{n_1 \text{ or } n_2 \text{ even }} |n_1\sqrt{\pi}\rangle_q |n_2\sqrt{\pi}\rangle_q
= |00\rangle_\mathrm{GKP} + |01\rangle_\mathrm{GKP} + |10\rangle_\mathrm{GKP}
e^{i \pi n_1 n_2} \sum_{n_1, n_2} |n_1\sqrt{\pi}\rangle_q |n_2\sqrt{\pi}\rangle_q = ?

\(n_1\) and \( n_2\) odd \(\implies n_1n_2\) is odd

-\sum_{n_1 \text{ and } n_2 \text{ odd }} |n_1\sqrt{\pi}\rangle_q |n_2\sqrt{\pi}\rangle_q
= -|11\rangle_\mathrm{GKP}

Edge of ideal CV cluster is logical CZ

= \frac{1}{2}(|00\rangle_\mathrm{GKP} + |01\rangle_\mathrm{GKP} + |10\rangle_\mathrm{GKP} -|11\rangle_\mathrm{GKP})
\hat{C}_Z^\mathrm{CV} \ket{++}_{\mathrm{GKP}}

Logical qubit CZ gate on GKP states!

= \sum_{n_1, n_2}e^{i \pi n_1 n_2} |n_1\sqrt{\pi}\rangle_q |n_2\sqrt{\pi}\rangle_q
\equiv \hat{C}_Z^\mathrm{GKP} \ket{++}_{\mathrm{GKP}}
\hat{C}_Z^\mathrm{CV}

Edge of ideal CV cluster is logical CZ

=
\hat{C}_Z^\mathrm{CV}
\hat{C}_Z^\mathrm{GKP}

What about CV CZ on a displaced GKP state?

\hat{C}_Z^\mathrm{CV} \ket{++_{\pmb{\mu}}}_{\mathrm{GKP}} = \,?

Edge of ideal CV cluster is logical CZ

\begin{bmatrix} \mu_{q_1} \\ \mu_{q_2} \\ \mu_{p_1} + \mu_{q_2} \\ \mu_{p_2} + \mu_{q_1} \\ \end{bmatrix}
\begin{bmatrix} \mu_{q_1} \\ \mu_{q_2} \\ \mu_{p_1}\\ \mu_{p_2}\\ \end{bmatrix}
\hat{C}_Z^\mathrm{GKP}
=
\hat{C}_Z^\mathrm{CV}
\hat{C}_Z^\mathrm{CV} \ket{++_{\pmb{\mu}}}_{\mathrm{GKP}} = \hat{C}_Z^\mathrm{GKP} \ket{++_{\pmb{\mu}'}}_{\mathrm{GKP}}

Edge of ideal CV cluster is logical CZ

\hat{C}_Z^\mathrm{CV} \ket{++_{\pmb{\mu}}}_{\mathrm{GKP}} = \hat{C}_Z^\mathrm{GKP} \ket{++_{\pmb{\mu}'}}_{\mathrm{GKP}}
\hat{C}_Z^\mathrm{GKP}
=
\equiv \hat{C}_Z^\mathrm{GKP} \ket{++}_{\mathrm{GKP}}
\hat{C}_Z^\mathrm{CV}
\begin{bmatrix} \mu_{q_1} \\ \mu_{q_2} \\ 0 + \mu_{q_2} \\ 0 + \mu_{q_1} \\ \end{bmatrix}
\begin{bmatrix} \mu_{q_1} \\ \mu_{q_2} \\ 0\\ 0\\ \end{bmatrix}

Ideal CV cluster:

\(\mu_p = 0\)

|0\rangle_p
\hat{C}_Z^\mathrm{CV}

Displaced GKP cluster inside a CV cluster

|0\rangle_p
\hat{C}_Z^\mathrm{CV}
= \int \ldots
+
+

Displaced GKP cluster inside a CV cluster

= \int \ldots
q = (2n+L)\sqrt\pi + \mu_q
|0\rangle_p
\hat{C}_Z^\mathrm{CV}
+
+

Homodyne detection collapses the GKP cluster

|0\rangle_p
\hat{C}_Z^\mathrm{CV}
\hat{C}_Z^{\mathrm{GKP}}

Displaced GKP cluster state inside a CV cluster... How to get the entanglement out?

Displaced GKP cluster inside a CV cluster

= \int \ldots
|+_{\mu_q, 0} \rangle_\mathrm{GKP}
\hat{C}_Z^{\mathrm{GKP}}

Interpret the GKP cluster as a qubit cluster.

We perform qubit-qubit quantum teleportation.

Displaced GKP cluster to qubit cluster

\hat{C}_Z^{\mathrm{GKP}} = \text{diag}(1, 1, 1, -1)

Interpret the GKP cluster as a qubit cluster.

We perform qubit-qubit quantum teleportation.

\hat{C}_Z = \text{diag}(1, 1, 1, -1)
\ket+

Displaced GKP cluster to qubit cluster

qubit 

qubit 

qubit 

One bit teleportation

qubit 

qubit 

qubit 

One bit teleportation

qubit 

GKP (logical qubit)

qubit 

teleportation by products

qubit 

qubit 

qubit 

GKP-qubit one bit teleportation

|0\rangle_\mathrm{GKP} = \sum_{n=-\infty}^{\infty} |2n\sqrt{\pi}\rangle_q

Gottesman-Kitaev-Preskill (GKP state)

\(q\)

\(|2n\sqrt{\pi}\rangle\)

\(0\)

\(2\sqrt \pi\)

\(4\sqrt \pi\)

\(6\sqrt \pi\)

GKP-qubit one bit teleportation: X gate

|1\rangle_\mathrm{GKP} = \sum_{n=-\infty}^{\infty} |(2n+1)\sqrt{\pi}\rangle_q

\(q\)

\(|(2n+1)\sqrt{\pi}\rangle\)

\(0\)

\(2\sqrt \pi\)

\(4\sqrt \pi\)

\(6\sqrt \pi\)

\(\sqrt \pi\)

\(3\sqrt \pi\)

\(5\sqrt \pi\)

\hat{X}^{\mathrm{GKP}} = e^{-i \sqrt \pi \hat p} = \hat{D}_q(\sqrt{\pi})

GKP-qubit one bit teleportation: X gate

|0\rangle_\mathrm{GKP} = \sum_{n=-\infty}^{\infty} |2n\sqrt{\pi}\rangle_q

Gottesman-Kitaev-Preskill (GKP state)

\(q\)

\(|2n\sqrt{\pi}\rangle\)

\(0\)

\(2\sqrt \pi\)

\(4\sqrt \pi\)

\(6\sqrt \pi\)

GKP-qubit one bit teleportation: \(\mu_q, \mu_p\)

|1\rangle_\mathrm{GKP} = \sum_{n=-\infty}^{\infty} |(2n+1)\sqrt{\pi}\rangle_q

\(q\)

\(0\)

\(2\sqrt \pi\)

\(4\sqrt \pi\)

\(6\sqrt \pi\)

\(\sqrt \pi\)

\(3\sqrt \pi\)

\(5\sqrt \pi\)

\(|2n\sqrt{\pi}+\mu_q\rangle\)

\(\mu_q\): Rotational X gate

\(\mu_p\): Rotational Z gate

\(\mu_q, \mu_p\) as rotational X, Z

qubit 

GKP (logical qubit)

teleportation by products

qubit 

qubit 

qubit 

GKP-qubit one bit teleportation

qubit 

GKP (logical qubit)

qubit 

qubit 

qubit 

qubit 

GKP-qubit one bit teleportation: X gate

GKP X gate

qubit 

GKP (logical qubit)

qubit 

qubit 

qubit 

qubit 

GKP-qubit one bit teleportation: \(\mu_p\)

displaced GKP interpreted as rotated qubit

qubit 

GKP (logical qubit)

qubit 

qubit 

qubit 

qubit 

q = (2n+L)\sqrt\pi + \mu_q

GKP-qubit one bit teleportation: \(\mu_q\)

teleport based on

logical value = {0, 1} of GKP

qubit 

GKP (logical qubit)

qubit 

q = (2n+L)\sqrt\pi + \mu_q

Homodyne detection roles:

1. Collapsing the superposition into some GKP cluster

2. ​Quantum teleportation

Entanglement transfer protocol: Recap

1. Initialize all qubits to \(|+\rangle\).

|+\rangle

Entanglement transfer protocol: Recap

|+\rangle
|0\rangle_p
\hat{C}_Z^\mathrm{CV}

2. Create a CV cluster state.

Entanglement transfer protocol: Recap

|+\rangle
|0\rangle_p

Step 3. Apply conditional displacement to each pair:

\(\hat{C}_D = |0\rangle \langle 0| \hat I + |1\rangle \langle 1| \hat{D}_q({\sqrt{\pi}})\)

Entanglement transfer protocol: Recap

|+\rangle
|0\rangle_p
\hat{C}_D

Step 3. Apply conditional displacement to each pair:

\(\hat{C}_D = |0\rangle \langle 0| \hat I + |1\rangle \langle 1| \hat{D}_q({\sqrt{\pi}})\)

Entanglement transfer protocol: Recap

Step 4. Measure the \(q\) quadrature.

|+\rangle
|0\rangle_p

Entanglement transfer protocol: Recap

|+\rangle

Step 5. Correct by products.

Entanglement transfer protocol: Recap

\hat{C}_Z\ket{++}

Entanglement transfer protocol: Loss

1. Ideal CV cluster \(\to\) perfect qubit cluster

2. No reference to GKP states in the protocol

3. Generalizes to arbitrary graph \(G\)

Detector Loss

Channel Loss

Finite squeezing

Entanglement transfer protocol: Loss

Detector Loss

Channel Loss

Finite squeezing

Entanglement transfer protocol: Loss

Detector Loss

Channel Loss

Finite squeezing

Entanglement transfer protocol: Loss

non trivial math ✨

Equivalent circuit model

Squeezed thermal state

loss reduces entanglement transferred

Entanglement transfer protocol: Loss

Finite squeezing:

\(p\)

|0, \sigma_p \rangle_p

Loss: Finite Squeezing

\(q\)

|0, \sigma_p \rangle_p

Finite squeezing:

Loss: Finite Squeezing

\(q\)

\hat{D}_q(\sqrt{\pi})|0, \sigma_p \rangle_p \ket{1}^{\mathrm{Qubit}}

After conditional displacement:

|0, \sigma_p \rangle_p \ket{0}^{\mathrm{Qubit}}

Loss: Finite Squeezing

\(q\)

\hat{D}_q(\sqrt{\pi})|0, \sigma_p \rangle_p \ket{1}^{\mathrm{Qubit}}

Now, the probability of measuring \(q\):

|0, \sigma_p \rangle_p \ket{0}^{\mathrm{Qubit}}

Loss: Finite Squeezing

\(q\)

The displaced GKP state after measuring \(q\):

Loss: Finite Squeezing

\(q\)

The displaced GKP state after measuring \(q\):

Loss: Finite Squeezing

\(q\)

The displaced GKP state after measuring \(q\):

\ket{0} + \, \, \ket 1

Amplitude imbalance error

The qubit is:

Loss: Finite Squeezing

\ket{0} + \, \, \ket 1

Amplitude imbalance error

The qubit is:

We can correct the qubit by performing weak measurement POVMs \(M_0, M_1\). 

Failure:

\ket{1}
\ket{0} + \, \, \ket 1

Success:

Loss: Finite Squeezing

\ket{0} + \, \, \ket 1

Amplitude imbalance error

The qubit is:

We can correct the qubit by performing weak measurement POVMs \(M_0, M_1\).

Failure: \(p\)

\ket{1}
\ket{0} + \, \, \ket 1

Success: \(1-p\)

\hat M_0
\hat M_1

Loss: Finite Squeezing

Finitely squeezed CV cluster state

Loss: Finite Squeezing

Loss: Finite Squeezing

Amplitude imbalance error!

After weak measurement:

Loss: Finite Squeezing

Failure: \(p\)

Can convert initial squeezing error to deletion error!

Loss: Finite Squeezing

Loss: Finite Squeezing

Failure: \(p\)

(Stace 2009)

(Barrett and Stace 2010)

Site 1

Site 2

Site 3

Loss: Finite Squeezing

Loss: Finite Squeezing

After weak measurement:

Loss: Finite Squeezing

Dual rail encoding (n=2)

Loss: Finite Squeezing

In order to break entanglement between site 1 and 3 both qubits has to be deleted.

Dual rail encoding (n=2)

Loss: Finite Squeezing

Deletion probability of a site: \(p^n\)

What happens to the qubit if you send in a squeezed thermal state?

\(q\)

\(p\)

\rho^{\mathrm{thermal}}
= \rho

\(q\)

\(p\)

|0, \sigma_p \rangle_p
\hat{D}_p(p_0)

Squeezed thermal state

Loss: Channel and detector loss

What happens to the qubit if you send in a squeezed thermal state?

\(q\)

\(p\)

\rho^{\mathrm{thermal}}
= \rho

\(q\)

\(p\)

|0, \sigma_p \rangle_p
\hat{D}_p(p_0)

Mixture of squeezed states

Squeezed thermal state

=

Loss: Channel and detector loss

What happens to the qubit if you send in a squeezed thermal state?

\(q\)

\(p\)

\rho^{\mathrm{thermal}}

\(q\)

\(p\)

|0, \sigma_p \rangle_p
\hat{D}_p(p_0)

Loss: Channel and detector loss

\rho

What happens to the qubit if you send in a squeezed thermal state?

\(q\)

\(p\)

\rho^{\mathrm{thermal}}

\(q\)

\(p\)

|0, \sigma_p \rangle_p
\hat{D}_p(p_0)

Qubit dephases

Loss: Channel and detector loss

\rho

Suppose \(\hat{C}_D\) is 3 times weaker

Weak conditional displacement

Suppose \(\hat{C}_D\) is 3 times weaker

Weak conditional displacement

Suppose \(\hat{C}_D\) is 3 times weaker

Weak conditional displacement

Weak conditional displacement can be cancelled out by performing entanglement transfer more times.

Suppose \(\hat{C}_D\) is 3 times weaker

Weak conditional displacement

Only one round of weak measurement correction.

Suppose \(\hat{C}_D\) is 3 times weaker

Weak conditional displacement

Possible implementations: Superconducting qubits

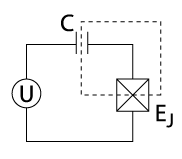
Transmon

CV cluster: Frequency comb in microwave resonator

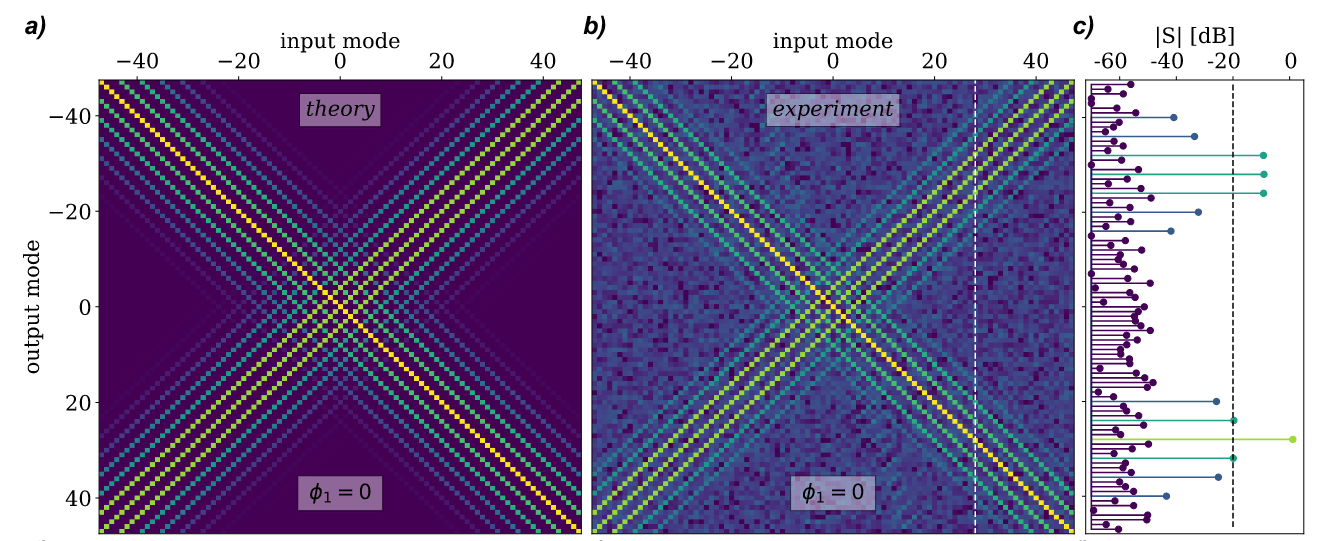
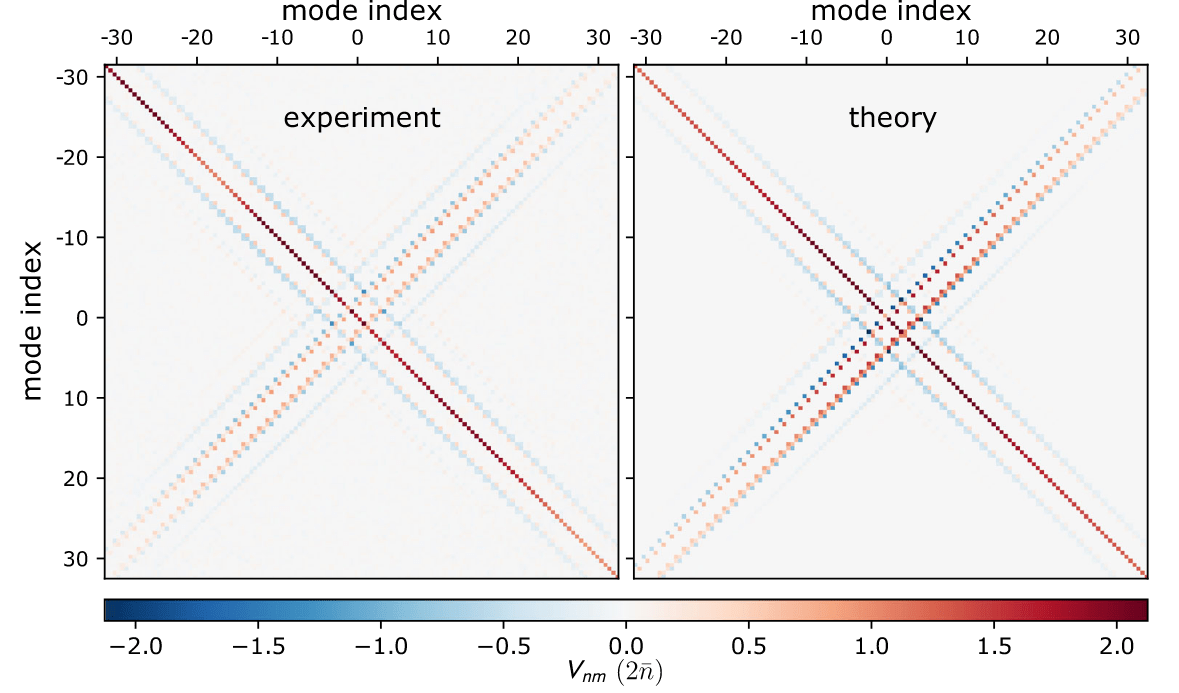
64 correlated modes

(Jolin 2023)

95 correlated modes

(Hernández 2024)

Possible implementations: Superconducting qubits

Transmon

CV cluster: Frequency comb in microwave resonator

Conditional displacement:

ECD gate (A. Eickbusch 2018)

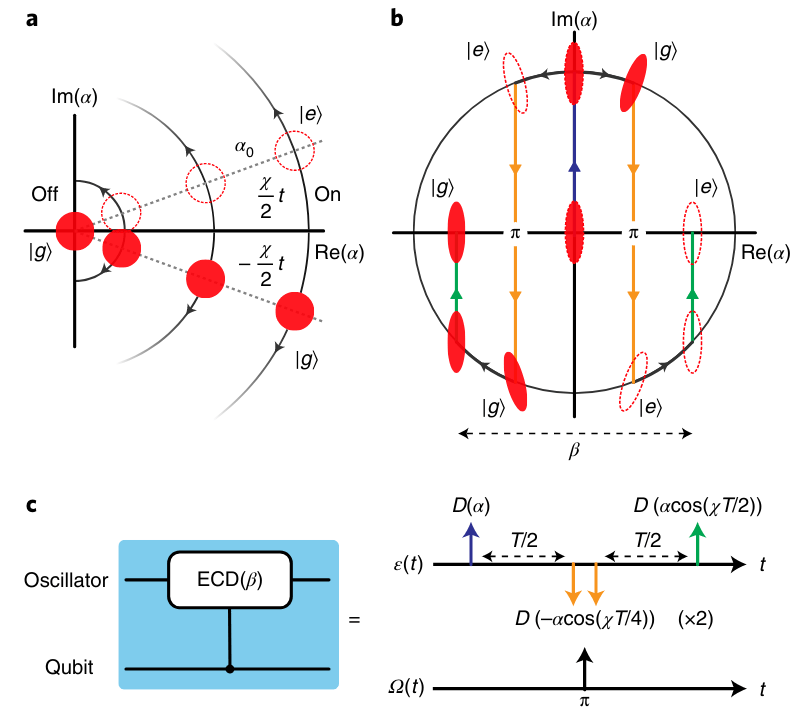
Possible implementations: Superconducting qubits

Transmon

CV cluster: Frequency comb in microwave resonator

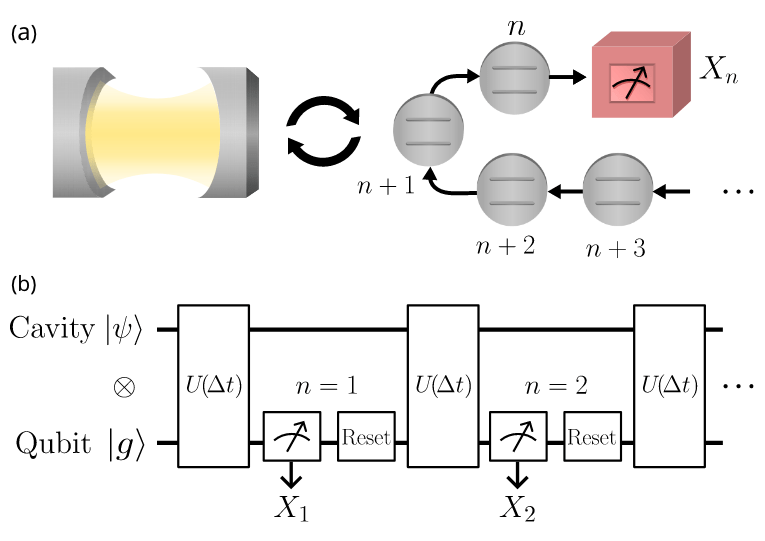
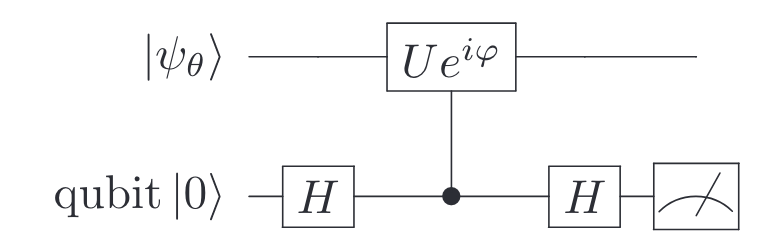
Qubitdyne detection (Strandberg 2023)

Quantum Phase Estimation (Terhal and Weigand 2016)

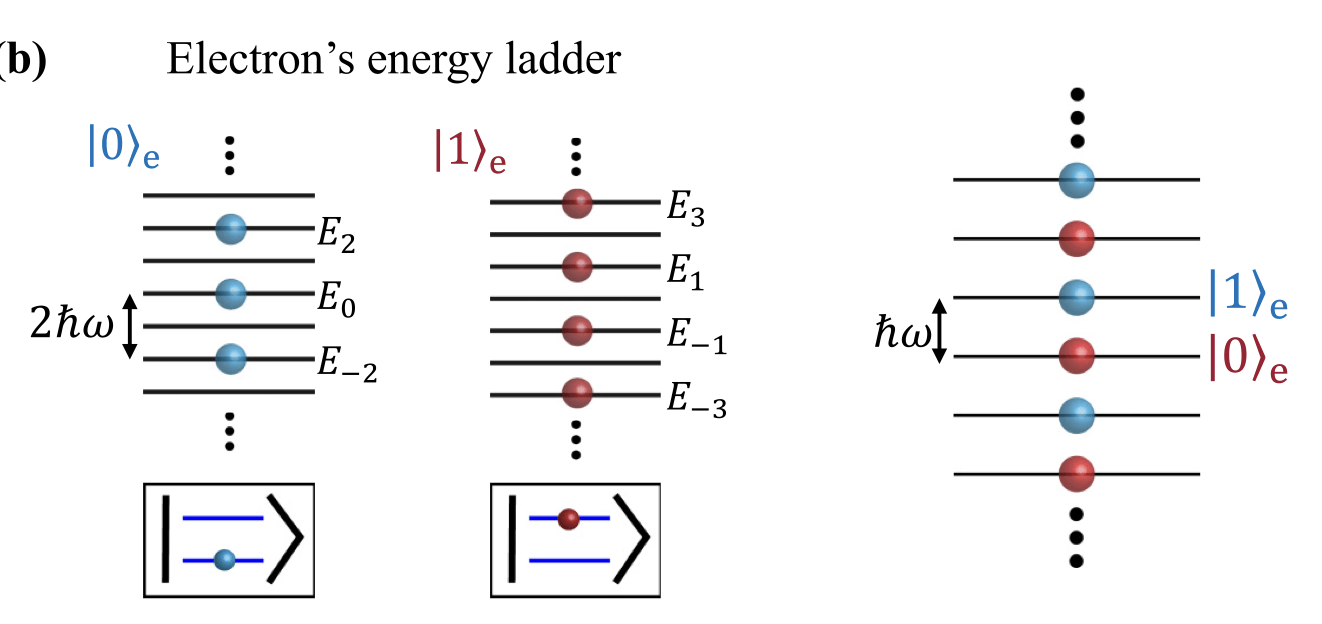
Possible implementations: Free electron qubits

Free electron qubits

(Reinhardt 2021, Baranes 2024)

CV cluster: Furusawa protocol

Homodyne detection

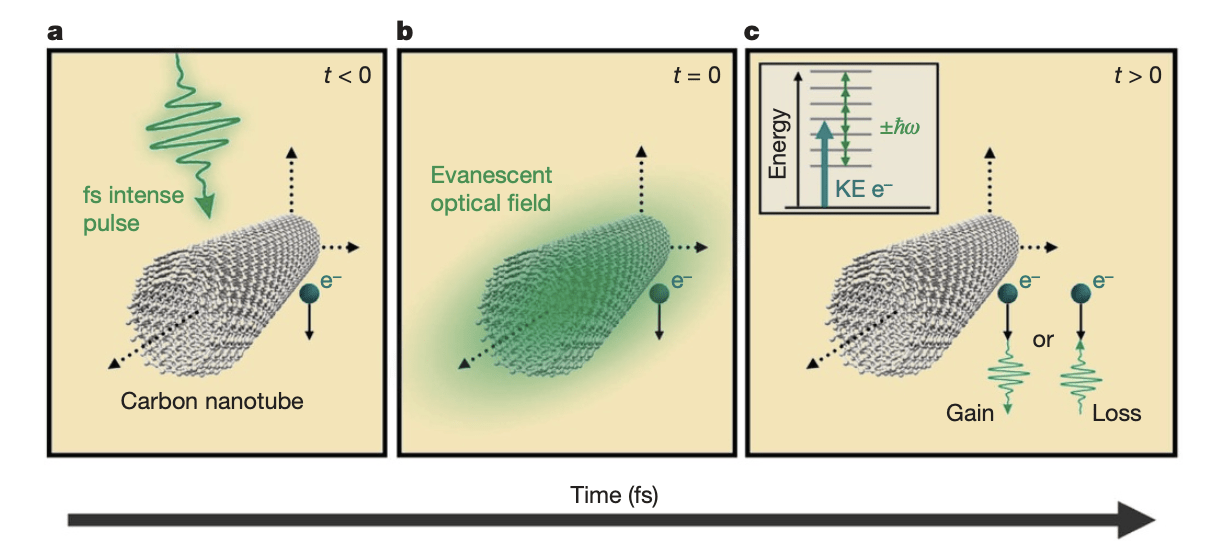
CD gate: Photon-induced near-field electron microscopy (PINEM) 

(Barwick 2009)

Superconducting qubit + microwave cavity Free electron qubits
CV cluster state Frequency comb in cavity  Optics 
Conditional displacement Echoed conditional displacement gate (ECD gate) PINEM (photon-induced near field electron microscopy)
Homodyne detection Quantum phase estimation
Qubitdyne detection		 Homodyne detection
Qubit Transmon Free electrons

Possible implementations: Summary

Downloading many-body continuous variable entanglement to qubits

  • We can make many body entanglement in qubits!
  • Entanglement transfer from CV cluster state to qubit cluster state is possible
  • Quality of the qubit cluster state depends on initial CV cluster
  • Weak measurement / qubit deletion protocol can reduce requirements
  • ​6dB squeezing for robust quantum memory
  • 12dB squeezing for fault tolerant quantum computing
  • No generation of GKP states is needed
  • arXiV in progress
  • This research was sponsored by the QuantumBC CREATE Program.

Zhihua Han: zhi_han@sfu.ca

References

[1] W. Asavanant et al., Generation of Time-Domain-Multiplexed Two-Dimensional Cluster State, Science 366, 373 (2019).

[2] S. Takeda and A. Furusawa, Toward Large-Scale Fault-Tolerant Universal Photonic Quantum Computing, APL Photonics 4, 060902 (2019).

[3] J. Yoshikawa, S. Yokoyama, T. Kaji, C. Sornphiphatphong, Y. Shiozawa, K. Makino, and A. Furusawa, Invited Article: Generation of One-Million-Mode Continuous-Variable Cluster State by Unlimited Time-Domain Multiplexing, APL Photonics 1, 060801 (2016).

[4] Nicolas C. Menicucci, Peter van Loock, Mile Gu, Christian Weedbrook, Timothy C. Ralph, and Michael A. Nielsen, Universal Quantum Computation with Continuous-Variable Cluster States, Phys. Rev. Lett. 97, 110501 (2006).

[5] Shota Yokoyama et al., Ultra-large-scale continuous-variable cluster states multiplexed in the time domain, Nat. Photonics 7, 5 (2013).

[6] J. Yoshikawa, S. Yokoyama, T. Kaji, C. Sornphiphatphong, Y. Shiozawa, K. Makino, and A. Furusawa, Invited Article: Generation of One-Million-Mode Continuous-Variable Cluster State by Unlimited Time-Domain Multiplexing, APL Photonics 1, 060801 (2016).

[7] T. Monz, P. Schindler, J. T. Barreiro, M. Chwalla, D. Nigg, W. A. Coish, M. Harlander, W. Hänsel, M. Hennrich, and R. Blatt, 14-Qubit Entanglement: Creation and Coherence, Phys. Rev. Lett. 106, 130506 (2011).

[8] C. Song et al., Generation of Multicomponent Atomic Schrödinger Cat States of up to 20 Qubits, Science 365, 574 (2019).

[9] X.-L. Wang et al., Experimental Ten-Photon Entanglement, Phys. Rev. Lett. 117, 210502 (2016).

[10] R. Raussendorf, D. E. Browne, and H. J. Briegel, Measurement-Based Quantum Computation with Cluster States, Phys. Rev. A 68, 022312 (2003).

 

References

[11] D. Gottesman, A. Kitaev, and J. Preskill, Encoding a Qubit in an Oscillator, Phys. Rev. A 64, 012310 (2001).

[12] J. E. Bourassa et al., Blueprint for a Scalable Photonic Fault-Tolerant Quantum Computer, Quantum 5, 392 (2021).

[13] S. Glancy and E. Knill, Error Analysis for Encoding a Qubit in an Oscillator, Phys. Rev. A 73, 012325 (2006).

[14] A. Botero and B. Reznik, Modewise Entanglement of Gaussian States, Phys. Rev. A 67, 052311 (2003).

[15] C. Weedbrook, S. Pirandola, R. Garcia-Patron, N. J. Cerf, T. C. Ralph, J. H. Shapiro, and S. Lloyd, Gaussian Quantum Information, Rev. Mod. Phys. 84, 621 (2012).

[16] S. L. Braunstein and P. van Loock, Quantum Information with Continuous Variables, Quantum Information with Continuous Variables 77, 65 (2005).

[17] S. Takeda and A. Furusawa, Toward Large-Scale Fault-Tolerant Universal Photonic Quantum Computing, APL Photonics 4, 060902 (2019).

[18] R. Raussendorf, D. E. Browne, and H. J. Briegel, Measurement-Based Quantum Computation with Cluster States, Phys. Rev. A 68, 022312 (2003).

[19] M. V. Larsen, X. Guo, C. R. Breum, J. S. Neergaard-Nielsen, and U. L. Andersen, Deterministic Generation of a Two-Dimensional Cluster State, Science 366, 369 (2019).

[20] B. M. Terhal and D. Weigand, Encoding a Qubit into a Cavity Mode in Circuit QED Using Phase Estimation, Phys. Rev. A 93, 012315 (2016).

References

[21] O. Reinhardt, C. Mechel, M. Lynch, and I. Kaminer, Free-Electron Qubits, Annalen Der Physik 533, 2000254 (2021).

[22] G. Baranes, S. Even-Haim, R. Ruimy, A. Gorlach, R. Dahan, A. A. Diringer, S. Hacohen-Gourgy, and I. Kaminer, Free-Electron Interactions with Photonic GKP States: Universal Control and Quantum Error Correction, Phys. Rev. Res. 5, 043271 (2023).

[23] R. Dahan, G. Baranes, A. Gorlach, R. Ruimy, N. Rivera, and I. Kaminer, Creation of Optical Cat and GKP States Using Shaped Free Electrons, Phys. Rev. X 13, 031001 (2023).

[24] B. Hacker, S. Welte, S. Daiss, A. Shaukat, S. Ritter, L. Li, and G. Rempe, Deterministic Creation of Entangled Atom–Light Schrödinger-Cat States, Nature Photon 13, 110 (2019).

[25] I. Strandberg, A. Eriksson, B. Royer, M. Kervinen, and S. Gasparinetti, Digital Homodyne and Heterodyne Detection for Stationary Bosonic Modes, arXiv:2312.14720.

[26] A. Eickbusch, V. Sivak, A. Z. Ding, S. S. Elder, S. R. Jha, J. Venkatraman, B. Royer, S. M. Girvin, R. J. Schoelkopf, and M. H. Devoret, Fast Universal Control of an Oscillator with Weak Dispersive Coupling to a Qubit, Nat. Phys. 18, 1464 (2022).

[27] B. Wang and L.-M. Duan, Engineering Superpositions of Coherent States in Coherent Optical Pulses through Cavity-Assisted Interaction, Phys. Rev. A 72, 022320 (2005).

[28] S. Kono, K. Koshino, Y. Tabuchi, A. Noguchi, and Y. Nakamura, Quantum Non-Demolition Detection of an Itinerant Microwave Photon, Nature Phys 14, 546 (2018).

[29] J. Hastrup and U. L. Andersen, Protocol for Generating Optical Gottesman-Kitaev-Preskill States with Cavity QED, Phys. Rev. Lett. 128, 170503 (2022).

[30] A. Reiserer, S. Ritter, and G. Rempe, Nondestructive Detection of an Optical Photon, Science 342, 1349 (2013).

[31] J. C. R. Hernández, F. Lingua, S. W. Jolin, and D. B. Haviland, Control of Multi-Modal Scattering in a Microwave Frequency Comb, arXiv:2402.09068.

[32] S. W. Jolin, G. Andersson, J. C. R. Hernández, I. Strandberg, F. Quijandría, J. Aumentado, R. Borgani, M. O. Tholén, and D. B. Haviland, Multipartite Entanglement in a Microwave Frequency Comb, Phys. Rev. Lett. 130, 120601 (2023).