Mapping graph state orbits under local complementation
Presented by Zhi Han
Simon Fraser University & Aalto University
slides.com/zhihan/lc



Overview
- Rubik's cube
- Group Theory and Cayley graphs
- Local complementation forms a group
- Graph states
- Local complementation

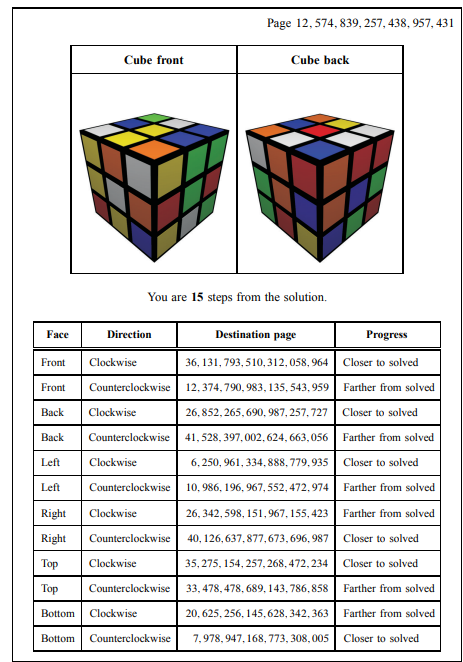
43 quintillion permutations!



Speedcubers
World Cube Association




http://cube20.org/qtm/




This is in the paper

Is this an efficient way of solving the cube?
How can we use group theory to speed up solving the cube, if we don't compute every state/action?

How do speedcubers actually solve the cube?
https://jperm.net/3x3/cfop



How to find God's algorithm?
CFOP discovered using group theory and brute force?

brute force?
Group theory
Example of Groups


Ref. [2]


Ref. [2]



Cayley graph. A cayley graph always defines a group.
Isomorphic
Ref. [2]
Can always go from a Cayley diagram (states) to a diagram of actions.


Can do algebra, etc...
Ref. [2]

Can do algebra, etc...

Mulitplication Table
Ref. [2]
Definition of a Group
-
Closure: Any two composed actions must belong to the group.
-
Identity: There exists an action that does nothing.
-
Inverses: The inverse action must be part of the group.
-
Associativity: Rearranging the parentheses when composing actions does not affect the result.
-
Closure: \(g_1 g_2 \in G \quad \forall g_1 ,g_2 \in G\)
-
Identity: \( e \in G \quad eg = ge = g\)
-
Inverses: \(g \in G \implies g^{-1} \in G\)
-
Associativity: \(( g_1 g_2) g_3 = g_1 (g_2 g_3)\)


Ref. [2]

Ref. [2]

Ref. [2]
Group theory summary
- Group specified by a Cayley diagram.
- Groups \(G\) are the actions that act on a set \(S\) states.
- Cayley diagrams are not very scalable.
- Bonus slides below: Orbit - Stabilizer Theorem


Orbit stabilizer theorem

The actual paper
The actual paper
State \(S\): Graph states
Group \(G\): Local complementation on qubit \(i\)


A graph state is specified by a graph \(G = (V, E)\). \(V\) is the qubit initalized to \(|+\rangle\) and for each edge apply the \(C_Z \) operation.
\(|+\rangle\)
\(|+\rangle\)
\(|+\rangle\)
\(|+\rangle\)
Graph states
Cluster states

Image [1]
Why do we care?
https://pennylane.ai/qml/demos/tutorial_mbqc.html

Graph state
Measuring graph state
Constructing graph state
entanglement in graph states are considered a resource in measurement based quantum computers
Why do we care?

https://pennylane.ai/qml/demos/tutorial_mbqc.html
entanglement in graph states are considered a resource in measurement based quantum computers
knowing how to transform a graph state without consuming entanglement is very useful
knowing how to transform a graph state without consuming entanglement is very useful
entanglement in graph states are considered a resource in measurement based quantum computers
Local complementation doesn't change the entanglement
Why do we care?

Local complementation doesn't change the entanglement
Why do we care?
Local complementation doesn't change the entanglement
- Classical Communication (CC)
- Local Operations (LO)
LOCC = entanglement invariant operations

knowing how to transform a graph state without consuming entanglement is very useful
entanglement in graph states are considered a resource in measurement based quantum computers
Local complementation doesn't change the entanglement
What other graph state operations doesn't change entanglement?
-
LC = Local complementation
-
LPM = (Local Pauli) measurements
-
CC = Classical communication



What other graph state operations doesn't change entanglement?
LPM = (Local Pauli) measurements
Why do we care?
Image [1]
- LC = Local complementation
- LPM = (Local Pauli) measurements
- CC = Classical communication




Vertex minor problem: NP-complete

Local complementation


That is, in the neighbourhood of α, it removes edges if they are present, and adds any edges are missing (see Fig. 1a).

\(L_3\)


\(L_3\)
\(C_3\)
\(L_3\): Full Cayley graph for class 3
\(C_3\): \(L_3\) under isomorphism graphs


\(L_3\)
\(C_3\)

We denote orbits \(C_i\) when isomorphic graphs are considered equal (unlabelled graph states), and \(L_i\) otherwise (labelled graph states).
\(L_4\)
\(C_4\)

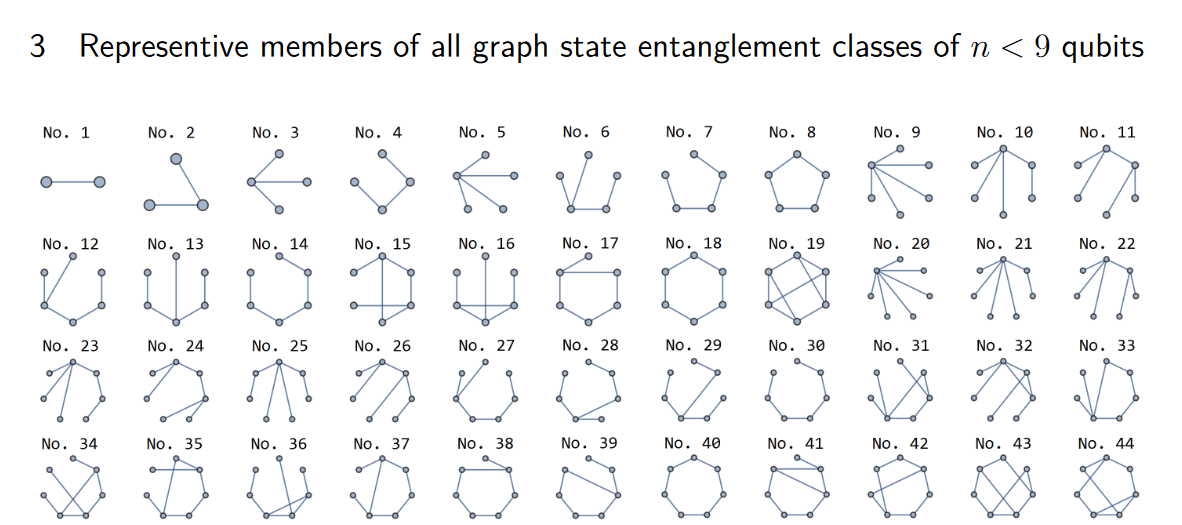
[3]. They only compute up to entanglement class 148, or 8 qubits. Exact scaling is not known but seems doubly exponential

Cayley graph of \(L_{10}\)
\(L_{10}\)

Cayley graph of \(L_{10}\)
Adjacency Matrix of \(L_{10}\).

Note that number of group actions doesn't equal the set

Cayley graph of \(L_{10}\)
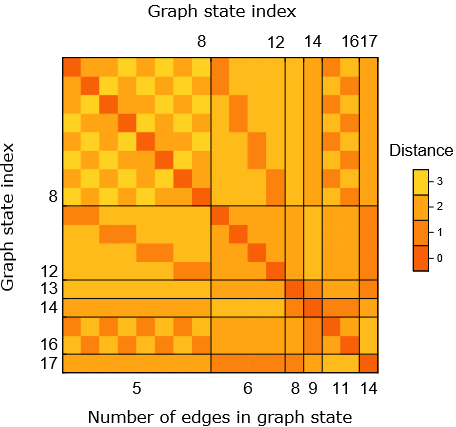
Distance Matrix of \(L_{10}\)

Computing the correlations for each orbit
\(E_S\) Schmidt measure
\(d\): distance between graph states in the orbit
\(\chi\) chromatic index
rwd: rank index
|e|: minimum number edges

\(E_S\) Schmidt measure
\(d\): distance between graph states in the orbit
\(\chi\) chromatic index
rwd: rank index
|e|: minimum number edges
Summary
- Local complementation is a operation that preserves entanglement.
- Knowing the Cayley graph for Local Complementation on graph states might help us develop a God's algorithm for error correcting quantum states.
- This paper computes the Cayley graphs for up to 9 qubits.

[1] J. C. Adcock, S. Morley-Short, A. Dahlberg, and J. W. Silverstone, Mapping Graph State Orbits under Local Complementation, Quantum 4, 305 (2020).
[2] http://www.math.clemson.edu/~macaule/classes/m20_math4120/index.html
[3] Cabello, A., Danielsen, L. E., Lopez-Tarrida, A. J. & Portillo, J. R. Optimal preparation of graph states. Physical Review A 83, 042314 (2011).
[4] https://pennylane.ai/qml/demos/tutorial_mbqc.html
References
[1] https://www.semanticscholar.org/paper/Quantum-Computing-with-Cluster-States-Gelo-Tabia/9a42a72224e9199298e0cd37eb11739f216c86ad